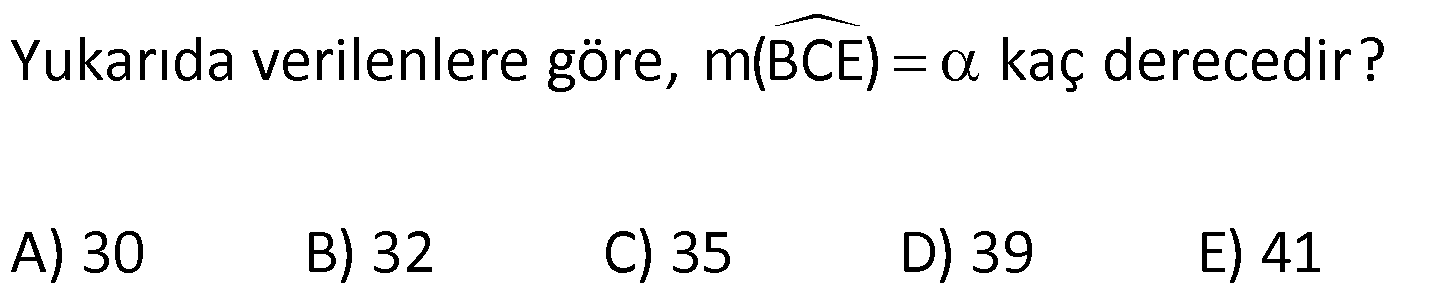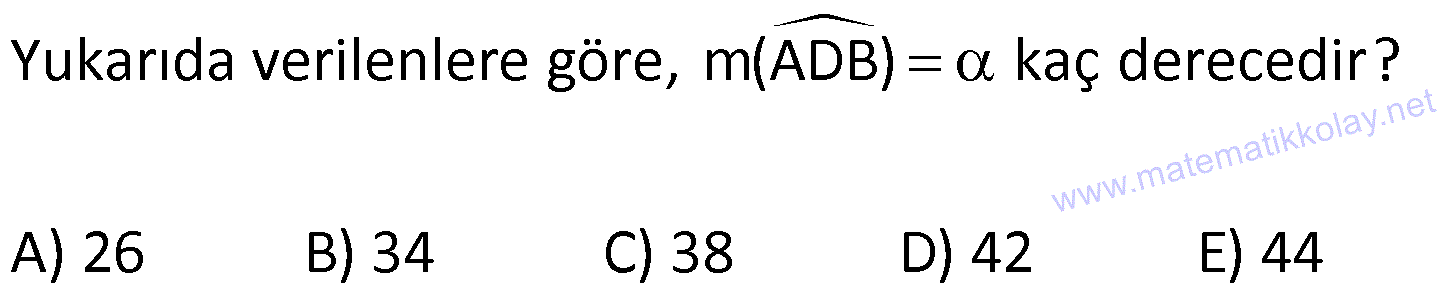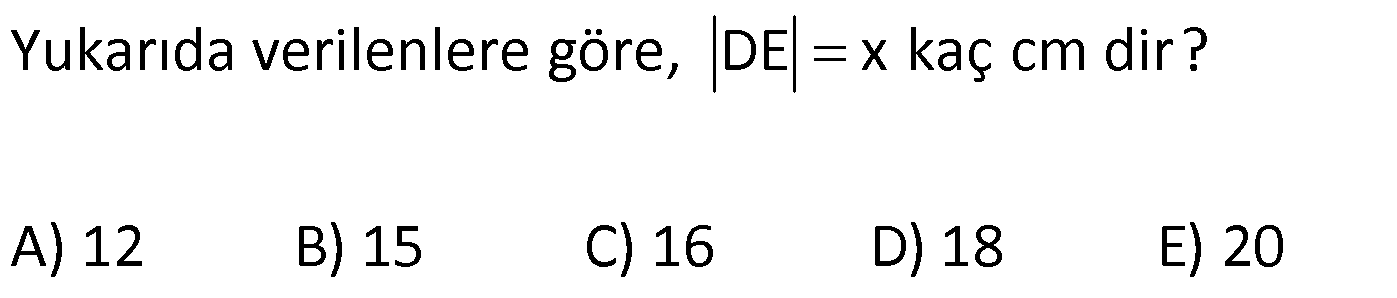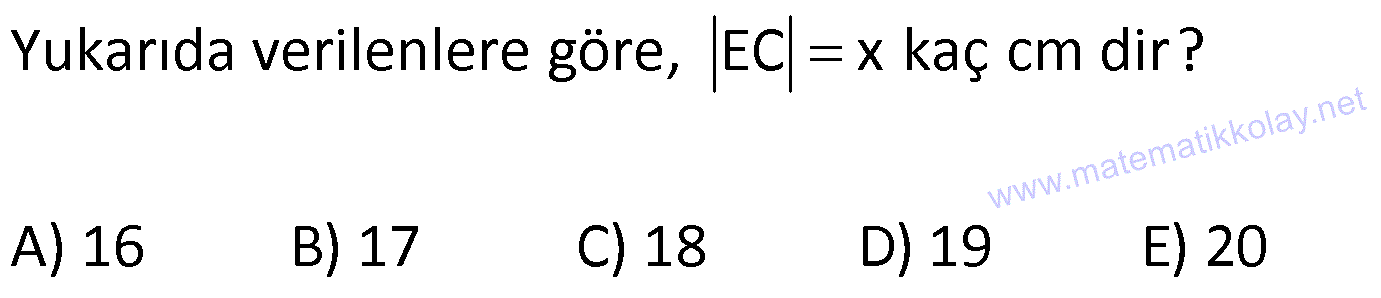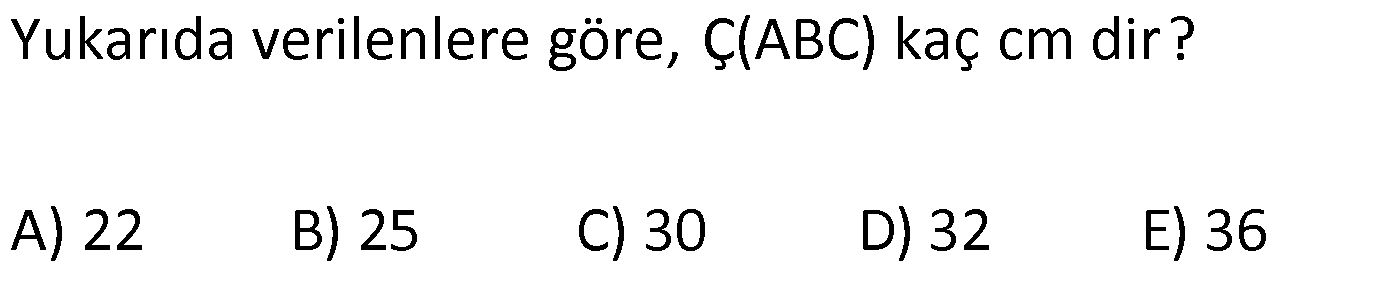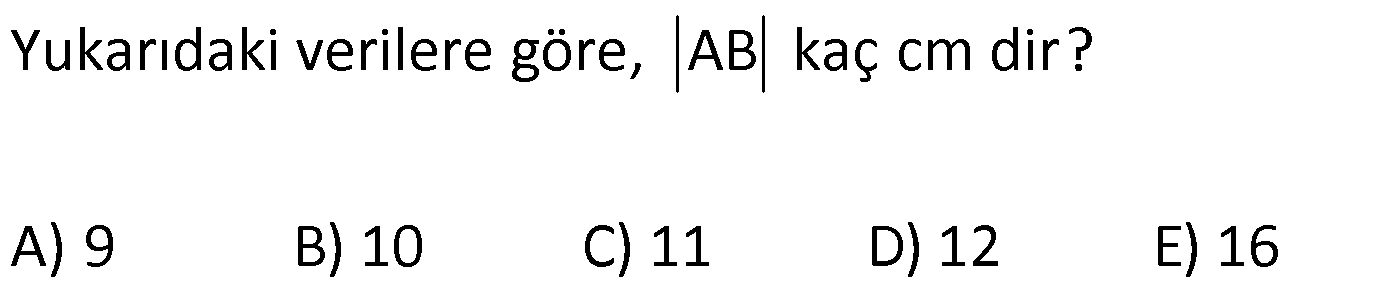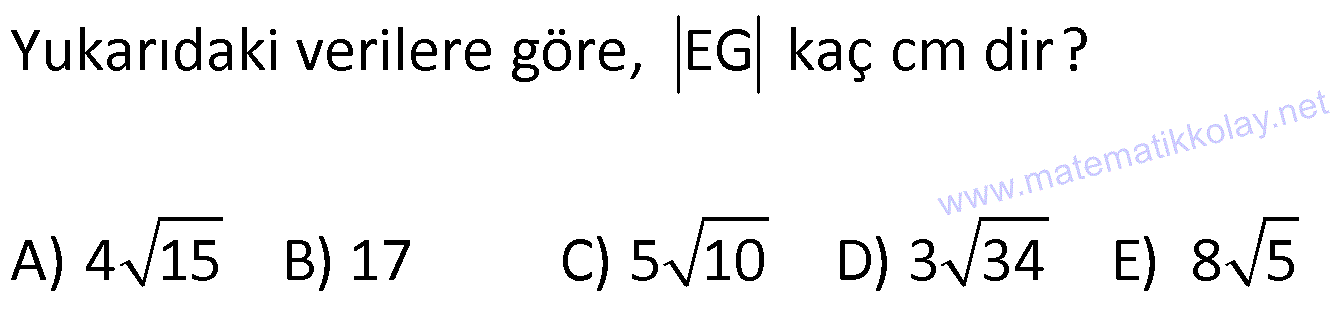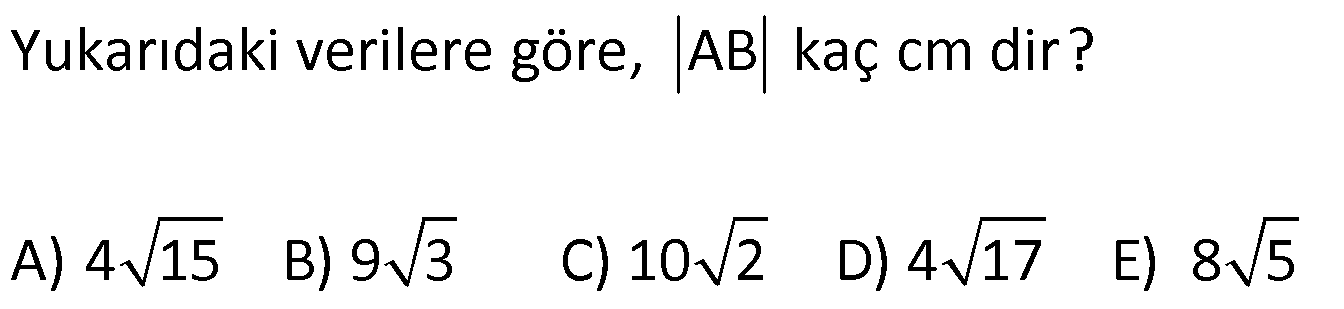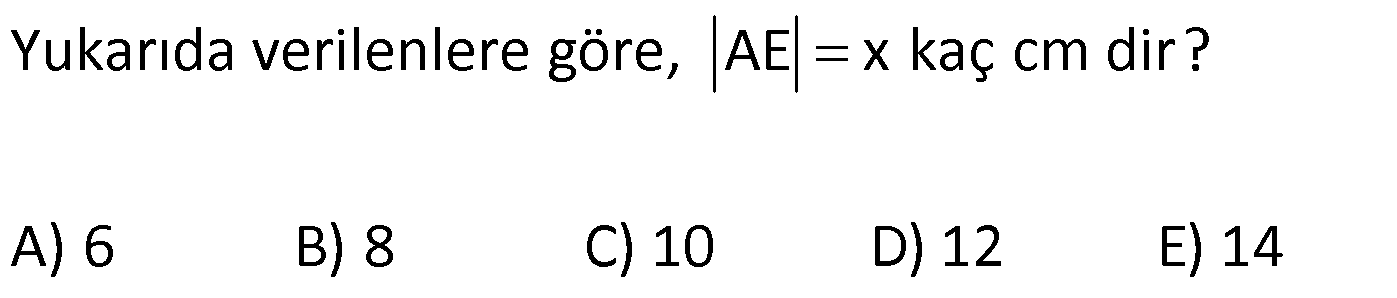Bu bölümde Deltoid ile ilgili 14 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
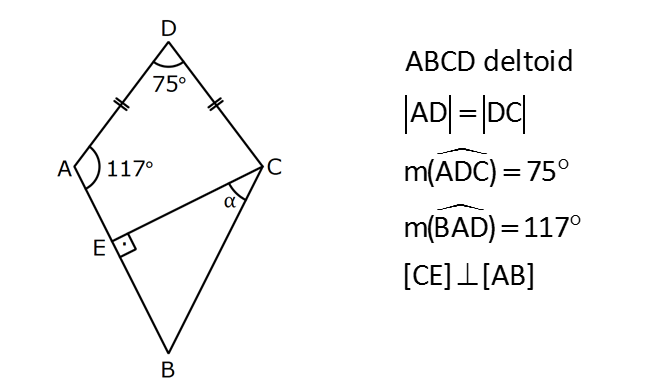
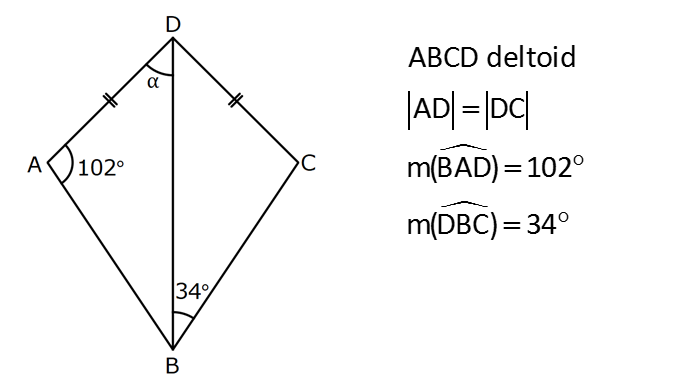
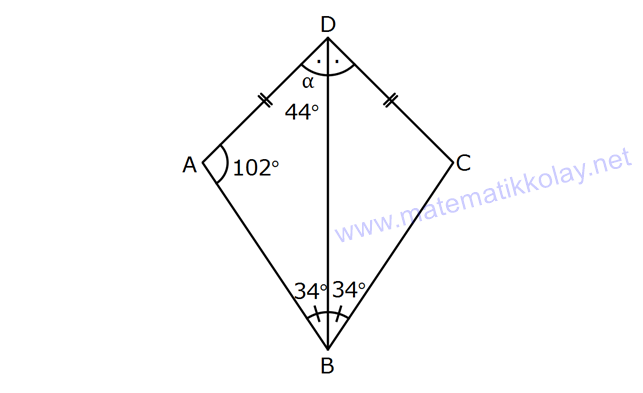
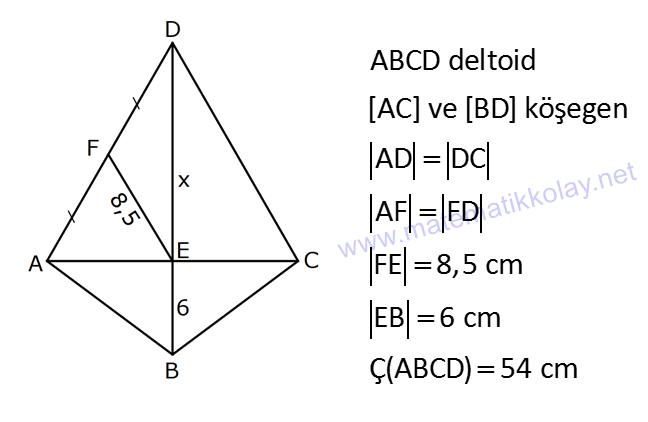
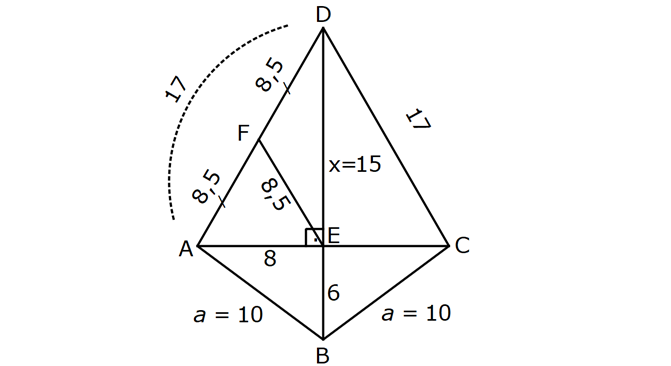
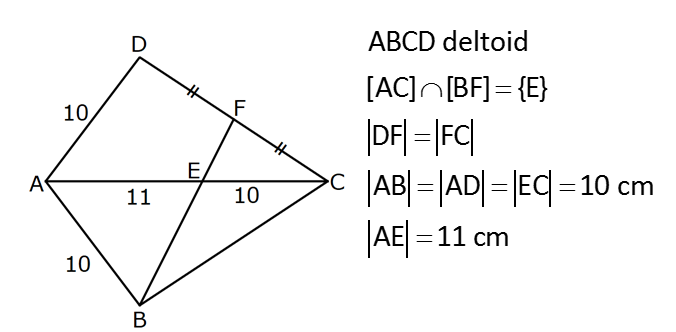
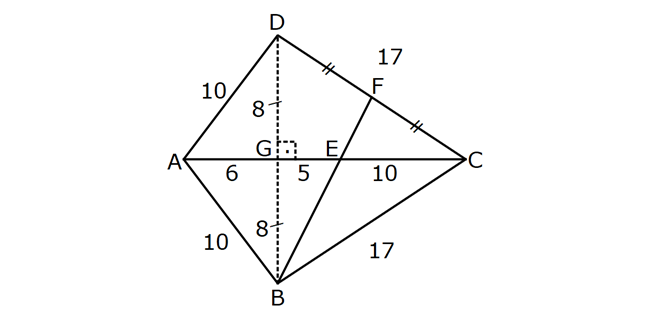
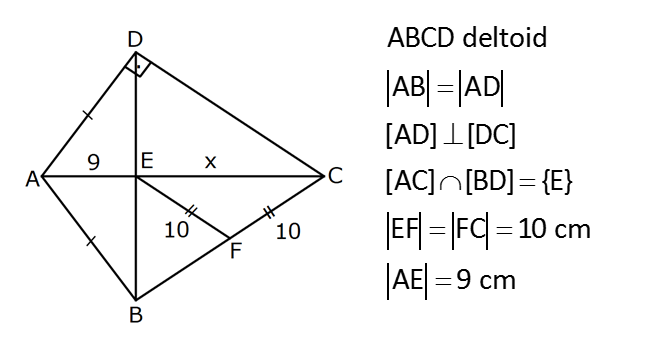
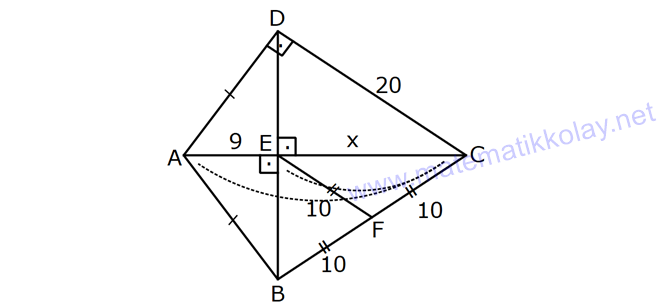
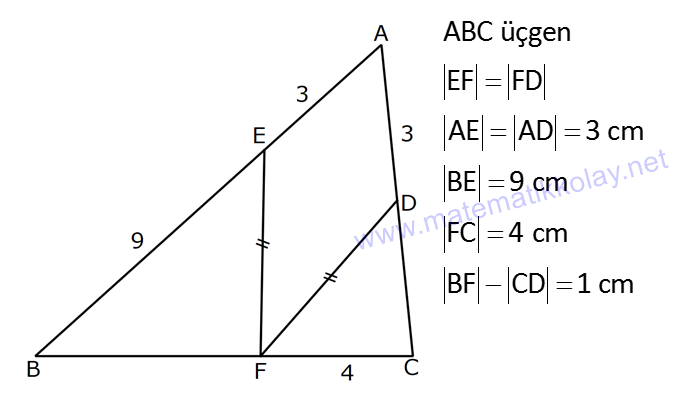
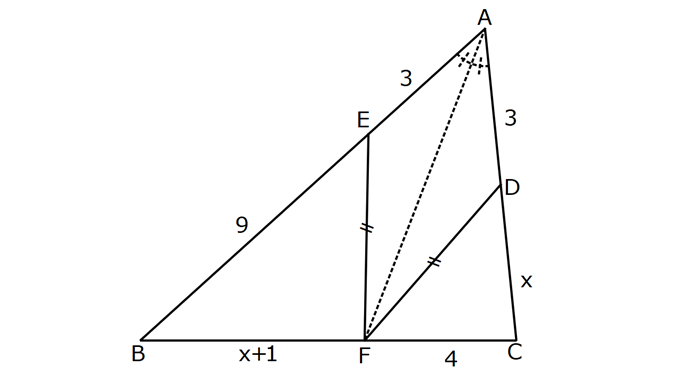
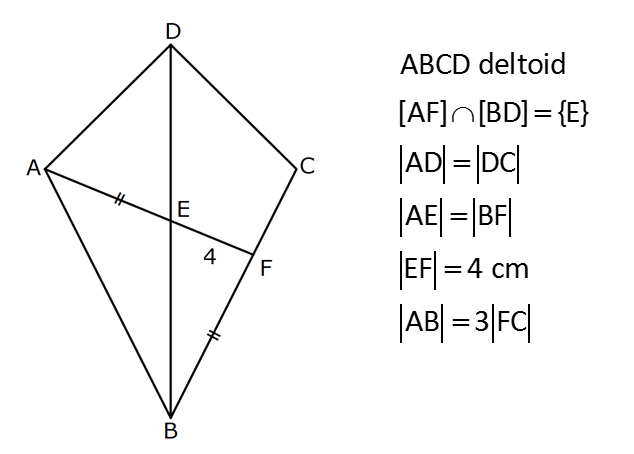
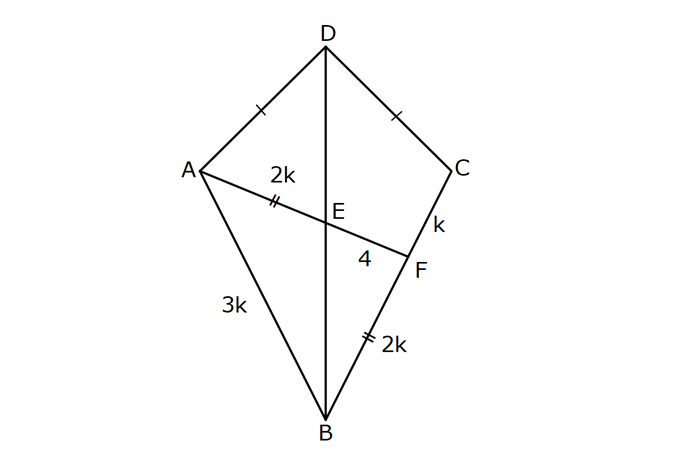
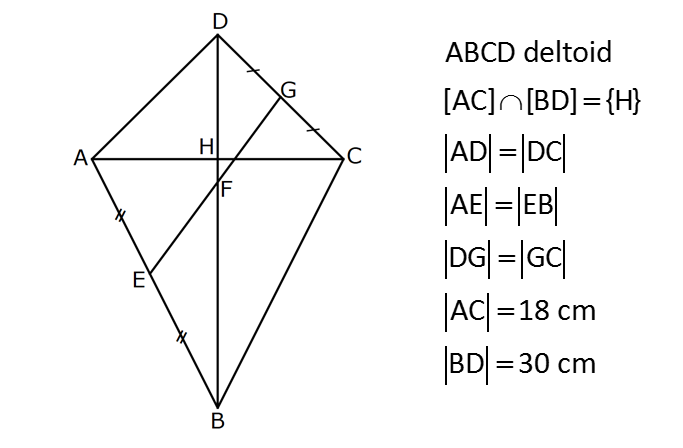
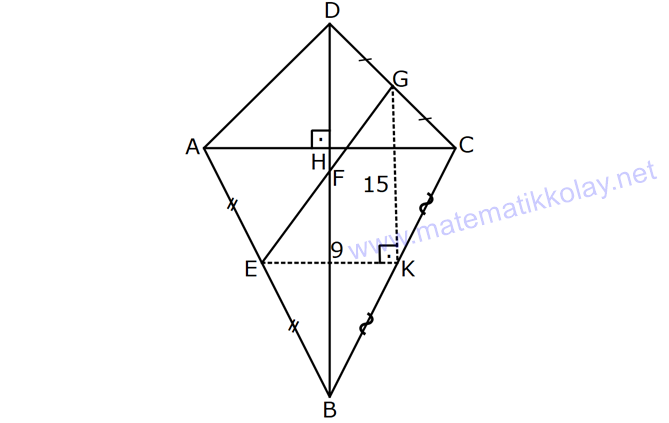
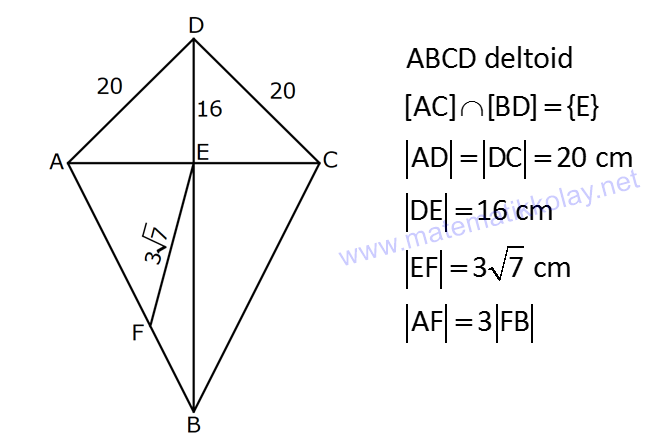
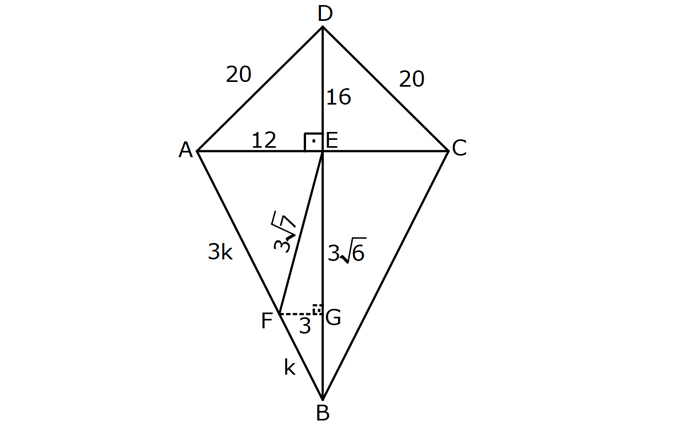
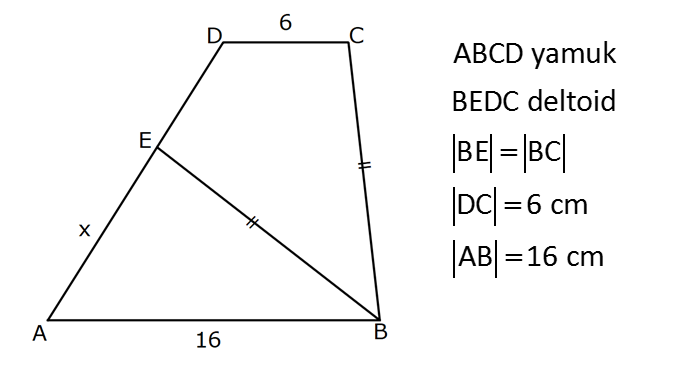
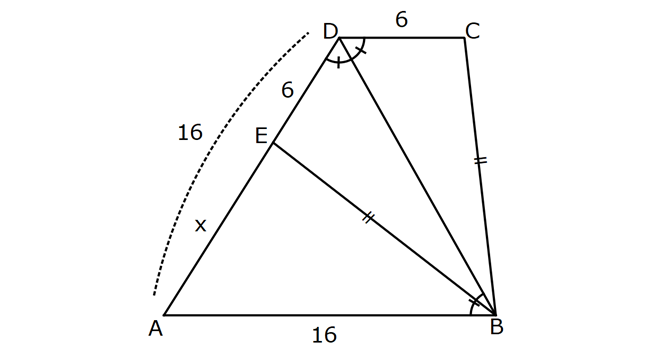
KAREDE AÇI UZUNLUK www.matematikkolay.net 1) ABCD deltoid AD DC m(ADC) 75 m(BAD) 117 [CE] [AB] Yukarıda verilenlere göre, m(BCE) kaç derecedir? A) 30 B) 32 C) 35 D) 39 E) 41 ÇÖZÜM: ABCD deltoid olduğundan dolayı m(BCD) 117 dir. Dörtgenlerin iç açıları toplamı 360 olduğundan m(B) 360 117 117 75 m(B) 360 309 51 dir. EBC dik üçgenine göre, 90 51 39 dir. Cevap : D Tabanları çakışık iki ikizkenar üçgenin birleşimi ile oluşan dörtgene denir. Tabanların birleştiği yerdeki açılar birbirine eşittir. (m(A) m(C) dir.) Not: deltoid 2) ABCD deltoid AD DC m(BAD) 102 m(DBC) 34 Yukarıda verilenlere göre, m(ADB) kaç derecedir? A) 26 B) 34 C) 38 D) 42 E) 44 ÇÖZÜM: Deltoid üzerinde ikizkenar üçgenlerin tepe açılarını birleştiren köşegen, açıortaydır. Aynı zamanda simetri eksenidir. Buna göre, m(ABD) 34 dir. ABD üçgeninin iç açıları toplamına göre, 102 3 Not: 4 180 136 180 44 dir. Cevap : E 3) www.matematikkolay.net ABCD deltoid [AC] ve [BD] köşegen AD DC AF FD FE 8,5 cm EB 6 cm Ç(ABCD) 54 cm Yukarıda verilenlere göre, DE x kaç cm dir ? A) 12 B) 15 C) 16 D) 18 E) 20 ÇÖZÜM: Deltoidin köşegenleri dik kesişir ve tepe açılarından gelen köşegen, diğer köşegeni iki eşit parçaya ayırır AE EC dir. . Buna göre, m(AED) 90 dir. Dik üçgende hipotenüsün kenarortayı muhteşe Not: m üçlüyü oluşturur. Buna göre, AF FE 8,5 cm dir. AD 17 cm olur. AB a olsun. Ç(ABCD) 54 cm ise, 17 17 a a 54 34 2a 54 2a 20 a 10 cm olur. O halde, ABE üçgeni bir 6 – 8 -10 üçgenidir. AE 8 cm olur. AED üçgeni d e bir 8 -15-17 üçgenidir. Bu sebeple x 15 cm olur. Cevap : B 4) ABCD deltoid [AC] [BF] {E} DF FC AB AD EC 10 cm AE 11 cm Yukarıda verilenlere göre, Ç(ABCD) kaç cm dir? A) 44 B) 46 C) 50 D) 53 E) 54 ÇÖZÜM: [BD] köşegenini çizelim. ABCD deltoid olduğundan dolayı [AC] köşegeni [BD] köşegenini iki eş parçaya ayırır. O halde, BDC üçgeninde iki kenarortay E noktasında kesişmiştir. E noktası ağırlık merkezidir, diyebiliriz. EC 10 cm ise, GE 5 cm dir. AG 11 5 6 cm kalır. AGD üçgeni bir 6 – 8 -10 üçgeni olduğu için GD 8 cm dir. DGC üçgeni de 8 -15-17 üçgeni olduğu için DC 17 cm dir. Buna göre, Ç(ABCD) 10 10 17 17 54 cm dir. Cevap : E 5) www.matematikkolay.net ABCD deltoid AB AD [AD] [DC] [AC] [BD] {E} EF FC 10 cm AE 9 cm Yukarıda verilenlere göre, EC x kaç cm dir ? A) 16 B) 17 C) 18 D) 19 E) 20 ÇÖZÜM: Deltoidin köşegenleri dik kesiştiği için E noktasında 90 lik açı oluşur. EF FC verildiği için BEC dik üçgeninde muhteşem üçlü oluşur. BC 10 10 20 cm olur. Deltoid olduğu için DC 20 cm dir. D noktasında 2 2 2 16.25 x 16 da 90 olduğu için öklit yapabiliriz. x(x 9) 20 x 9x 400 x 9x 400 0 (x 16)(x 25) 0 x 16 cm dir. Cevap : A 6) ABC üçgen EF FD AE AD 3 cm BE 9 cm FC 4 cm BF CD 1 cm Yukarıda verilenlere göre, Ç(ABC) kaç cm dir? A) 22 B) 25 C) 30 D) 32 E) 36 ÇÖZÜM: CD x cm olsun. BF x 1 cm olur. AEFD dörtgeni ise bir deltoittir. Çünkü iki ikizkenar üçgenin birleşimi ile oluşmuştur. Deltoidin tepe açılarını birleştiren köşegen açıortay – dır. Bu nedenle [AF] yi çizer 2 2 5.Eyl x 5 sek, açıortay olur. Açıortayın kuralını uygularsak 12 3 x olur. x 1 4 48 3x 3 x x 0 x 4x 45 0 (x 5)(x 9) x 5 cm dir. Ç(ABC) 9 3 3 5 4 6 30 cm dir. Cevap: C 7) www.matematikkolay.net ABCD deltoid [AF] [BD] {E} AD DC AE BF EF 4 cm AB 3 FC Yukarıdaki verilere göre, AB kaç cm dir? A) 9 B) 10 C) 11 D) 12 E) 16 ÇÖZÜM: 3k k AB 3 FC BF 3k k 2k olur. AE 2k olur. Deltoidin tepe açılarını birleştiren köşegen açıortay – dır. Bu nedenle [BE] bir açıortaydır. Açıortayın kuralını uygularsak 2 k 3 k 3 4 4k 12 k 3 cm dir. 2k AB 3k 9 cm buluruz. Cevap : A 8) ABCD deltoid [AC] [BD] {H} AD DC AE EB DG GC AC 18 cm BD 30 cm Yukarıdaki verilere göre, EG kaç cm dir? A) 4 15 B) 17 C) 5 10 D) 3 34 E) 8 5 ÇÖZÜM: K noktası [BC] nin orta noktası olsun. [EK], ABC üçgeninde orta taban olur. 18 EK 9 cm dir. 2 Ayrıca [GK], BCD üçgeninde orta taban olur. 30 GK 15 cm dir. 2 Orta tabanlar, kendi tabanlarına paralel oldukları 2 2 2 için K noktasında da dik açı oluşur. EKG dik üçgeninde pisagor yaparsak, EG 9 15 81 225 306 EG 306 9.34 3 34 cm dir. Cevap : E 9) www.matematikkolay.net ABCD deltoid [AC] [BD] {E} AD DC 20 cm DE 16 cm EF 3 7 cm AF 3 FB Yukarıdaki verilere göre, AB kaç cm dir? A) 4 15 B) 9 3 C) 10 2 D) 4 17 E) 8 5 ÇÖZÜM: 3a 4a 5a Deltoidin köşegenleri dik kesişeceği için E noktasında dik açı oluşur. AED üçgeni ise bir 12 -16 -20 üçgeni olduğundan AE 12 cm dir. [AE] ye paralel olarak [FG] yi çizelim. BFG üçgeni ile BAE üçgeni ar 2 2 2 2 2 2 2 2 asındaki benzerlikten k FG FG 3 cm dir. 4k 12 EFG üçgeninde pisagordan EG 3 3 7 EG 9 63 EG 54 EG 3 6 cm dir. 3 6 Yine benzerlikten, GB 6 cm dir. 3 EB 4 6 cm olur. AEB üçgeninde pisagordan AB 12 4 6 144 96 240 AB 240 16.15 4 15 cm dir. Cevap : A 10) ABCD yamuk BEDC deltoid BE BC DC 6 cm AB 16 cm Yukarıda verilenlere göre, AE x kaç cm dir ? A) 6 B) 8 C) 10 D) 12 E) 14 ÇÖZÜM: www.matematikkolay.net BEDC deltoid olduğundan dolayı [BD] açıortaydır. ABCD yamuk olduğundan dolayı, [DC] // [AB] dir. İç ters açılardan dolayı m(ABD) m(BDC) dir. Dolayısıyla ABD üçgeni ikizkenar üçgen olur. AD 16 cm dir. x 16 6 10 cm buluruz. Ce vap : C
