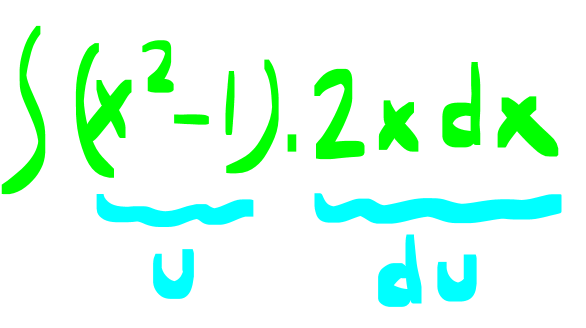Bu bölümde Belirsiz İntegralde Değişken Değiştirme Yöntemi ile ilgili 15 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
Çözüm için Tıklayınız.
2.SORU
| | | | | |
Çözüm için Tıklayınız.
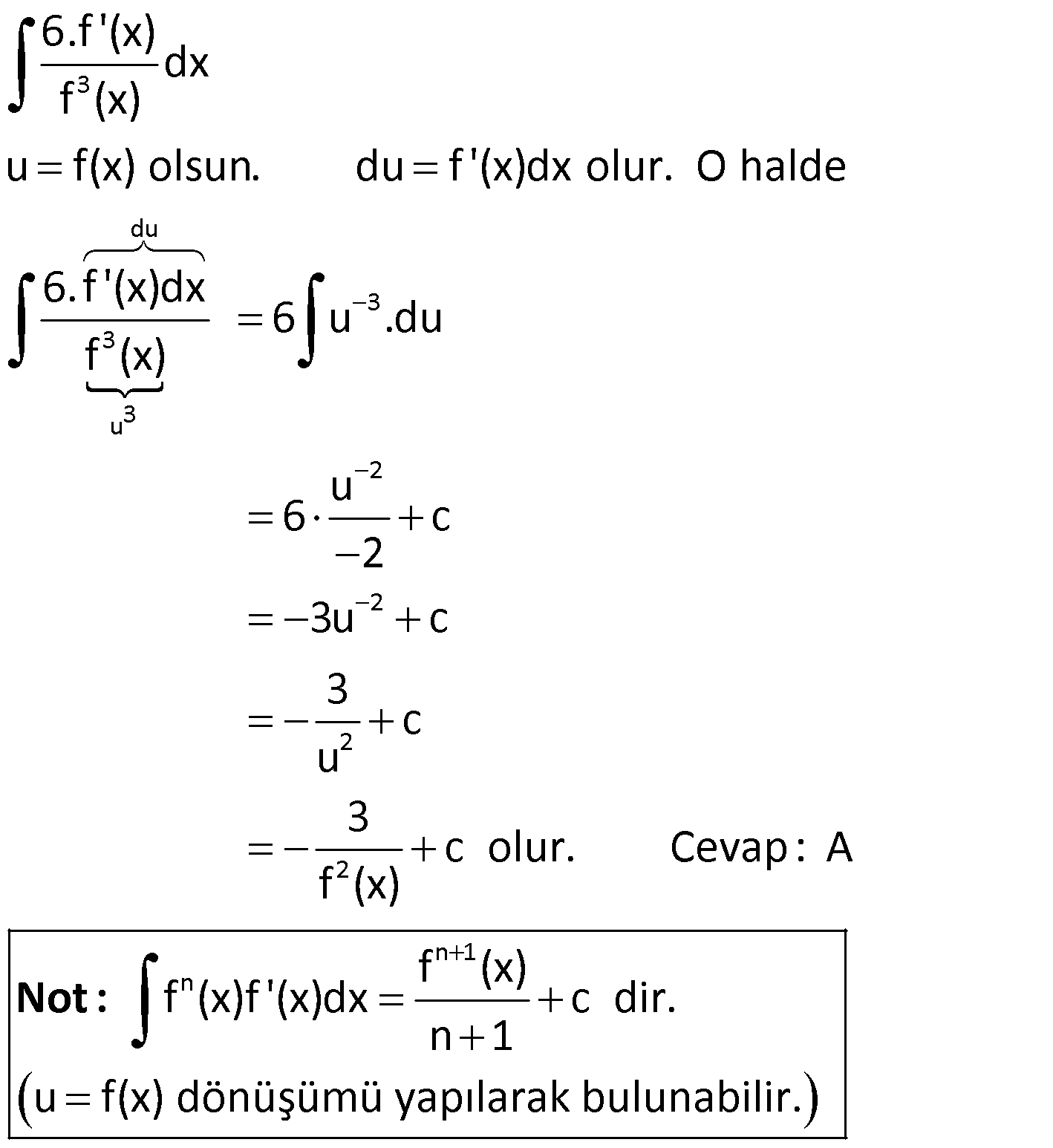
3.SORU
| | | | | |
Çözüm için Tıklayınız.
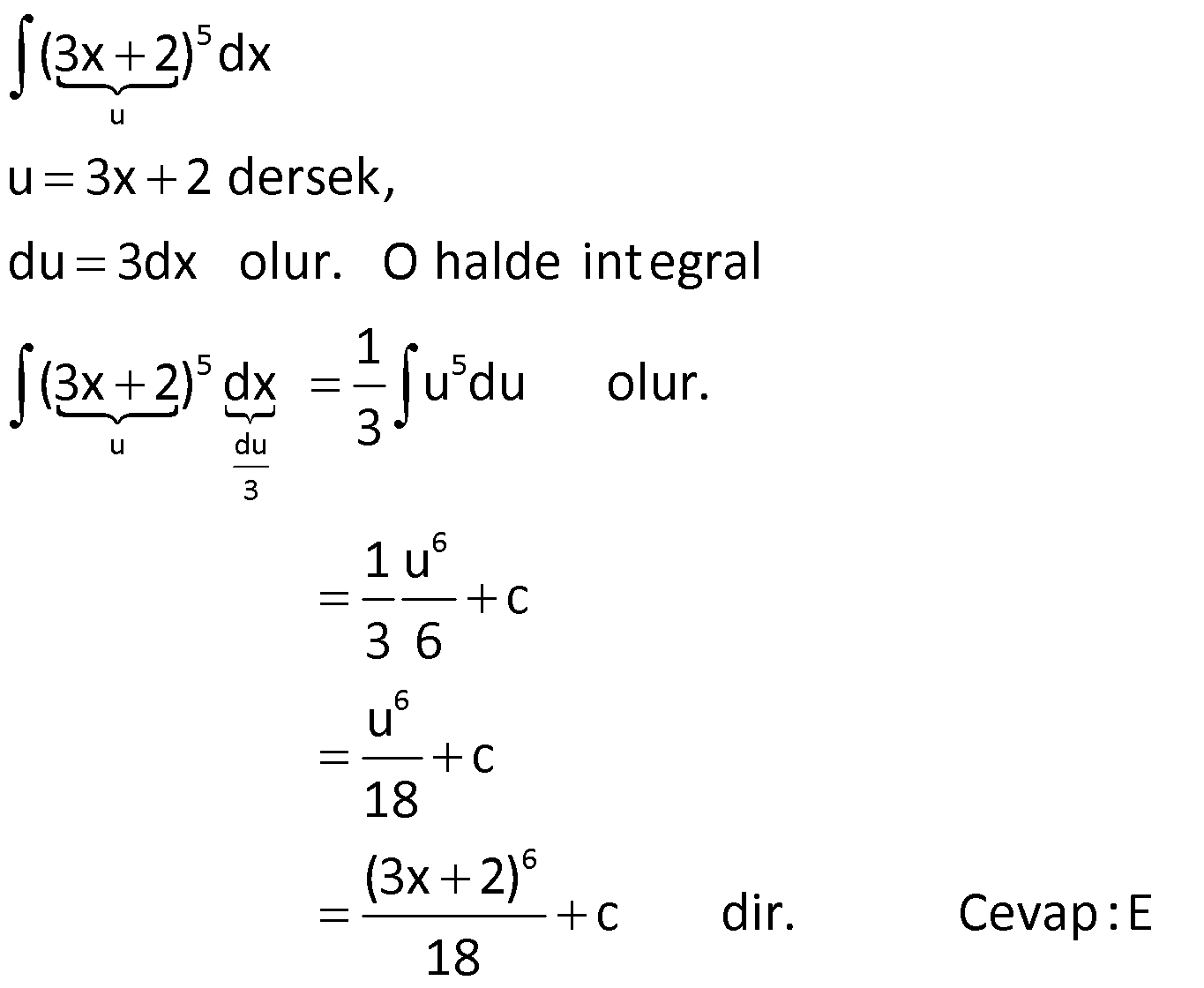
4.SORU
| | | | | |
Çözüm için Tıklayınız.
5.SORU
| | | | | |
Çözüm için Tıklayınız.
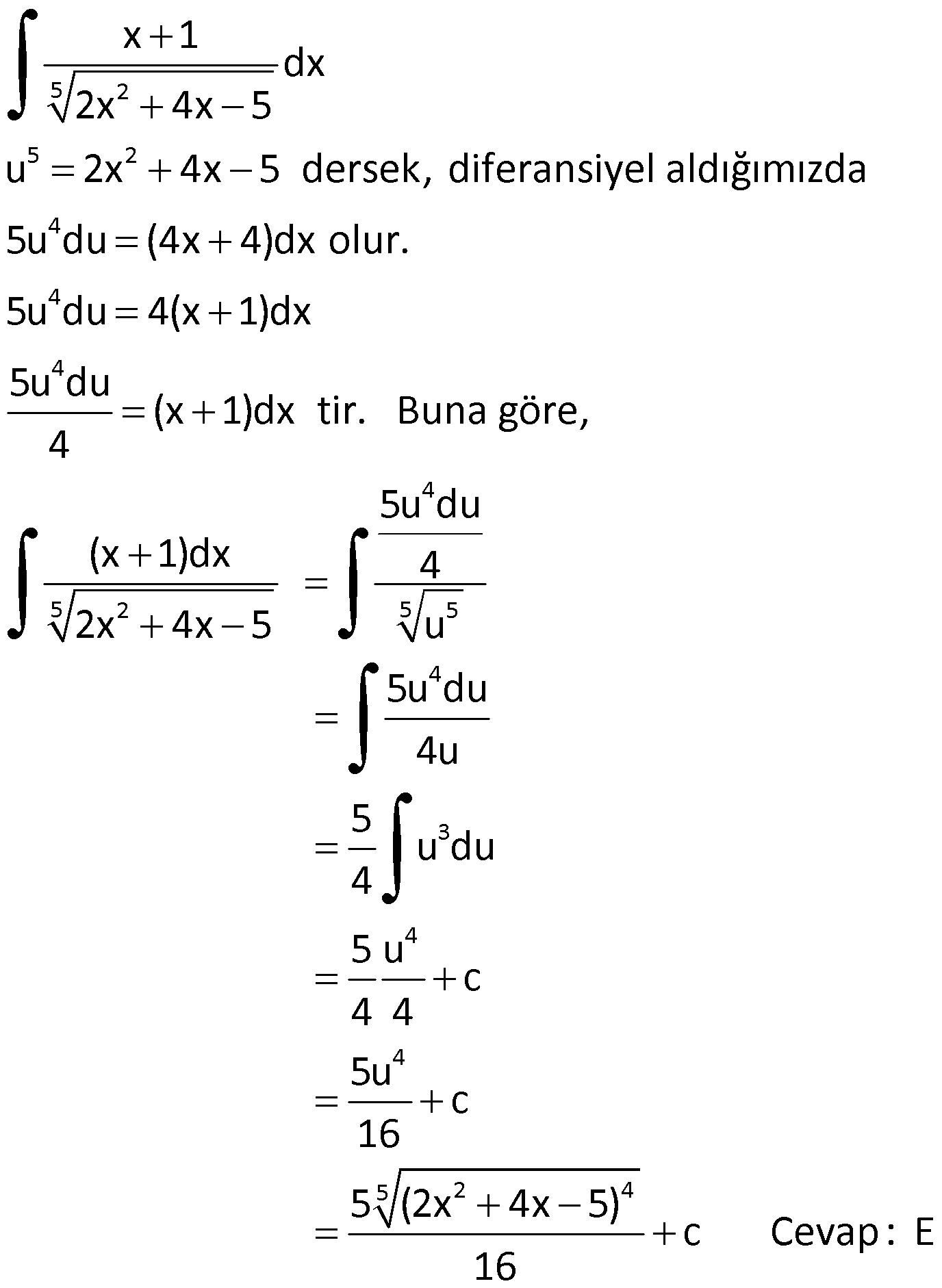
6.SORU
| | | | | |
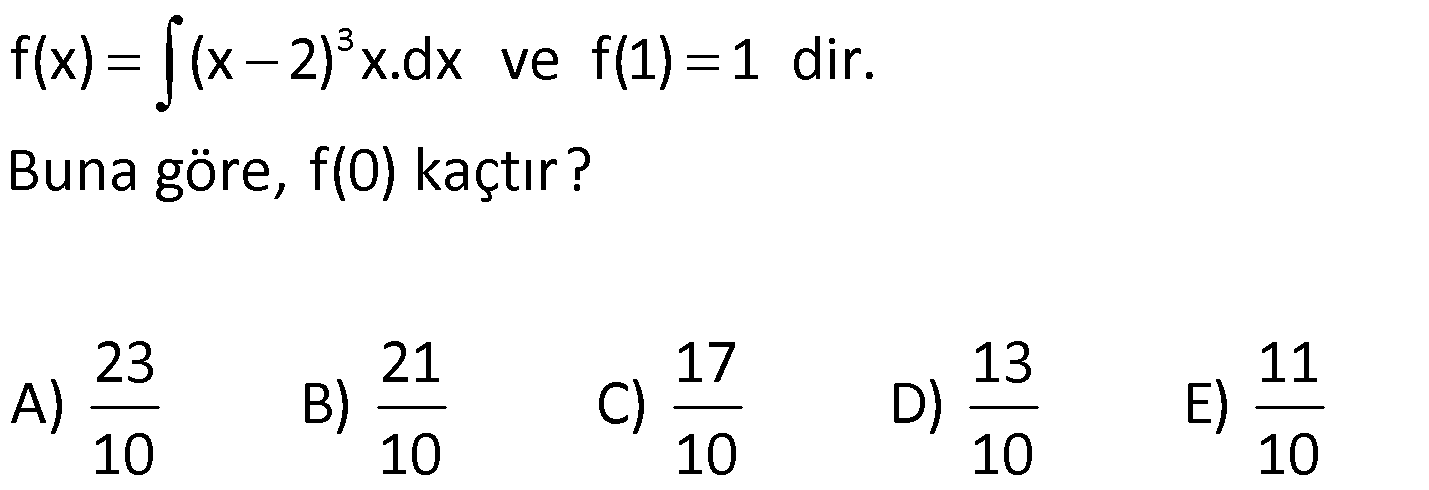
Çözüm için Tıklayınız.
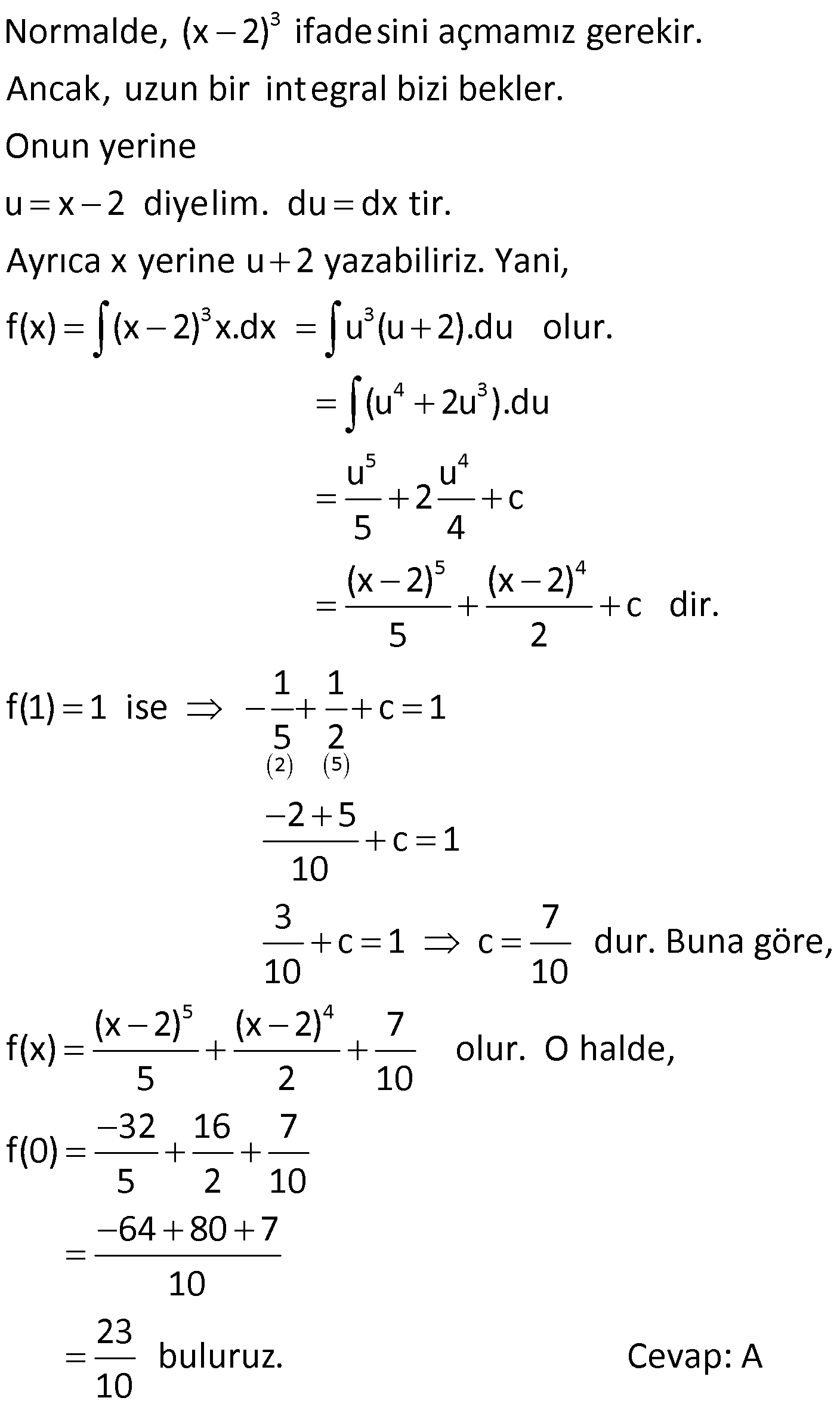
7.SORU
| | | | | |
Çözüm için Tıklayınız.
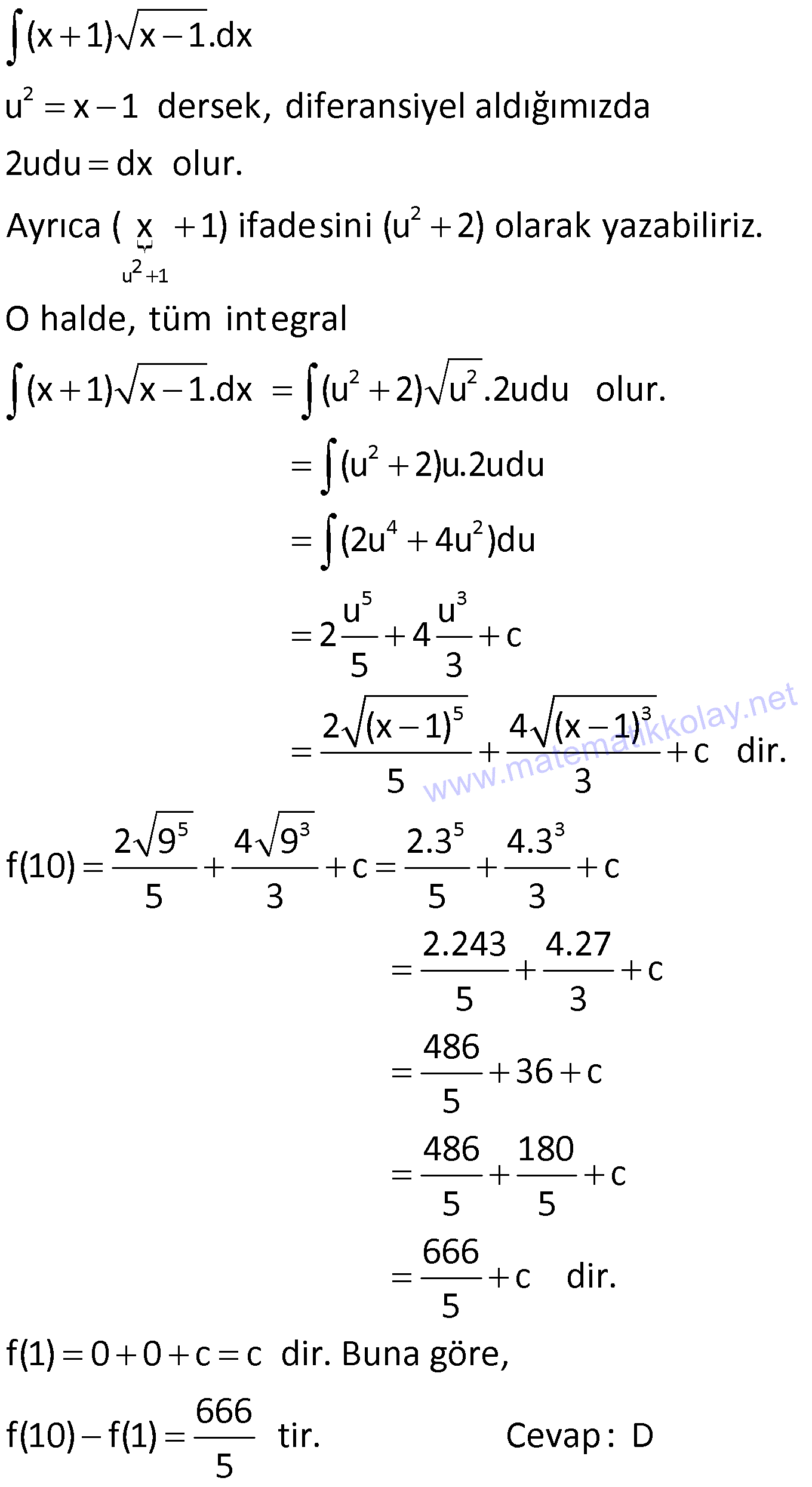
8.SORU
| | | | | |
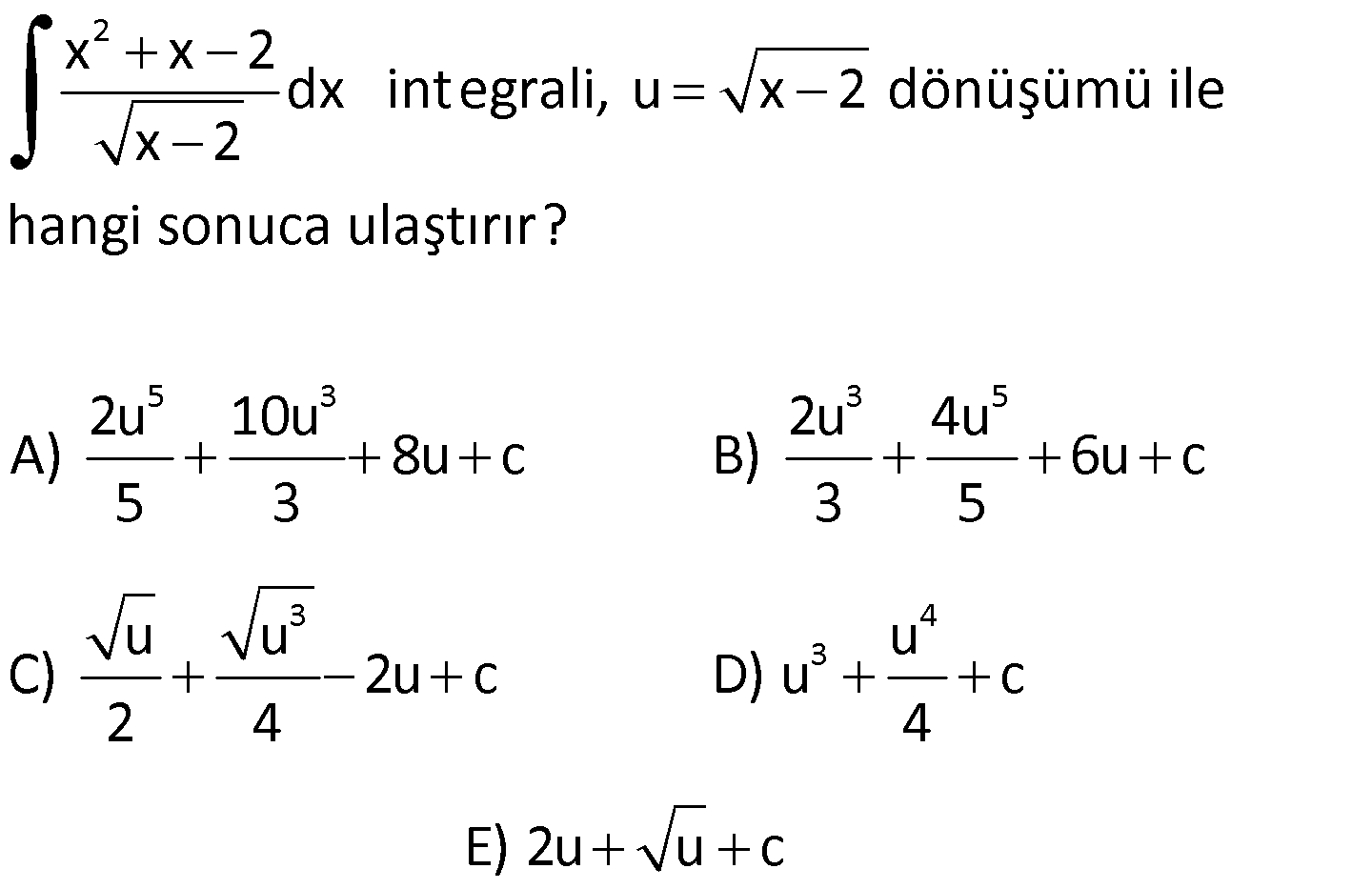
Çözüm için Tıklayınız.
9.SORU
| | | | | |
Çözüm için Tıklayınız.
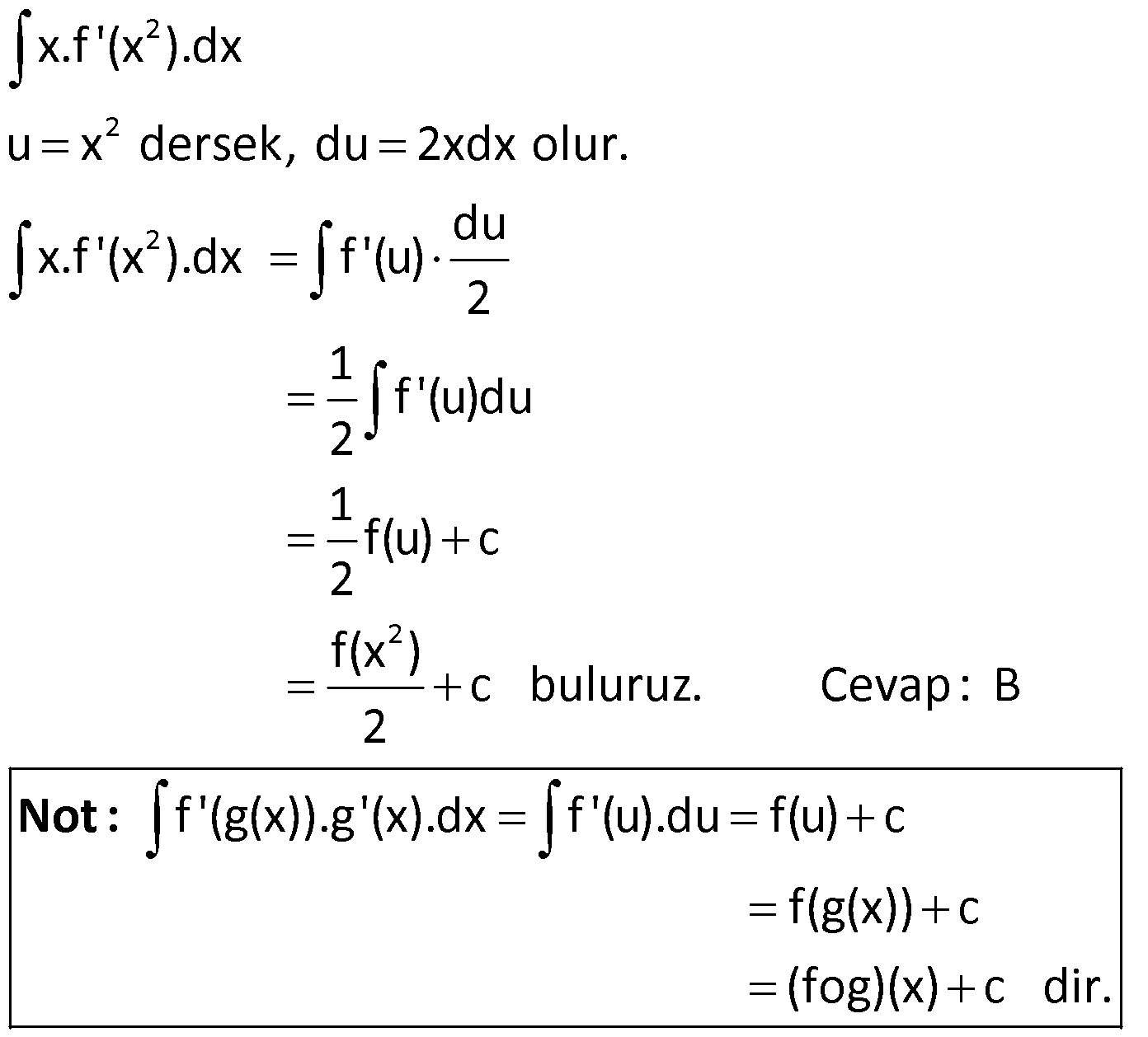
10.SORU
| | | | | |
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
DEĞİŞKEN DEĞİŞTİRME YÖNTEMİ www.matematikkolay.net 1) 5 3 4 6 5 6 4 5 4 4 4 5 4 (x 4) x dx integralinin sonucu aşağıdakilerden hangisidir? (x 4x)x x x (x 4) A) c B) c C) c 12 6 4 4 (x 4x) (x 4) D) c E) c 24 20 ÇÖZÜM: 5 3 4 u 5 5 4 4 Değişken değiştirme yöntemiyle, karışık olan ifadeleri daha basit hale getirebiliriz. (x 4) x dx u x 4 dersek, du d(x 4) 5x .dx tir. O halde, integralin içindeki x dx du yerine yazab 5 Not : 5 3 4 3 u du 5 4 4 5 4 iliriz. 1 (x 4) x dx u du olur. 5 1 u c 5 4 u c 20 (x 4) c dir. Cevap : E 20 2) 3 2 2 4 2 6.f'(x)dx integralinin sonucu aşağıdakilerden f (x) hangisidir? 3 24 A) c B) 12f (x) c C) c f (x) f (x) 12 1 D) c E ) c f(x) 4f (x) ÇÖZÜM: 3 du 3 3 3 u 2 2 2 8.f'(x) dx f (x) u f(x) olsun. du f'(x)dx olur. O halde 6.f'(x)dx 6 u .du f (x) u 6 c 2 3u c 3 c u 2 n 1 n 3 c olur. Cevap: A f (x) f (x) f (x)f'(x)dx c dir. n 1 u f(x) dönüşümü yapılarak bulunabilir. Not : 3) 5 6 6 6 6 6 (3x 2) dx integralinin sonucu aşağıdakilerden hangisidir? (3x 2) (3x 2) A) c B) c 6 2 C) 18(3x 2) c D) 6(3x 2) c (3x 2) E) c 18 ÇÖZÜM: 5 u 5 5 u du 3 6 6 6 (3x 2) dx u 3x 2 dersek, du 3dx olur. O halde integral 1 (3x 2) dx u du olur. 3 1 u c 3 6 u c 18 (3x 2) 18 c dir. Cevap :E www.matematikkolay.net 4) 2 3 3 3 2 3 3 3 3 3 3 3 3 2 2x x 4.dx integralinin sonucu aşağıdakilerden hangisidir? 2 (x 4) 9 (x 4) A) c B) c 3 4 4 (x 4) 3 (x 4) C) c D) c 9 2 2 (x 4) E) c 9 ÇÖZÜM: 2 n n n n 2 3 u 2 3 İntegralin içinde köklü ifade varsa, bu ifadeye kökten kurtulacak şekilde değişken vermek, kolaylık sağlayacaktır. Yani f(x) için f(x) u dersek, u u olarak çıkar. 2x x 4 .dx u x 4 ders Not : 2 2 3 2 2 2 ek, diferansiyel aldığımızda 2udu=3x dx olur. 2udu x dx tir. Buna göre, 3 2udu x 4.2x dx u .2 3 4 u.u.du 3 4 u .du 3 3 3 3 3 3 4 u c 3 3 4 x 4 c 9 4 (x 4) c dir. Cevap: C 9 5) 5 2 5 2 5 2 4 4 2 5 2 2 5 5 2 4 x 1 dx integralinin sonucu aşağıdakiler- 2x 4x 5 den hangisidir? 2x 4x 5 4 A) c B) c 4 5 (2x 4x 5) 5 (2x 4x 5) (2x 4x 5) C) c D) c 4 16 5 (2x 4x 5) E) c 16 ÇÖZÜM: 5 2 5 2 4 4 4 4 5 5 2 5 4 x 1 dx 2x 4x 5 u 2x 4x 5 dersek, diferansiyel aldığımızda 5u du (4x 4)dx olur. 5u du 4(x 1)dx 5u du (x 1)dx tir. Buna göre, 4 5u du (x 1)dx 4 2x 4x 5 u 5u du 4u 3 4 4 5 2 4 5 u du 4 5 u c 4 4 5u c 16 5 (2x 4x 5) c Cevap: E 16 6) 3 f(x) (x 2) x.dx ve f(1) 1 dir. Buna göre, f(0) kaçtır? 23 21 17 13 11 A) B) C) D) E) 10 10 10 10 10 ÇÖZÜM: www.matematikkolay.net 3 3 3 Normalde, (x 2) ifadesini açmamız gerekir. Ancak, uzun bir integral bizi bekler. Onun yerine u x 2 diyelim. du dx tir. Ayrıca x yerine u 2 yazabiliriz. Yani, f(x) (x 2) x.dx u (u 2).du olur. 4 3 5 4 5 4 2 5 (u 2u ).du u u 2 c 5 4 (x 2) (x 2) c dir. 5 2 1 1 f(1) 1 ise c 1 5 2 5 4 2 5 c 1 10 3 7 c 1 c dur. Buna göre, 10 10 (x 2) (x 2) 7 f(x) olur. O halde, 5 2 10 32 16 7 f(0) 5 2 10 64 80 7 10 23 buluruz. 10 Cevap: A 7) f(x) (x 1) x 1.dx olduğuna göre, f(10) f(1) kaçtır? 346 486 516 666 726 A) B) C) D) E) 5 5 5 5 5 ÇÖZÜM: 2 2 2 u 1 2 2 (x 1) x 1.dx u x 1 dersek, diferansiyel aldığımızda 2udu dx olur. Ayrıca ( x 1) ifadesini (u 2) olarak yazabiliriz. O halde, tüm integral (x 1) x 1.dx (u 2) u .2udu olur. 2 4 2 5 3 5 3 5 3 (u 2)u.2udu (2u 4u )du u u 2 4 c 5 3 2 (x 1) 4 (x 1) c dir. 5 3 2 9 4 9 2.3 f(10) c 5 3 5 3 4.3 c 5 3 2.243 4.27 c 5 3 486 36 c 5 486 180 c 5 5 666 c dir. 5 f(1) 0 0 c c dir. Buna göre, 666 f(10) f(1) tir. Cevap : D 5 8) 2 5 3 3 5 3 4 3 x x 2 dx integrali, u x 2 dönüşümü ile x 2 hangi sonuca ulaştırır? 2u 10u 2u 4u A) 8u c B) 6u c 5 3 3 5 u u u C) 2u c D) u c 2 4 4 E) 2u u c ÇÖZÜM: www.matematikkolay.net 2 2 2 2 4 2 2 2 4 2 2 u x 2 olacakmış. Kare alırsak u x 2 olur. Diferansiyel alırsak 2udu dx olur. x yi elde etmek için u x 2 eşitliğine bakalım. u 2 x kare alalım. u 4u 4 x olur. Buna göre, x x 2 u 4u 4 u 2 2 dx x 2 u 2 u 4 2 4 2 5 3 5 3 du u 5u 4 2 du 1 2 (u 5u 4)du u 5u 2 4u c 5 3 2u 10u 8u c dir. Cevap : 5 3 A 9) 2 2 2 2 2 x.f'(x ).dx integralinin sonucu aşağıdakilerden hangisidir? f(x ) A) 2f(x) c B) c 2 f (x) C) f (x) c D) c 2 E) 2f (x) c ÇÖZÜM: 2 2 2 2 x.f'(x ).dx u x dersek, du 2xdx olur. du x.f'(x ).dx f'(u) 2 1 f'(u)du 2 1 f(u) c 2 f(x ) c buluruz. Cevap : B 2 f'(g(x)).g'(x).dx f'(u).du f(u) c f(g(x)) c (fog)(x) c dir. Not : 10) f’ x dx integralinin sonucu aşağıdakilerden x hangisidir? f(x) A) f(x) c B) c 2 f x C) f x c D) c 2 E) 2f x c ÇÖZÜM: 2 f’ x dx x u x dersek, 2udu dx olur. Buna göre, f’ x f'(u) dx x u 2 u du 2 f'(u) du 2f(u) c 2f x c buluruz. Cevap: E
