11.SORU Çözüm için Tıklayınız.
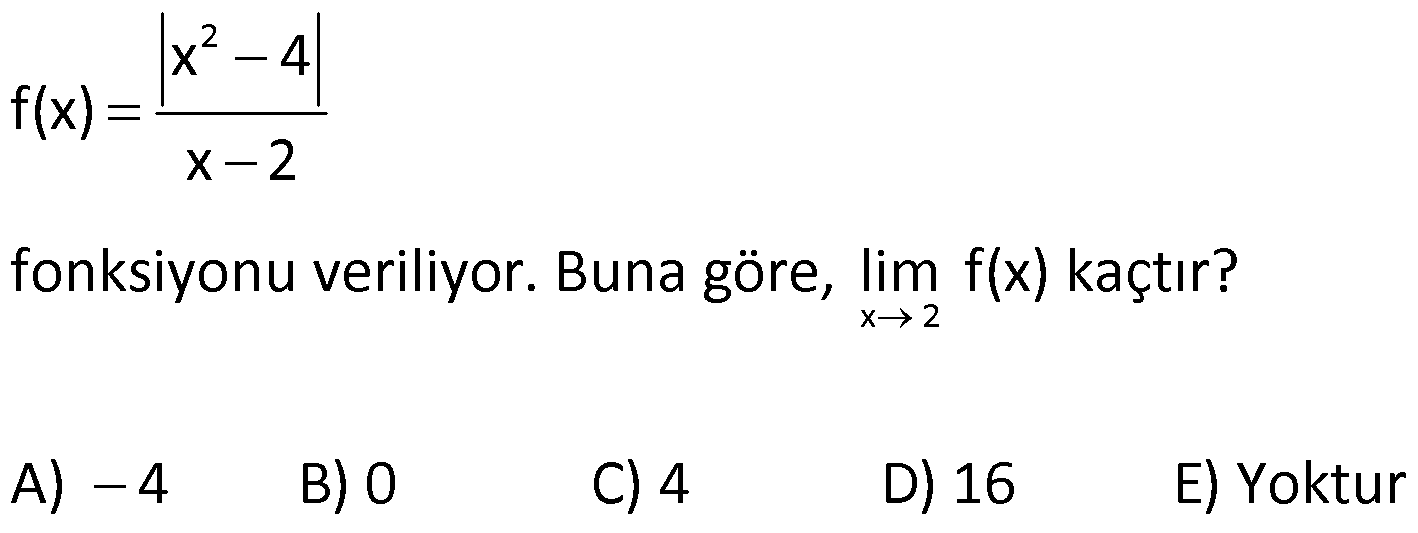
![]()
![]()
![]()
![]()
![]()

12.SORU Çözüm için Tıklayınız. 13.SORU Çözüm için Tıklayınız.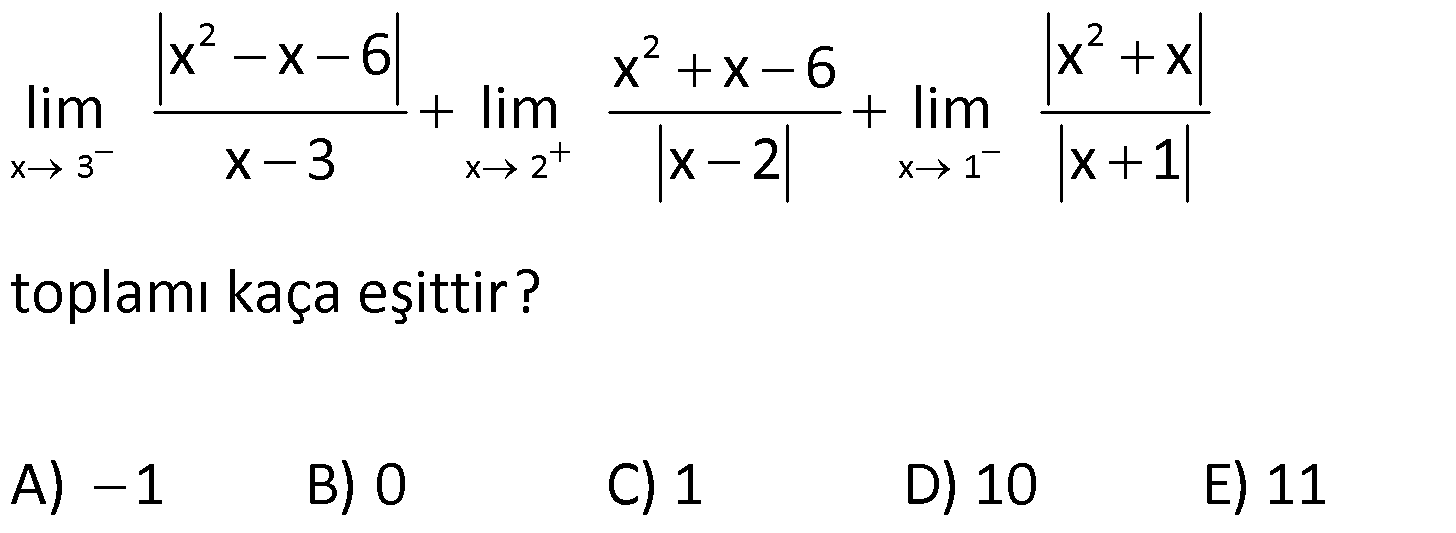
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
11) www.matematikkolay.net 2 x 2 x 4 f(x) x 2 fonksiyonu veriliyor. Buna göre, lim f(x) kaçtır? A) 4 B) 0 C) 4 D) 16 E) Yoktur Çözüm: Mutlak değerin içini 0 yapan nokta, kritik noktadır. Kritik noktalarda sağdan ve soldan limite bakmalıyız. Diğer noktalarda ise limit, fonksiyonun görüntüsüne eşittir. x 2 de ğeri, mutlak değer için k Not : içi negatif içi poz. ritik bir noktadır. Bu sebeple soldan ve sağdan limite bakmalıyız. x 2 x 2 (x 2) x 2 x 2 2 .(x 2) x 2 içi pozitif içi poz. 4 tür. x 2 x 2 (x 2) x 2 x 2 2 .(x 2) x 2 4 tür. Sağdan ve soldan limit farklı çıktığı için x 2 de limit yoktur. Cevap : E 12) 2 2 2 x 3 x 2 x 1 x x 6 x x x x 6 lim lim lim x 3 x 2 x 1 toplamı kaça eşittir? A) 1 B) 0 C) 1 D) 10 E) 11 Çözüm: 2 x 3 negatif pozitif x 3 x x 6 lim 3 değeri mutlak değerin içini x 3 0 yapıyor. Çarpanlarına ayırıp, işaret tespiti yapalım. x 3 x 2 (x 3) lim x 3 3 (x 2) x 3 2 2 x 2 pozitif 5 tir. x x 6 (x 3) (x 2) lim x 2 x 2 2 (x 1 değeri kritik nokta olmadığı için x 1 direkt x 1 yazarak lim it bulabiliriz) 5 tir. x x 1 1 2 lim 1 dir. x 1 1 1 2 Hepsini toplarsak, 5 5 1 1 buluruz. Cevap: C 13) x 2 x 0 x 2 lim 6x 12 yoktur. x lim 1 dir. x lim x x 4 0 dır. Yukarıdaki limit değerlerinden hangileri doğrudur? A) Yalnız I B) I ve II C) Yalnız III D) I ve III E) I. II. III. II ve III ÇÖZÜM: www.matematikkolay.net x 2 öncülü inceleyelim. lim 6x 12 x 2 değeri kritik noktadır. x 2 6x 12 12 12 0 a gidiyor. x 2 6x 12 12 12 0 a gidiyor. Bu sebeple limit vardır ve 0’a eşittir. I. öncül yanlış. öncülü incele I. II. x 0 negatif x yelim. lim 1 x x 0 değeri kritik noktadır. x x x 0 x x pozitif 1 e gidiyor. x x x 0 x x x 2 1 e gidiyor. Sağdan ve soldan limitler farklı olduğu için burada limit yoktur. II. öncül de yanlıştır. öncülü inceleyelim. lim x x 4 0 x 2 değeri mutlak değerin içini 0 yapıyor. Sağdan ve sold III. negatif x 2 x 2 x 2 x 2 x 2 2 x 2 an inceleyelim. lim x x 4 lim x ( (x 4)) lim x x 4 lim 2x 4 x 2 değeri mutlak değerin içini 0 yapıyor. Sağdan ve soldan inceleyelim. lim 2x 4 2x 4 0 dır. lim 2x 2 4 2x 4 0 dır. O halde, Iimit vardır ve 0 dır. III. öncül doğrudur. Cevap: C


6. Soru da limit 2 ve 3 ün limitleri yanlış yazılmış 2nin limiti yazılıp 3 ün limitine bakılmış . Aynı şekilde 3 ün limiti yazılıp 2 nin limitine bakılmış.
Çözümü inceledik ama hata göremedik. İki aşamalı olarak limite bakılıyor. f(2)=3 e gittiği için (fof)(2) bileşke fonksiyonu f(3) e dönüşüyor.