Çarpanlara Ayırma (Latex Formatı)

Çarpanlara Ayırma konusu ile ilgili 2 Test bulunmakta olup; 1.’sine ait 20 adet soru ve çözümü bu sayfada yer almaktadır. Sorularınızı çözdükten sonra “Doğru Cevap” seçeneğine tıklayarak doğru şıkkı görebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…


SORULAR

SORU 1


\displaystyle {{(x-y)}^{2}}+3(y-x)
ifadesinin çarpanlarından biri aşağıdakilerden hangisidir?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }-x+y+2\text{ }} & {B)\text{ }x-y-3} & {C)\text{ }-x+y} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }x-y+3} & {E)\text{ }x-y} \end{array}\end{array}

Doğru Cevap Çözüm için Tıklayınız

SORU 2

\displaystyle {{a}^{6}}-{{a}^{4}}+{{a}^{2}}-1

ifadesinin çarpanlarından biri aşağıdakilerden hangisidir?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }{{a}^{3}}+1\text{ }} & {B)\text{ }{{a}^{4}}+a} & {C)\text{ }{{a}^{4}}+1} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }{{a}^{4}}-1} & {E)\text{ }{{a}^{2}}+1} \end{array}\end{array}

Doğru Cevap Çözüm için Tıklayınız

SORU 3

\displaystyle \begin{array}{l}\text{ }a-b=5\\\text{ }x-y=3\text{ }\end{array}
olduğuna göre, \displaystyle ax+by-ay-bx işleminin sonucu kaçtır?

A) 15    B) 25    C) 27    D) 45     E) 60

Doğru Cevap Çözüm için Tıklayınız

SORU 4

\displaystyle \begin{array}{l}\text{ }{{x}^{2}}+xy=20\\\text{ }{{y}^{2}}+xy=5\end{array}

olduğuna göre, \displaystyle x-y nin pozitif değeri kaçtır?

A) 1    B) 2     C) 3     D) 4      E) 5

Doğru Cevap Çözüm için Tıklayınız

SORU 5

\displaystyle \text{ }x-y=3\text{ ve }{{\text{x}}^{2}}+{{\text{y}}^{2}}=29

olduğuna göre, \displaystyle x+y nin pozitif değeri kaçtır?

A) 3    B) 4     C) 5     D) 6     E) 7

Doğru Cevap Çözüm için Tıklayınız

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

SORU 6

\displaystyle a-\frac{3}{a}=5

olduğuna göre, a+\frac{3}{a} nın pozitif değeri kaçtır?

A) 19     B) 21     C) 31    D) 33      E) 37

Doğru Cevap Çözüm için Tıklayınız

SORU 7

\displaystyle 4{{x}^{2}}-7x-4=0

olduğuna göre, x^2+\frac{1}{x^2} toplamının değeri kaçtır?

\displaystyle \begin{array}{*{20}{l}} {A)\text{ }\frac{{49}}{{16}}\text{ }} & {B)\text{ }\frac{{81}}{{16}}} & {C)\text{ }\frac{{81}}{{49}}} & {D)\text{ }\frac{{91}}{{49}}\text{ }} & {E)\text{ }\frac{{81}}{{25}}} \end{array}

Doğru Cevap Çözüm için Tıklayınız

SORU 8

\displaystyle \text{ }{{a}^{2}}+{{b}^{2}}+{{c}^{2}}=11
\displaystyle \text{ }ab+ac+bc=7

olduğuna göre, \displaystyle a+b+c nin pozitif değeri kaçtır?

\displaystyle \begin{array}{*{20}{l}} {A)\text{ }5\text{ }} & {B)\text{ }6} & {C)\text{ }7} & {D)\text{ }8} & {E)\text{ }10} \end{array}

Doğru Cevap Çözüm için Tıklayınız

SORU 9

\displaystyle \text{ }{{\text{x}}^{2}}-9{{y}^{2}}=48
\displaystyle \text{ }x+3y=12

olduğuna göre, y kaçtır?

\displaystyle \begin{array}{*{20}{l}} {A)\text{ }\frac{1}{3}\text{ }} & {B)\text{ }2} & {C)\text{ }\frac{4}{3}} & {D)\text{ }2} & {E)\text{ }\frac{5}{2}} \end{array}

Doğru Cevap Çözüm için Tıklayınız

SORU 10

\displaystyle \text{ }x-y=24\text{ }ve
\displaystyle \text{ }\sqrt{x}-\sqrt{y}=4

olduğuna göre, x + y kaçtır?

A) 22     B) 26      C) 28      D) 32      E) 35

Doğru Cevap Çözüm için Tıklayınız

SORU 11

\displaystyle \sqrt{{98.102+4}}

işleminin sonucu kaçtır?

A) 94      B) 96     C) 98     D) 100      E) 102

Doğru Cevap Çözüm için Tıklayınız

SORU 12

\displaystyle \text{ a}-b=b-c=8
olduğuna göre,  \displaystyle {{\text{a}}^{2}}+{{c}^{2}}-2{{b}^{2}} ifadesinin değeri kaçtır?

A) 64     B) 72    C) 96     D) 108     E) 128

 

Doğru Cevap Çözüm için Tıklayınız

SORU 13

\displaystyle \text{ }x=\sqrt[3]{6}-1
olduğuna göre, \displaystyle {{\text{x}}^{3}}+3{{x}^{2}}+3x-3 ifadesinin değeri kaçtır?

A) 1    B) 2      C) 3      D) 4      E) 5

Doğru Cevap Çözüm için Tıklayınız

SORU 14

\displaystyle \text{ }{{x}^{3}}-3{{x}^{2}}y=75
\displaystyle \text{ }{{\text{y}}^{3}}-3x{{y}^{2}}=11

olduğuna göre, \displaystyle x-y ifadesinin değeri kaçtır?

A) 1     B) 2     C) 3      D) 4       E) 5

Doğru Cevap Çözüm için Tıklayınız

SORU 15

\displaystyle \text{ }a+b=4
\displaystyle \text{ }{{a}^{2}}+{{b}^{2}}=8

olduğuna göre, a³ + b³ ifadesinin değeri kaçtır?

A) 11    B) 12    C) 13    D) 14     E) 16

Doğru Cevap Çözüm için Tıklayınız

SORU 16

\displaystyle \text{ x}-\frac{3}{x}=2

olduğuna göre, x^3-\frac{27}{x^3} kaçtır?

A) 26     B) 30    C) 34     D) 38    E) 40

Doğru Cevap Çözüm için Tıklayınız

SORU 17

\displaystyle \text{ }{{4}^{x}}-{{2}^{{x+1}}}-15

ifadesinin çarpanlarından biri aşağıdakilerden hangisidir?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }{{2}^{x}}+3\text{ }} & {B)\text{ }{{2}^{x}}-4\text{ }} & {C)\text{ }{{2}^{x}}+6\text{ }} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }{{2}^{x}}-1\text{ }} & {E)\text{ }{{2}^{x}}+1\text{ }} \end{array}\end{array}

Doğru Cevap Çözüm için Tıklayınız

SORU 18

\displaystyle \text{ }A={{x}^{2}}-6x+15

ifadesinin en küçük değeri kaçtır?

A) 2    B) 6     C) 12       D) 15       E) 18

Doğru Cevap Çözüm için Tıklayınız

SORU 19

\displaystyle \text{ }{{x}^{2}}+4{{y}^{2}}-8x+12y+25=0

olduğuna göre, x.y çarpımı kaçtır?

A) 16    B) 12     C) 6     D) 4      E) 18

Doğru Cevap Çözüm için Tıklayınız

SORU 20

\displaystyle \text{ }\frac{{{{a}^{2}}b+a{{b}^{2}}-ab}}{{{{a}^{2}}+ab-a}}

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }a-b\text{ }} & {B)\text{ }b\text{ }} & {C)\text{ }a\text{ }} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }b-a\text{ }} & {E)\text{ }a+b\text{ }} \end{array}\end{array}

Doğru Cevap Çözüm için Tıklayınız
Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

SORU ÇÖZÜMLERİ

ÇÖZÜM 20

Ortak paranteze alarak çözüme başlayalım.

\displaystyle \frac{{{{a}^{2}}b+a{{b}^{2}}-ab}}{{{{a}^{2}}+ab-a}}=\frac{{ab(a+b-1)}}{{a(a+b-1)}}=b\text{ buluruz}\text{.}

Doğru Cevap : B şıkkı

Soruyu Gör
Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

ÇÖZÜM 19

\displaystyle {{x}^{2}}+4{{y}^{2}}-8x+12y+25=0 eşitliğinde iki tane
tam kare ifade bulmaya çalışalım.

\displaystyle {{x}^{2}}+4{{y}^{2}}-8x+12y+\underbrace{{25}}_{{9+16}}=0
\displaystyle {{x}^{2}}+4{{y}^{2}}-8x+12y+9+16=0
\displaystyle \underbrace{{{{x}^{2}}-8x+16}}_{{}}+\underbrace{{4{{y}^{2}}+12y+9}}_{{}}=0
\displaystyle \underbrace{{{{{(x-4)}}^{2}}}}_{0}+\underbrace{{{{{(2y+3)}}^{2}}}}_{0}=0
\displaystyle x-4=0\text{ }\Rightarrow \text{ }x=4
\displaystyle 2y+3=0\text{ }\Rightarrow \text{ }y=-\frac{3}{2}

Buna gore;\displaystyle x.y=4\cdot \left( {-\frac{3}{2}} \right)=-6 buluruz.

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 18

\displaystyle A={{x}^{2}}-6x+15 ifadesinin içindeki tam kare ifadeyi bulalım.

\displaystyle {{x}^{2}}-6x+15=\underbrace{{{{x}^{2}}-6x+9}}_{{Tam\text{ }kare}}+6
\displaystyle =\underbrace{{{{{(x-3)}}^{2}}}}_{{en\text{ }az\text{ }0}}+6

En küçük 6 olabilir.

Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 17

\displaystyle {{4}^{x}}-{{2}^{{x+1}}}-15 ifadesini daha rahat çarpanlarına
ayırabilmek için, \displaystyle a={{2}^{x}} diyerek değişken değiştirelim. Buna göre;
\displaystyle {{4}^{x}}-{{2}^{{x+1}}}-15={{\left( {{{2}^{x}}} \right)}^{2}}-{{2.2}^{x}}-15
\displaystyle \begin{array}{l}={{a}^{2}}-2a-15\\\text{ }a\text{ }-5\\\text{ }a\text{ }3\end{array}
\displaystyle =(a-5)(a+3)\text{ }(a={{2}^{x}})
\displaystyle =({{2}^{x}}-5)({{2}^{x}}+3)\text{ buluruz}\text{.}

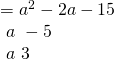
\displaystyle {{2}^{x}}+3 çarpanı A şıkkında vardır.

Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 16

\displaystyle {{x}^{3}}-\frac{{27}}{{{{x}^{3}}}}

ifadesinı iki küp farkından yararlanarak bulalım. Buna göre;

\displaystyle {{x}^{3}}-\frac{{27}}{{{{x}^{3}}}}={{\left( {x-\frac{3}{x}} \right)}^{3}}+3x\frac{3}{x}\left( {x-\frac{3}{x}} \right)
\displaystyle \text{ }={{\left( {x-\frac{3}{x}} \right)}^{3}}+9\left( {x-\frac{3}{x}} \right)
\displaystyle \text{ }={{\left( 2 \right)}^{3}}+9\left( 2 \right)
\displaystyle \text{ }=8+18
\displaystyle \text{ }=26\text{ }buluruz.

Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 15

İki küp toplamı;

\displaystyle {{a}^{3}}+{{b}^{3}}=(a+b)\cdot ({{a}^{2}}-ab+{{b}^{2}})\text{ }dir.
\displaystyle {{a}^{3}}+{{b}^{3}}=(a+b)\cdot ({{a}^{2}}-\underbrace{{ab}}_{{Bilmiyoruz}}+{{b}^{2}})

Bu eşitlikte ab çarpımını bilmiyoruz. Bunu (a + b) nin tam karesinden bulmaya çalışalım.

\displaystyle \text{ }(a+b)=4
\displaystyle \text{ }{{(a+b)}^{2}}=16
\displaystyle {{a}^{2}}+2ab+{{b}^{2}}=16
\displaystyle \underbrace{{{{a}^{2}}+{{b}^{2}}}}_{8}+2ab=16
\displaystyle \text{ }2ab=8
\displaystyle \text{ }ab=4\text{ dir}\text{. Buna g }\!\!\ddot{\mathrm{o}}\!\!\text{ re;}

\displaystyle {{a}^{3}}+{{b}^{3}}=(a+b)\cdot ({{a}^{2}}-ab+{{b}^{2}})
\displaystyle {{a}^{3}}+{{b}^{3}}=(\underbrace{{a+b}}_{4})\cdot (\underbrace{{{{a}^{2}}+{{b}^{2}}}}_{8}-\underbrace{{ab}}_{4})
\displaystyle {{a}^{3}}+{{b}^{3}}=4.(8-4)
\displaystyle {{a}^{3}}+{{b}^{3}}=4.4=16\text{ buluruz}\text{.}

Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 14

İki terimin farkının küpü formülünden yararlanalım.

\displaystyle {{(a-b)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}
Buna göre;
\displaystyle \text{ }{{x}^{3}}-3{{x}^{2}}y=75
\displaystyle \text{ }\underline{{-\text{ }{{y}^{3}}-3x{{y}^{2}}=11\text{ }}}\text{ }
\displaystyle \text{ }{{x}^{3}}-3{{x}^{2}}y+3x{{y}^{2}}-{{y}^{3}}=75-11
\displaystyle \text{ }{{(x-y)}^{3}}=64
\displaystyle \text{ }x-y=4\text{ }buluruz.

Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 13

İki terimin toplamının küpü formülünden yararlanalım.

\displaystyle {{(a+b)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}
Buna göre;
\displaystyle {{(x+1)}^{3}}={{x}^{3}}+3{{x}^{2}}+3x+1\text{ }dir.

Soruda istenen \displaystyle {{x}^{3}}+3{{x}^{2}}+3x-3 idi.
\displaystyle \text{ }{{x}^{3}}+3{{x}^{2}}+3x-3=\underbrace{{{{x}^{3}}+3{{x}^{2}}+3x+1}}_{{}}-4
\displaystyle ={{(x+1)}^{3}}-4\text{ }(x=\sqrt[3]{6}-1\text{ }idi.)
\displaystyle ={{(\sqrt[3]{6}-1+1)}^{3}}-4\text{ }
\displaystyle ={{(\sqrt[3]{6})}^{3}}-4\text{ }
\displaystyle =6-4
\displaystyle =2\text{ }buluruz

Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 12

\displaystyle {{\text{a}}^{2}}+{{c}^{2}}-2{{b}^{2}} ifadesini düzenleyip, iki kare farkından yararlanalım.

\displaystyle {{\text{a}}^{2}}+{{c}^{2}}-2{{b}^{2}}={{\text{a}}^{2}}-{{b}^{2}}+{{c}^{2}}-{{b}^{2}}
\displaystyle \underbrace{{{{\text{a}}^{2}}-{{b}^{2}}}}_{{}}-\underbrace{{({{b}^{2}}-{{c}^{2}})}}_{{}}
\displaystyle \underbrace{{(a-b)}}_{8}(a+b)-\underbrace{{(b-c)}}_{8}(b+c)
\displaystyle 8(a+b)-8(b+c)
\displaystyle 8(a+b-b-c)
\displaystyle 8.(a-c)
\displaystyle \text{ }a-b=8     
\displaystyle \text{ }\underline{{\text{ + }b-c=8\text{ }}}
\displaystyle \text{ }a-c=16
\displaystyle 8.(a-c)=8.16=128\text{ buluruz}\text{.}

Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 11

Bu soruyu çözerken iki kare farkından yararlanalım.

\displaystyle \sqrt{{98.102+4}}=\sqrt{{(100-2).(100+2)+4}}
\displaystyle \text{ }=\sqrt{{{{{100}}^{2}}-{{2}^{2}}+4}}
\displaystyle \text{ }=\sqrt{{{{{100}}^{2}}-4+4}}
\displaystyle \text{ }=\sqrt{{{{{100}}^{2}}}}
\displaystyle \text{ }=100\text{ buluruz}\text{.}

Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 10

İki kare farkından yararlanalım.

\displaystyle \text{ }x-y=24\text{ }\Rightarrow \text{ }\underbrace{{\left( {\sqrt{x}-\sqrt{y}} \right)}}_{4}\cdot \left( {\sqrt{x}+\sqrt{y}} \right)=24
\displaystyle \Rightarrow \sqrt{x}+\sqrt{y}=6\text{ }d\imath r.

\displaystyle \text{ }\sqrt{x}+\sqrt{y}=6
\displaystyle \underline{{+\text{ }\sqrt{x}-\sqrt{y}=4}}
\displaystyle \text{ }2\sqrt{x}=10\text{ }\Rightarrow \text{ }\sqrt{x}=5\text{ }\Rightarrow \text{ }x=25\text{ }dir.

\displaystyle \sqrt{x}+\sqrt{y}=6\text{ }\Rightarrow \text{ }5+\sqrt{y}=6\text{ }\Rightarrow \text{ }y=1\text{ }dir.

Buna göre, \displaystyle x+y=25+1=26 buluruz.

Doğru Cevap: B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 9

İki kare farkı özdeşliğinden yararlanalım.

\displaystyle (Not:\text{ }{{a}^{2}}-{{b}^{2}}=(a-b)(a+b))

\displaystyle {{x}^{2}}-9{{y}^{2}}=36\text{ }\Rightarrow \text{ }{{x}^{2}}-{{(3y)}^{2}}=48
\displaystyle (x-3y)\underbrace{{(x+3y)}}_{{12}}=48
\displaystyle x-3y=4\text{ }bulunur.

\displaystyle \text{ }x+3y=12
\displaystyle \underline{{\text{ }x-3y=4\text{ }}}
\displaystyle \text{ }2x=16
\displaystyle \text{ }x=8\text{ }dir.
Buna göre; 8\displaystyle Buna\text{ }g\ddot{o}re;\text{ }8+3y=12\text{ }\Rightarrow 3y=4\text{ }
\displaystyle \text{ }\Rightarrow y=\frac{4}{3}\text{ }buluruz.

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 8

3 terimli bir ifadenin tam karesini gösteren özdeşlikten yararlanalım.

\displaystyle {{(a+b+c)}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2.(ab+ac+bc)
\displaystyle {{(a+b+c)}^{2}}=\underbrace{{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}_{{11}}+2.(\underbrace{{ab+ac+bc}}_{7})
\displaystyle {{(a+b+c)}^{2}}=11+2.7
\displaystyle {{(a+b+c)}^{2}}=11+14
\displaystyle {{(a+b+c)}^{2}}=25
\displaystyle a+b+c=5\text{ }buluruz.

Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 7

Eşitliğin her iki tarafını 4x’e bölelim.

\displaystyle \frac{{4{{x}^{2}}-7x-4}}{{4x}}=\frac{0}{{4x}}
\displaystyle \frac{{4{{x}^{2}}}}{{4x}}-\frac{{7x}}{{4x}}-\frac{4}{{4x}}=0
\displaystyle x-\frac{7}{4}-\frac{1}{x}=0
\displaystyle x-\frac{1}{x}=\frac{7}{4}\text{ }(Her\text{ }iki\text{ }taraf\imath n\text{ }kare\sin i\text{ alal }\!\!\imath\!\!\text{ m}.)
\displaystyle {{\left( {x-\frac{1}{x}} \right)}^{2}}={{\left( {\frac{7}{4}} \right)}^{2}}
\displaystyle {{x}^{2}}-2\cdot x\cdot \frac{1}{x}+\frac{1}{{{{x}^{2}}}}=\frac{{49}}{{16}}
\displaystyle {{x}^{2}}-2+\frac{1}{{{{x}^{2}}}}=\frac{{49}}{{16}}
\displaystyle {{x}^{2}}+\frac{1}{{{{x}^{2}}}}=\frac{{49}}{{16}}+2
\displaystyle {{x}^{2}}+\frac{1}{{{{x}^{2}}}}=\frac{{49+32}}{{16}}=\frac{{81}}{{16}}\text{ }buluruz.

Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 6

Bu soruda tam kare özdeşliklerinden yararlanalım.

\displaystyle a-\frac{3}{a}=5\text{ }\Rightarrow \text{ }{{\left( {a-\frac{3}{a}} \right)}^{2}}={{(5)}^{2}}
\displaystyle \text{ }{{a}^{2}}-2\cdot a\cdot \frac{3}{a}+{{\left( {\frac{3}{a}} \right)}^{2}}=25
\displaystyle \text{ }{{a}^{2}}-6+\frac{9}{{{{a}^{2}}}}=25
\displaystyle \text{ }{{a}^{2}}+\frac{9}{{{{a}^{2}}}}=31\text{ }dir.

Soruda istenen \displaystyle a+\frac{3}{a} ifadesinin karesini yukarıdaki eşitlikten elde edebiliriz.

\displaystyle a+\frac{3}{a} ‘nın tam karesini yazalım.

\displaystyle {{\left( {a+\frac{3}{a}} \right)}^{2}}={{a}^{2}}+2\cdot a\cdot \frac{3}{a}+\frac{9}{{{{a}^{2}}}}
\displaystyle {{\left( {a+\frac{3}{a}} \right)}^{2}}={{a}^{2}}+6+\frac{9}{{{{a}^{2}}}}
\displaystyle {{\left( {a+\frac{3}{a}} \right)}^{2}}=\underbrace{{{{a}^{2}}+\frac{9}{{{{a}^{2}}}}}}_{{31}}+6
\displaystyle {{\left( {a+\frac{3}{a}} \right)}^{2}}=37
\displaystyle a+\frac{3}{a}=\sqrt{{37}}\text{ }buluruz.

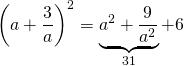
Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 5

(x – y) nin karesini alarak çözüme başlayalım.

\displaystyle (x-y)=3\text{ }\Rightarrow \text{ }{{(x-y)}^{2}}={{3}^{2}}
\displaystyle \text{ }\Rightarrow \text{ }{{x}^{2}}-2xy+{{y}^{2}}=9
\displaystyle \text{ }\Rightarrow \text{ }\underbrace{{{{x}^{2}}+{{y}^{2}}}}_{{29}}-2xy=9
\displaystyle \text{ }\Rightarrow 29-2xy=9
\displaystyle \text{ }2xy=20
\displaystyle \text{ }xy=10\text{ }dur.

Şimdi (x + y) nin karesini hesaplayabiliriz.

\displaystyle {{(x+y)}^{2}}={{x}^{2}}+2xy+{{y}^{2}}=\underbrace{{{{x}^{2}}+{{y}^{2}}}}_{{29}}+2\underbrace{{xy}}_{{10}}
\displaystyle \text{ }=29+2.10=29+20=49
\displaystyle {{(x+y)}^{2}}=49\text{ }\Rightarrow \text{ }x+y=7\text{ }olabilir.

Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 4

Eşitliği taraf tarafa toplarsak, buradan x + y nin karesini elde ederiz.

\displaystyle \text{ }{{x}^{2}}+xy=20
\displaystyle \text{ }\underline{{+\text{ }{{y}^{2}}+xy=5\text{ }}}x 2xy y \displaystyle \text{ }\underbrace{{{{x}^{2}}+2xy+{{y}^{2}}}}_{{}}=25\text{ }\Rightarrow {{(x+y)}^{2}}=25\text{ }ise
\displaystyle x+y=5\text{ }bulunur.

Denklem sisteminde çıkarma yaparsak, buradan iki kare farkı elde ederiz.

\displaystyle \text{ }{{x}^{2}}+xy=20
\displaystyle \underline{{-\text{ }{{y}^{2}}+xy=5\text{ }}}
\displaystyle \text{ }{{x}^{2}}-{{y}^{2}}=15\text{ }\Rightarrow \text{ }(x-y)\underbrace{{(x+y)}}_{5}=15\text{ }tir.

Buradan da \displaystyle x-y=3 bulunur.

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 3

\displaystyle ax+by-ay-bx ifadesini ikili ikili gruplayalım.
\displaystyle \underbrace{{ax-bx}}_{{}}+\underbrace{{by-ay}}_{{}}=x(a-b)-y(a-b)
\displaystyle \text{ }=\underbrace{{(a-b)}}_{5}.\underbrace{{(x-y)}}_{3}
\displaystyle \text{ }=5.3=15\text{ buluruz}\text{.}

Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 2

İfadeyi ikili ikili gruplandırarak çarpanlarına ayırmaya çalışalım.

\displaystyle \underbrace{{{{a}^{6}}-{{a}^{4}}}}_{{}}+\underbrace{{{{a}^{2}}-1}}_{{}}={{a}^{4}}({{a}^{2}}-1)+({{a}^{2}}-1)
\displaystyle \text{ }=({{a}^{2}}-1)({{a}^{4}}+1)\text{ }bulunur.

C şıkkında \displaystyle ({{a}^{4}}+1)\text{ } çarpanı var.

Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 1

\displaystyle {{(x-y)}^{2}}+3(y-x) ifadesini düzenleyip, ortak paranteze almaya çalışalım.

\displaystyle {{(x-y)}^{2}}+3\underbrace{{(y-x)}}_{{-(x-y)}}=(x-y)(x-y)-3(x-y)
\displaystyle \text{ }=(x-y)\left( {x-y-3} \right)

B şıkkında \displaystyle x-y-3 çarpanı vardır.

Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru
Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

“Çarpanlara Ayırma (Latex Formatı)” üzerine 10 yorum

    • Yazım hatası olmuş. 36 olmamalıydı. Şimdi düzeltildi. Bu linkten sayfayı daha düzgün bir şekilde görebilirsiniz.

Yorum yapın