Bu bölümde Belirsizlik Durumları ile ilgili 28 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
Çözüm için Tıklayınız.
2.SORU
| | | | | |
Çözüm için Tıklayınız.
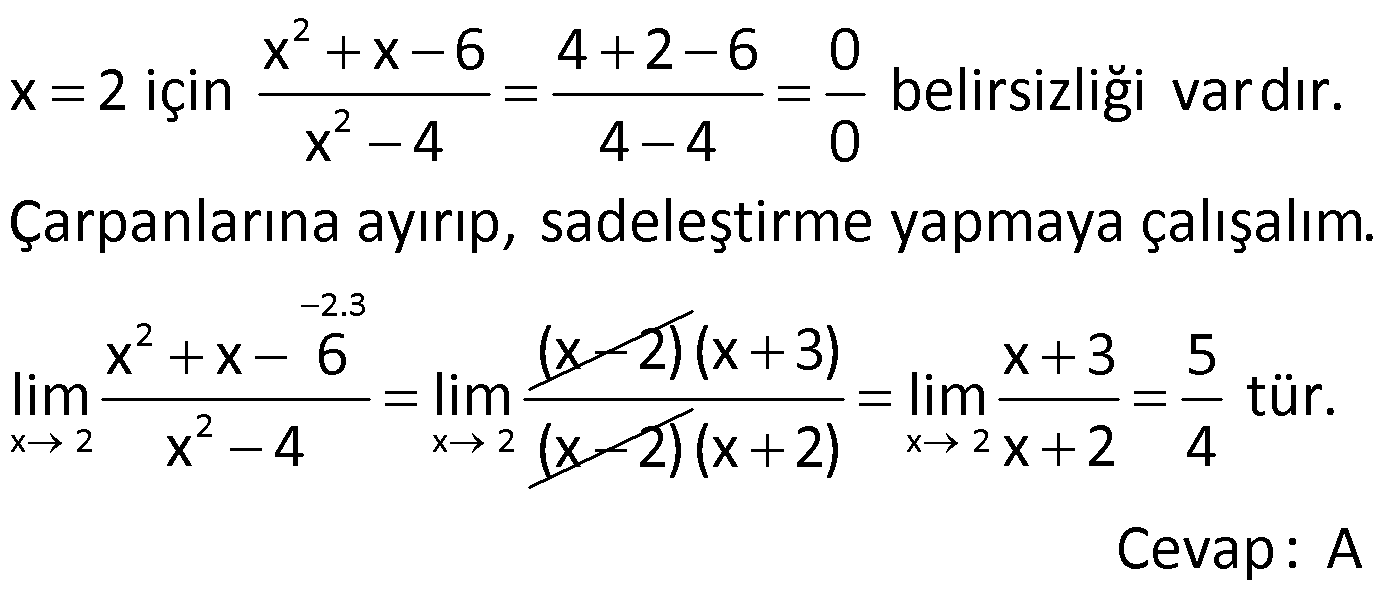
3.SORU
| | | | | |
Çözüm için Tıklayınız.
4.SORU
| | | | | |
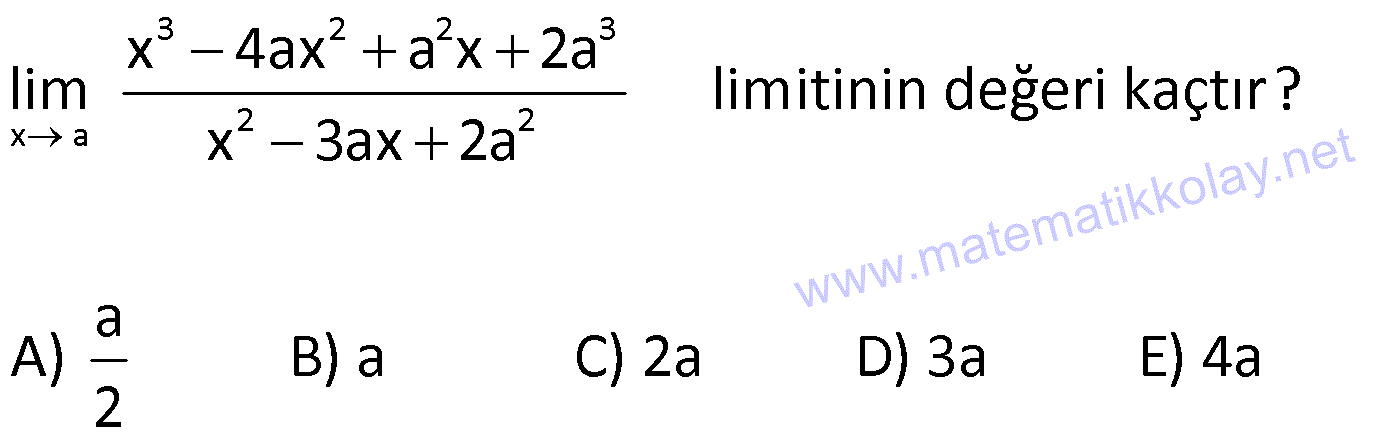
Çözüm için Tıklayınız.
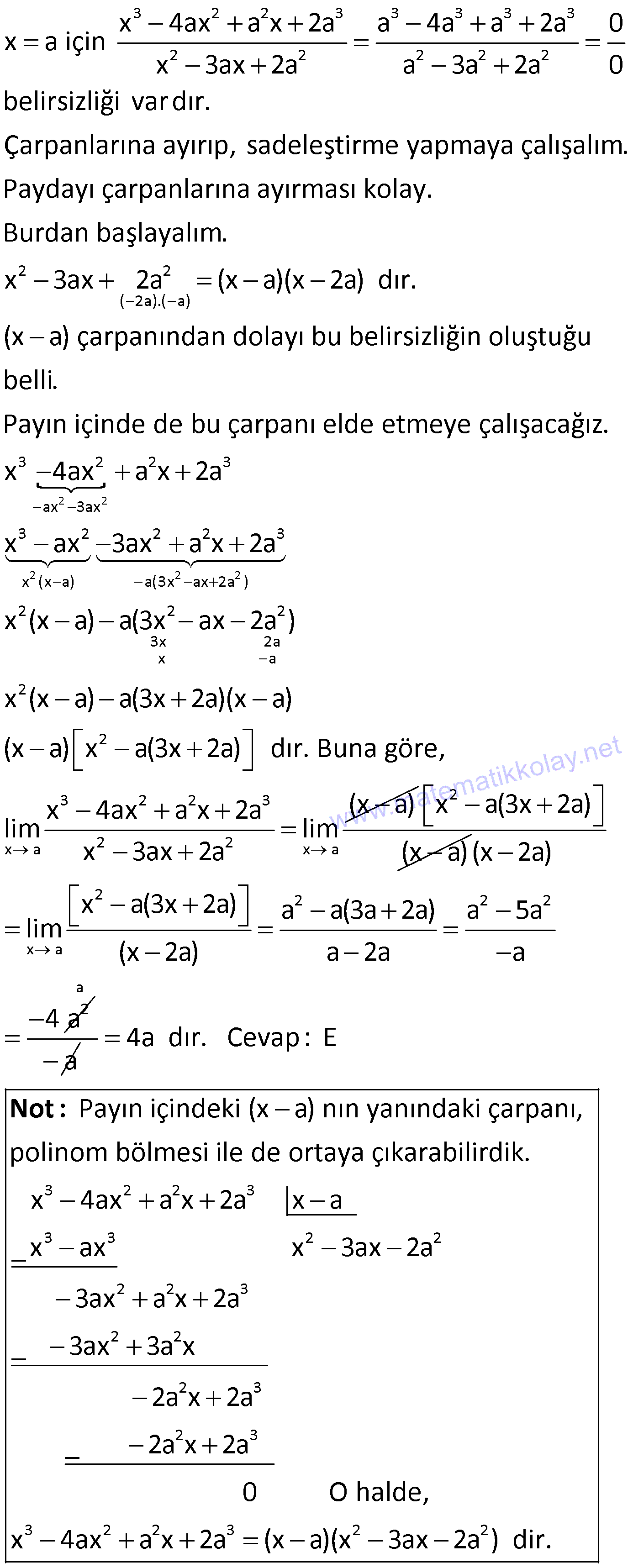
5.SORU
| | | | | |
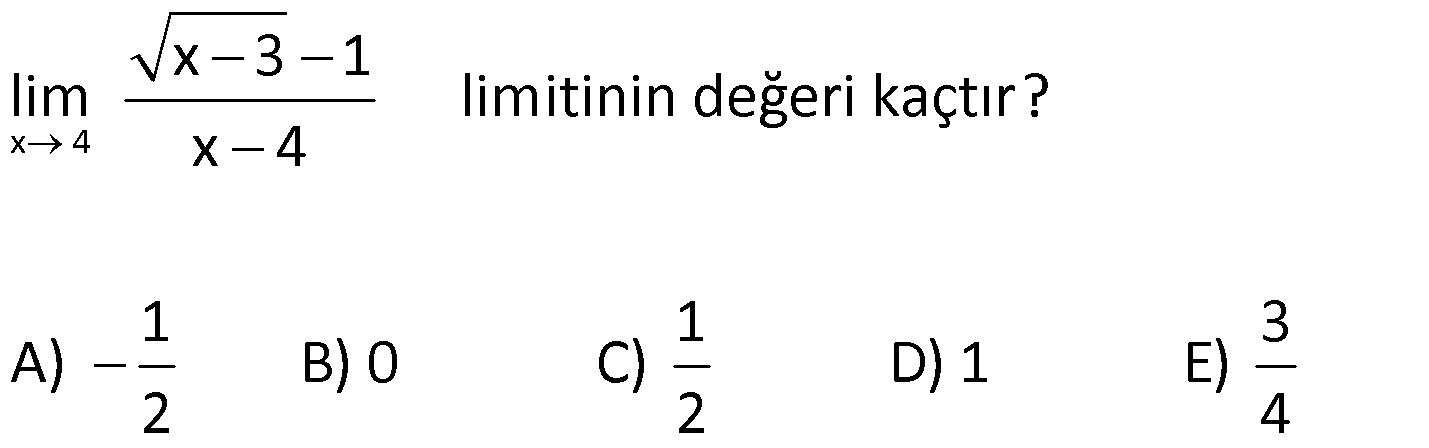
Çözüm için Tıklayınız.
6.SORU
| | | | | |
Çözüm için Tıklayınız.
7.SORU
| | | | | |
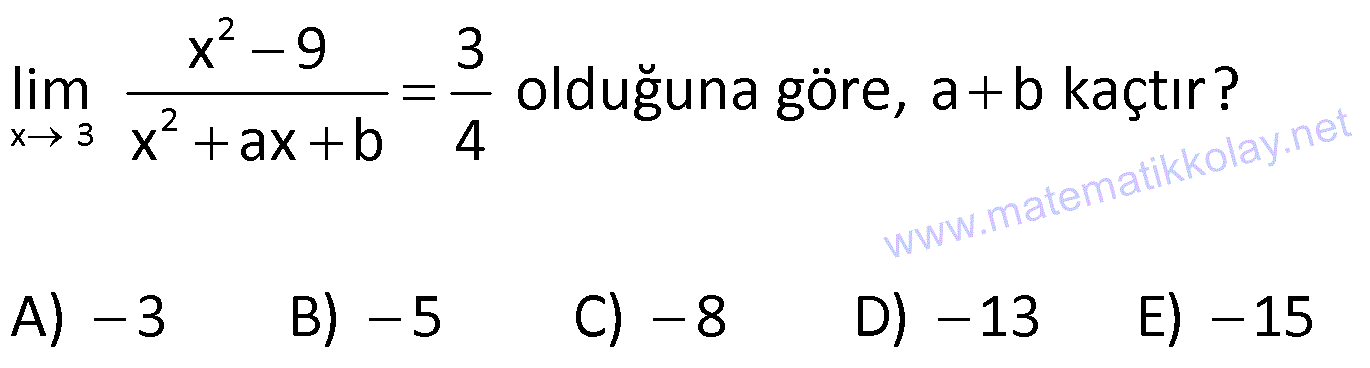
Çözüm için Tıklayınız.
8.SORU
| | | | | |
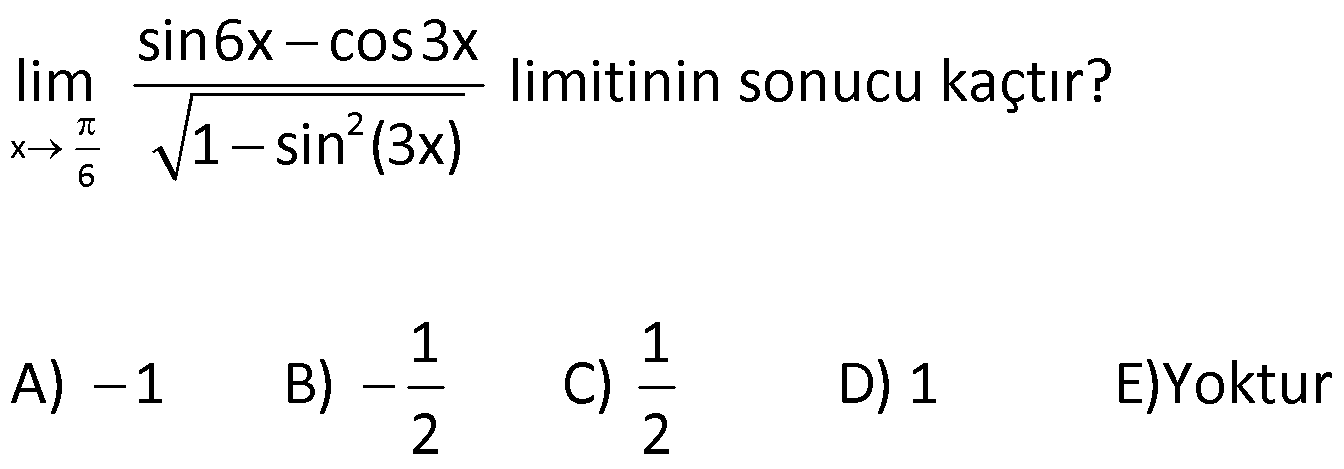
Çözüm için Tıklayınız.
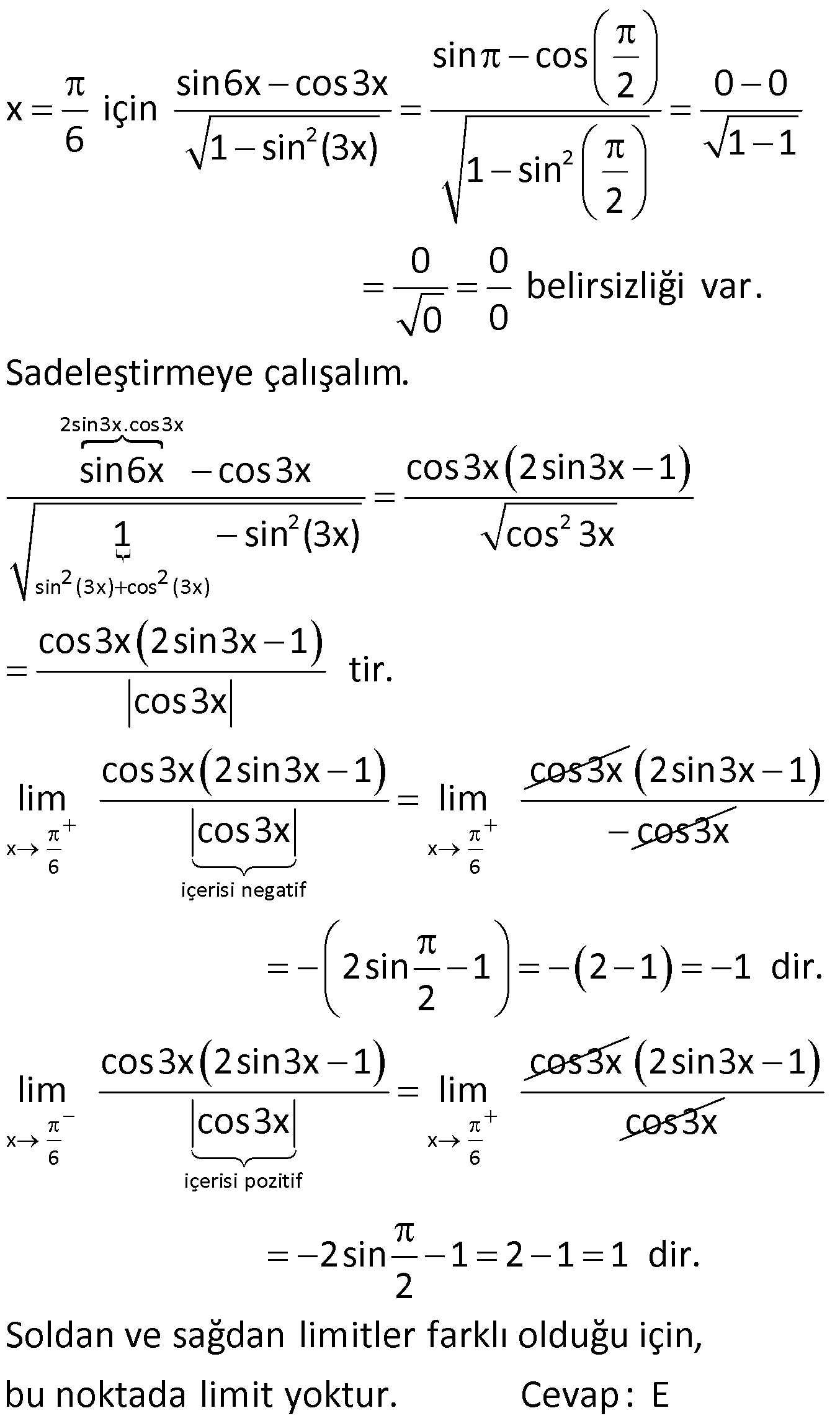
9.SORU
| | | | | |
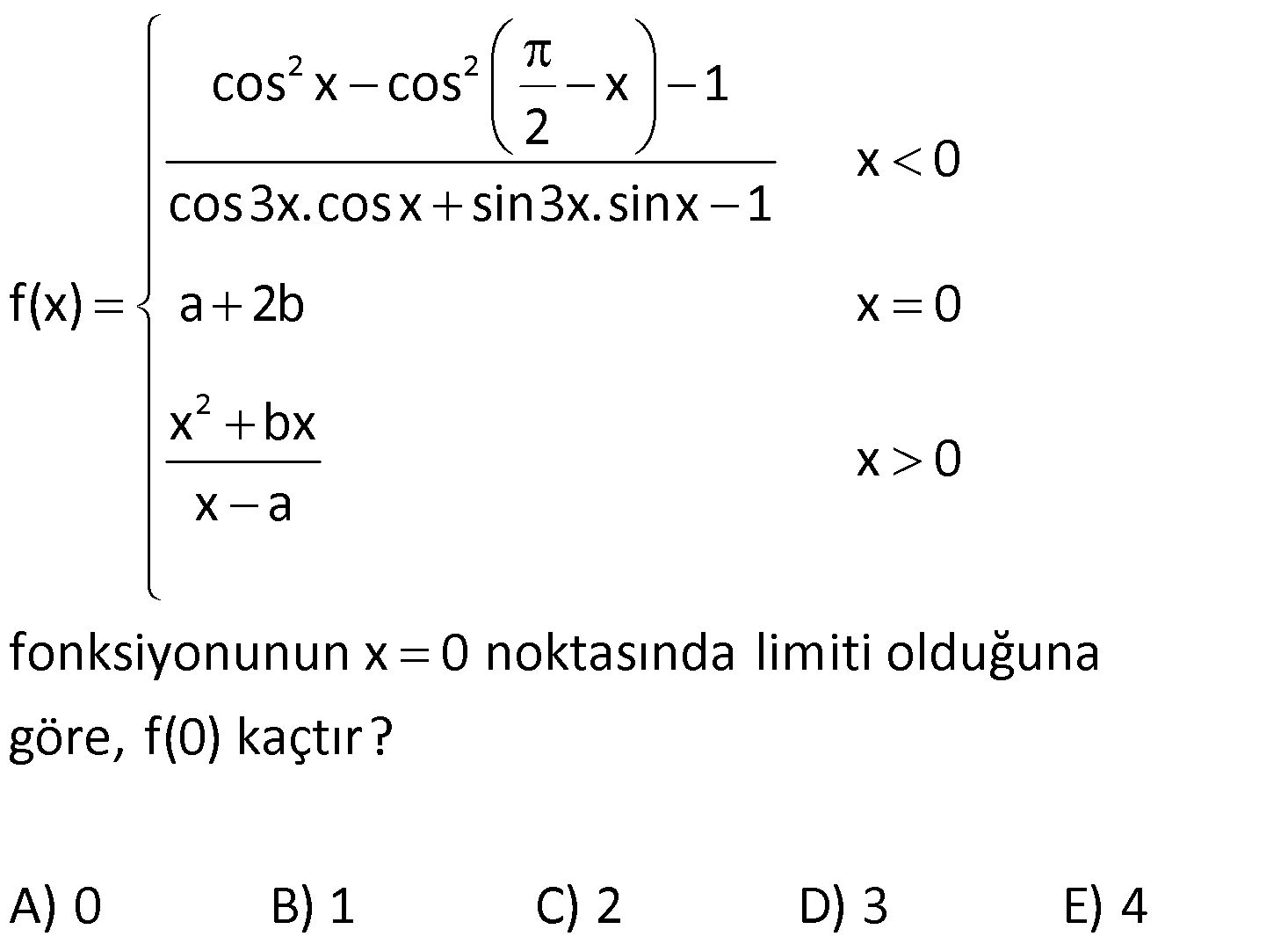
Çözüm için Tıklayınız.
10.SORU
| | | | | |
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
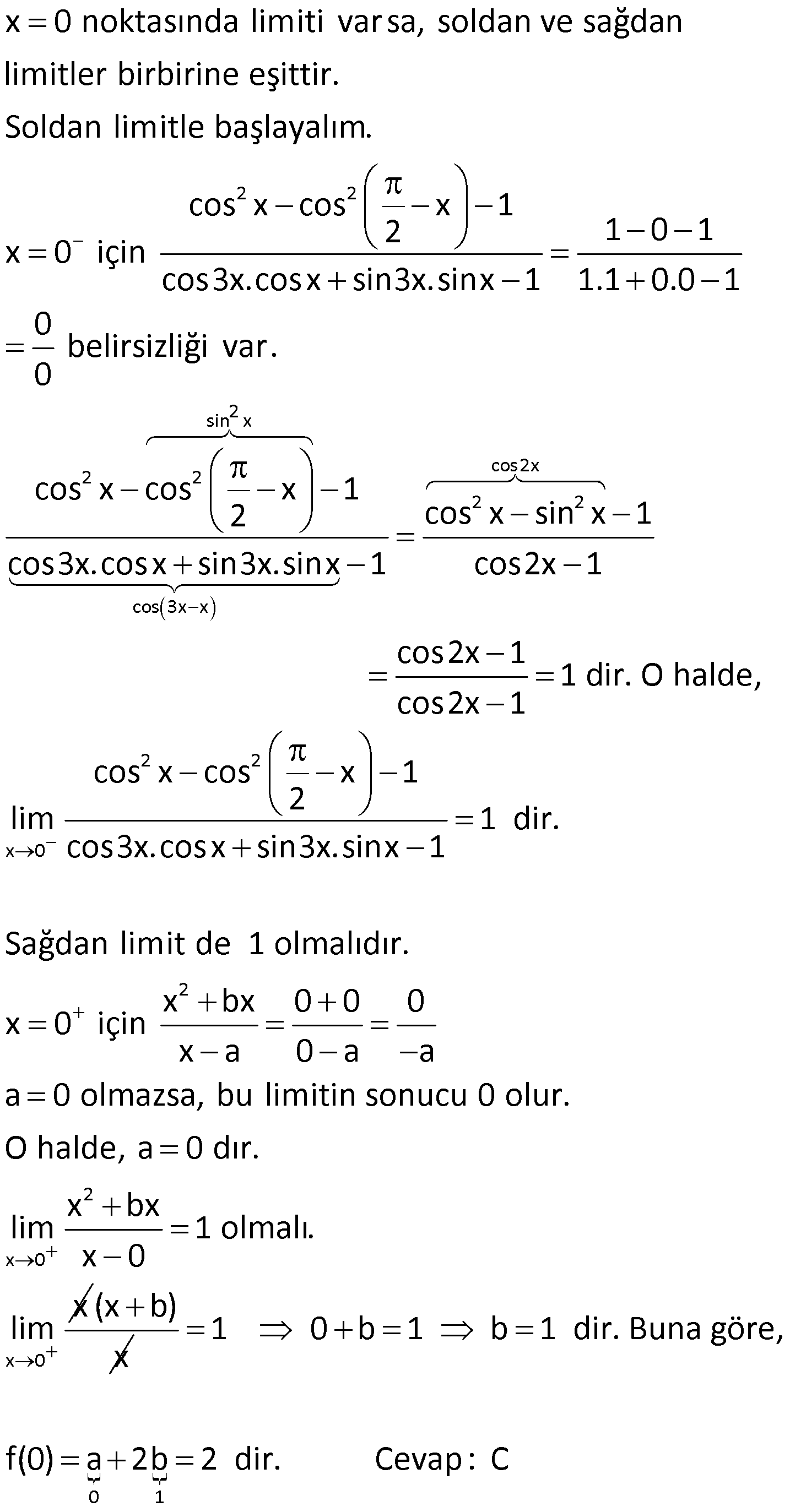
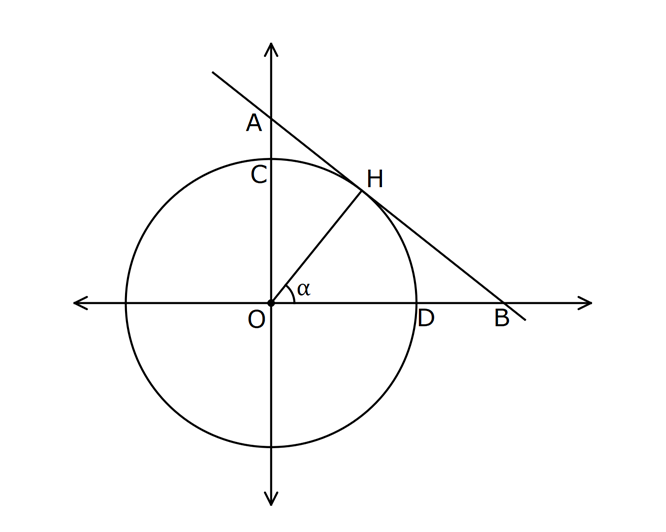
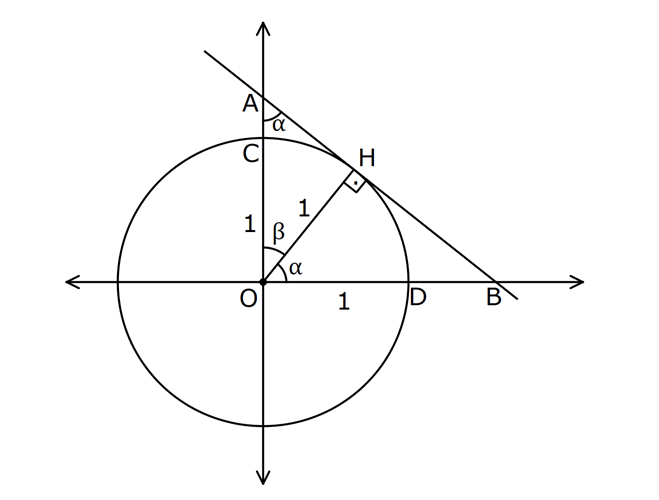
BELİRSİZLİK DURUMLARI www.matematikkolay.net 1) 3 x 4 x 64 lim limitinin değeri kaçtır? x 4 A) 36 B) 48 C) 50 D) 56 E) 64 ÇÖZÜM: x a x a x a 3 lim f(x) 0 ve limg(x) 0 olsun. f(x) 0 lim hesabında belirsizliği ile karşılaşılır. g(x) 0 Bu durumdan kurtulmak için sadeleştirme yapılıp, sonrasında limit hesaplanır. x 64 64 6 x 4 için x 4 Not : 3 x 4 x 4 4 0 belirsizliği vardır. 4 4 0 Çarpanlarına ayırıp, sadeleştirme yapmaya çalışalım. x 64 (x 4) lim lim x 4 2 (x 4x 16) x 4 2 x 4 2 lim (x 4x 16) 4 4.4 16 16 16 16 48 buluruz. Cevap : B 2) 2 2 x 2 x x 6 lim limitinin değeri kaçtır? x 4 5 3 7 12 A) B) C) 2 D) E) 4 2 8 5 ÇÖZÜM: 2 2 2.Mar 2 2 x 2 x 2 x x 6 4 2 6 0 x 2 için belirsizliği vardır. x 4 4 4 0 Çarpanlarına ayırıp, sadeleştirme yapmaya çalışalım. x x 6 (x 2) lim lim x 4 (x 3) (x 2) x 2 x 3 5 lim tür. (x 2) x 2 4 Cevap : A 3) 3 x 1 x 1 lim limitinin değeri kaçtır? x 1 235 A) B) 1 C) D) 2 E) 3 2 3 ÇÖZÜM: 3 6 6 x 1 0 x 1 için belirsizliği vardır. x 1 0 Çarpanlarına ayırıp, sadeleştirme yapmaya çalışalım. x yerine t yazıp, daha rahat işlem yapabiliriz. x 1 iken t 1 dir. t 1 ya da t 1 olabilir. İşlem rahatlığı i 6 3 3 2 x 1 t 1 t 1 3 6 t 1 çin t 1 i kullanalım. Yani x 1 t 1 t 1 lim lim lim x 1 t 1 t 1 (t 1) lim 2 (t t 1) (t 1) 2 t 1 (t 1) (t t 1) lim (t 1) 111 1 1 3 buluruz. Cevap: C 2 4) 3 2 2 3 2 2 x a x 4ax a x 2a lim limitinin değeri kaçtır? x 3ax 2a a A) B) a C) 2a D) 3a E) 4a 2 ÇÖZÜM: www.matematikkolay.net 3 2 2 3 3 3 3 3 2 2 2 2 2 2 2 ( 2 x 4ax a x 2a a 4a a 2a 0 x a için x 3ax 2a a 3a 2a 0 belirsizliği vardır. Çarpanlarına ayırıp, sadeleştirme yapmaya çalışalım. Paydayı çarpanlarına ayırması kolay. Burdan başlayalım. x 3ax 2a 2 2 2 2 2 a).( a) 3 2 2 3 ax 3ax 3 2 2 2 3 x (x a) a(3x ax 2a (x a)(x 2a) dır. (x a) çarpanından dolayı bu belirsizliğin oluştuğu belli. Payın içinde de bu çarpanı elde etmeye çalışacağız. x 4ax a x 2a x ax 3ax a x 2a ) 2 2 2 3x 2a x a 2 2 3 2 2 3 2 2 x a x a x (x a) a(3x ax 2a ) x (x a) a(3x 2a)(x a) (x a) x a(3x 2a) dır. Buna göre, x 4ax a x 2a (x a) lim lim x 3ax 2a 2 x a(3x 2a) (x a) 2 2 2 2 x a 2 (x 2a) x a(3x 2a) a a(3a 2a) a 5a lim (x 2a) a 2a a 4:00 ÖÖ a a 3 2 2 3 3 3 4a dır. Cevap : E Payın içindeki (x a) nın yanındaki çarpanı, polinom bölmesi ile de ortaya çıkarabilirdik. x 4ax a x 2a x a _ x ax Not : 2 2 2 2 3 2 2 2 3 2 3 3 2 2 3 2 x 3ax 2a 3ax a x 2a _ 3ax 3a x 2a x 2a _ 2a x 2a 0 O halde, x 4ax a x 2a (x a)(x 2 3ax 2a ) dir. 5) x 4 x 3 1 lim limitinin değeri kaçtır? x 4 1 1 3 A) B) 0 C) D) 1 E) 2 2 4 ÇÖZÜM: 2 2 x31 x 3 1 1 1 0 x 4 için belirsizliği vardır. x 4 4 4 0 Çarpanlarına ayırmak istiyoruz, ancak ilk etapta yapamıyoruz. Payın eşleniği ile genişletip bir şeyler yakalamaya çalışalım. x 3 1 x 3 1 x 4 (x 4) x 3 x 3 1 1 (x 4) x 3 1 x 4 (x 4) x 4 x 4 1 dir. O halde, x 3 1 x 3 1 x 3 1 1 1 1 lim lim x 4 1 1 x 3 1 4 3 1 1 buluruz. 2 Cevap: C 6) 2 x 2 8x a lim limitinin sonucu gerçek bir sayıya x x 2 eşitse bu limitin değeri kaçtır? 8 4 A) 3 B) C) 2 D) E) 4 3 3 ÇÖZÜM: www.matematikkolay.net 2 2 x 2 x 2 2 1 8x a 16 a 16 a x 2 için dır. x x 2 4 2 2 0 0 Eğer bu kesirde belirsizliği olmazsa, limit gerçek 0 bir sayıya eşit olamaz. Bu sebeple a 16 olmalıdır. 8x 16 8 (x 2) lim lim x x 2 (x 2) x 2 (x 1) 8 lim (x 1) 8 8 buluruz. Cevap: B 3 3 7) 2 2 x 3 x 9 3 lim olduğuna göre, a b kaçtır? x ax b 4 A) 3 B) 5 C) 8 D) 13 E) 15 ÇÖZÜM: 2 x 3 x 9 (x 3)(x 3) tür. Limitin olması için (x 3) çarpanının sadeleşebilmesi gerekiyor. Bu sebeple paydayı (x 3)(x c) şeklinde düşünebiliriz. (x 3) lim I. Yol : (x 3) (x 3) 2 a b 2 2 3 6 3 c 5 tir. (x c) 4 3 c 4 O halde payda (x 3)(x 5) x 2x 15 a b 2 ( 15) 13 buluruz. Cevap: D x 9 9 9 0 x 3 için dir. x ax b 9 3a b 9 3a b Eğer payda 0 olmazsa, bu ifadenin limiti 0’a II.Yol : 2 x 3 9 3a 2 x 3 2 x 3 x 3 eşit olur. O halde paydayı 0’a eşitleyelim. 9 3a b 0 b 9 3a dır. (x 3)(x 3) 3 lim x ax b 4 (x 3)(x 3) 3 lim x ax 9 3a 4 (x 3)(x 3) 3 lim x 9 ax 3a 4 (x 3)(x 3) lim (x 3)(x 3) a(x 3 x 3 3 ) 4 (x 3) lim (x 3) (x 3) 3 (x 3) a 4 6 2 3 6:00 ÖÖ 2 8 6 a a 2 dir. 4 3a b 9 idi. 6 b 9 b 15 tir. O halde, a b 2 ( 15) 13 tür. Cevap : D 8) 2 x 6 sin6x cos3x lim limitinin sonucu kaçtır? 1 sin (3x) 1 1 A) 1 B) C) D) 1 E)Yoktur 2 2 www.matematikkolay.net ÇÖZÜM: 2 2 2 2 2sin3x.cos3x sin (3x) cos (3x) sin cos sin6x cos3x 0 0 2 x için 6 1 sin (3x) 1 1 1 sin 2 0 0 belirsizliği var. 0 0 Sadeleştirmeye çalışalım. sin6x cos3x 1 2 2 x x 6 6 içerisi negatif cos3x 2sin3x 1 sin (3x) cos 3x cos3x 2sin3x 1 tir. cos3x cos3x 2sin3x 1 cos3x lim lim cos3x 2sin3x 1 cos3x x x 6 6 içerisi pozitif 2sin 1 2 1 1 dir. 2 cos3x 2sin3x 1 cos3x lim lim cos3x 2sin3x 1 cos3x 2sin 1 2 1 1 dir. 2 Soldan ve sağdan limitler farklı olduğu için, bu noktada limit yoktur. Cevap : E 9) 2 2 2 cos x cos x 1 2 x 0 cos3x.cosx sin3x.sinx 1 f(x) a 2b x 0 x bx x 0 x a fonksiyonunun x 0 noktasında limiti olduğuna göre, f(0) kaçtır? A) 0 B) 1 C) 2 D) 3 E) 4 ÇÖZÜM: 2 2 2 2 x 0 noktasında limiti varsa, soldan ve sağdan limitler birbirine eşittir. Soldan limitle başlayalım. cos x cos x 1 2 1 0 1 x 0 için cos3x.cosx sin3x.sinx 1 1.1 0.0 1 0 belirsizliği var. 0 cos x cos 2 sin x cos2x 2 2 cos 3x x 2 2 x 0 x 1 2 cos x sin x 1 cos3x.cosx sin3x.sinx 1 cos2x 1 cos2x 1 1 dir. O halde, cos2x 1 cos x cos x 2 lim 2 2 x 0 x 0 1 1 dir. cos3x.cosx sin3x.sinx 1 Sağdan limit de 1 olmalıdır. x bx 0 0 0 x 0 için x a 0 a a a 0 olmazsa, bu limitin sonucu 0 olur. O halde, a 0 dır. x bx lim 1 olmalı. x 0 x lim (x b) x 0 1 1 0 b 1 b 1 dir. Buna göre, f(0) a 2b 2 dir. Cevap : C 10) www.matematikkolay.net 2 Yukarıda verilen grafikte, AB doğrusu H noktasında birim çembere teğettir. m(BOH) olduğuna göre, lim AC . DB . OB limitinin değeri kaçtır? 1 1 2 4 A) B) C) 1 D) E) 2 2 3 3 ÇÖZÜM: İlk önce, uzunlukları ya bağlı olarak ifade etmeye çalışalım. m(AOH) olsun. 90 olur. Birim çemberin yarıçapı 1 br dir, zaten. 1 Buna göre, AOH üçgeninde sin dur. AO 1 O halde, AO dir. Dolay sin 2 1 ısıyla AC 1 sin olur. Merkezden teğete çizilen doğru dik açı yapacağı için [OH] [AB] dir. 1 HOB üçgeninde cos dir. Yani, OB 1 1 OB dir. Dolayısıyla DB 1 dır. cos cos Buna göre, limiti bulalım. lim 2 2 2 2 1 1 1 AC . DB . OB lim 1 1 sin cos cos 1 sin 1 cos 1 lim sin cos cos (1 sin )(1 cos ) lim sin .cos 2 2 2 (1 sin )(1 cos ) lim sin .(1 sin ) (1 sin ) lim (1 cos ) sin . (1 sin ) 2 (1 sin ) (1 cos ) lim sin .(1 sin ) 1 0 1 buluruz. Cevap: B 1.(1 1) 2
