Belirsiz İntegral ve Temel İntegral Alma Kuralları

2.Sayfa için Tıklayınız.

21.SORU

Çözüm için Tıklayınız.

22.SORU


Çözüm için Tıklayınız.

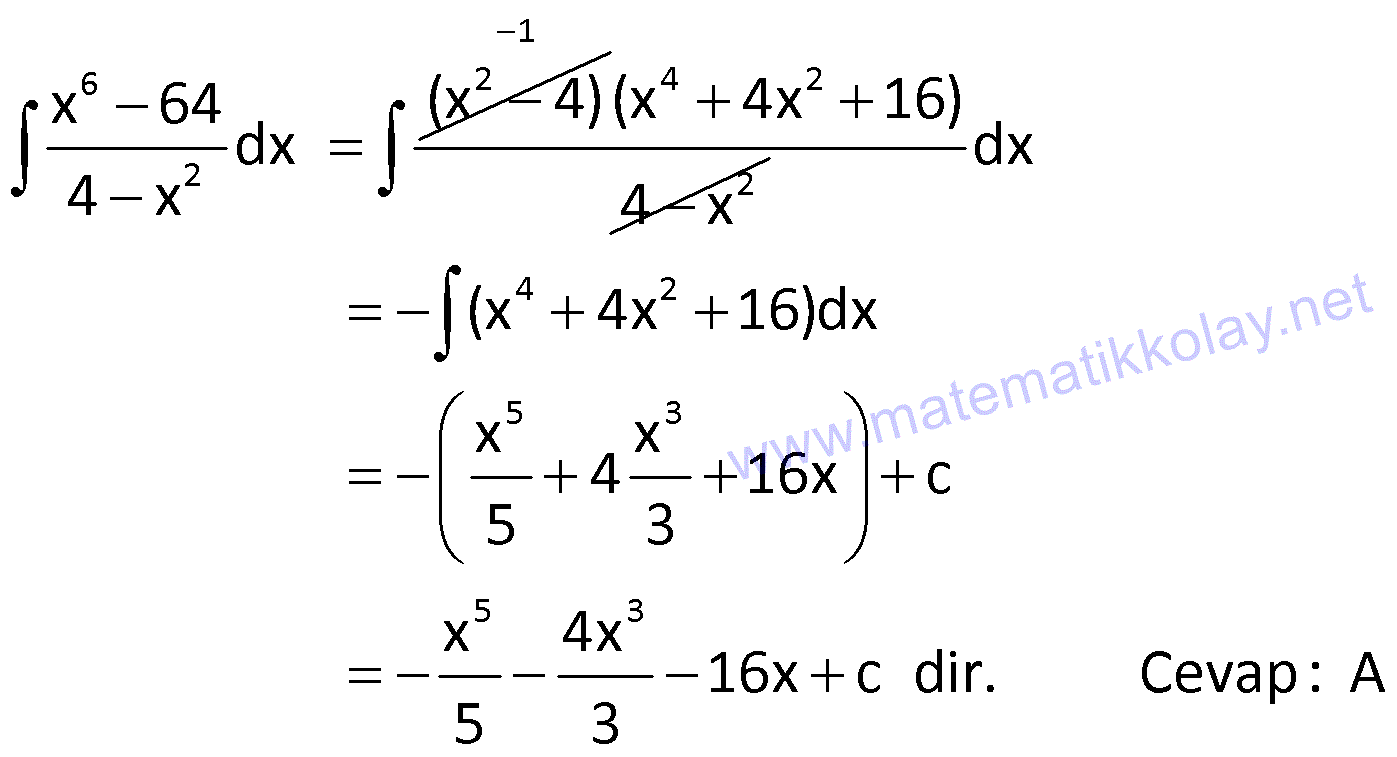
23.SORU

Çözüm için Tıklayınız.

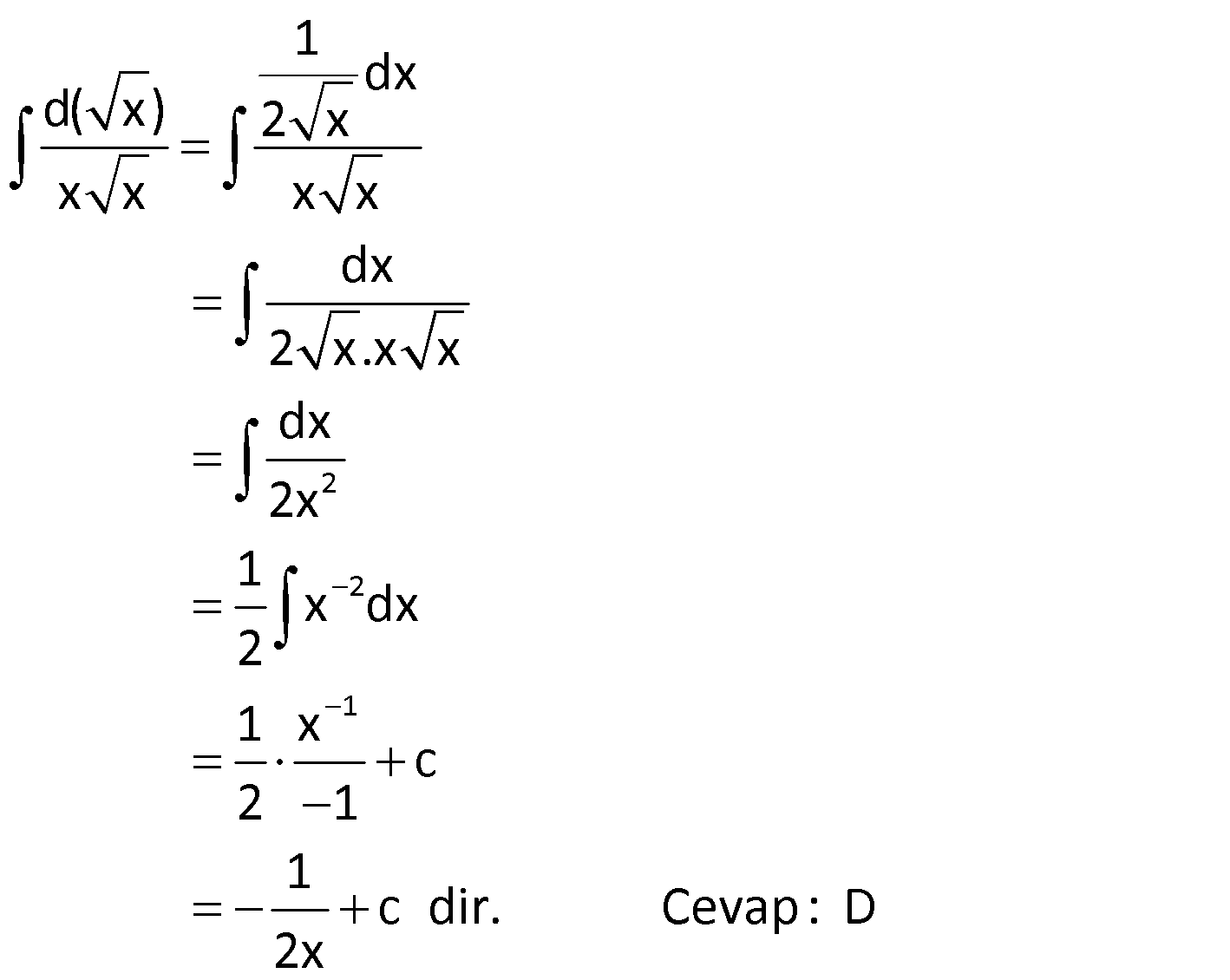
24.SORU

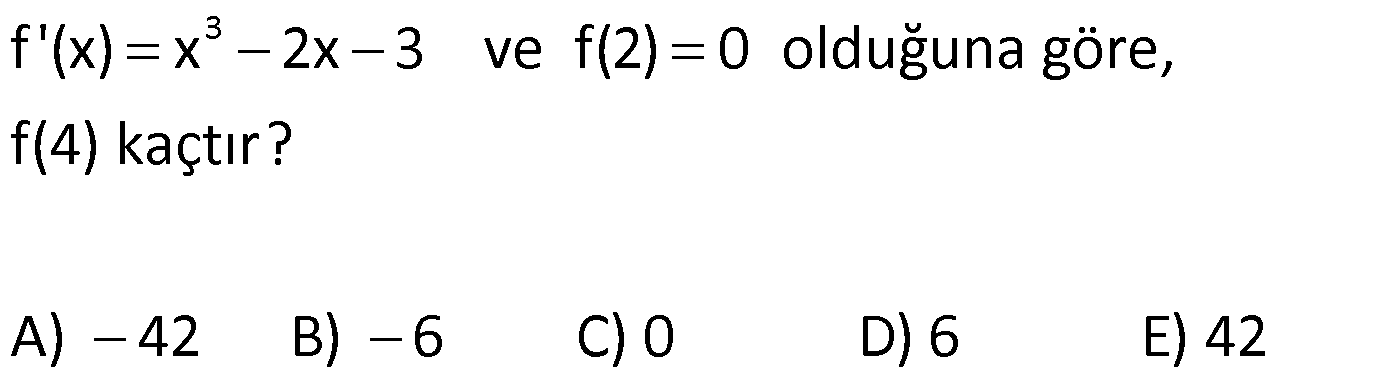
Çözüm için Tıklayınız.

25.SORU

Çözüm için Tıklayınız.

26.SORU

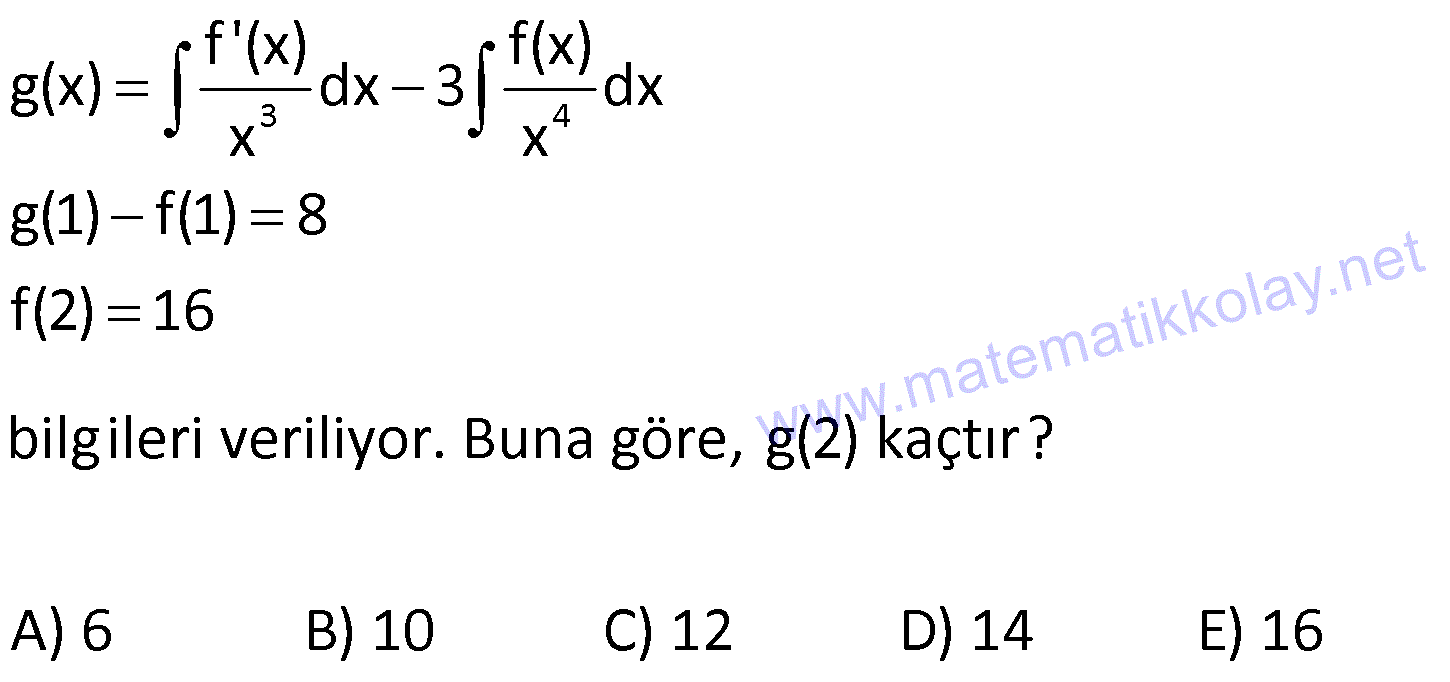
Çözüm için Tıklayınız.

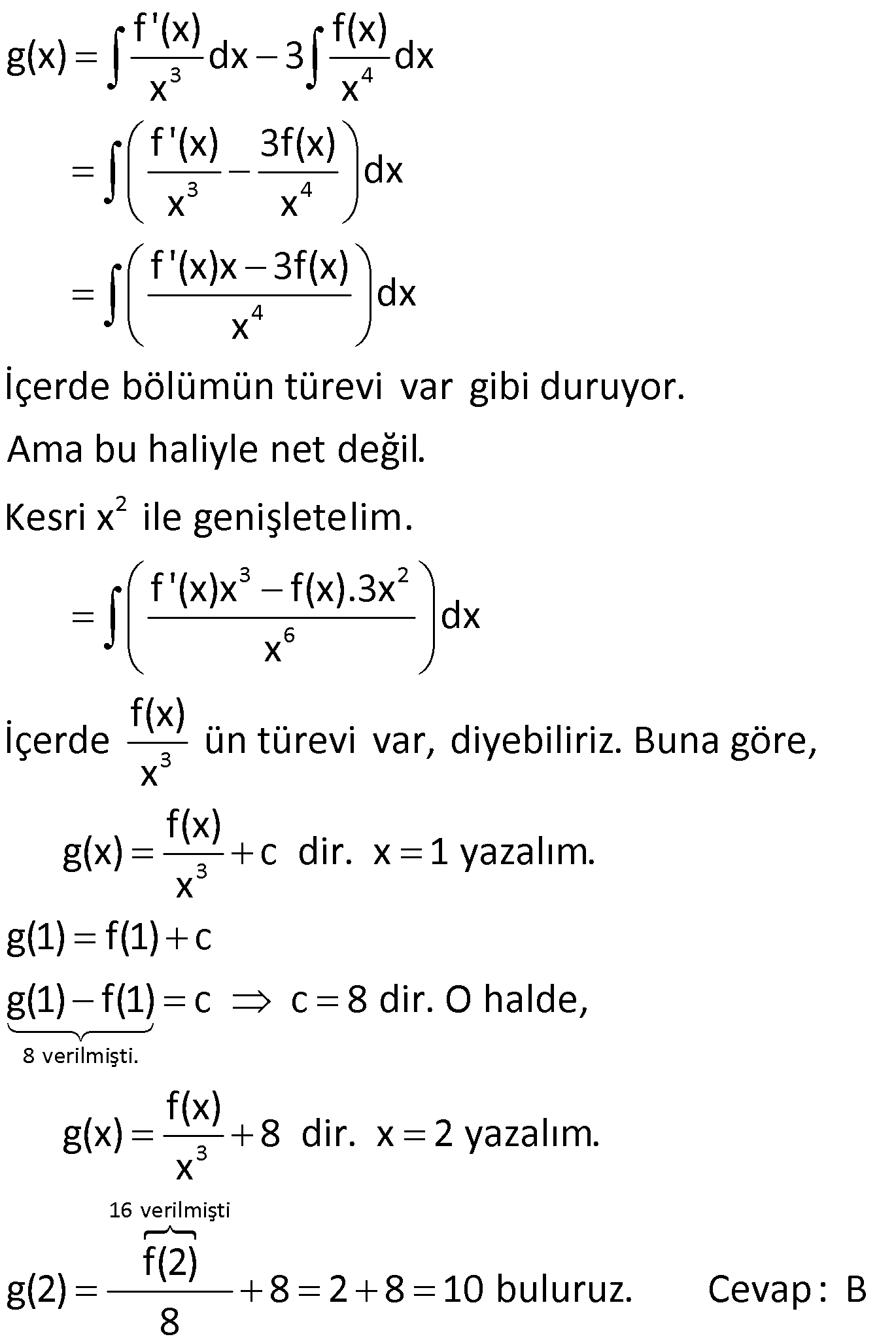
27.SORU

Çözüm için Tıklayınız.

28.SORU

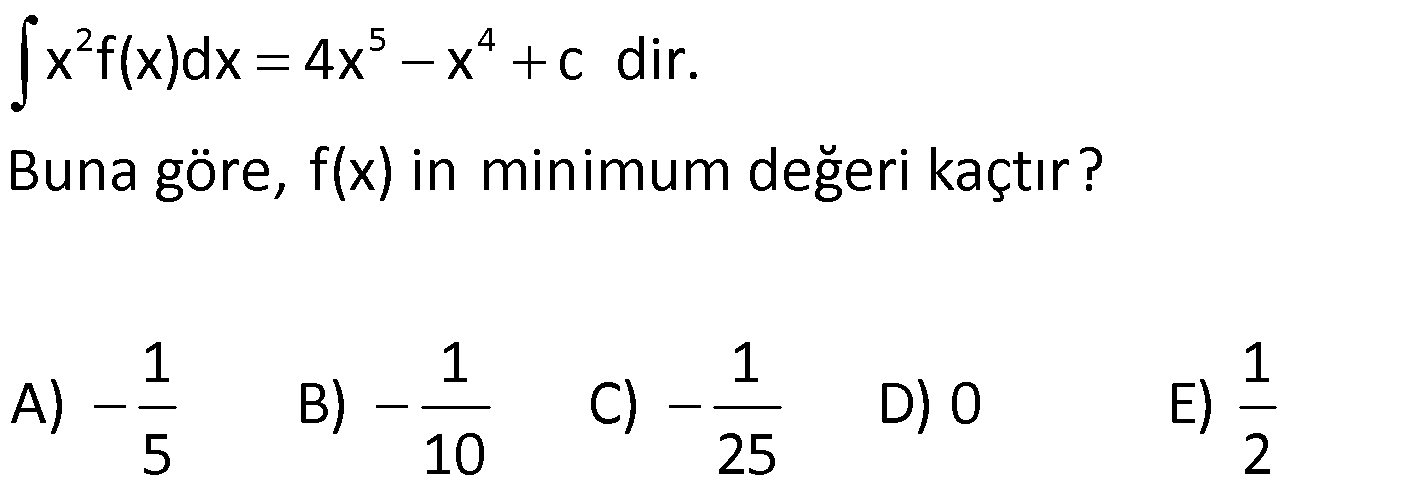
Çözüm için Tıklayınız.

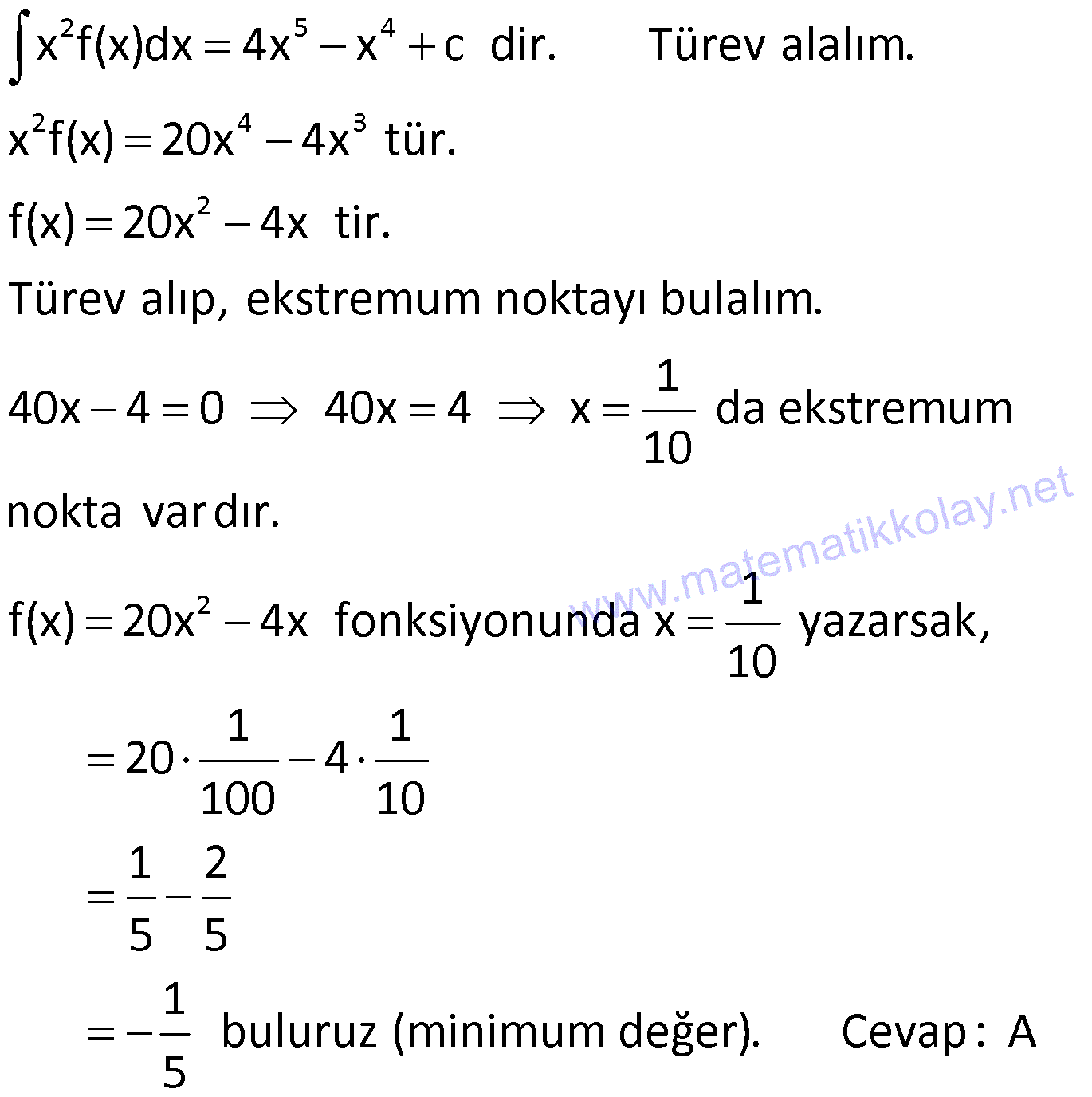
29.SORU

Çözüm için Tıklayınız.

Sorular Bitti. Diğer Çözümlü Testler için Tıklayabilirsiniz.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.) 21) 2 2 2 2 3 2 2 3 2 2 4 3 xy xy dy integralinin sonucu aşağıdakilerden hangisidir? x y x y xy xy A) c B) c 2 2 3 2 x y x y C) c D) 2xy x c 6 4 (xy) (xy) E) c 4 3 ÇÖZÜM: 2 2 3 2 3 2 dy den dolayı y ye göre integral alacağız. Dolayısıyla x, bir katsayı gibi işlem görür. xy xy dy x (y y)dy y y x c dir. 3 2 xy xy c di 3 2 r. Cevap : B 22) www.matematikkolay.net 6 2 7 5 3 3 5 3 4 7 x 64 dx integralinin sonucu aşağıdakilerden 4 x hangisidir? x 64x x 4x 7 A) 16x c B) c 5 3 x 4x 3 x 8x C) 3x c D) 16x c 5 3 x E) 64x c 7 ÇÖZÜM: 6 2 2 x 64 (x 4) dx 4 x 1 4 2 2 (x 4x 16) 4 x 4 2 5 3 5 3 dx (x 4x 16)dx x x 4 16x c 5 3 x 4x 16x c dir. Cevap : A 5 3 23) 2 d( x) integralinin sonucu aşağıdakilerden x x hangisidir? x 2 A) c B) 2x c C) c 2 x 1 D) c E) x c 2x ÇÖZÜM: 2 2 1 1 dx d( x) 2 x x x x x dx 2 x.x x dx 2x 1 x dx 2 1 x c 2 1 1 c dir. Cevap: D 2x 24) 3 f'(x) x 2x 3 ve f(2) 0 olduğuna göre, f(4) kaçtır? A) 42 B) 6 C) 0 D) 6 E) 42 ÇÖZÜM: 4 2 4 2 İntegral alarak f(x) i elde edelim. x f(x) x 3x c dir. 4 f(2) 0 ı kullanarak c yi bulalım. 16 0 4 6 c 4 0 4 4 6 c 0 6 c c 6 dır. O halde, x f(x) x 3x 6 dır. Şimdi f(4) ü bulabiliriz. 4 256 f(4) 16 12 6 4 64 16 12 6 70 28 42 buluruz. Cevap : E 25) f”(x) 12x 6 f'(3) 41 f(2) 13 bilgileri veriliyor. Buna göre, f(1) kaçtır? A) 3 B) 4 C) 5 D) 6 E) 7 www.matematikkolay.net ÇÖZÜM: 2 2 2 2 f”(x) 12x 6 her iki tarafın integralini alalım. x f'(x) 12 6x c 2 6x 6x c f'(3) 41 eşitliğini kullanalım. 41 6.3 6.3 c 41 54 18 c 41 36 c c 5 tir. O halde, f'(x) 6x 6x 5 tir. Tek 3 2 3 2 3 2 3 2 rar integral alalım. x x f(x) 6 6 5x c 3 2 f(x) 2x 3x 5x c dir. f(2) 13 eşitliğini kullanalım. 13 2.2 3.2 5.2 c 13 16 12 10 c 13 14 c c 1 dir. O halde, f(x) 2x 3x 5x 1 dir. Buna göre , f(1) 2 3 5 1 3 tür. Cevap : A 26) 3 4 f'(x) f(x) g(x) dx 3 dx x x g(1) f(1) 8 f(2) 16 bilgileri veriliyor. Buna göre, g(2) kaçtır? A) 6 B) 10 C) 12 D) 14 E) 16 ÇÖZÜM: 3 4 3 4 4 2 3 2 f'(x) f(x) g(x) dx 3 dx x x f'(x) 3f(x) dx x x f'(x)x 3f(x) dx x İçerde bölümün türevi var gibi duruyor. Ama bu haliyle net değil. Kesri x ile genişletelim. f'(x)x f(x).3x 6 3 3 8 verilmişti. 3 dx x f(x) İçerde ün türevi var, diyebiliriz. Buna göre, x f(x) g(x) c dir. x 1 yazalım. x g(1) f(1) c g(1) f(1) c c 8 dir. O halde, f(x) g(x) 8 dir. x 2 yazalım x 16 verilmişti . f(2) g(2) 8 2 8 10 buluruz. Cevap : B 8 27) f(x) fonksiyonunun ( 1, 3) noktasındaki teğetinin eğimi 4 tür. f”(x) 24x 8 olduğuna göre, f(2) kaçtır? A) 32 B) 25 C) 21 D) 15 E) 8 ÇÖZÜM: www.matematikkolay.net 2 2 2 f”(x) 24x 8 her iki tarafın integralini alalım. x f'(x) 24 8x c 2 12x 8x c f'( 1) 4 eşitliğini kullanalım (teğetin eğimi). 4 12 8 c 4 20 c c 16 dır. O halde, f'(x) 12x 8x 16 dir. 3 2 3 2 3 2 Tekrar integral alalım. x x f(x) 12 8 16x c 3 2 f(x) 4x 4x 16x c dir. ( 1, 3) noktasını kullanalım. 3 4 4 16 c 3 8 c c 5 tir. O halde, f(x) 4x 4x 16x 5 tir. Buna göre, f(2) 4.8 4.4 32 5 32 16 32 5 21 dir. Cevap: C 28) 2 5 4 x f(x)dx 4x x c dir. Buna göre, f(x) in minimum değeri kaçtır? 1 1 1 1 A) B) C) D) 0 E) 5 10 25 2 ÇÖZÜM: 2 5 4 2 4 3 2 2 x f(x)dx 4x x c dir. Türev alalım. x f(x) 20x 4x tür. f(x) 20x 4x tir. Türev alıp, ekstremum noktayı bulalım. 1 40x 4 0 40x 4 x da ekstremum 10 nokta vardır. f(x) 20x 4x fonksi 1 yonunda x yazarsak, 10 1 1 20 4 100 10 1 2 5 5 1 buluruz (minimum değer). Cevap : A 5 29) 3 2 3 P(x) bir polinom olmak üzere, x .P”(x) in derecesi 8 dir. Buna göre, P (x )dx in derecesi kaçtır? A) 14 B) 26 C) 43 D) 48 E) 54 ÇÖZÜM: 3 2 3 2.3.a Polinomlarda her türev, dereceyi bir azaltırken integral bir artırır. P(x) in derecesi a olsun. der[x .P”(x)] 8 ise 3 (a 2) 8 dir. a 1 8 a 7 dir. Buna göre, der P (x )dx 6 Not : integral a 1 6.7 1 42 1 43 tür. Cevap: C
Sayfalar: 1 2 3

“Belirsiz İntegral ve Temel İntegral Alma Kuralları” üzerine 6 yorum

  3. Admin olmayan AdminBey, benim yerime cevap vermiş :))

    İşin doğrusu şu,
    Maalesef, dolaylı yollardan da olsa, koronadan işler aksıyor.
    Ben korona olmasam da, olan biri nedeniyle iş yoğunluğum başka yöne kayıyor.
    Bu sebeple gecikmeler yaşanıyor.

    Bu aralar, integralin ilk kısmı ile ilgili sorular hazırlanıyor. Yakında ilk yüklemesi yapılacak.

Yorum yapın