Bu bölümde Belirsiz İntegral ve Temel İntegral Alma Kuralları ile ilgili 29 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
BELİRSİZ İNTEGRAL VE TEMEL İNTEGRAL ALMA KURALLARI www.matematikkolay.net 1) 2 3 3 2 2 Reel sayılarda tanımlı f(x) fonksiyonunun türevi f'(x) 3x 4 olduğuna göre, f(x) aşağıdakilerden hangisi olabilir? A) 6x 4 B) x 4x 2 C) x 4 D) 3x 4x E) 3x 4x 5 ÇÖZÜM: 2 3 3 3x ifadesi x ün türevidir. 4 ifadesi 4x in türevidir. Bir de bunların yanında sabit terim (c) varsa, onun da türevi 0 gelmiştir. Yani, f(x) x 4x c şeklinde bir fonksiyondur. O halde f(x) fonksiyonu, B şıkkındaki gibi bir ifade olabilir. Cevap: B Türevi belli olan bir fonksiyonun kendisini bulma işlemine integral alma işlemi Not : 2 3 Türevin integral Türev x e göre sabiti alındığını (Değerini anlıyoruz. bilmiyoruz denir. (Biz buna türevin tersi de diyebiliriz.) işareti de integral sembolüdür. (3x 4) dx x 4x c ) dir. 2) 2 2 2 3 3 2 f(x) x 2x ve g(t) t fonksiyonlarının diferansiyelleri aşağıdakilerden hangisinde doğru verilmiştir? f(x) in diferansiyeli g(t) nin diferansiyeli A) 2x 2 t x t B) x c c 3 3 C) ( 3 3 2 2x 2)dx 2tdt x t D) x c dx c dt 3 3 E) 2xdx 2tdt ÇÖZÜM: y f(x) fonksiyonunun türevini dy f'(x) olarak gösterebiliyorduk. dx d(f(x)) veya f'(x) olarak yazabiliriz. dx dx i karşıya atarsak d(f(x)) f'(x).dx olur. İşte bu ifad Not : Türev f(x) in türevi değişkeni Türev f(x) in türevi değişkeni eye f(x) in denir. Buna göre, f(x) in diferansiyeli d(f(x)) (2x 2) . dx tir. g(t) nin diferansiyeli d(g(t)) (2t) . dt t diferansiyeli ir. Cevap : C 3) d(f(x)) (2x 1)dx ise f(2) f(1) kaçtır? A) 4 B) 5 C) 6 D) 7 E) 8 ÇÖZÜM: 2 d(f(x)) (2x 1)dx ise f'(x) 2x 1 dir. Ters türevini (integralini) alalım. f(x) x x c olur. f(2) f(1) (4 2 c) (1 1 c) 6 c 2 c 4 tür. Cevap: A 4) 2 2 2 3 d(f(x)) dx ise f”(x) aşağıdakilerden hangisidir? x 2 A) x 2 B) 2x C) x D) 2x 2 E) x 2x ÇÖZÜM: f'(x) dx 2 dx x 2 2 f'(x) x 2 Tekrar türev alalım. f”(x) 2x tir. Cevap: B www.matematikkolay.net 5) 2 2 3 3 2 (3x 5)dx integralinin sonucu aşağıdakilerden hangisidir? A) x x c B) x x c C) 6x 5 c D) x 5x c E) 3x 5 c ÇÖZÜM: 2 3 2 2 (3x 5)dx içerdeki ifadenin integralini yani ters türevini alacağız. x ün türevi 3x dir. 5 in türevi 5x tir. Bir de bunların yanında sabit terim (c) varsa, onun türevi 0 gelmiştir. Yani, (3x 5)dx 3 x 5x c dir. Cevap : D “c” integral sabitinin değerini bilmediğimiz için bu integral işlemine denir. Not : Belirsiz İntegral 6) 2 2 3 t tdt c 2 dx x c 3t dx t c Yukarıda verilen integrallerin sonuçlarından hangileri doğrudur? A) I ve II B) I ve III C) II ve III D) Yalnız II E) I, II v I. II. III. e III ÇÖZÜM: 2 t ye göre türev alınmış. 2 x e göre türev alınmış. Sırayla öncülleri inceleyelim. t t. dt c dir. 2 t 2t Çünkü c nin t ye göre türevi t dir. Doğru. 2 2 dx 1. dx x c dir. Çünkü x c nin x e göre tür I. II. 2 2 x e göre türev alınmış. 2 2 2 3 evi 1 dir. Doğru. 3t . dx 3t x c olmalıydı. 3t ifadesi x için sabit bir katsayı gibidir. Değişken değildir. 3t x c nin x e göre türevi 3t dir. t c nin x’e göre türevi ise 0 III. dır. Cevap : A 7) 2 3 a ve b birer reel sayı olmak üzere, (3x ax b)dx x 5x 2x c olduğuna göre, a b kaçtır? A) 7 B) 5 C) 3 D) 3 E) 7 ÇÖZÜM: integrali Türevi 3 2 3 2 2 2 2 0 7 dx x 5x 2x c ifadesinin türevi 3x ax b ye eşit olmalıdır. x 5x 2x c ‘ 3x 5 2 0 3x 7 dir. 3x ax b 3x 7 ise a b 0 7 Not : 7 dir. Cevap :E www.matematikkolay.net 8) d f(x) (x x)dx olduğuna göre, f(4) kaçtır? dx A) 2 B) 4 C) 6 D) 8 E) 10 ÇÖZÜM: d f(x)dx f(x) tir. dx Bir fonksiyonun integralinin türevi, yine fonksiyonun kendisine eşittir. Buna göre, d (x x)dx x x tir. dx f(4) 4 4 4 2 2 dir. Cevap : A Not : 9) d 2 3 f(x) x (t t)dt olduğuna göre, f(2) kaçtır? dx A) 2 B) 4 C) 6 D) 8 E) 10 ÇÖZÜM: 2 3 2 3 x e göre sabit bir değerdir. d f(x) x (t t)dt dx d d x (t t)dt dx dx 2x 0 dır. 2x tir. f(2) 2.2 4 tür. Cevap: B 10) 2 5 3 x f(x)dx x x c olduğuna göre, f(x) in x 2 noktasındaki teğetinin eğimi kaçtır? A) 12 B) 16 C) 18 D) 20 E) 28 ÇÖZÜM: 2 5 3 2 4 2 4 2 2 2 x f(x)dx x x c İki tarafın da türevini alalım. x f(x) 5x 3x olur. 5x 3x f(x) x f(x) 5x 3 tür. f'(x) 10x tir. f'(2) 20 dir. (x 2 noktasındaki teğetinin eğimi) Cevap: D
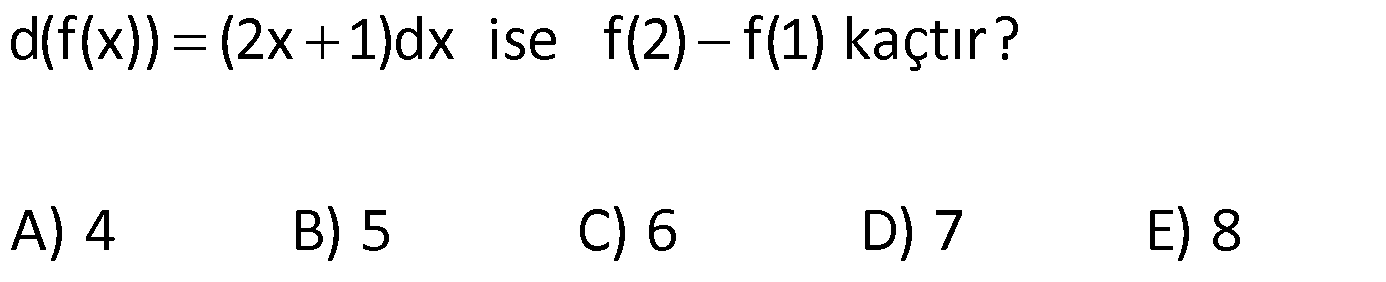
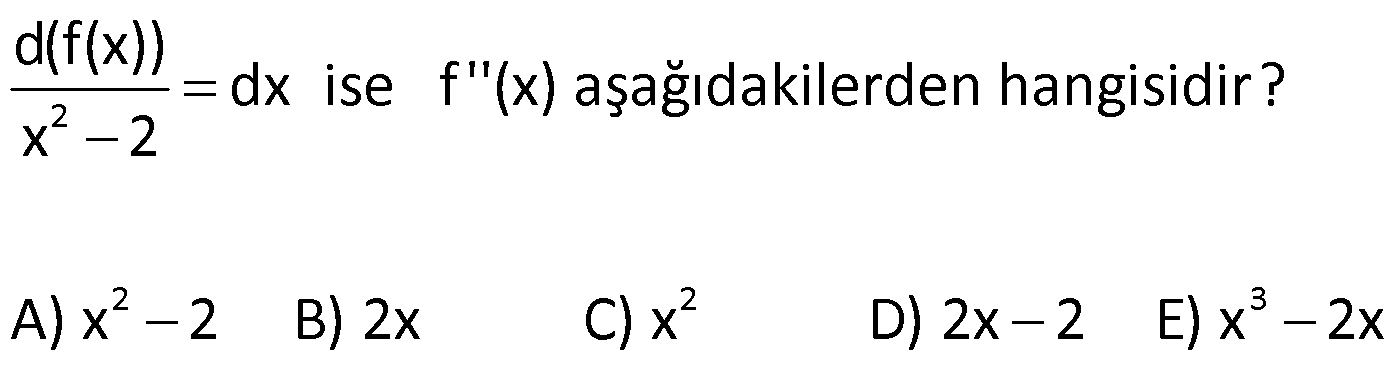
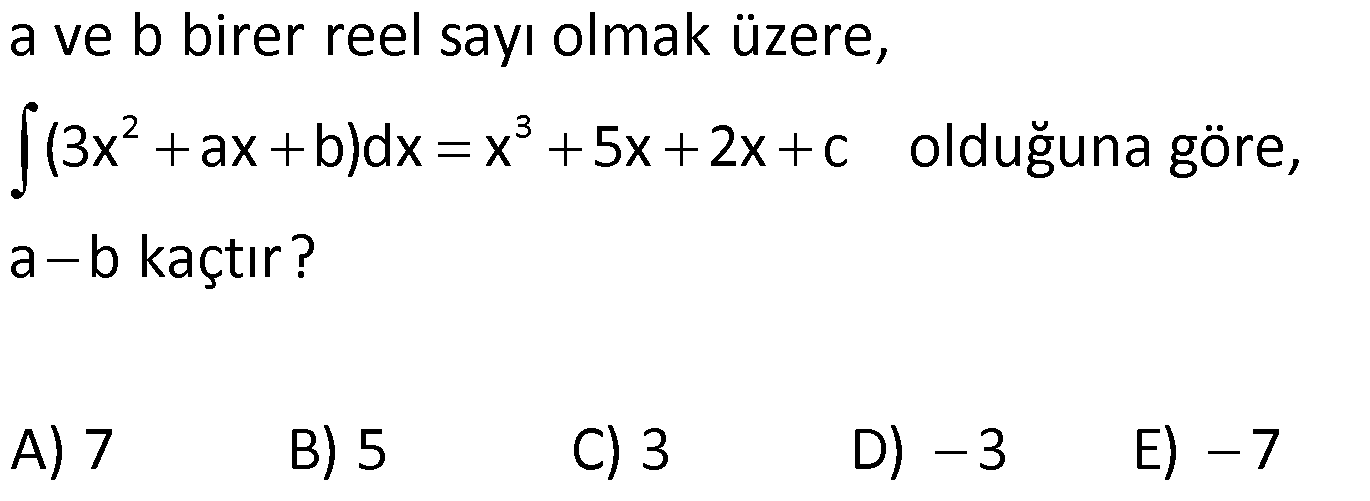
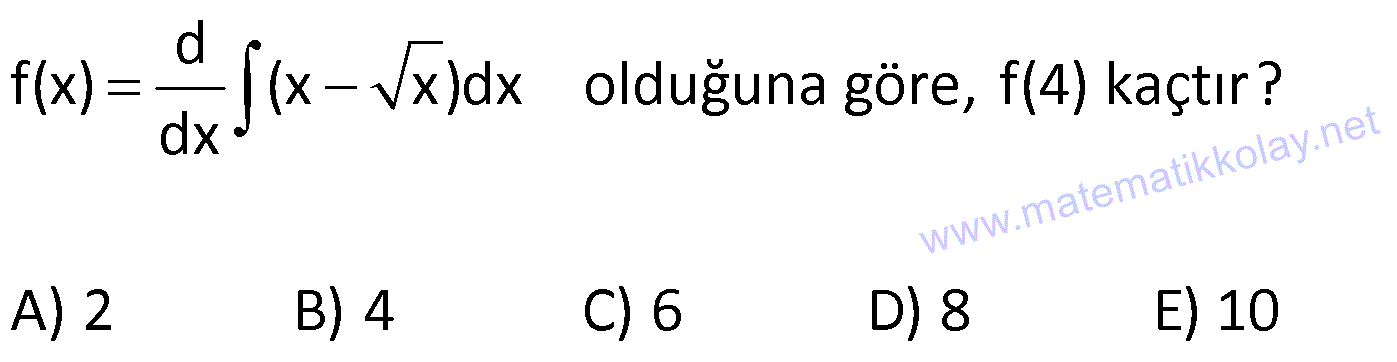
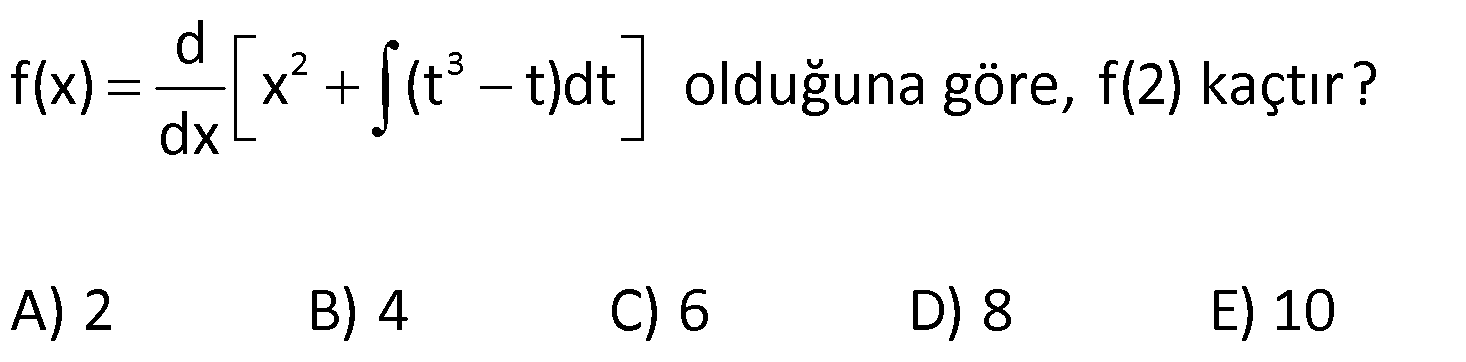
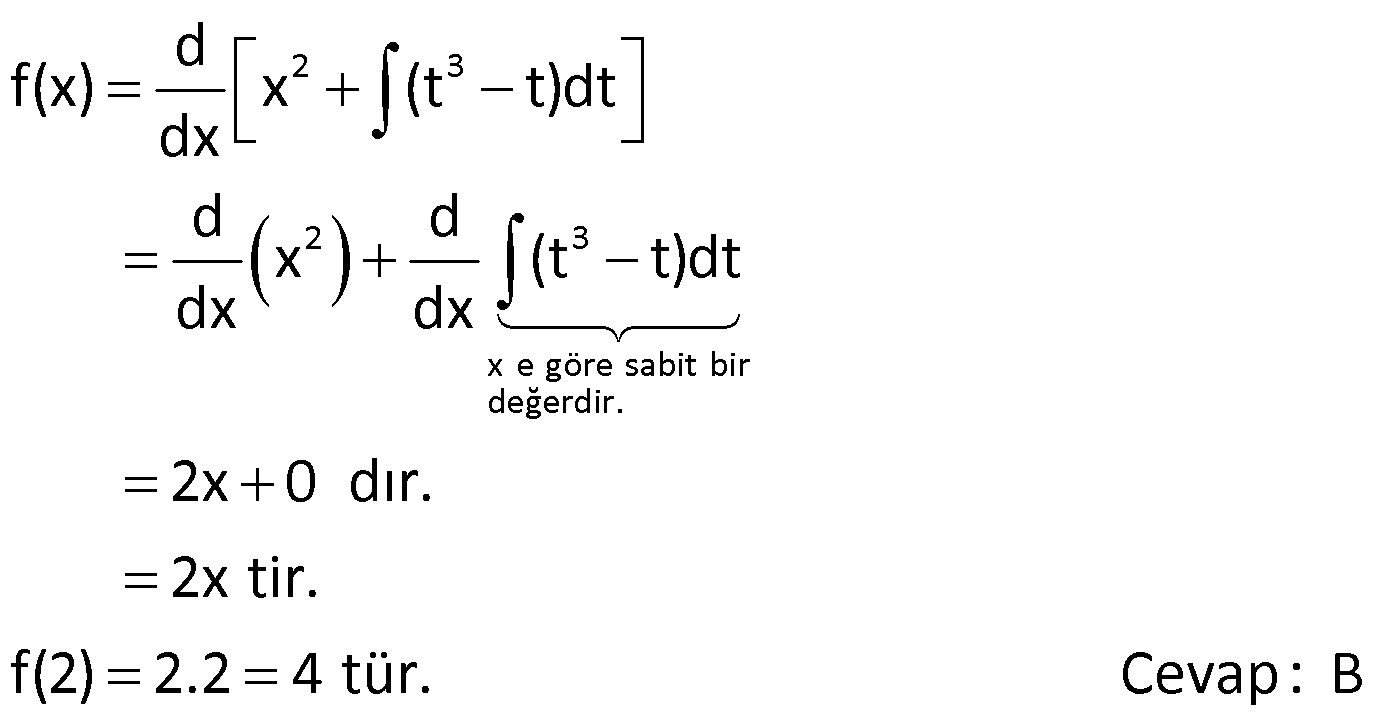
hocam sınava 4 ay kaldı lütfen artık ekleyin şu soruları
Soruları yeniden oluşturuyoruz. Kısmetse 1 ay içinde integrale geçeceğiz.
Hocam Nisan ayının yarısına geldik lütfen ekleyin artık
sorular oluşturulmaktadır. ilginiz için teşekkür ederiz.
Sorular yüklenme aşamasındadır, biraz daha sabretmenizi rica edeceğiz. Anlayışınız için teşekkürler.
Admin olmayan AdminBey, benim yerime cevap vermiş :))
İşin doğrusu şu,
Maalesef, dolaylı yollardan da olsa, koronadan işler aksıyor.
Ben korona olmasam da, olan biri nedeniyle iş yoğunluğum başka yöne kayıyor.
Bu sebeple gecikmeler yaşanıyor.
Bu aralar, integralin ilk kısmı ile ilgili sorular hazırlanıyor. Yakında ilk yüklemesi yapılacak.