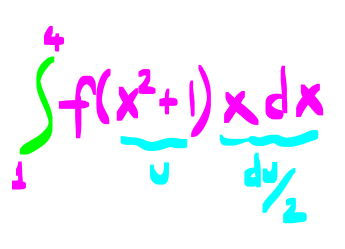Bu bölümde Belirli İntegralde Değişken Değiştirme ile ilgili 12 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
Çözüm için Tıklayınız.
2.SORU
| | | | | |
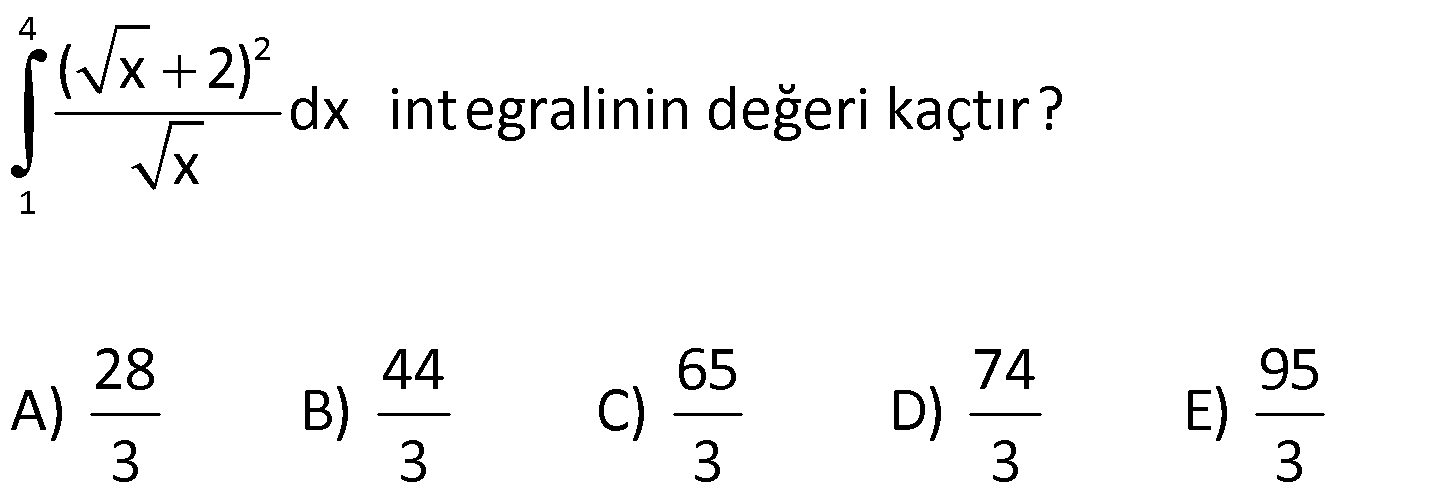
Çözüm için Tıklayınız.
3.SORU
| | | | | |
Çözüm için Tıklayınız.
4.SORU
| | | | | |
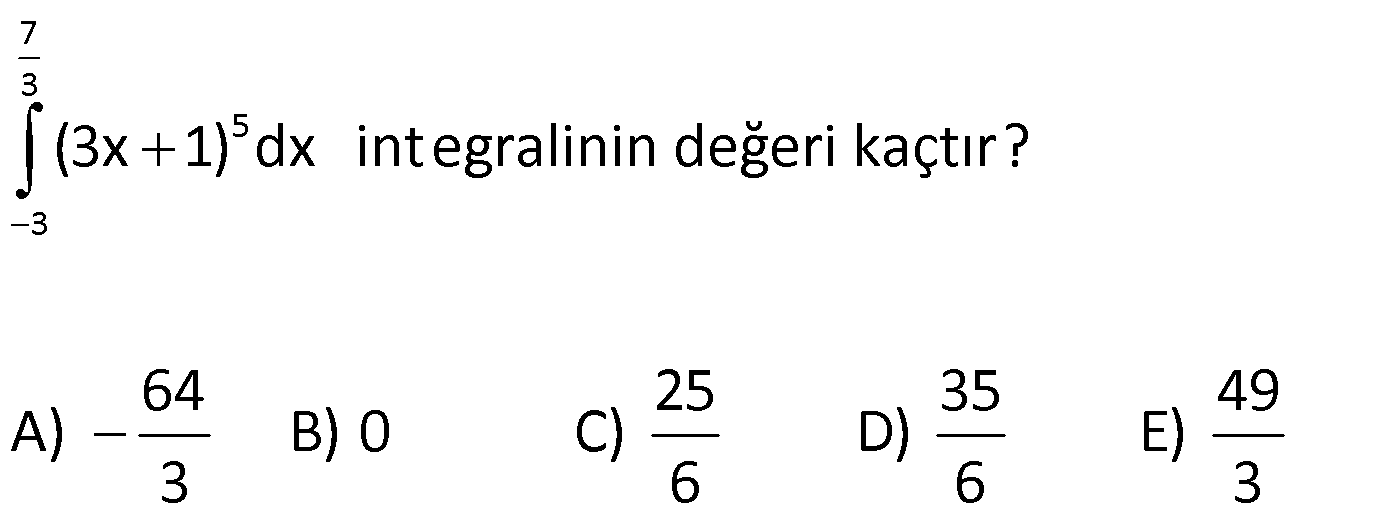
Çözüm için Tıklayınız.
5.SORU
| | | | | |
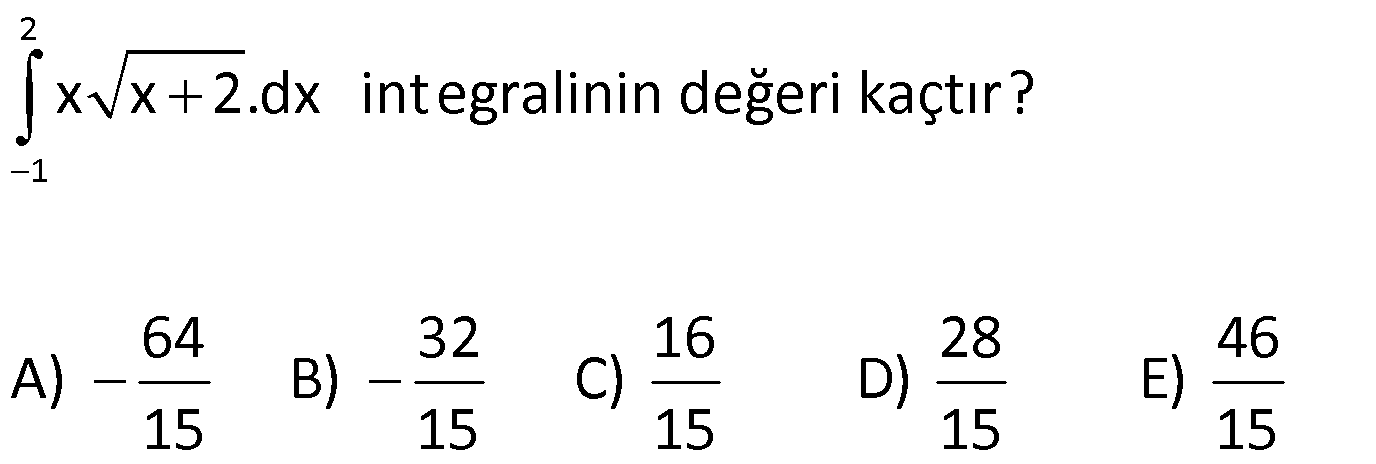
Çözüm için Tıklayınız.
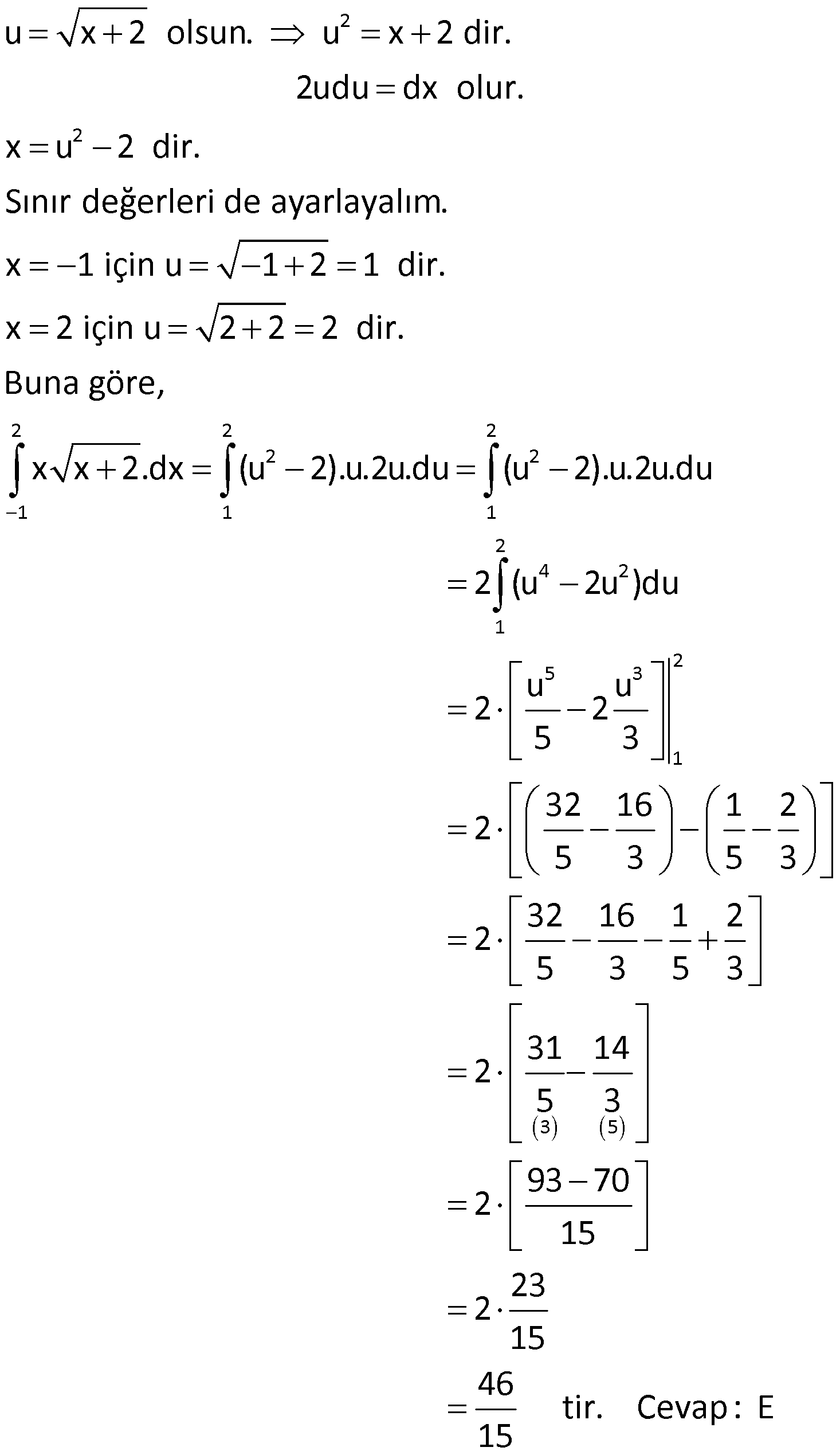
6.SORU
| | | | | |
Çözüm için Tıklayınız.
7.SORU
| | | | | |
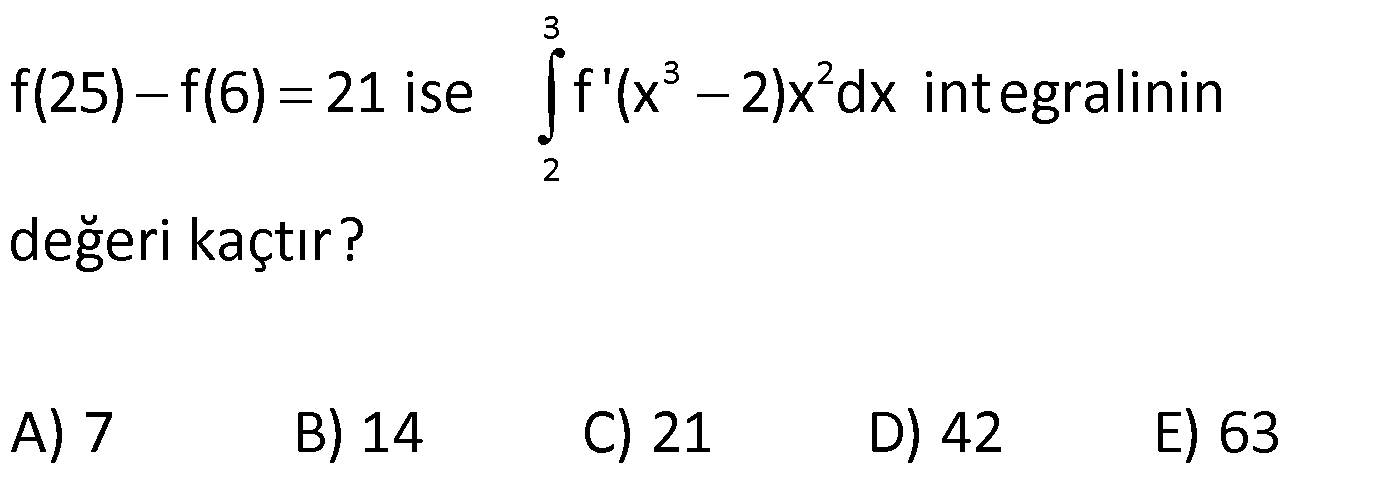
Çözüm için Tıklayınız.
8.SORU
| | | | | |
Çözüm için Tıklayınız.
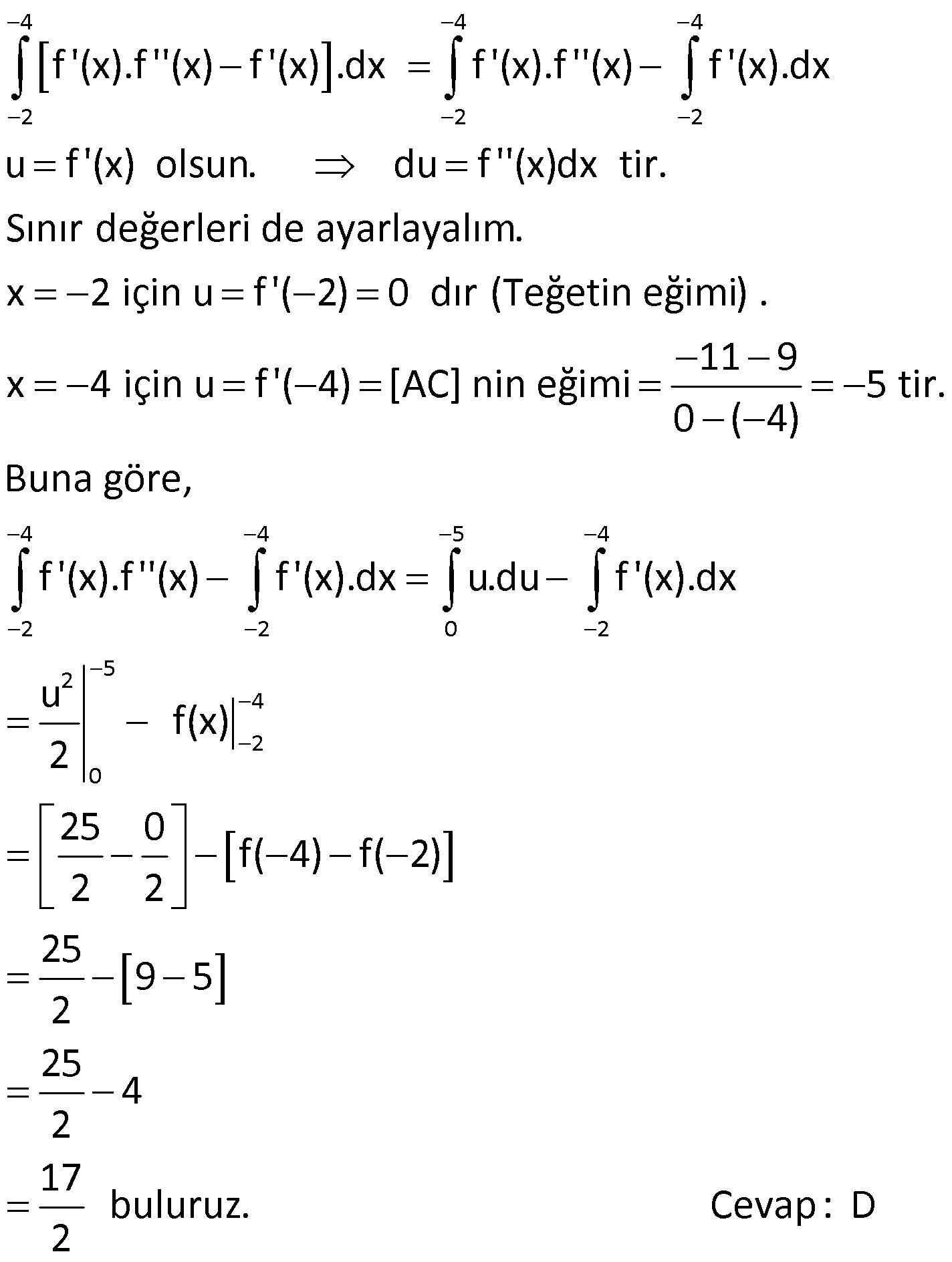
9.SORU
| | | | | |
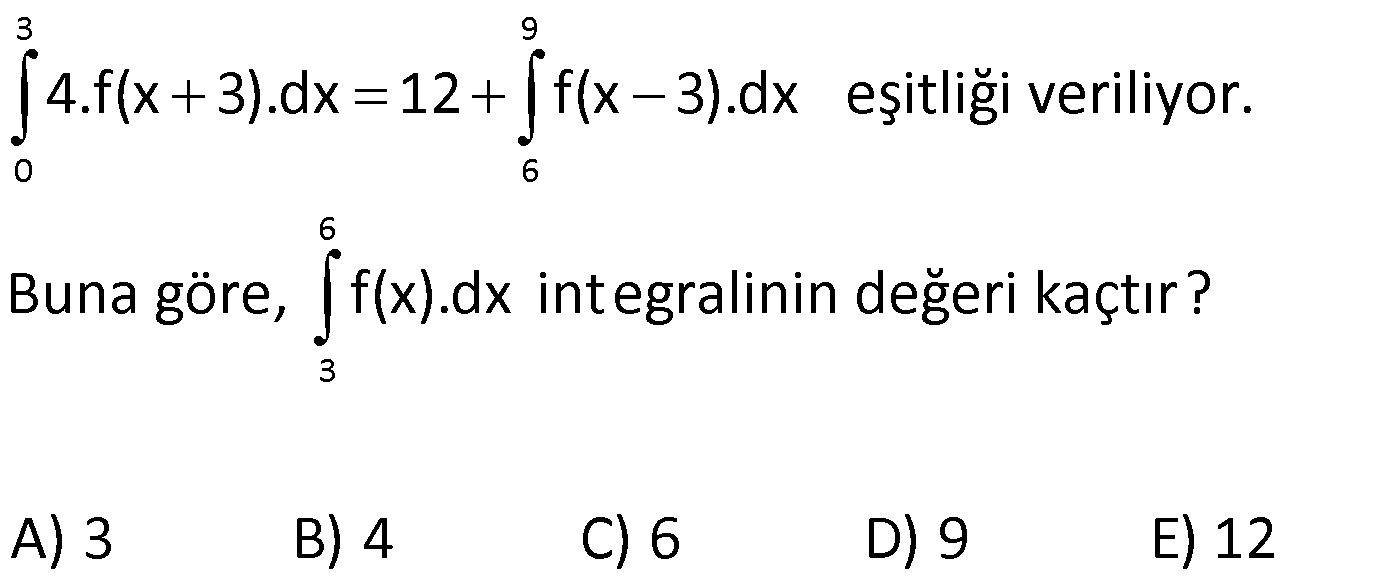
Çözüm için Tıklayınız.
10.SORU
| | | | | |
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
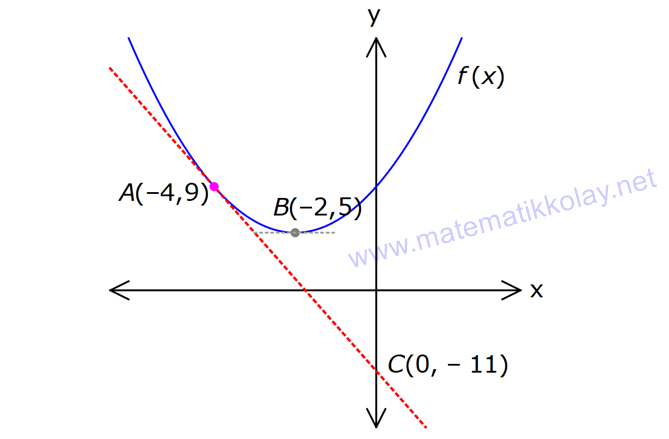
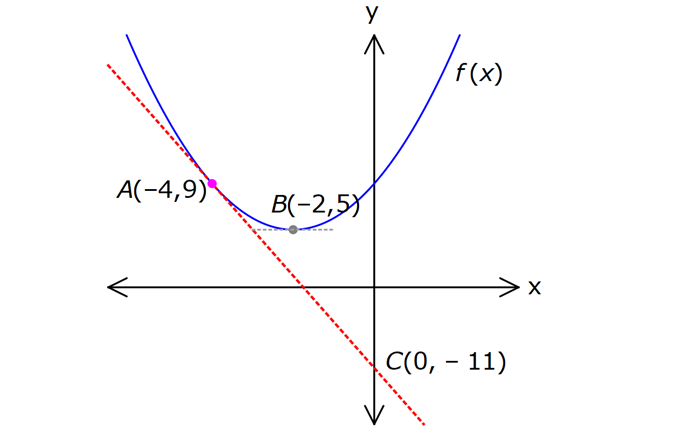
BELİRLİ İNTEGRALDE DEĞİŞKEN DEĞİŞTİRME www.matematikkolay.net 1) 0 3 5 2 1 3(x 2) x dx integralinin değeri kaçtır? 1 21 55 128 243 A) B) C) D) E) 6 2 6 3 4 ÇÖZÜM: 3 2 3 Belirli integralde değişken değiştirdikten sonra sınır değerleri de yeniden düzenlemeliyiz. x 2 u dersek, 3x dx du olur. Sınır değerleri de ayarlayalım. x 1 için u ( 1) 2 1 dir. x 0 içi Not : 3 0 2 3 5 2 5 1 1 2 6 1 n u (0) 2 2 dir. Buna göre, 3(x 2) x dx u du u 6 64 1 6 6 63 21 buluruz. Cevap: B 6 2 2) 4 2 1 ( x 2) dx integralinin değeri kaçtır? x 28 44 65 74 95 A) B) C) D) E) 3 3 3 3 3 ÇÖZÜM: 4 4 2 2 2 1 3 1 x 2 u dersek, dx du olur. 2 x dx 2du dur. x Sınır değerleri de ayarlayalım. x 1 için u 1 2 3 tür. x 4 için u 4 2 4 tür. Buna göre, ( x 2) dx u .2du 2 u .du x 4 3 4 3 3 u 2 3 64 27 2 3 3 37 2 3 74 buluruz. Cevap: D 3 3) 1 2 3 1 (x 2x) (4x 4)dx integralinin değeri kaçtır? 21 55 128 243 A) 40 B) C) D) E) 2 6 3 4 ÇÖZÜM: www.matematikkolay.net 2 2 2 1 3 3 2 3 3 3 1 1 1 x 2x u dersek, (2x 2)dx du olur. Sınır değerleri de ayarlayalım. x 1 için u ( 1) 2 1 2 1 dir. x 1 için u (1) 2 3 tür. Buna göre, (x 2x) (4x 4)dx u .2du 2 u .du 3 4 1 u 2 4 81 1 2 4 4 2 20 40 t ır. Cevap : A 4) 7 3 5 3 (3x 1) dx integralinin değeri kaçtır? 64 25 35 49 A) B) 0 C) D) E) 3 6 6 3 ÇÖZÜM: 7 3 8 8 5 5 5 3 8 8 Tek fonks. 3x 1 u dersek, 3dx du olur. Sınır değerleri de ayarlayalım. x 3 için u 3( 3) 1 8 dir. 7 7 x için u 3 1 8 dir. 3 3 Buna göre, du 1 (3x 1) dx u u .du 0 dır. Cevap: B 3 3 5) 2 1 x x 2.dx integralinin değeri kaçtır? 64 32 16 28 46 A) B) C) D) E) 15 15 15 15 15 ÇÖZÜM: 2 2 2 2 1 u x 2 olsun. u x 2 dir. 2udu dx olur. x u 2 dir. Sınır değerleri de ayarlayalım. x 1 için u 1 2 1 dir. x 2 için u 2 2 2 dir. Buna göre, x x 2.dx (u 2).u.2u. 2 2 2 1 1 2 4 2 1 2 5 3 1 du (u 2).u.2u.du 2 (u 2u )du u u 2 2 5 3 3 5 32 16 1 2 2 5 3 5 3 32 16 1 2 2 5 3 5 3 31 14 2 5 3 93 70 2 15 23 2 15 46 ti 15 r. Cevap : E www.matematikkolay.net 6) 4 1 3 1 f(4x 1)dx 12 olduğuna göre, f(3x 6)dx integralinin değeri kaçtır? A) 8 B) 12 C) 16 D) 24 E) 36 ÇÖZÜM: 4 1 4 15 1 3 15 3 f(4x 1)dx 12 verilmiş. u 4x 1 olsun. du 4dx tir. Sınır değerleri de ayarlayalım. x 1 için u 4 1 3 tür. x 4 için u 16 1 15 tir. Buna göre, du f(4x 1)dx 12 f(u) 12 4 1 f(u)du 4 15 3 3 1 12 f(u)du 48 dir. Şimdi, f(3x 6)dx integraline bakalım. u 3x 6 olsun. du 3dx tir. Sınır değerleri de ayarlayalım. x 1 için u 3 6 3 tür. x 3 için u 9 6 15 tir. Buna göre, f(3x 3 15 15 1 3 3 48 du 1 48 6)dx f(u) f(u)du 16 dır. 3 3 3 Cevap : C 7) 3 3 2 2 f(25) f(6) 21 ise f'(x 2)x dx integralinin değeri kaçtır? A) 7 B) 14 C) 21 D) 42 E) 63 ÇÖZÜM: 3 3 2 2 3 2 3 25 25 3 2 2 6 6 f'(x 2)x dx u x 2 olsun. du 3x dx tir. Sınır değerleri de ayarlayalım. x 2 için u 8 2 6 dır. x 3 için u 27 2 25 tir. Buna göre, du 1 f'(x 2)x dx f'(u) f'(u)du 3 3 25 6 21 1 f(u) 3 1 f(25) f(6) 3 7 buluruz. Cevap: A 8) 4 2 Yukarıda f(x) fonksiyonunun grafiği verilmiştir. Buna göre, f'(x).f”(x) f'(x) .dx integralinin sonucu kaçtır? 9 13 15 17 19 A) B) C) D) E) 2 2 2 2 2 ÇÖZÜM: www.matematikkolay.net 4 4 4 2 2 2 f'(x).f”(x) f'(x) .dx f'(x).f”(x) f'(x).dx u f'(x) olsun. du f”(x)dx tir. Sınır değerleri de ayarlayalım. x 2 için u f'( 2) 0 dır (Teğetin eğimi) . x 4 için u f'( 4) [AC] n 4 4 5 4 2 2 0 2 5 2 4 2 0 11 9 in eğimi 5 tir. 0 ( 4) Buna göre, f'(x).f”(x) f'(x).dx u.du f'(x).dx u f(x) 2 25 0 f( 4) f( 2) 2 2 25 9 5 2 25 4 2 17 buluruz. 2 Cevap: D 9) 3 9 0 6 6 3 4.f(x 3).dx 12 f(x 3).dx eşitliği veriliyor. Buna göre, f(x).dx integralinin değeri kaçtır? A) 3 B) 4 C) 6 D) 9 E) 12 ÇÖZÜM: b k b k a k a k u x k du dx u a k k a alt u b k k b üst b f(u)du a Değişken değiştirerek de görebileceğimiz bu durumu kısaca şu şekilde ifade edebiliriz: f(x k)dx f(x k)dx Not : Belirli İntegralde Öteleme b a u x k du dx u a k k a alt u b k k b üst b f(u)du a 3 9 6 63 f(x)dx tir. Buna göre, f(x 3)dx f(x 3)dx f(x)dx A diyebiliriz. Sorudaki eşitlik, 4A 12 A haline gelir. 3A 12 A 4 buluruz. Cevap: B 10) 5 2 16 12 f(x) fonksiyonu bir tek fonksiyondur. f(x 2).dx 8 olduğuna göre, x f dx integralinin değeri kaçtır? 4 A) 32 B) 16 C) 8 D) 2 E) 2 ÇÖZÜM: www.matematikkolay.net 5 3 2 4 u x 2 du dx u 4 u 3 alt üst 4 4 3 4 4 4 3 3 8 f(x 2).dx 8 f(x).dx 8 dir. Tek fonksiyon olduğuna göre, f(x).dx 0 olmalıdır. f(x).dx f(x).dx 0 f(x).dx 8 dir. Sorulan inegrale ba 16 4 4 12 3 3 x dx 8 u du 4 4 u 3 u alt üst 4 kalım. x f dx f u 4du 4 f u du 32 dir. 4 Cevap : A
