11.SORU

| | | | | |
Çözüm için Tıklayınız.

12.SORU
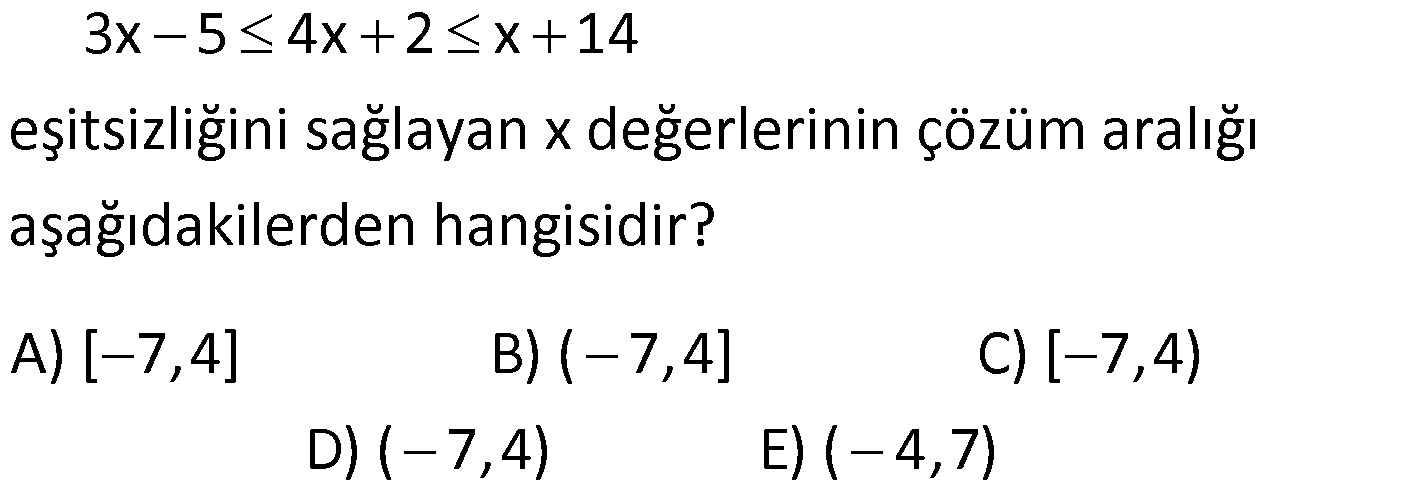
 | | | | |
Çözüm için Tıklayınız.

13.SORU

| | | | | |
Çözüm için Tıklayınız.
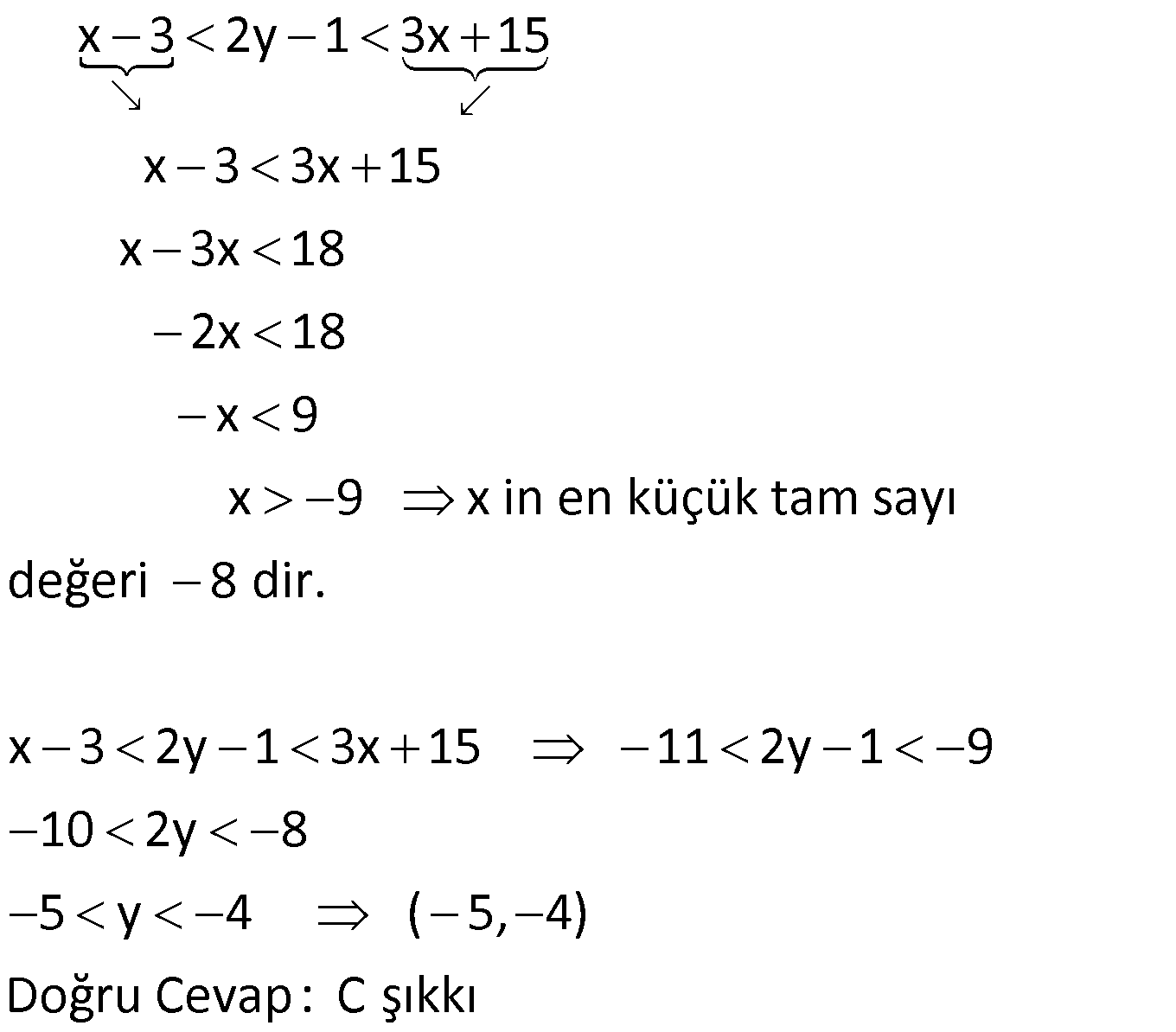
14.SORU

| | | | | |
Çözüm için Tıklayınız.

15.SORU

| | | | | |
Çözüm için Tıklayınız.

16.SORU
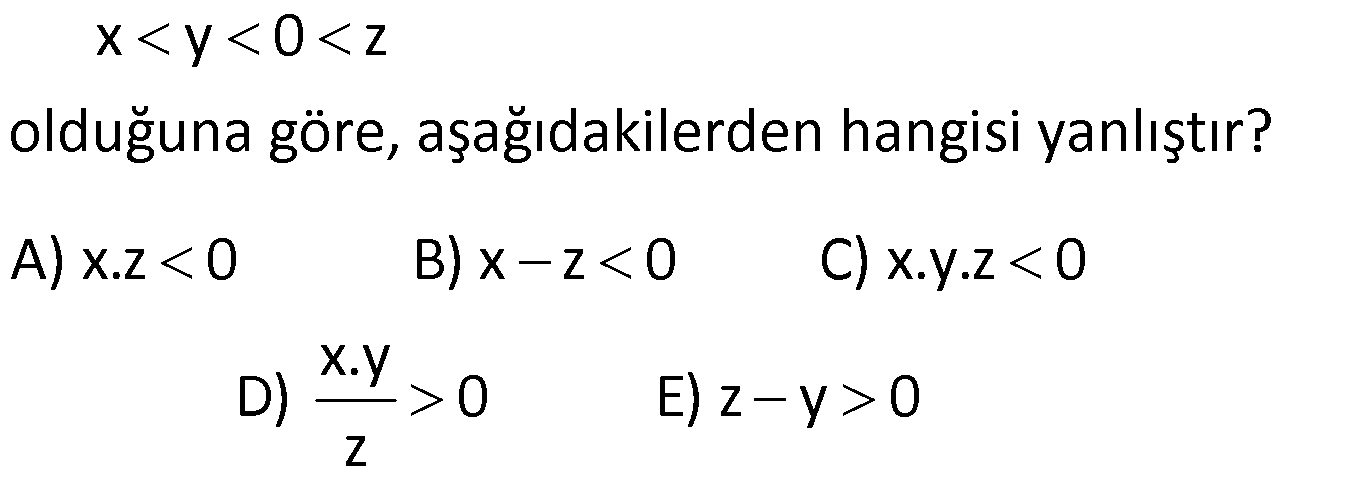
| | | | | |
Çözüm için Tıklayınız.
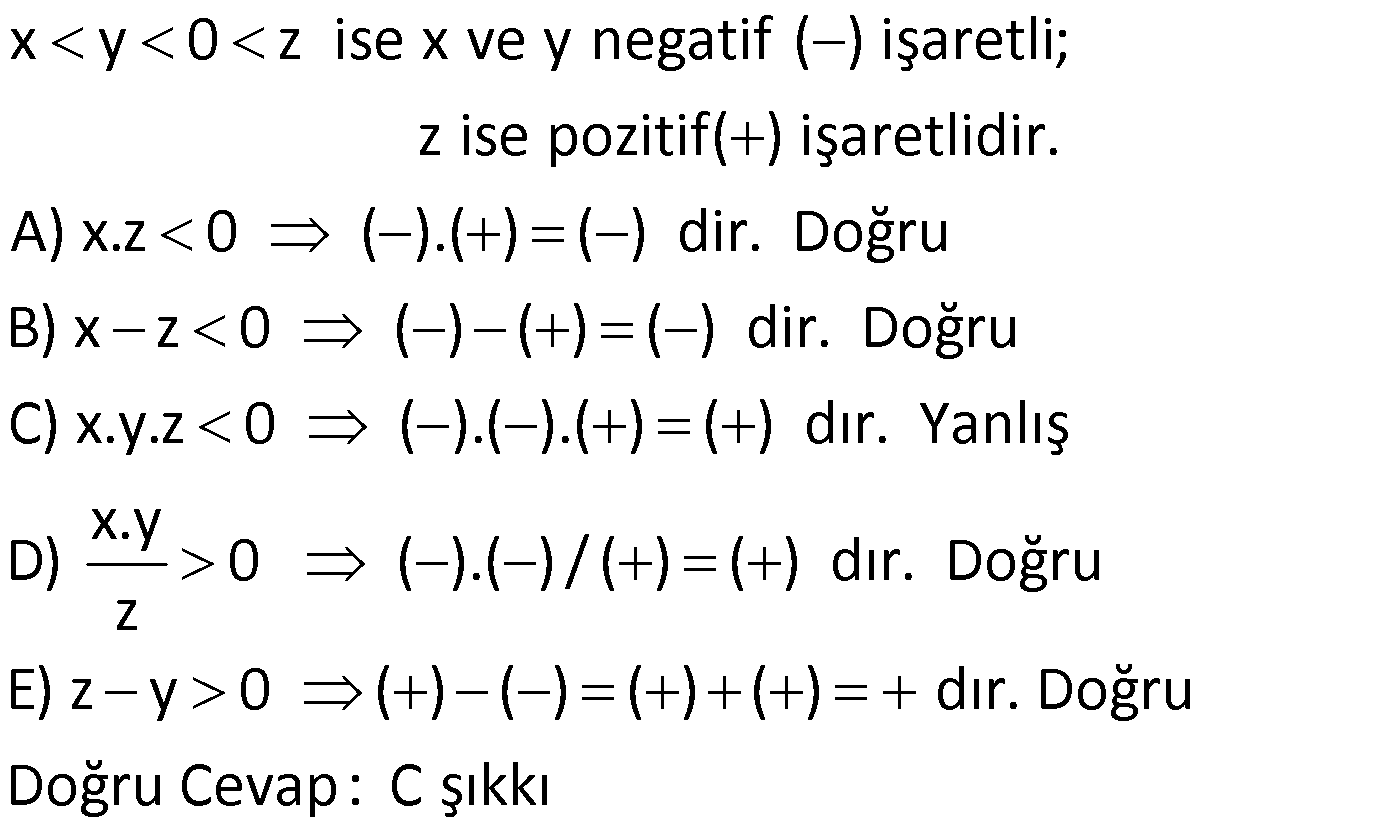
17.SORU
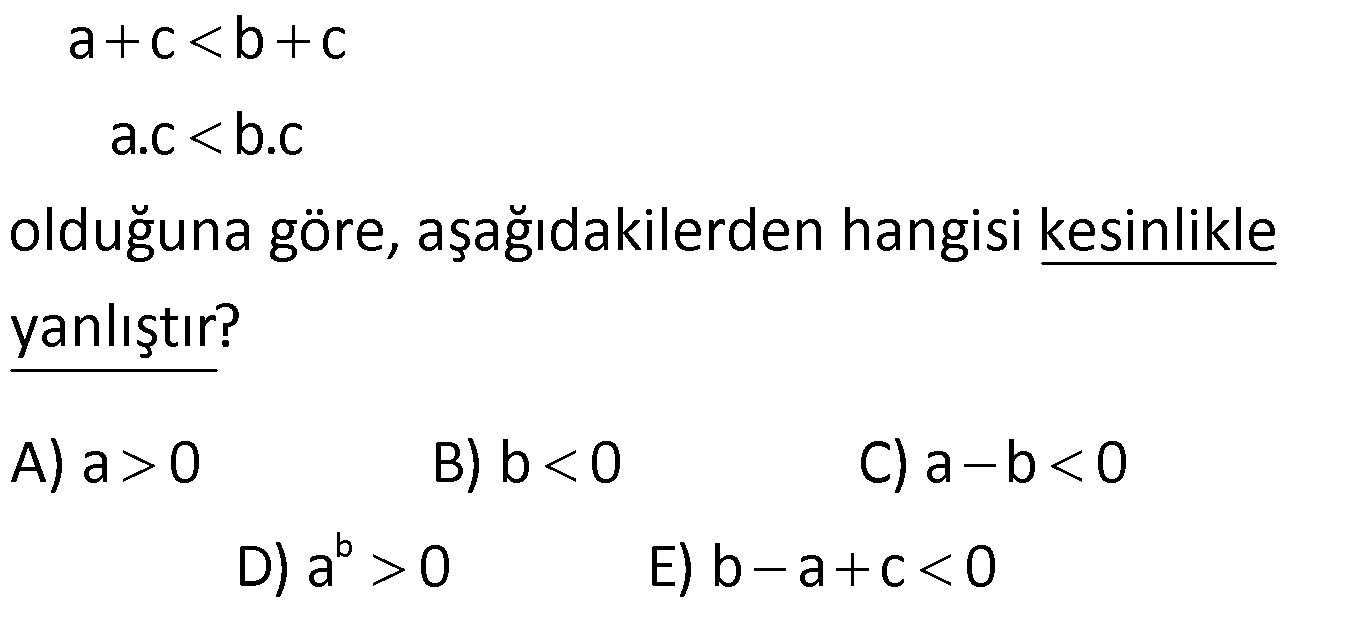
| | | | | |
Çözüm için Tıklayınız.

18.SORU

 | | | | |
Çözüm için Tıklayınız.

19.SORU

| | | | | |
Çözüm için Tıklayınız.

20.SORU

| | | | | |
Çözüm için Tıklayınız.

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
10) 7 2x 1 5 x olduğuna göre 2 ifadesinin alabileceği tam 3 sayı değerlerinin toplamı kaçtır? A) 3 B) 4 C) 5 D) 6 E) 7 ÇÖZÜM: İlk önce x ‘in değer aralığını bulalım. 7 2x 1 5 (Her tarafa 1 ekleyelim) 6 2x 6 (Her tarafı 2 ye bölelim) 3 x 3 buluruz. x Şimdi 2 nin değer aralığını bulalı 3 m. 3 x 3 (Her tarafı 3 e bölelim) x 1 1 (Her tarafa 2 ekleyelim) 3 x 1 2 3 Bu ifade 2 ve 3 değerlerini 3 alabilir. Toplam: 2 3 5 buluruz. Doğru Cevap : C şıkkı ? ? 11) 7 2x 1 17 ve 3x 2y 1 0 olduğuna göre, y nin alabileceği kaç farklı x tamsayı değeri var dır? A) 14 B) 15 C) 16 D) 17 E) 18 ? www.matematikkolay.net ÇÖZÜM: İlk önce x ‘in değer aralığını bulalım. 7 2x 1 17 (Her tarafa 1 ekleyelim) 6 2x 18 (Her tarafa 2 ye bölelim) 3 x 9 3x 2y 1 0 eşitliğinde x ‘i y cinsinden yazalım. 3x 2y 1 2y 1 x Bu 3 ? ? ? nu x’in değer aralığına yazalım. 2y 1 3 x 9 3 9 3 9 2y 1 27 8 2y 28 4 y 14 4 y 14 Buna göre; y 14 ten 3 e kadar tüm tam sayı değerlerini alabilir. Son Terim İlk Terim Terim Sayısı Artış? ? ? 1 Miktarı 3 ( 14) 1 18 buluruz. 1 Doğru Cevap : E şıkkı ? ? 12) 3x 5 4x 2 x 14 eşitsizliğini sağlayan x değerlerinin çözüm aralığı aşağıdakilerden hangisidir? A) [ 7,4] B) ( 7,4] C) [ 7,4) D) ( 7,4) E) ( 4,7) ÇÖZÜM: Buraya bakalım 3x 5 4x 2 x 14 eşitsizliğindeki x değerlerini bulmak için 2 parça halinde inceleyelim. 1.durum: 3x 5 4x 2 x 14 3x 5 4x 2 x 2 5 x 7 x 7 ?Buraya bakalım 2.durum: 3x 5 4x 2 x 14 4x 2 x 14 3x 12 x 4 Bu iki duruma göre Ç.K: [ 7,4] tür. Doğru Cevap : A şıkkı 13) x 3 2y 1 3x 15 eşitsizliğini sağlayan en küçük x tam sayı değeri için y nin değer aralığı aşağıdakilerden hangisidir? A) [ 7,4) B) [ 7,4] C) ( 5, 4) D) [ 5, 4) E) ( 5, 4] ÇÖZÜM: x 3 2y 1 3x 15 x 3 3x 15 x 3x 18 2x 18 x 9 x 9 x in en küçük tam sayı değeri 8 dir. x 3 2y 1 3x 15 11 2y 1 9 ? ? 10 2y 8 5 y 4 ( 5, 4) Doğru Cevap : C şıkkı ? 14) 1 1 1 12 x 3 6 olduğuna göre, x in alabileceği en küçük ve en büyük tam sayı değerlerinin toplamı kaçtır? A) 10 B) 12 C) 13 D) 14 E) 15 www.matematikkolay.net ÇÖZÜM: 1 1 1 eşitsizlikteki kesirleri ters çevirirsek 12 x 3 6 eşitsizlik yön değiştirir. 12 x 3 6 12 x 3 6 1 1 1 12 3 x 6 3 9 x 3 Buna göre x’in en büyük tam sayı değeri 8 , en küçük tam sayı değeri 4 t ? ? ür. Bunların toplamı da 8 4 12 bulunur. Doğru Cevap : B şıkkı ? 15) 0 y x olmak üzere, y.z 3x 5y eşitliğini sağlayan z değerleri için aşağıdakilerden hangisi doğrudur? A) z 3 B) 3 z 5 C) 3 z 8 D) z 8 E) z 8 ? ÇÖZÜM: y.z 3x 5y eşitliğinde her tarafı y ‘ ye bölersek; 3x z 5 olur. y 0 y x eşitsizliğinde her tarafı y e bölelim. 0 y x x 0 1 ( 3 ile çarpalım) y y y y 3x 0 3 (Her tarafa 5 ekleyelim) y 3x 5 8 5 y ?? ? ? ? 8 z z 8 dır. Doğru Cevap : E şıkkı ?16) x y 0 z olduğuna göre, aşağıdakilerden hangisi yanlıştır? A) x.z 0 B) x z 0 C) x.y.z 0 x.y D) 0 E) z y 0 zÇÖZÜM: x y 0 z ise x ve y negatif ( ) işaretli; z ise pozitif( ) işaretlidir. A) x.z 0 ( ).( ) ( ) dir. Doğru B) x z 0 ( ) ( ) ( ) dir. Doğru C) x.y.z 0 ? ? ? ? ( ).( ).( ) ( ) dır. Yanlış x.y D) 0 ( ).( ) / ( ) ( ) dır. Doğru z E) z y 0 ( ) ( ) ( ) ( ) dır. Doğru Doğru Cevap : C şıkkı ? ? ? ? ? ? ?17) b a c b c a.c b.c olduğuna göre, aşağıdakilerden hangisi kesinlikle yanlıştır? A) a 0 B) b 0 C) a b 0 D) a 0 E) b a c 0 ÇÖZÜM: a c b c a b dir. a.c b.c a b eşitsizliğinin her iki tarafı c ile çarpılmış ve eşitsizlik yön değiştirmemiş. Buna göre; c 0 dır. A) a 0 kesinlikle yanlış olduğunu bilemeyiz. B) b 0 kesinl ? ? ? ? b ikle yanlış olduğunu bilemeyiz. C) a b 0 a, b den küçüktü. Kesinlikle doğru D) a 0 kesinlikle yanlış olduğunu bilemeyiz. E) b a c 0 (b a) pozitiftir, c de pozitif idi. Bu ikisinin toplamı 0 dan b? ? ?üyüktür. Kesinlikle yanlış olan şık budur. Doğru Cevap: E şıkkı www.matematikkolay.net 18) 2 a.b.c 0 a.b 0 a.c 0 olduğuna göre, a,b ve c nin işaretleri sırasıyla aşağıdakilerden hangisi olabilir? A) , , B) , , C) , , D) , , E) , , ÇÖZÜM: 2 2 a.b 0 b pozitiftir; buna göre a pozitiftir. a.c 0 a ile c zıt işaretlidir. a pozitif ise; c negatiftir. a.b.c 0 a pozit ? ? ? ? if ve c negatifti. Çarpımın negatif olması için b pozitif olmalıdır. Buna göre işaretler : , , dir. Doğru Cevap : A şıkkı 19) 2 a a olmak üzere, 4a 3 ifadesinin alabileceği tam sayı değerlerinin toplamı kaçtır? A) 9 B) 13 C) 14 D) 15 E) 16 ÇÖZÜM: 2 Sadece 0 ile 1 arasındaki sayıların karesi kendisinden küçüktür. a a 0 a 1 dir. 0 a 1 (Her tarafı 4 ile çarpalım) 0 4a 4 (Her tarafa 3 ekleyelim) 3 4a 3 7 Buna göre 4a 3 : 4,5,6 değe ? rlerini alabilir. Toplam: 4 5 6 15 bulunur. Doğru Cevap : D şıkkı?



Allah sizden razı olsun . çok iyi bir site. Geliştirmeniz dileğiyle ??
canımsın teşekkür ederiz yarumların için.
Yılları neden yok
Burdaki sorular, çıkmış sorular değil.
4.sorunun 3 tane doğru cevabı var. A, C , E
Uyarınız için teşekkürler. Aynı şık 3 defa yazılmış. Şimdi hata düzeltildi. Tek bir şık doğru, artık.
Karşılaştığım bir soru türünün çözümünü öğrenmek için tesadüfen siteyi buldum, gerçekten çok yararlı bir site, Artık bu siteden bakacağım soru ve çözümlere, ayrıca emeği geçen herkese teşekkür ederim .
6.soruda +6 nasıl -6’ya dönüştü?
– işareti 3x+6 nın üzerine dağıtıldı. -3x ve -6 oldu.
iyi akşamlar soru 21 de cevap nasıl 14 oluyor takip ettiğim bi kanalda matematik hocası iki tane < var iste büyük değer ile küçük değeri çıkarıp farktan 1 çıkarın bir küçük eşit veya vea büyük eşit ile < varsa sonuç büyükle küçük sayının farkı iki işarette küçük eşit ile büyük eşit iste farka +1 ekleyin demişti yanlış mı anlattı acaba yoksa sizin cevap mı hatalı ?
Dediğiniz şey hatalı değil. Sorunun çözümü de hatalı değil.
Dediğiniz şeyi uygularsanız, zaten 21-7=14 ü bulursunuz.
Ama, biz burada hep terim sayısını formülünü kullanıyoruz.
Terim Sayısı=(Son Terim-İlk Terim)/Artış Miktarı + 1
Bu soruda da istenen ifade 8,9,10,…,21 e kadar değerler alabiliyor.
Terim Sayısı=(21-8)/1 + 1 = 13+1=14 buluyoruz.
11.soruda cevap 18 demiş çünkü 18 sayı var ama soruda tam sayıları istiyor yani sıfırı sayamayız o yüzden cevabın 17 olması gerekiyor.
0 sayısı da bir tam sayıdır.
👍👍