2.Dereceden Denklemler

2.Sayfa için Tıklayınız.

21.SORU

Çözüm için Tıklayınız.

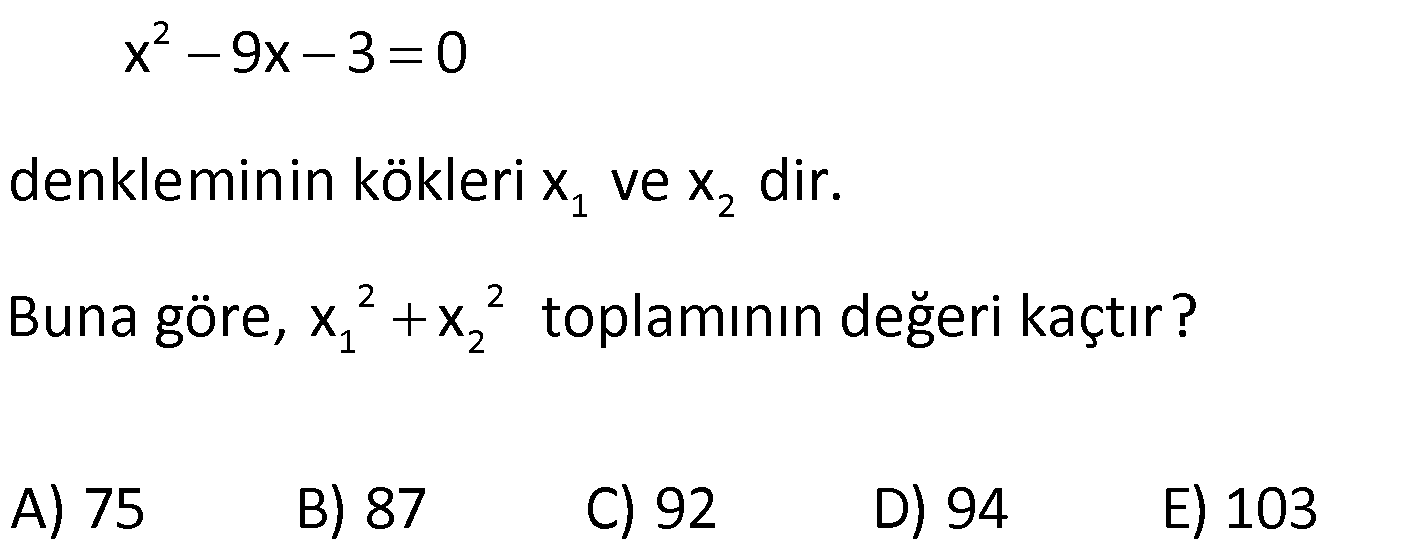
22.SORU


Çözüm için Tıklayınız.

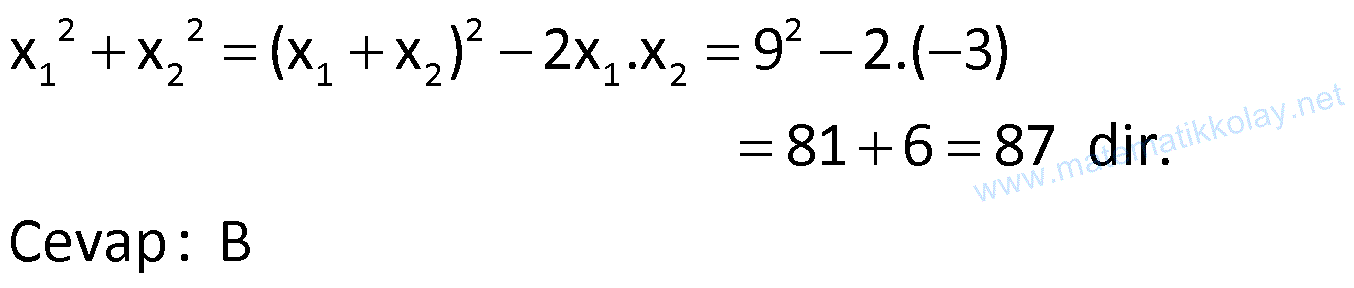
23.SORU

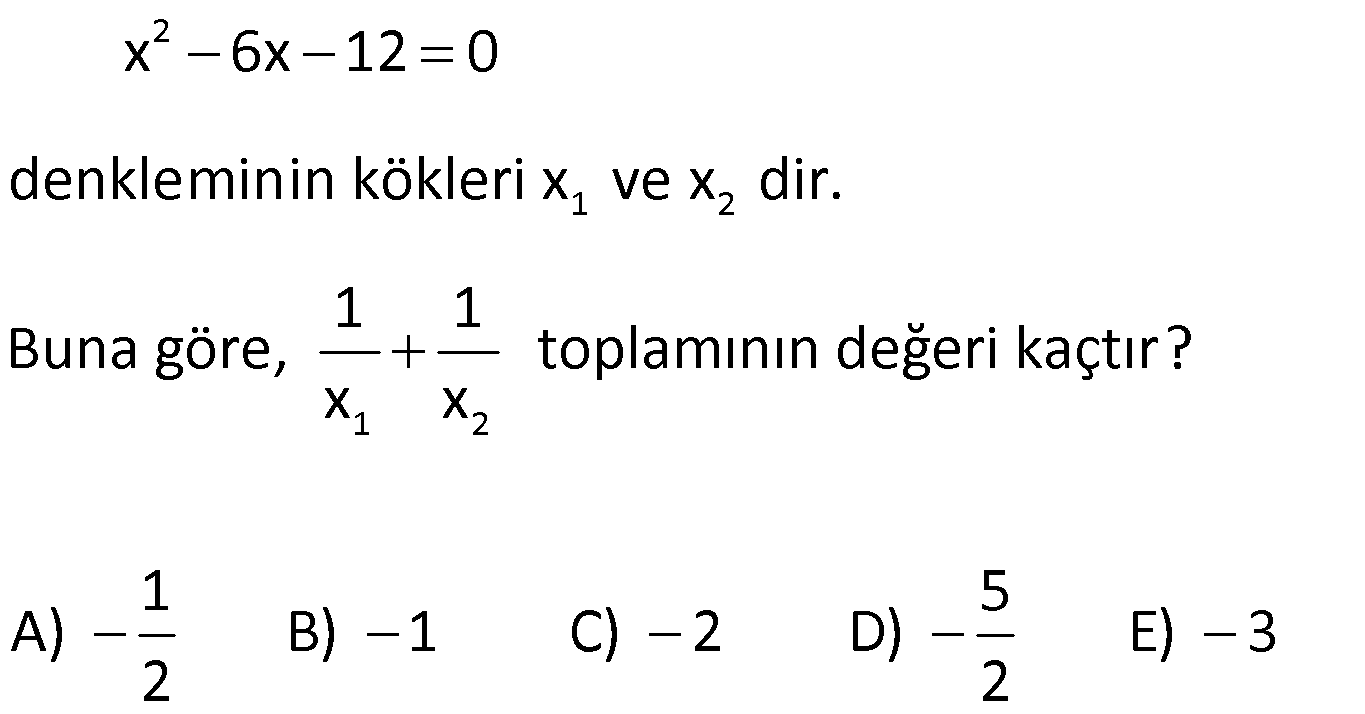
Çözüm için Tıklayınız.

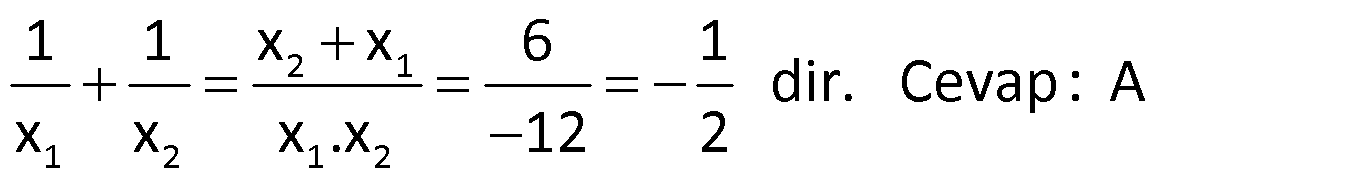
24.SORU

Çözüm için Tıklayınız.

25.SORU

Çözüm için Tıklayınız.

26.SORU

Çözüm için Tıklayınız.

27.SORU

Çözüm için Tıklayınız.

28.SORU

Çözüm için Tıklayınız.

29.SORU

Çözüm için Tıklayınız.

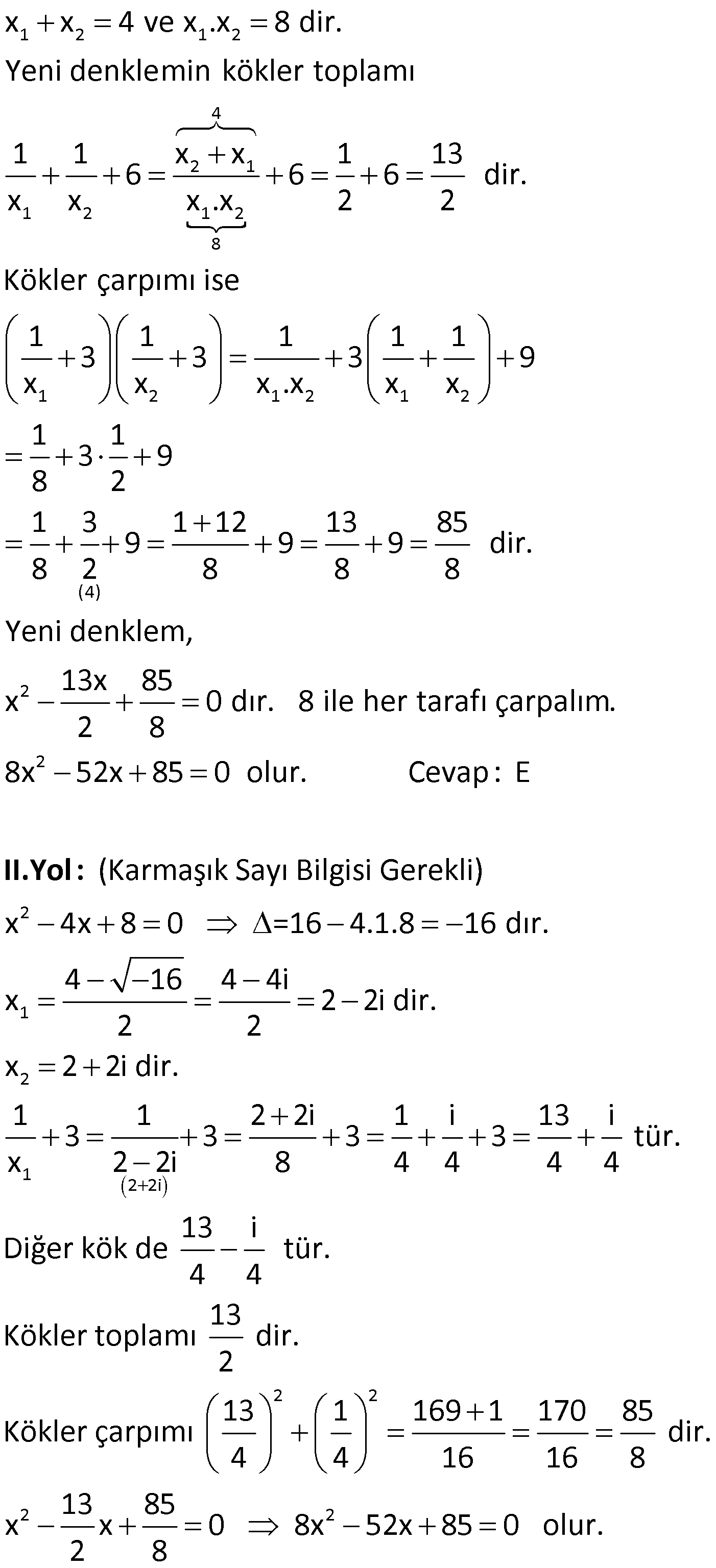
30.SORU

Çözüm için Tıklayınız.

Sorular Bitti. Konu Anlatımı veya Daha Fazla Soru için Tıklayabilirsiniz.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
21) 2 1 2 2 1 2 1 x kx 12 0 denkleminin kökleri x ve x dir. x .x 36 olduğuna göre, k x kaçtır? A) 5 B) 1 C) 3 D) 4 E) 5 ÇÖZÜM: 1 2 2 1 2 1 2 2 2 12 2 1 2 1 3 1 c 12 x .x 12 dir. a 1 x .x 36 ise x .x .x 36 x 3 tür. Bu değeri denklemde yerine yazalım. 3 k.3 12 0 9 3k 12 0 3k 3 0 k 1 dir. x .x 12 idi. x 4 tür. k x 1 4 5 buluruz. Cevap: A 22) 2 1 2 2 2 1 2 x 9x 3 0 denkleminin kökleri x ve x dir. Buna göre, x x toplamının değeri kaçtır? A) 75 B) 87 C) 92 D) 94 E) 103 ÇÖZÜM: 2 2 2 2 1 2 1 2 1 2 x x (x x ) 2x .x 9 2.( 3) 81 6 87 dir. Cevap: B 23) 2 1 2 1 2 x 6x 12 0 denkleminin kökleri x ve x dir. 1 1 Buna göre, toplamının değeri kaçtır? x x 1 5 A) B) 1 C) 2 D) E) 3 2 2 www.matematikkolay.net ÇÖZÜM: 2 1 1 2 1 2 1 1 x x 6 1 dir. Cevap: A x x x .x 12 2 24) 2 1 2 2 1 2 x 10x 5 0 denkleminin kökleri x ve x dir. Buna göre, x 10x 5 ifadesinin değeri kaçtır? A) 25 B) 50 C) 75 D) 100 E) 125 ÇÖZÜM: 1 2 1 1 2 1 1 2 1 1 1 2 1 2 Kökler toplamı 10 x ‘i denklemde yerine yazalım. x 10x 5 0 x 10x 5 olur. Sorulan ifadede x yerine 10x 5 yazarsak, 10x 5 10x 5 10 (x x ) olur. 100 buluruz. Cevap: D 25) 2 1 2 2 2 1 2 x 5x m 0 denkleminin kökleri x ve x dir. x x 24 olduğuna göre, m kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 ÇÖZÜM: 1 2 1 2 Kökler toplamı 5 1 2 1 2 1 1 2 (x x ) (x x ) 15 x x 3 tür. x x 5 idi. Taraf tarafa toplarsak 2x 8 x 4 tür. x 1 dir. Kökler çarpımı 4 ise , m 4 tür. Cevap: C 26) 2 2 x ax 1 b 0 denkleminin kökleri 1 ve t, x (1 2a)x 6 0 denkleminin kökleri 3 ve t olduğuna göre, a.b çarpımı kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 ÇÖZÜM: 1.denklemin kökler toplamı 1 t a dır. 2.denklemin kökler toplamı 3 t 1 2a dır. Taraf tarafa çıkarırsak 2 1 3a a 1 olur. 1.denklemin kökler çarpımı 1.t 1 b dir. 2.denklemin kökler çarpımı 3.t 6 dır. 1 1 b Taraf tarafa bölersek 1 b 2 3 6 b 3 tür. a.b 1.3 3 buluruz. Cevap: B 27) 2 (k 1)x (k 2)x 12 0 denkleminin simetrik iki kökü vardır. O halde, bu köklerin çarpımı kaçtır? A) 0 B) 1 C) 2 D) 3 E) 4 ÇÖZÜM: 1 2 2 Simetrik kök x x dir. Yani toplamları 0 dır. k 2 0 olmalıdır. O halde k 2 dir. k 1 3x 12 0 şeklinde bir denklem var dır. 12 Kökler çarpımı 4 tür. Cevap : E 3 28) 2 2 2 2 2 Köklerinden biri 2 5 olan rasyonel katsayılı ikinci dereceden denklem aşağıdakilerden hangisidir? A) x 5x 1 0 B) x 4x 1 0 C) x 3x 4 0 D) x 6x 2 0 E) x 3x 2 0 ÇÖZÜM: 1 2 2 1 2 1 2 Rasyonel katsayılı olduğu için, diğer kök 2 5 tir. Kökler toplamı 2 5 2 5 4 tür. Kökler çarpımı (2 5)(2 5) 4 5 1 dir. Kökleri x ve x olan bir denklemi x (x x ) x .x 0 olarak yazabiliriz. Buna göre, 2 denklem x 4x 1 0 dır. Cevap: B www.matematikkolay.net 29) 2 1 2 1 2 2 2 2 2 x 4x 8 0 denkleminin kökleri x ve x dir. 1 1 Buna göre, kökleri 3 ve 3 olan ikinci dere – x x ceden denklem aşağıdakilerden hangisidir? A) x 13x 8 0 B) 6x 17x 24 0 C) 4x 21x 8 0 D) 3x 23x 74 0 2 E) 8x 52x 85 0 ÇÖZÜM: 1 2 1 2 4 2 1 1 2 1 2 8 1 2 1 2 1 2 -4 x x 4 ve x .x 8 dir. Yeni denklemin kökler toplamı 1 1 x x 1 13 6 6 6 dir. x x x .x 2 2 Kökler çarpımı ise 1 1 1 1 1 3 3 3 9 x x x .x x x 1 1 3 9 8 2 1 3 1 12 13 85 9 9 9 d 8 2 8 8 8 2 2 2 1 ir. Yeni denklem, 13x 85 x 0 dır. 8 ile her tarafı çarpalım. 2 8 8x 52x 85 0 olur. Cevap: E (Karmaşık Sayı Bilgisi Gerekli) x 4x 8 0 =16 4.1.8 16 dır. 4 16 4 4i x 2 2 II.Yol : 2 1 2 2i 2 2 2 2 2 2i dir. x 2 2i dir. 1 1 2 2i 1 i 13 i 3 3 3 3 tür. x 2 2i 8 4 4 4 4 13 i Diğer kök de tür. 4 4 13 Kökler toplamı dir. 2 13 1 169 1 170 85 Kökler çarpımı dir. 4 4 16 16 8 13 85 x x 0 8x 52x 85 2 8 0 olur. 30) 2 2 Gerçek katsayılı x mx n 0 denkleminin kök – lerinden biri 3 i dir. Buna göre, x (m 1)x n 0 denkleminin çözüm kümesi aşağıdakilerden hangisidir? A) {3i, 5i} B) {2 i, 5 i} C) {4, 6} D) {2, 5} E) {2, 4} ÇÖZÜM: Gerçek katsayılı ikinci derece denklemin bir kökü karmaşık sayı ise, diğer kök eşleniğidir. Yani diğer kök 3 i dir Kökler toplamı 3 i 3 i 6 dır. m 6 dır. Kökler çarpımı (3 i)(3 i) 9 1 10 dur. 2 ( 5)( 2) n 10 dur. Diğer denklem, x 7x 10 0 olur. (x 5)(x 2) 0 Ç.K {2, 5} tir. Cevap: B
Sayfalar: 1 2 3

“2.Dereceden Denklemler” üzerine 21 yorum

  3. Siteniz çok güzel ve yararlı yukarda her paylaştığınızın altına ”daha kaliteli sorular paylaşabilirsiniz” yazan arkadaşla muhattap bile olmayın. Çok meraklıysa tonlarca site var oraya gitsin. Elinize emeğinize sağlık =)

  6. 2t. soru hatali iki kare farkini 24 diye vermissini ama 15 olarak açmişsiniz

    onun disinda sorulariniz guzel kaliteli ama biraz daha zor sorsaniz sevinirim

    • Uyarınız için teşekkürler. Çözüm doğru ama cevap anahtarı yanlış işaretlenmişti. Şimdi düzeltildi.

  15. VALLA EMEĞİNİZE SAĞLIK İYİKİ VARSINIZ SAÇMA SAPAN YORUM YAZANLARA BAKMAYIN MÜKEMMELSİNİZ =)

Yorum yapın