2.Dereceden Denklemler

1.Sayfa için Tıklayınız.

11.SORU

Çözüm için Tıklayınız.

12.SORU


Çözüm için Tıklayınız.

13.SORU

Çözüm için Tıklayınız.

14.SORU

Çözüm için Tıklayınız.

15.SORU

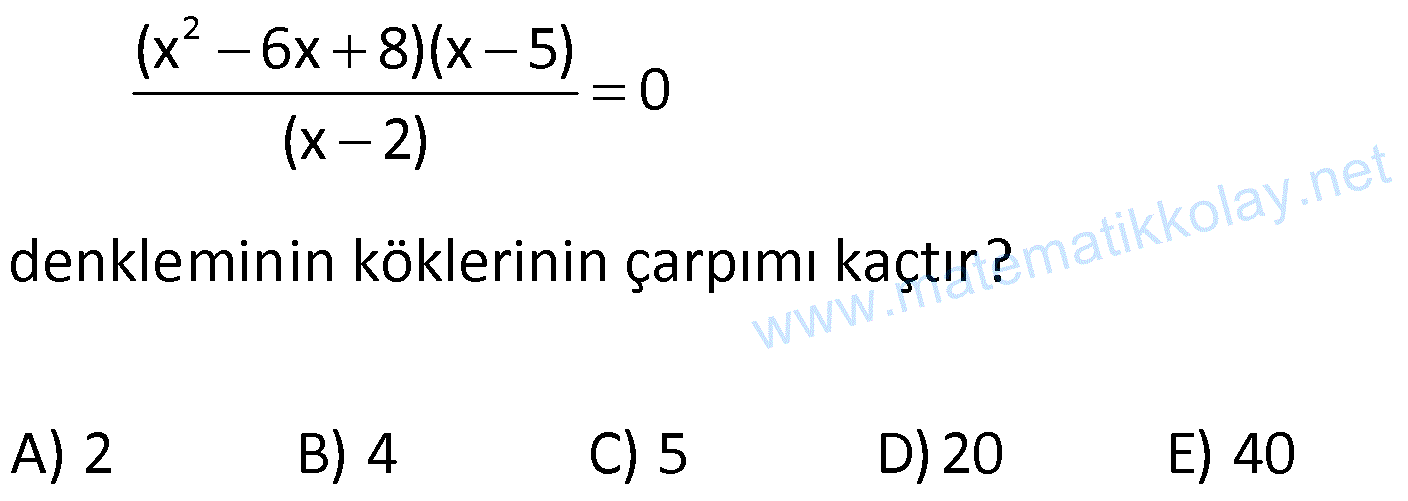
Çözüm için Tıklayınız.

16.SORU

Çözüm için Tıklayınız.

17.SORU

Çözüm için Tıklayınız.

18.SORU

Çözüm için Tıklayınız.

19.SORU

Çözüm için Tıklayınız.

20.SORU

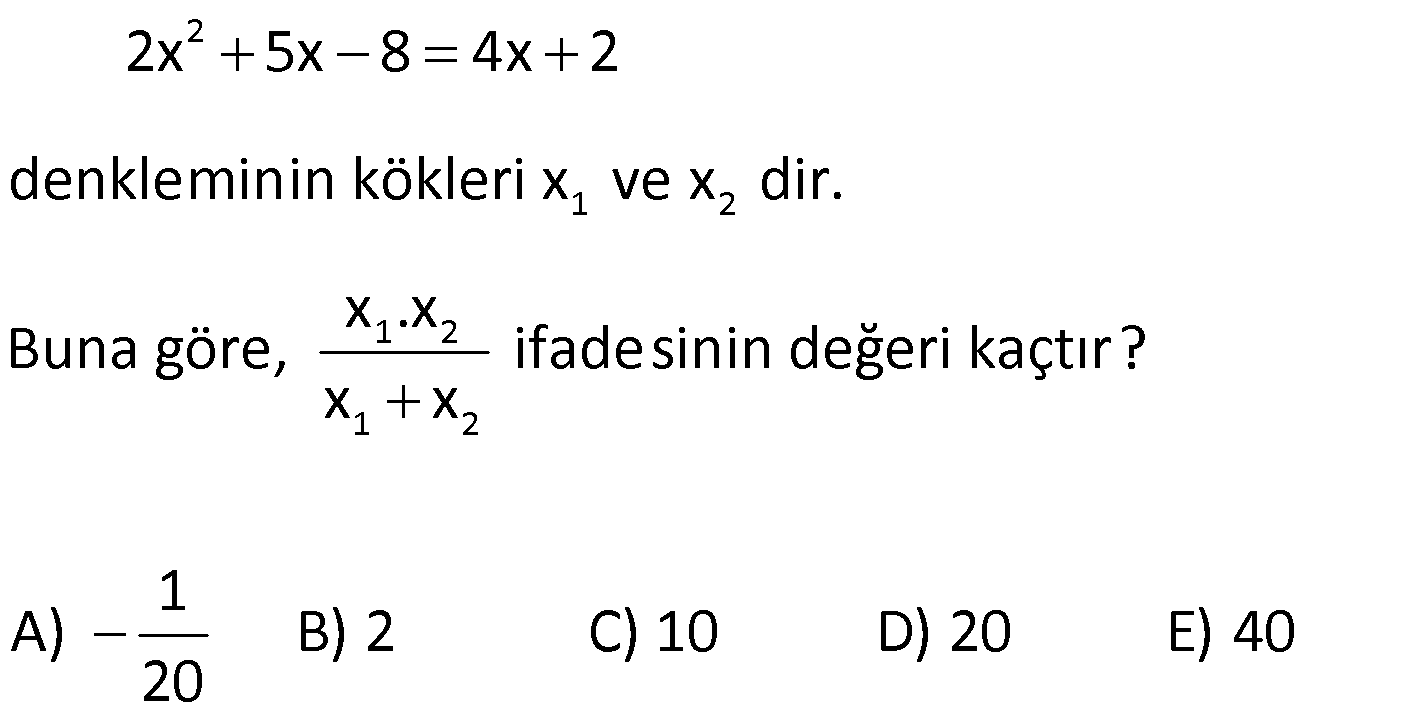
Çözüm için Tıklayınız.

3.Sayfa için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
11) 2 x 4x a 5 0 denkleminin reel kökü olmadığına göre, a’nın değer aralığı aşağıdakilerden hangisidir? A) 1,1 B) , 1 C) , 1 D) 1, E) 1,     ÇÖZÜM: 2 0 olmalıdır. b 4ac 0 16 4.1.(a 5) 0 16 4(a 5) 4 a 5 1 a a 1, dur. Cevap: E         12) 2 2 2x 7x m 0 3x 5x 4m 0 denklemlerinin birer kökleri eşit olduğuna göre, farklı olan köklerinin toplamı kaçtır? m 0 2 1 3 4 5 A) B) C) D) E) 3 2 4 7 6  www.matematikkolay.net ÇÖZÜM: 2 2 2 2 2 Birer kökleri eşit olduğunda, x li terimleri yok ede – cek şekilde ortak çözüm yapılmalıdır. 3 / 2x 7x m 0 2 / 3x 5x 4m 0 6x 21x 3m 0 6x 10x 8m 0 11x 11m 0 x m d 2 2 m 4 2 2x x ir. Demek ki ortak kökleri m’ye eşitmiş. Denklemlerden birinde yerine yazalım. 2m 7m m 0 2m 6m 0 2m(m 3) 0 m 3 tür. m’nin 0’a eşit olmadığı soruda verilmişti. O halde 1.denklem 2x 1 3 1 x 2 2 3x 4 x 3 4 x 3 7x 3 0 1 (2x 1)(x 3) 0 Farklı kök x dir. 2 2.denklem 3x 5x 12 0 4 (3x 4)(x 3) 0 Farklı kök x tür. 3 1 4 3 8 5 Toplamları dır. Cevap : E 2 3 6 6 13) 2 2 (m 2)x 7x n 0 3x (m 2)x 6 0 denklemlerinin çözüm kümeleri birbirine eşit oldu – ğuna göre, m n toplamı en çok kaçtır? A) 11 B) 8 C) 1 D) 1 E) 6 ÇÖZÜM: 2 2 Çözüm kümeleri aynı ise, katsayıları oranı birbirine eşit olmalıdır. m 2 7 m 4 21 m 25 3 m 2 m 5 ya da m 5 tir. 7 m 5 olursa katsayılar orasındaki oran olur. 3 7 n n 14 olur. 3 6 m n 5 ( 14) 11 olur. m 5 olursa katsayılar orasındaki oran 1 olur. n 1 n 6 olur. 6 m n 5 6 1 olur. Cevap: D 14) 3 2 x 3x 4x 12 0 denkleminin çözüm kümesi aşağıdakilerden hangisi – dir? A) 3, 2, 2 B) 2, 1, 2 C) 2, 2 D) 1, 0, 2 E) 0, 2, 4 ÇÖZÜM: 2 2 x 3 x 2 x 2 Denklem, 3.dereceden bir denklemdir. Ancak çarpanlarına ayırarak, 2.dereceden denklemde olduğu gibi köklerini bulabiliriz. x (x 3) 4(x 3) 0 (x 3)(x 4) 0 (x 3)(x 2)(x 2) 0 Ç.K 3, 2, 2 dir. Cevap: A 15) 2 (x 6x 8)(x 5) 0 (x 2) denkleminin köklerinin çarpımı kaçtır? A) 2 B) 4 C) 5 D)20 E) 40 www.matematikkolay.net ÇÖZÜM: ( 4).( 2) x 4 x 2 x 5 2 x 2 olamaz. Kesirli bir ifade 0’a eşitse, pay 0 dır ama payda 0 olamaz. Verilen ifadeyi çarpanlarına ayıralım. (x 6x 8 )(x 5) (x 4)(x 2)(x 5) 0 0 (x 2) (x 2) Kökler 4 ve 5 tir. Çarpıml arı 20 olur. Cevap : D 16) x 1 x 2 2 5 0 x x 1 denkleminin çözüm kümesi aşağıdakilerden hangisidir? A) { 3, 2} B) { 1, 2} C) { 2, 1} D) { 4, 1} E) {0, 2} ÇÖZÜM: Burası 0 olmalı 2 2 2 2t 1 t 2 1 t 2 Değişken değiştirerek, denklemi 2.dereceden denk – lem olarak çözebiliriz. x 1 t olsun. x 2 2t 5 0 şeklinde denklem olur. t 2t 2 5t 0 t 2t 2 5t 0 2t 5t 2 0 (2t 1) t 2 (t 2) 0 dır. 1 x 1 1 t olursa 2x 2 x x 2 dir. 2 x 2 x 1 t 2 olursa 2 x 1 2x x 1 dir. x Ç.K 2, 1 dir. Cevap: B 17) x x 9 6.3 27 0 denkleminin gerçek sayılardaki çözüm kümesi aşağıdakilerden hangisidir? A) {2} B) { 1, 2} C) { 2, 1} D) { 1} E) {0, 2} ÇÖZÜM: x 2 t 9 t 3 x x 3 t olsun. t 6t 27 0 şeklinde denklem olur. (t 9)(t 3) 0 t 9 veya t 3 tür. t 9 olursa 3 9 x 2 dir. t 3 olursa 3 3 gerçek kök yok. Ç.K 2 dir. Cevap: A 18) x 6 3 x 1 denkleminin gerçek sayılardaki çözüm kümesi aşağıdakilerden hangisidir? A) { 5} B) { 5, 2} C) {2, 5} D) { 2} E) { 2, 5} ÇÖZÜM: 2 2 x 5 x 2 x 6 x 4 tür. İki tarafın da karesini alalım. x 6 x 8x 16 0 x 7x 10 0 (x 5)(x 2) x 5 veya x 2 dir. Ancak, kare alarak çözüm yapınca ekstra bir kök gelmiş olabilir. Bu yüzden her kökü yerine yazıp test etmek gerekiyor. x 5 yazarsak 5 6 5 4 1 1 hatalı Demek ki x 5 olamaz. x 2 yazarsak 2 6 2 4 4 2 doğru Demek ki x 2 olabilir. Ç.K 2 dir. Cevap: D www.matematikkolay.net 19) 2 (x 2) 4x 8 21 0 denkleminin gerçek sayılardaki çözüm kümesi aşağı – dakilerden hangisidir? A) { 5} B) { 5, 1} C) { 1, 5} D) {9} E) { 5, 9} ÇÖZÜM: 2 2 2 2 t 7 t 3 t 7 t 3 (x 2) nin yerine x 2 yazabiliriz. 4x 8 4 x 2 olarak yazabilir. O halde, denklem x 2 4 x 2 21 0 olur. x 2 t diyelim. t 4t 21 0 (t 7)(t 3) 0 x 2 7 olursa x 2 7 x 9 dur veya x 2 7 x 5 tir. x 2 3 olamaz. Kök yok. Cevap: E 20) 2 1 2 1 2 1 2 2x 5x 8 4x 2 denkleminin kökleri x ve x dir. x .x Buna göre, ifadesinin değeri kaçtır? x x 1 A) B) 2 C) 10 D) 20 E) 40 20 ÇÖZÜM: 2 2 2 1 2 1 2 1 2 1 2 ax bx c 0 denkleminde b c Kökler toplamı Kökler çarpımı dır. a a 2x 5x 8 4x 2 2x x 10 0 1 x x dir. 2 10 x .x 5 tir. Buna göre, 2 x .x 5 10 dur. Cevap: C x x 1 2
Sayfalar: 1 2 3

“2.Dereceden Denklemler” üzerine 21 yorum

  3. Siteniz çok güzel ve yararlı yukarda her paylaştığınızın altına ”daha kaliteli sorular paylaşabilirsiniz” yazan arkadaşla muhattap bile olmayın. Çok meraklıysa tonlarca site var oraya gitsin. Elinize emeğinize sağlık =)

  6. 2t. soru hatali iki kare farkini 24 diye vermissini ama 15 olarak açmişsiniz

    onun disinda sorulariniz guzel kaliteli ama biraz daha zor sorsaniz sevinirim

    • Uyarınız için teşekkürler. Çözüm doğru ama cevap anahtarı yanlış işaretlenmişti. Şimdi düzeltildi.

  15. VALLA EMEĞİNİZE SAĞLIK İYİKİ VARSINIZ SAÇMA SAPAN YORUM YAZANLARA BAKMAYIN MÜKEMMELSİNİZ =)

Yorum yapın