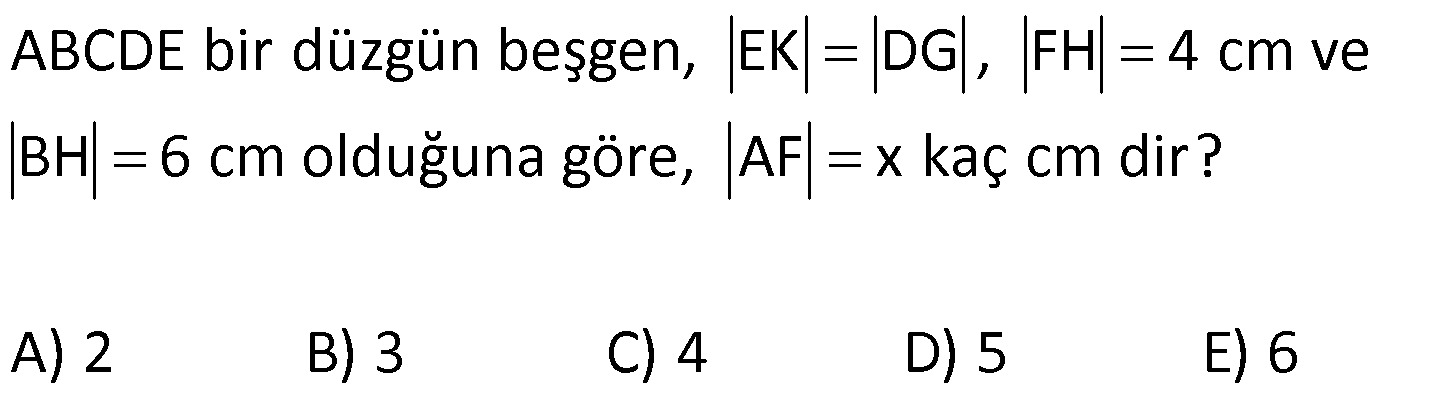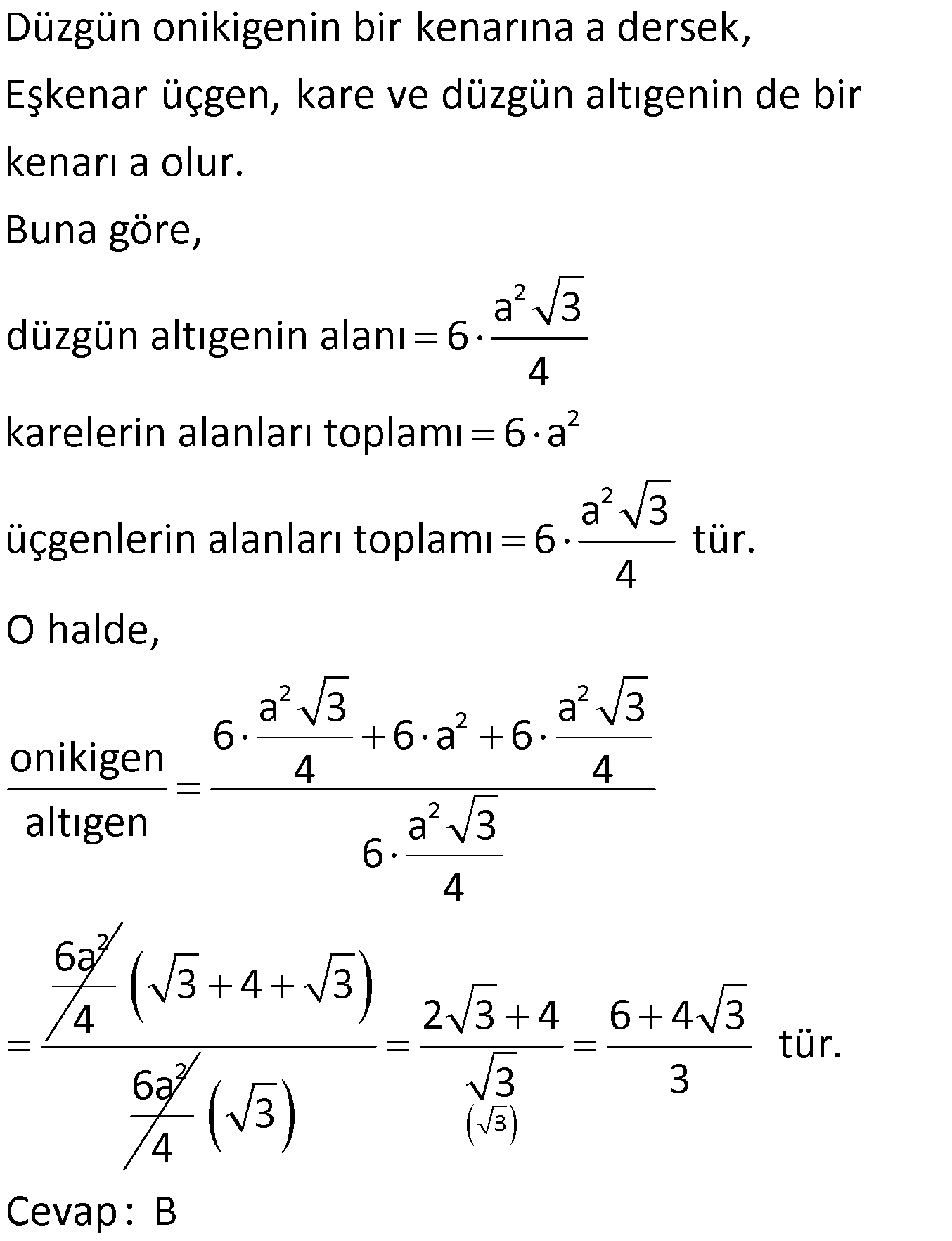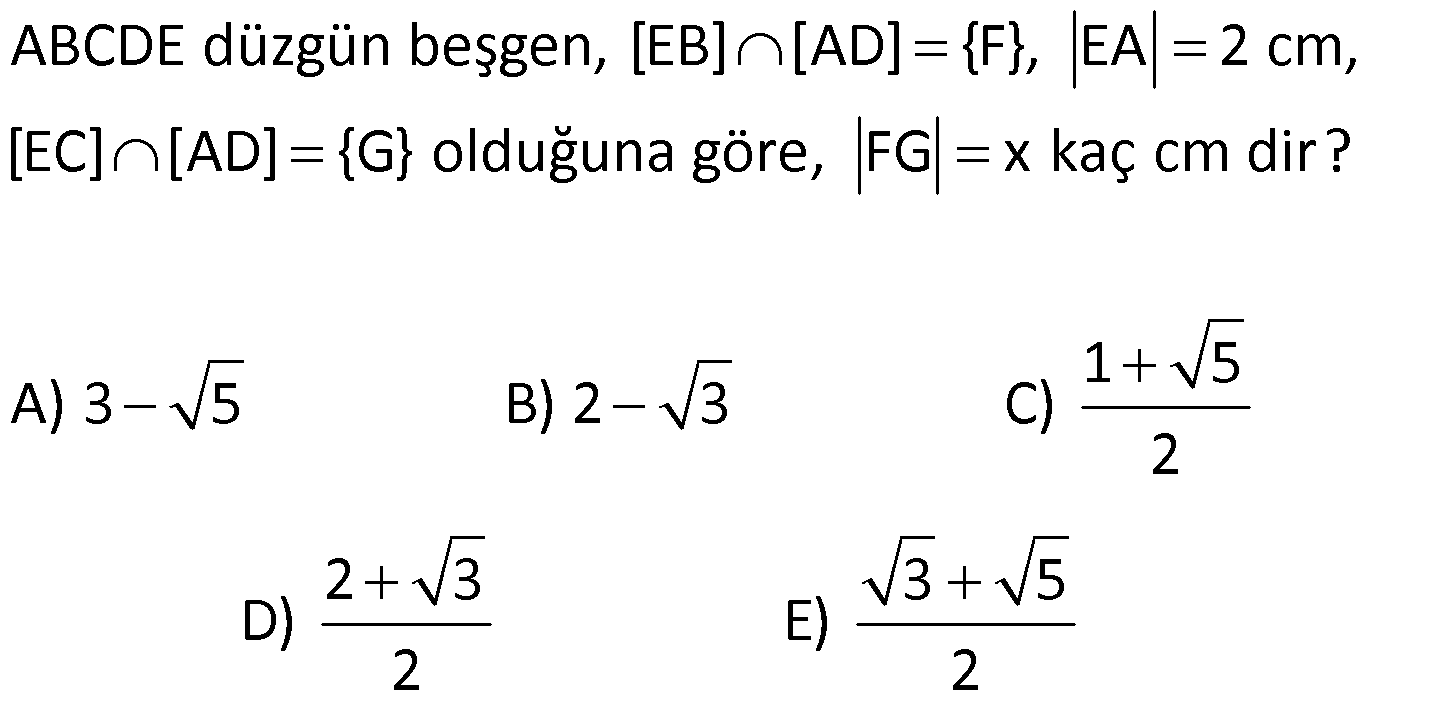Soru Sor sayfası kullanılarak Çokgenler konusu altında Nitelikli Çokgen Soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
 |  |  |  |  |
Çözüm için Tıklayınız.
2.SORU
| | | | | |
Çözüm için Tıklayınız.
3.SORU
| | | | | |
Çözüm için Tıklayınız.
4.SORU
| | | | | |
Çözüm için Tıklayınız.
5.SORU
| | | | | |
Çözüm için Tıklayınız.
6.SORU
| | | | | |
Çözüm için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
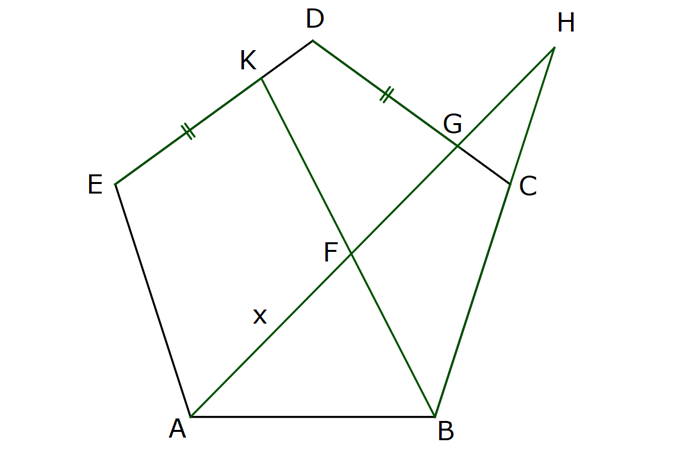
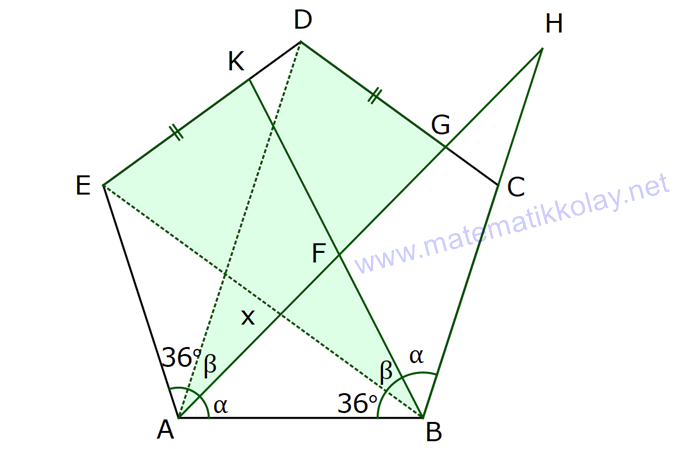
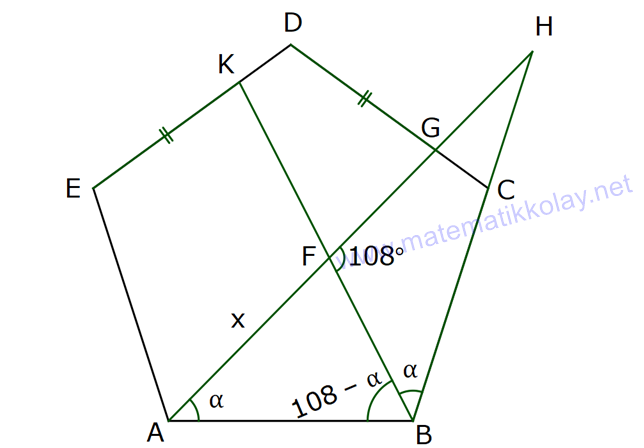
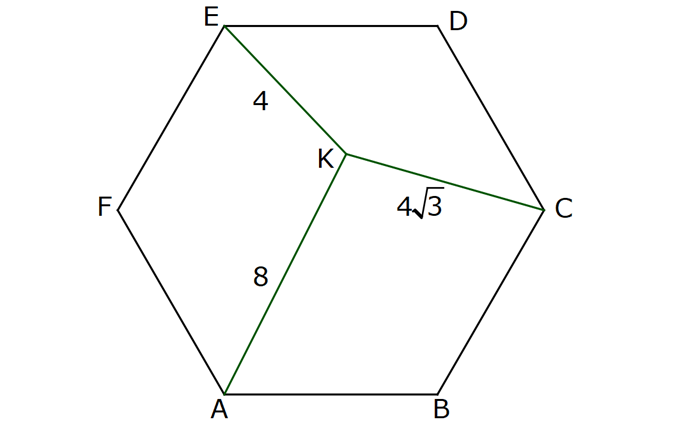
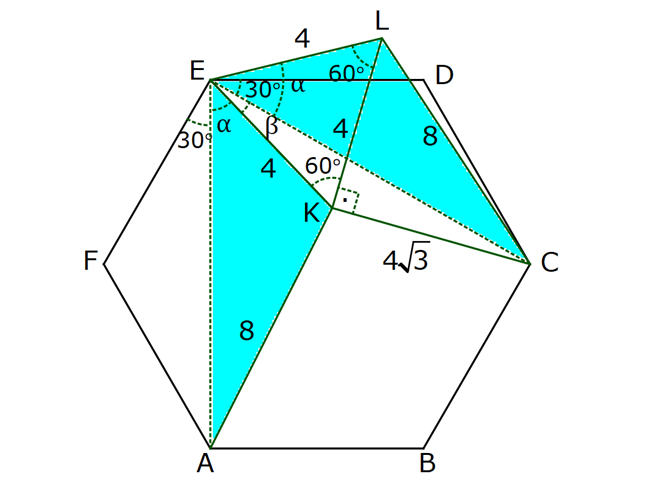
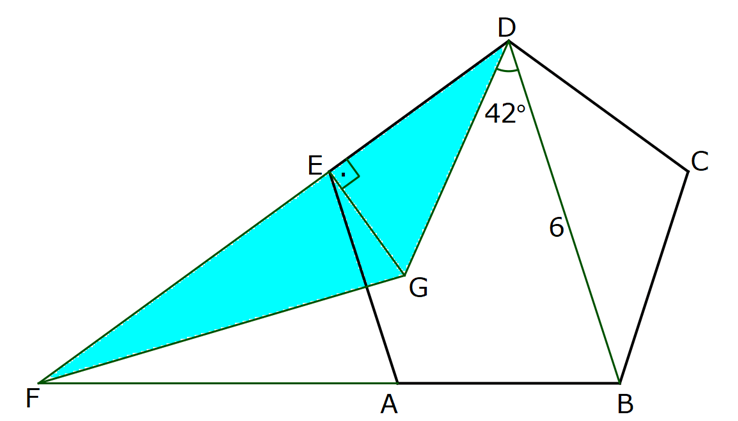
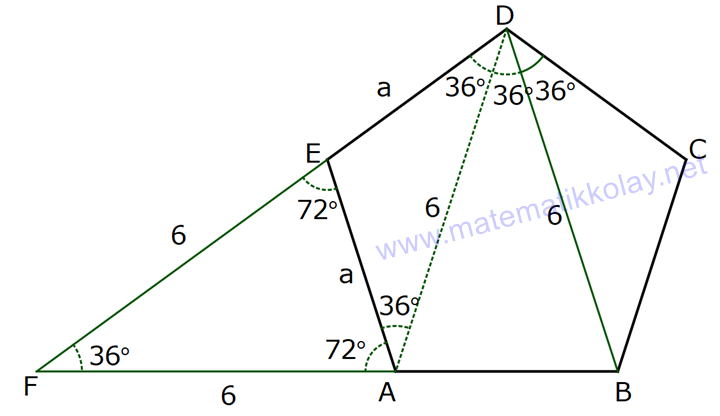
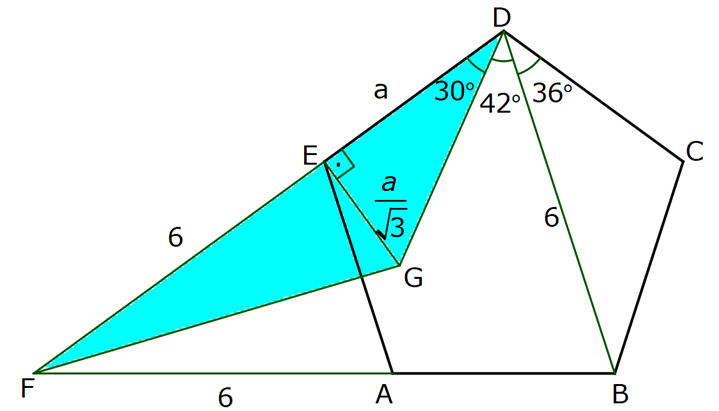
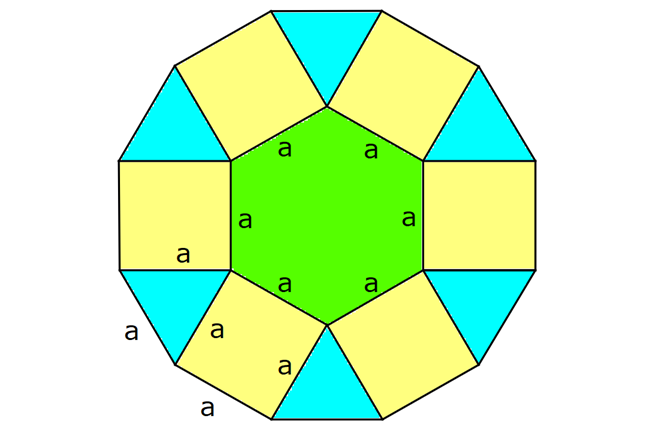
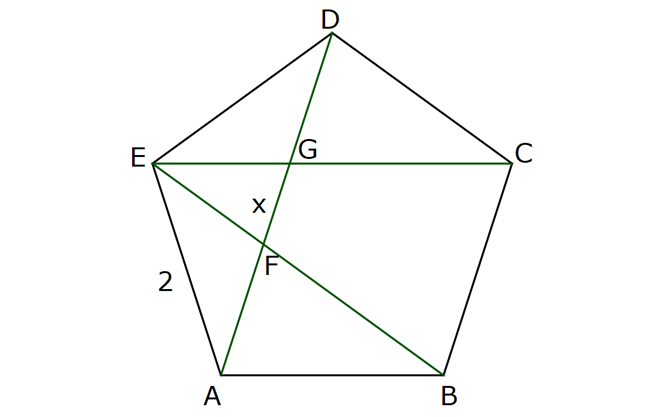
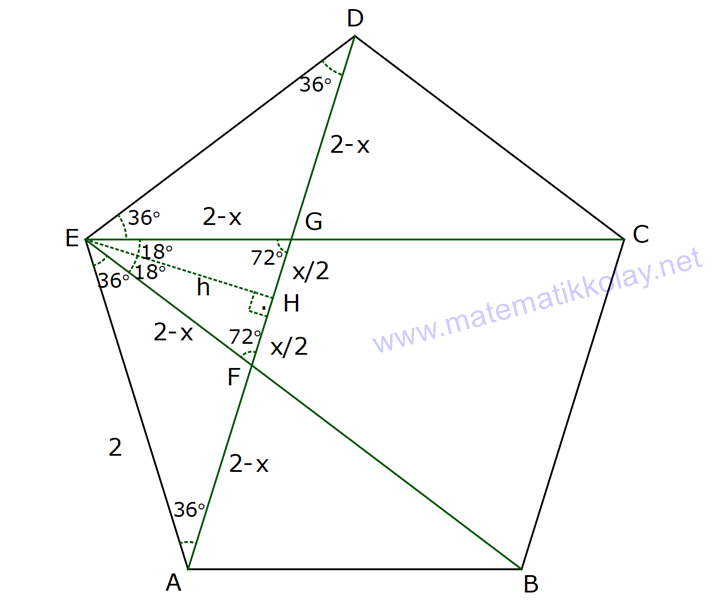
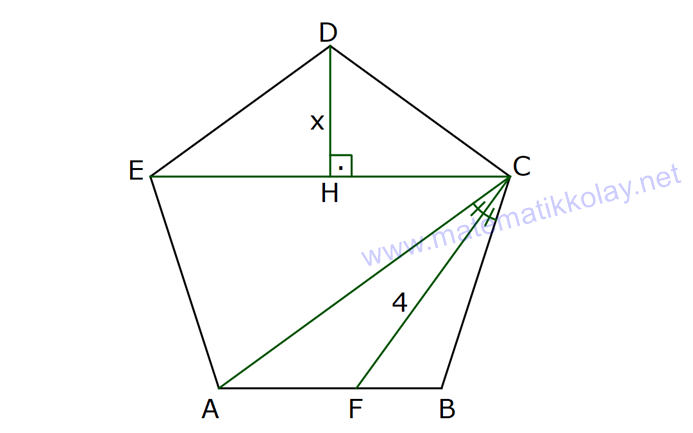
NİTELİKLİ ÇOKGEN SORULARI www.matematikkolay.net 1) ABCDE bir düzgün beşgen, EK DG , FH 4 cm ve BH 6 cm olduğuna göre, AF x kaç cm dir? A) 2 B) 3 C) 4 D) 5 E) 6 ÇÖZÜM: EB ve AD doğrularını çizersek, EBK üçgeni ile DAG üçgenlerinin eş olduğunu görürüz. Çünkü kenarları birbirine eşit üçgenlerdir. m(EAD) m(ABE) 36 dir. (Beşgenden dolayı) m(DAG) m(EBK) olsun. (Eş üçgenl erdi) m(BAH) m(KBH) eşittir. (108 den geriye kalan açı) m(BAH) m(KBH) diyerek soruyu ilerletelim. m(ABK) 108 dır. m(BFH) 108 108 dir. Buna göre, AHB üçgeni ile BHF üçgeni arasında benzerlik vardır. Çünkü tüm açıları aynıdır. AHB x 4 6 AH HB BHF BH HF 6 4 4x 16 36 4x 20 x 5 cm dir. Cevap: D 2) 2 ABCDEF bir düzgün altıgen, AK 8 cm, EK 4 cm ve KC 4 3 cm olduğuna göre, düzgün altıgenin alanı kaç cm dir? A) 42 3 B) 48 3 C) 56 3 D) 60 3 E) 64 3 ÇÖZÜM: www.matematikkolay.net EA köşegeni ile EC köşegeni eşittir. İkisinde 4 cm olan kenar vardır İlk önce EKL eşkenar üçgenini oluşturalım. Her bir iç açısı 60 dir. Sonra [LC] yi çizelim. ELC üçgeni ile EKA üçgeni eş üçgen olurlar. . Köşegen ile 4 cm arasındaki açı ikisinde de dır. Bu sebeple LC 8 cm olur. LKC üçgeninde kenarlar 4 – 4 3 8 cm oldu. Bu bir 30 – 60 – 90 üçgenidir. Dolayısıyla LKC açısı 90 dir. m(EKC) 150 oldu. EC uz 2 2 2 2 unluğunu kosinüs teoremiyle hesaplayalım. EC 4 (4 3) 2.4.4 3 cos150 EC 16 48 2 3 .4.4 3. 2 2 2 2 EC 64 48 EC 112 EC 112 4 7 cm dir. Eşit uzunlukta olduğu için EA 4 7 cm dir. FEA üçgeni 30 – 30 -120 üçgenidir. Altıgenin bir kenarına a dersek, EA a 3 olur. 4 7 a 3 4 7 a cm olur. 3 4 7 a 3 3 Altıgenin alanı 6 6 4 2 3 4 6 2 16 4 7 3 3 4 2 56 3 cm dir. Cevap : C 3) www.matematikkolay.net 2 ABCDE bir düzgün beşgen, DB 6 cm, m(BDG) 42 [GE] [DF] ve F,A,B doğrusal olduğuna göre, A(DGF) kaç cm dir? A) 6 2 B) 3 10 C) 4 6 D) 10 E) 6 3 ÇÖZÜM: Düzgün beşgenin tüm köşegenleri birbirine eşittir. Dolayısıyla AD 6 cm dir. Yukarıdaki şekildeki gibi açıları yazarsak, FDA üçgeninin ikizkenar olduğunu görürüz. Dolayısıyla FA 6 cm olur. Aynı şekilde F EA üçgeni de ikizkenardır. EF 6 cm olur. Beşgenin bir kenarına a diyelim. EA // DB olduğundan benzerlik uygulayabiliriz. EAF DFB dir. a 6 a(6 a) 36 dır. Şimdi böyle bırakalım. 6 6 a 36 BDG açısı 42 verildiğinden, EDG açısına 30 kalır. EDG üçgeni bir 30 – 60 – 90 üçgeni olur. a O halde, EG tür. 3 a (a 6) 3 (a 6).a 36 A(DGF) 2 2 3 18 2 3 18 3 3 18 6 3 3 2 6 3 cm dir. Cevap : E 4) Yukarıda verilen düzgün onikigenin içine düzgün altıgen, kare ve eşkenar üçgenler çizilmiştir. Buna göre, düzgün on ikigenin alanının, düzgün altıgenin alanına oranı kaçtır? 8 3 3 6 4 3 10 A) B) C) 3 3 5 3 3 3 6 3 9 3 D) E) 3 3 ÇÖZÜM: www.matematikkolay.net 2 2 Düzgün onikigenin bir kenarına a dersek, Eşkenar üçgen, kare ve düzgün altıgenin de bir kenarı a olur. Buna göre, a 3 düzgün altıgenin alanı 6 4 karelerin alanları toplamı 6 a üçgenlerin alanları t 2 2 2 2 2 2 a 3 oplamı 6 tür. 4 O halde, a 3 a 3 6 6 a 6 onikigen 4 4 altıgen a 3 6 4 6a 4 2 3 4 3 6a 4 3 2 3 4 6 4 3 tür. 3 3 3 Cevap : B 5) ABCDE düzgün beşgen, [EB] [AD] {F}, EA 2 cm, [EC] [AD] {G} olduğuna göre, FG x kaç cm dir? 1 5 A) 3 5 B) 2 3 C) 2 2 3 3 5 D) E) 2 2 ÇÖZÜM: www.matematikkolay.net E’den dikme indirelim. x uzunluğu iki eş parçaya ayrılır. Sonra açıları yazarak ikizkenar üçgenleri görebiliriz. EAG ikizkenardır. AG 2 cm dir. AF 2 x kalır. EFA ikizkenardır. EF 2 x olur. EFH üçgenin 2 2 2 2 2 2 2 2 2 2 2 2 2 2 de pisagordan, x h 2 x dir. 2 AEH üçgeninde pisagordan x x h 2 2 x 4 2 dir. 2 2 Bu ikisini birbirine eşitleyelim. x x 2 x 4 2 2 2 x x 4 4x x 4 4 2x 4 4 4 4x x 2 x 4 4 4 2 x 2x 4 2 2 9 5 2 2 2 4 4x x 2x x 6x 4 0 x 6x 9 5 0 x 6x 9 5 (x 3) 5 x 3 5 x 3 5 x 3 5 olamaz. Çünkü 2’den küçük olmalı. x 3 5 cm dir. Cevap : A 6) ABCDE düzgün beşgen, [DH] [EC], [CF] açıortay, CF 4 cm olduğuna göre, DH x kaç cm dir? 3 5 A) 1 B) C) 2 D) E) 3 2 2 ÇÖZÜM: [EB] köşegenini çizelim. ABE üçgeni ile DEC üçgeni eş üçgenlerdir. Dolayısıyla AK x olur. [EB] açıortay olduğu için, AEG üçgeninde aynı zamanda kenarortaydır. Dolayısıyla AG 2x tir. Açıları yazdığımızda m( BEC) 36 ve m(ECT) 54 olur. Dolayısıyla m(ETC) 90 olur. O halde [AG] // [FC] dir. Çünkü ikisi de [EB] ye dik. Ayrıca [AB] ile [EC] de paraleldir. Buna göre, AG FC dir. 2x 4 x 2 cm buluruz. Cevap : C
