Soru Sor sayfası kullanılarak Çarpanlara Ayırma konusu altında Tam kare ifadelerden yararlanarak en büyük en küçük değer bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
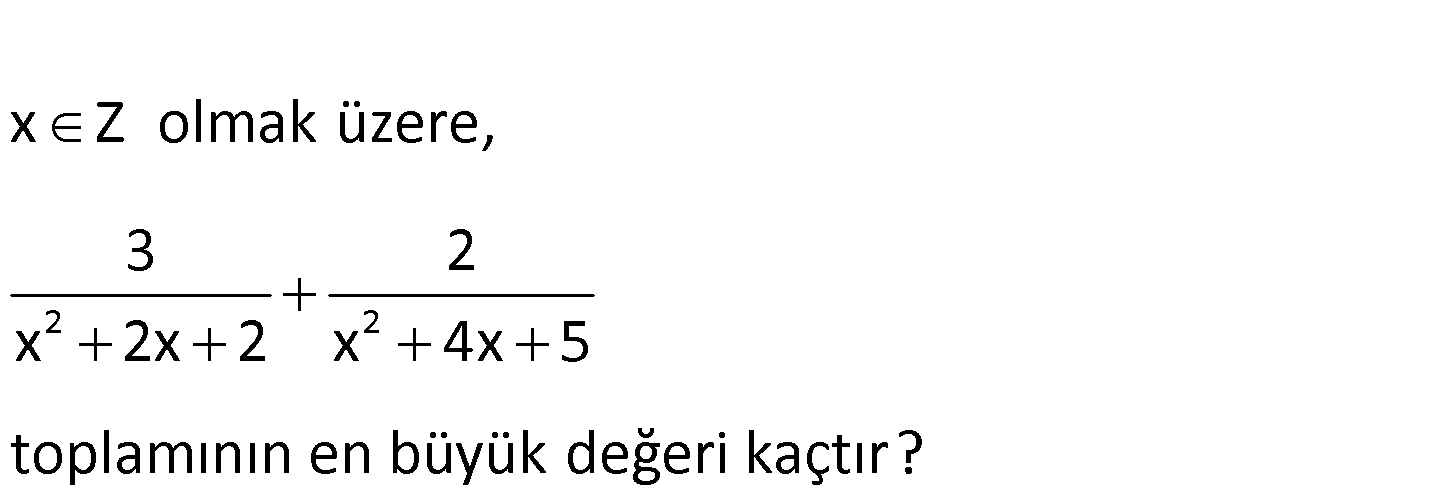

2.SORU

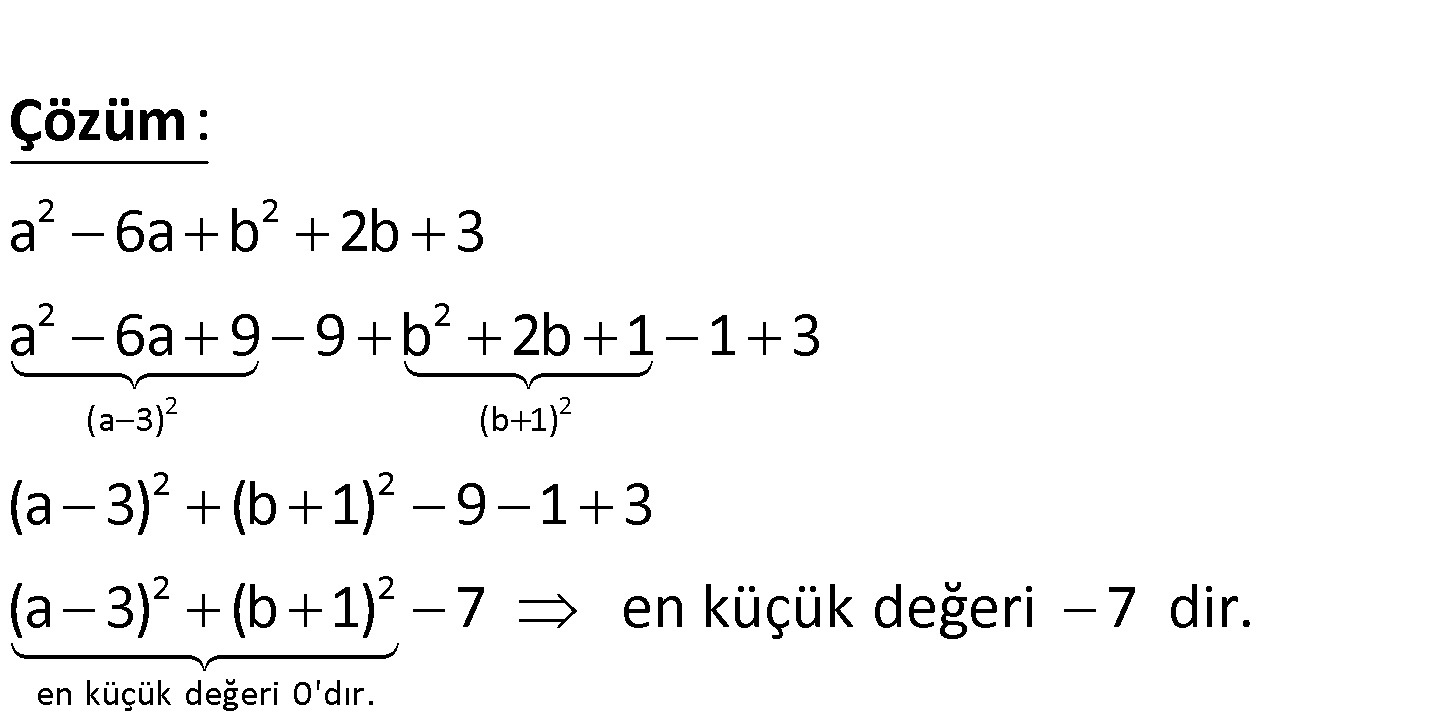
3.SORU
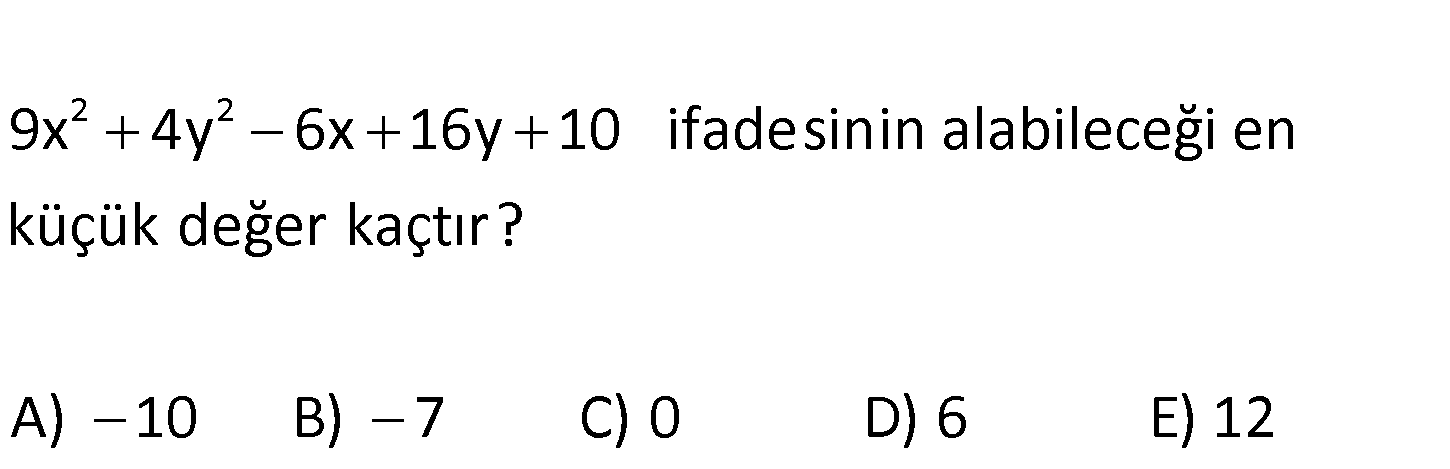
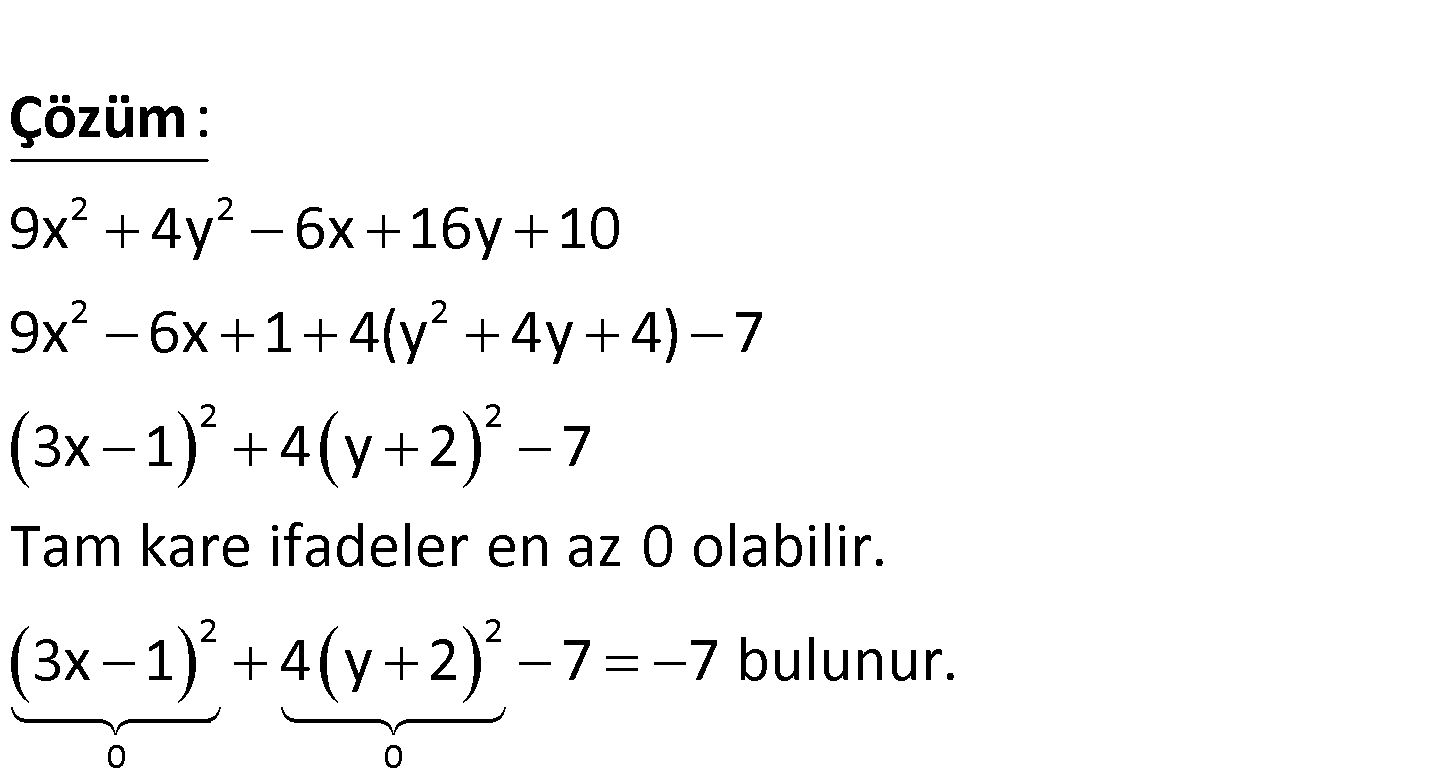
4.SORU

5.SORU


6.SORU


7.SORU


8.SORU

9.SORU


10.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net 2 2 x Z olmak üzere, 3 2 x 2x 2 x 4x 5 toplamının en büyü k değeri kaç ? tır 2 2 3 2 (x 1) 1 (x 2) 1 Tam kare ifadeyi en az 0 yapabiliriz. 3’ün olduğu kesrin paydasını en az y : Çözüm apmak, bu ifadenin en büyük olmasını sağlar. Bu sebeple x 1 seçmeliyiz. x 1 için; 3 2 3 1 4 buluruz. 1 2 39
2 2 a ve b reel sayılardır. a 6a b 2b 3 ifadesinin alabileceği en küçük değer kaçtır? A) 0 B) 4 C) 5 D) 7 E) 8 www.matematikkolay.net 2 2 2 2 2 2 (a 3) (b 1) 2 2 2 2 en k a 6a b 2b 3 a 6a 9 9 b 2b 1 1 3 (a 3) (b 1) 9 1 3 (a 3) (b 1 : ) Çözüm üçük değeri 0’dır. 7 en küçük değeri 7 dir. 54
2 2 9x 4y 6x 16y 10 ifadesinin alabileceği en küçük değer kaçtır? A) 10 B) 7 C) 0 D) 6 E) 12 www.matematikkolay.net 2 2 2 2 2 2 2 0 9x 4y 6x 16y 10 9x 6x 1 4(y 4y 4) 7 3x 1 4 y 2 7 Tam kare ifadeler en az 0 olabilir. 3x 1 : Çözüm 2 0 4 y 2 7 7 bulunur. 102
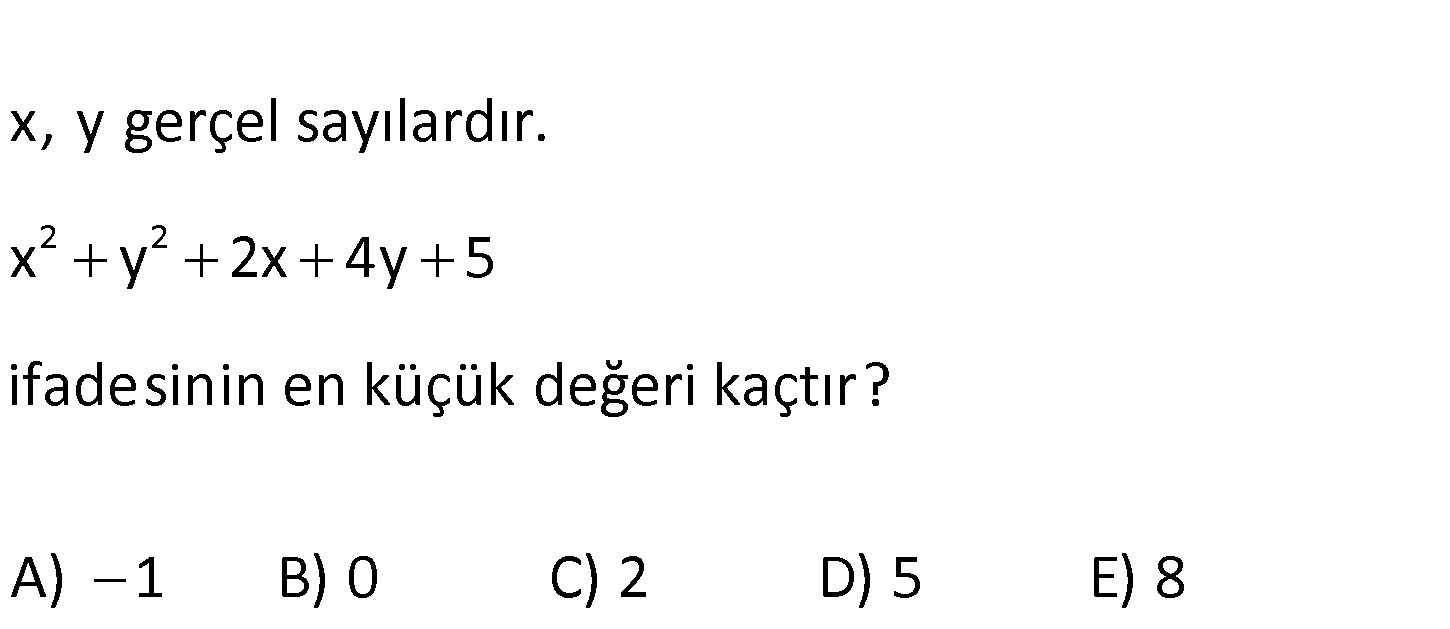
www.matematikkolay.net 2 2 x, y gerçel sayılardır. x y 2x 4y 5 ifadesinin en küçük değeri kaçtır? A) 1 B) 0 C) 2 D) 5 E) 8 2 2 2 2 2 2 x y 2x 4y 5 x 2x 1 y 4y 4 x 1 y 2 Tam kare ifadeler en az 0 olabilir. 0 0 0 buluruz. en : ( Çözüm küçük) 104
2 2 a ve b birer reel gerçel sayılardır. Buna göre; a b 8a 4b 32 ifadesinin alabileceği en k üçük değer kaçtır? A) 6 B) 8 C) 10 D) 12 E) 14 www.matematikkolay.net 2 2 2 2 2 2 (a 4) (b 2) a b 8a 4b 32 32′ yi 16 4 12 şeklinde parçalayalım a 8a 16 b 4b 4 12 : Çözüm 2 2 2 2 0 0 (a 4) (b 2) 12 Tam kare ifadeler, en az 0 olabilir. (a 4) (b 2) 12 En küçük değeri 12 dir. 122
2 2 x 4 y 5 ifadesini en küçük yapan x ve y değerlerinin çarpı – mı kaçtır? A) 20 B) 16 C) 25 D) 20 E) 30 Tam kare ifadeler negatif olamaz. En küçük 0 olabilir. Bu sebeple tam karenin içerisini : 0 yap Çözüm an x ve y değerlerini almalıyız. x 4 0 x 4 y 5 0 y 5 tir. Çarpımları 4.5 20 buluruz. 151
2 2 4x 5y 12y 4xy 14 ifadesinin alabileceği en küçük değer kaçtır? A) 0 B) 5 C) 6 D) 9 E) 1 6 2 2 2 2 y 4y 2 2 2 2 2 : Tam kare ifade elde etmeye çalışalım. 4x 5y 12y 4xy 14 4x y 4y 12y 4xy 14 4x 4xy y Çözüm 2 2 2 9 5 2x y 2 2 2y 3 2 2 2 2 En az 0 En az 0 4y 12y 14 2x y 4y 12y 9 5 2x y 2y 3 5 Tam kare ifadeler, negatif olamayacağı için en az 0 olabilir. 2x y 2y 3 5 En az 5 olabilir. 193
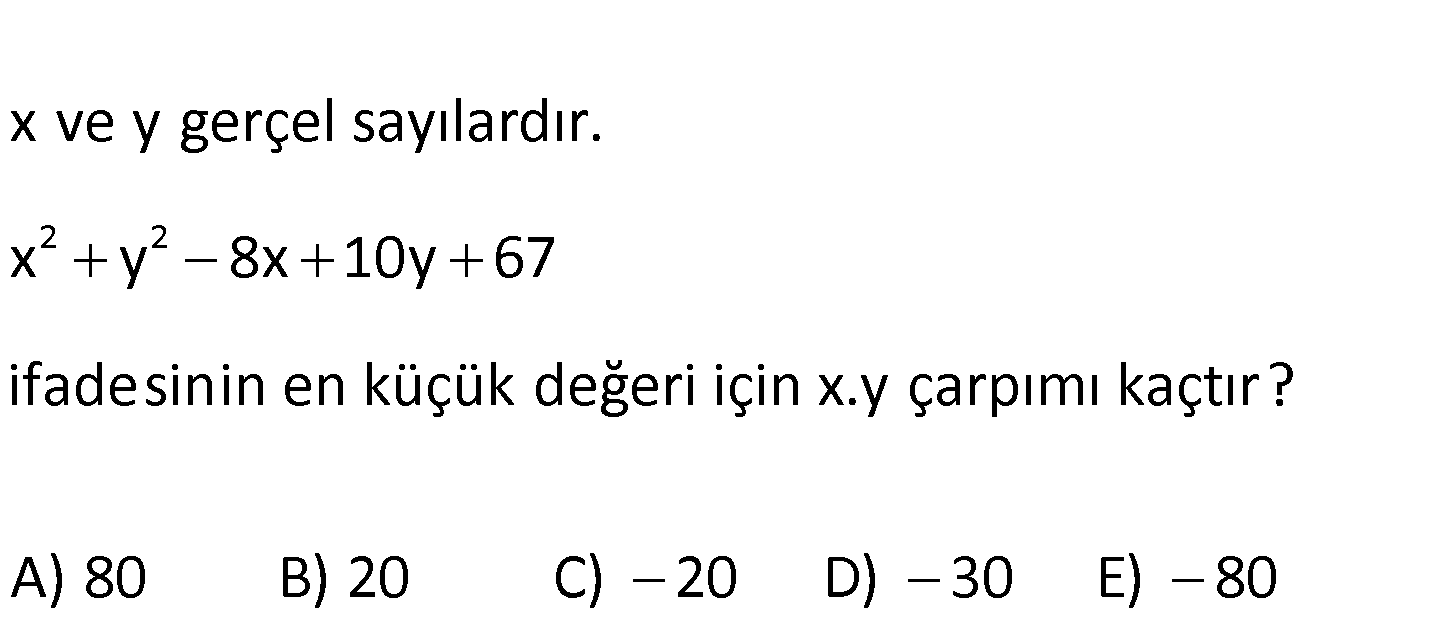
2 2 x y 8x 10y 67 ifadesinin en küçük değeri iç x ve y gerçel in x.y çarpımı s k ayılard açtır? A ı ) r. 80 B) 20 C) 20 D) 30 E) 80 2 2 2 2 x y 8x 10y 67 Tam kare ifadeler, elde etmeye çalışalım. x 8x 16 y 10y 25 67 16 25 şekli : Çözüm 2 2 2 2 x 4 y 5 2 2 Burayla işimiz yok. nde yazabiliriz. x 8x 16 y 10y 25 67 16 25 x 4 y 5 67 16 25 Bu ifadeyi en küçük yapmak için; x 4 ve y 5 vermeliyiz. Çünkü tam kare ifadeler en az 0 ol abilir. O halde; x.y 4. 5 20 buluruz. 196
2 2 x pozitif bir reel sayıdır. 9 32x 8x ifadesinin alabileceği en küçük değer kaçtır? A) 4 B) 6 C) 8 D) 10 E) 12 www.matematikkolay.net 2 2 32x ifadesi 4 2x in karesidir. 9 3 ifadesi in karesidir. 8x 2 2x Bu iki sayının farkını ka : n Çözüm 2 2 2 2 2 resine bakarak, en küçük değeri bulabiliriz. 3 3 9 4 2x 32x 2.4 2x 2 2x 2 2x 8x 3 4 2x 32x 2 2 2x .4 2 x 3 2 2 x 2 2 2 2 En az 0 olabilir. 2 2 2 2 9 8x 3 9 4 2x 32x 12 2 2x 8x 9 0 32x 12 8x 9 12 32x En küçük değeri 12 dir. 8x 208
2 f x x 4x 7 fonksiyonun alabileceği en küçük değer kaçtır? 2 2 2 2 f(x) x 4x 7 x 4x 4 3 (x 2) 3 (x 2) Tam kare ifadedir. Negatif olamaz. : Çözüm 2 0 En az 0 olabilir. Buna göre f(x) (x 2) 3 en az 3 olur. Cevap: 3

