Soru Sor sayfası kullanılarak Çarpanlara Ayırma konusu altında İki kare farkı ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
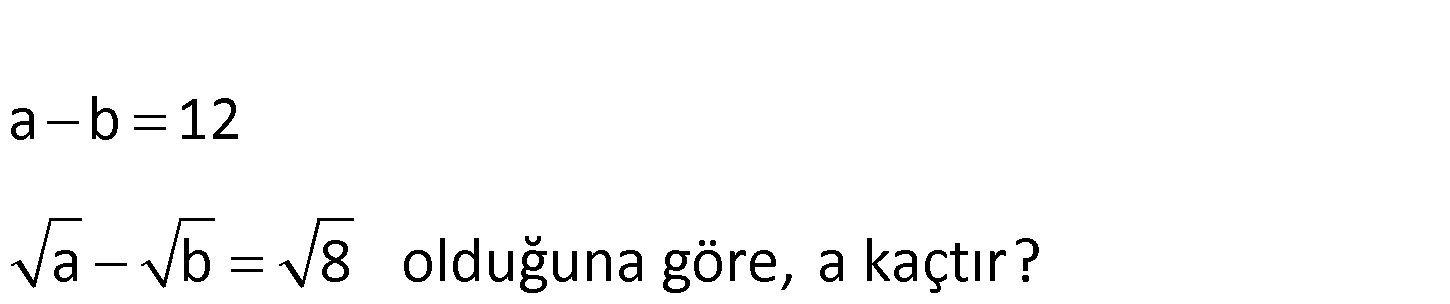

2.SORU


3.SORU
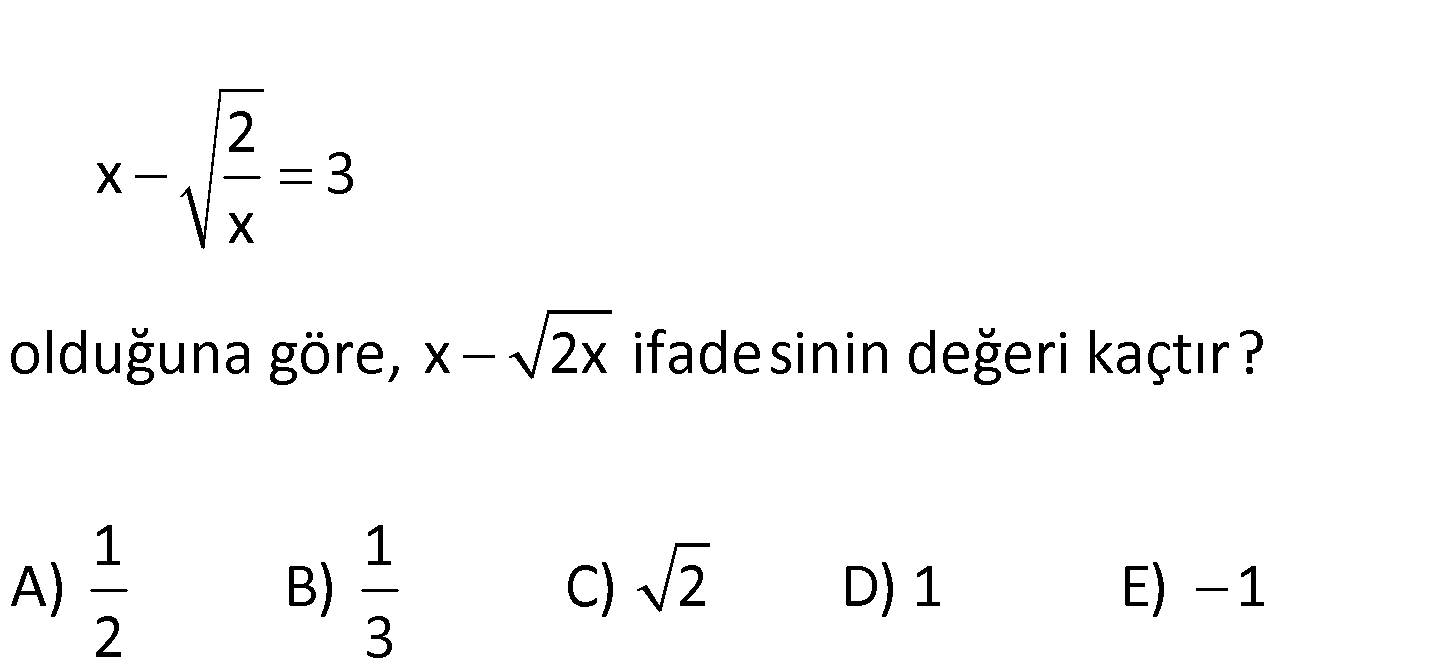
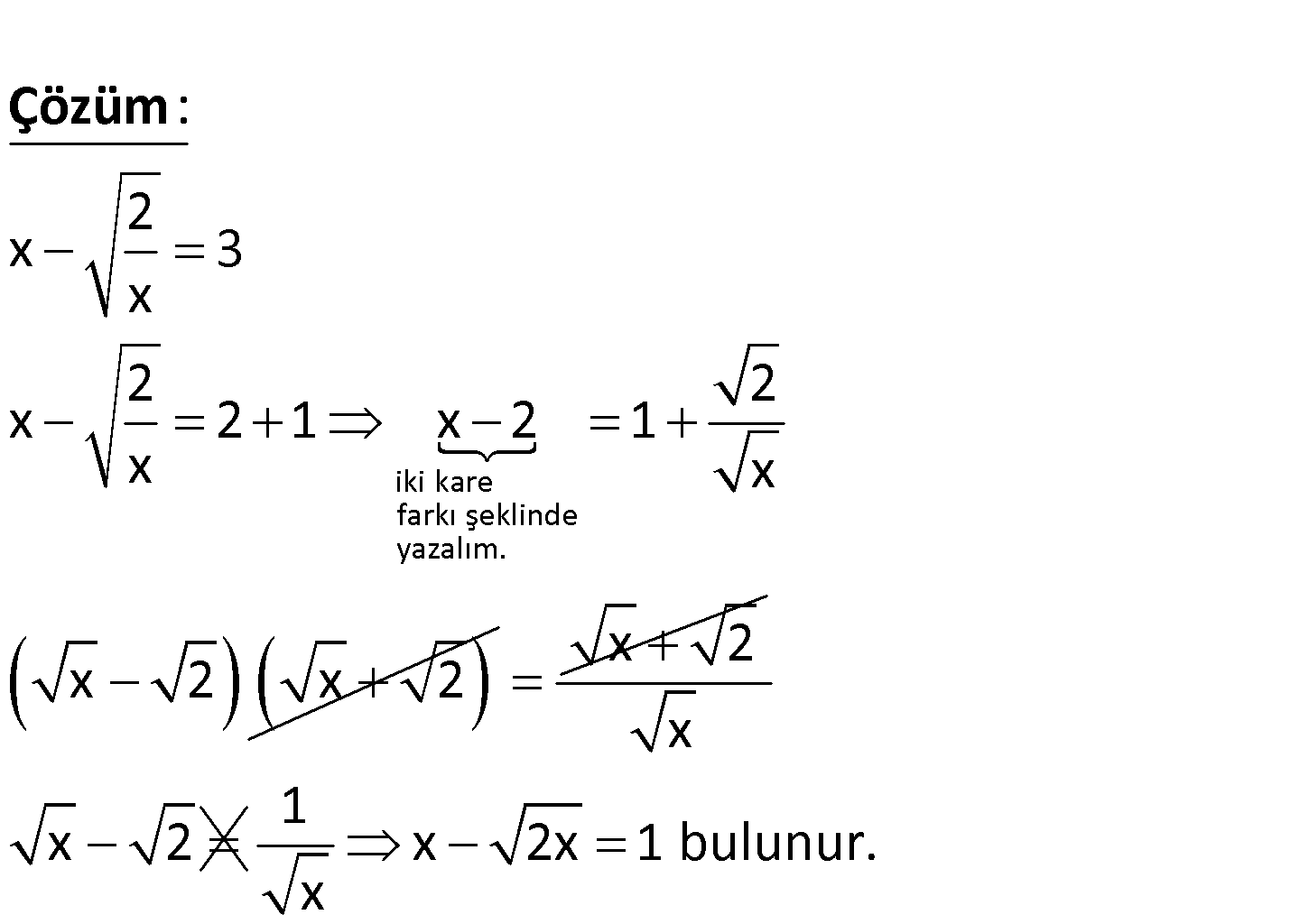
4.SORU
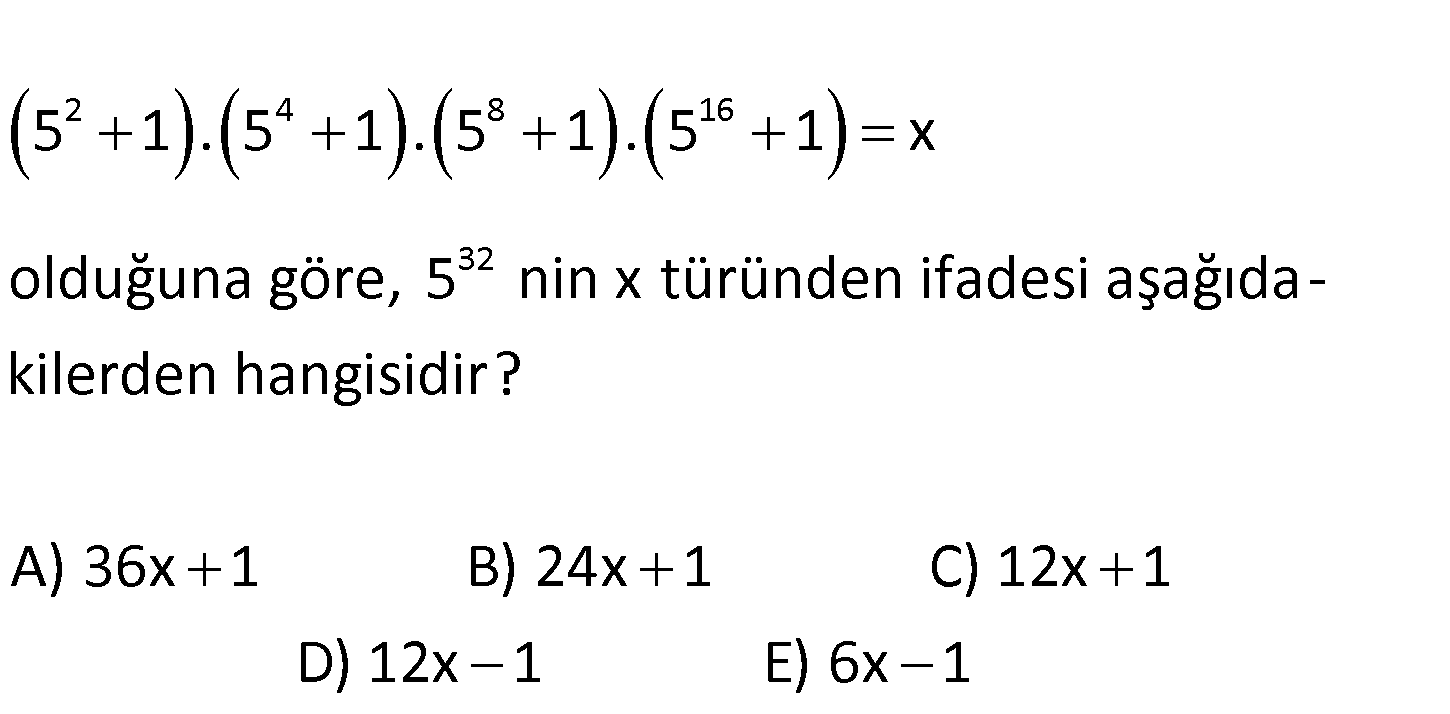
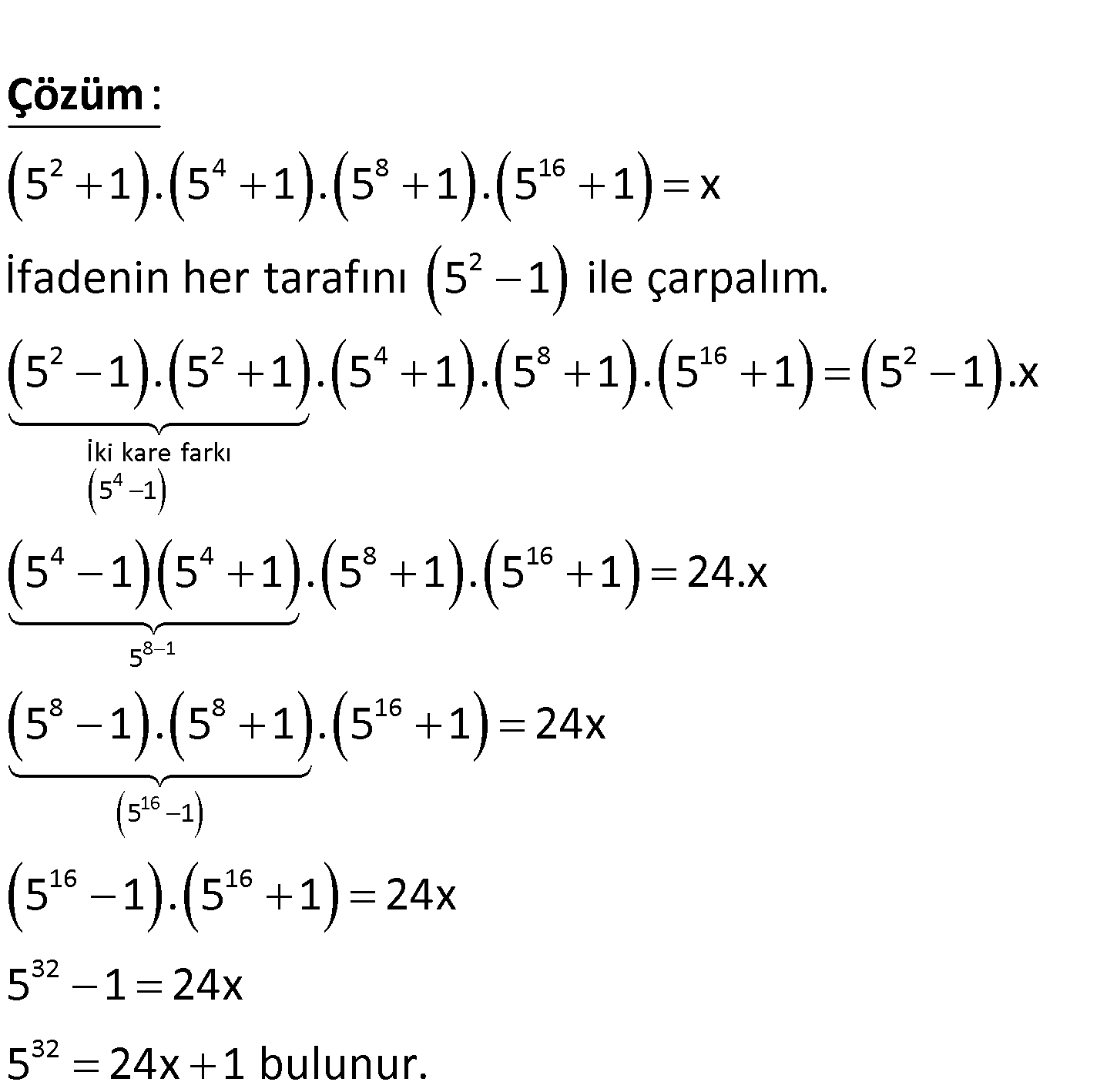
5.SORU
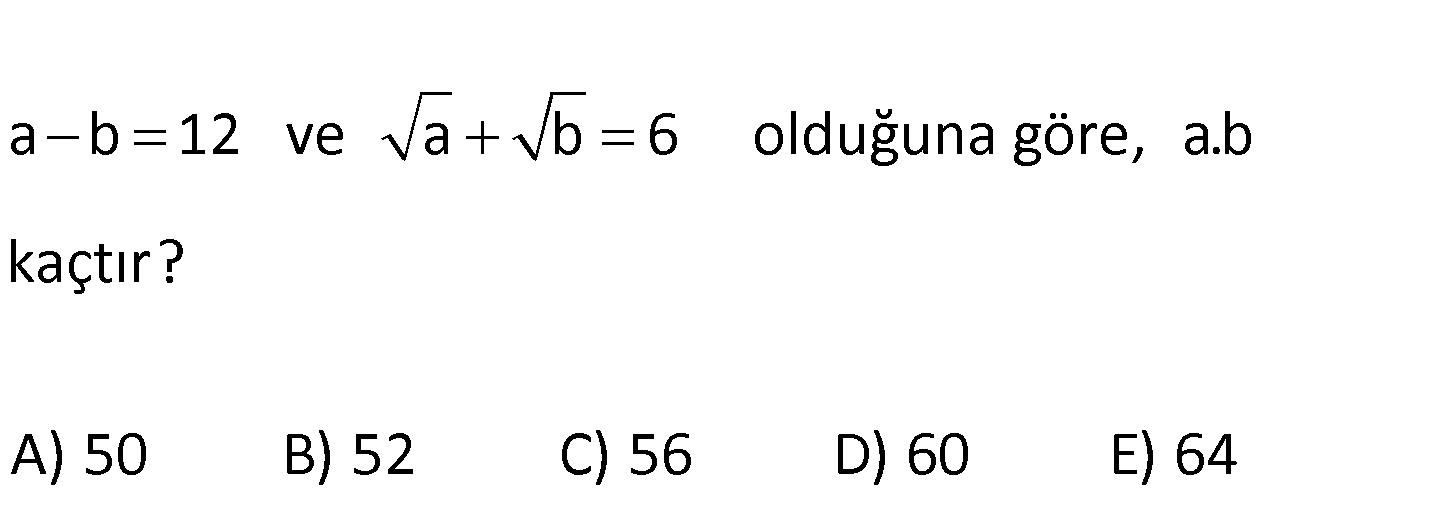
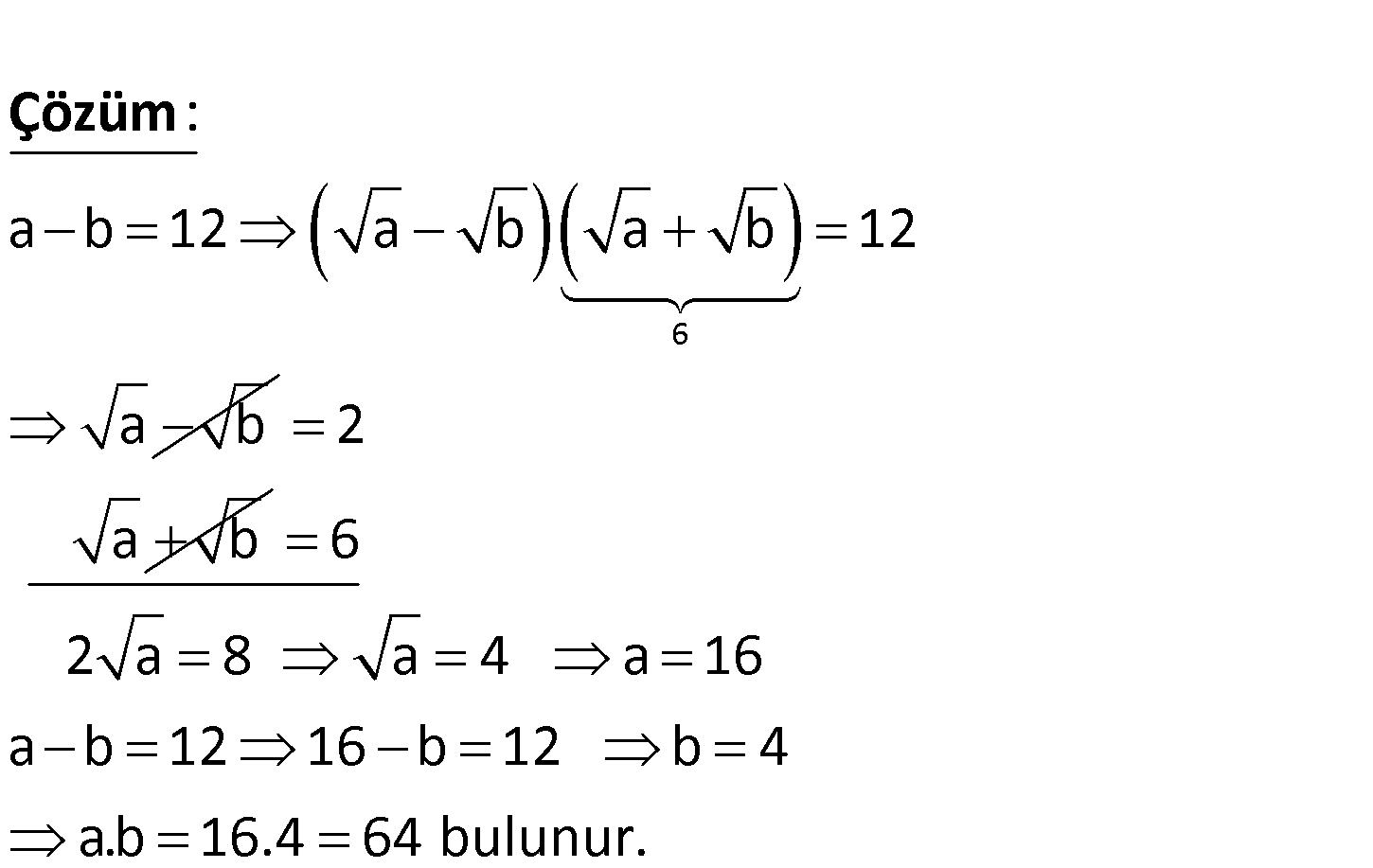
6.SORU

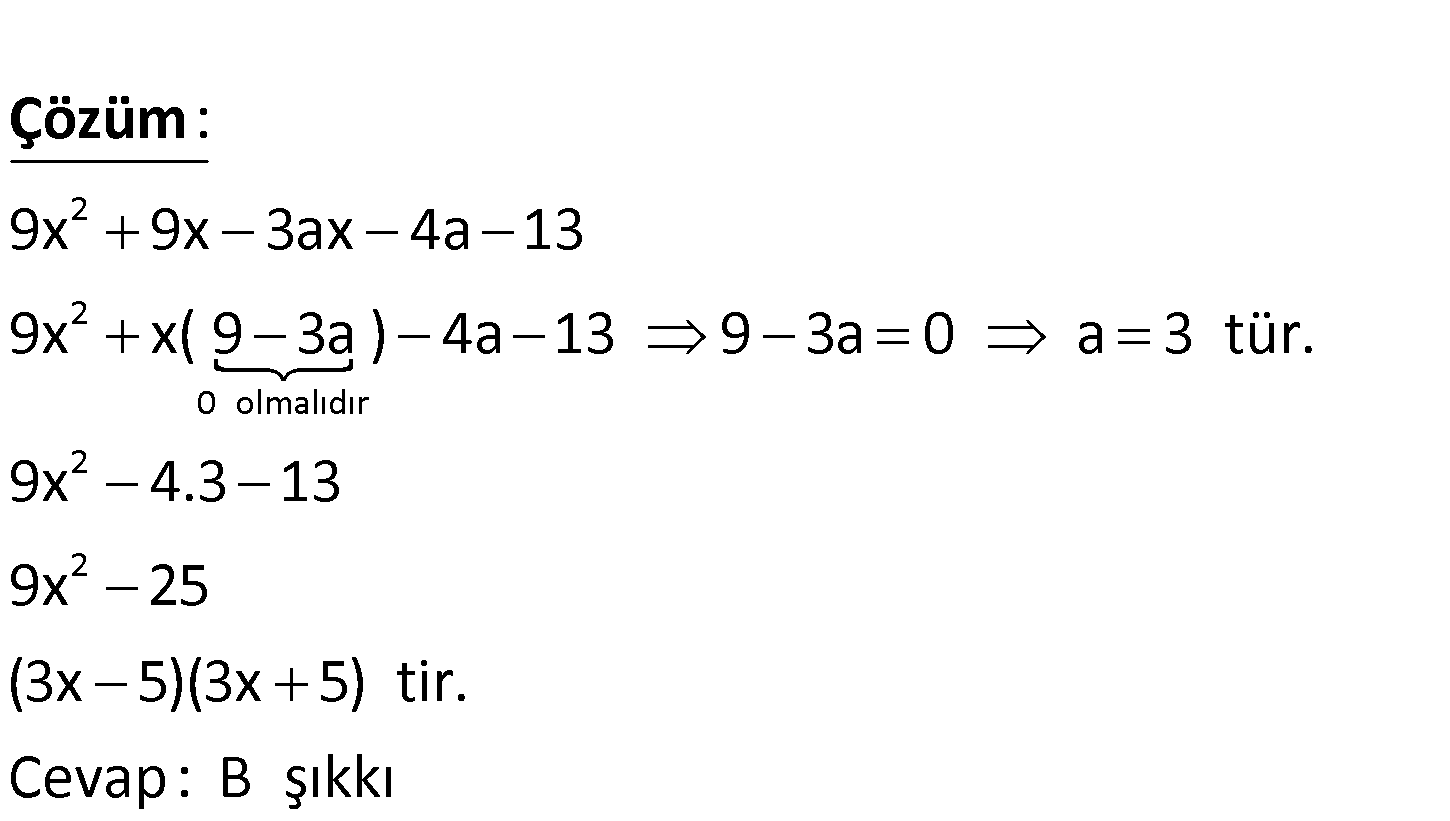
7.SORU
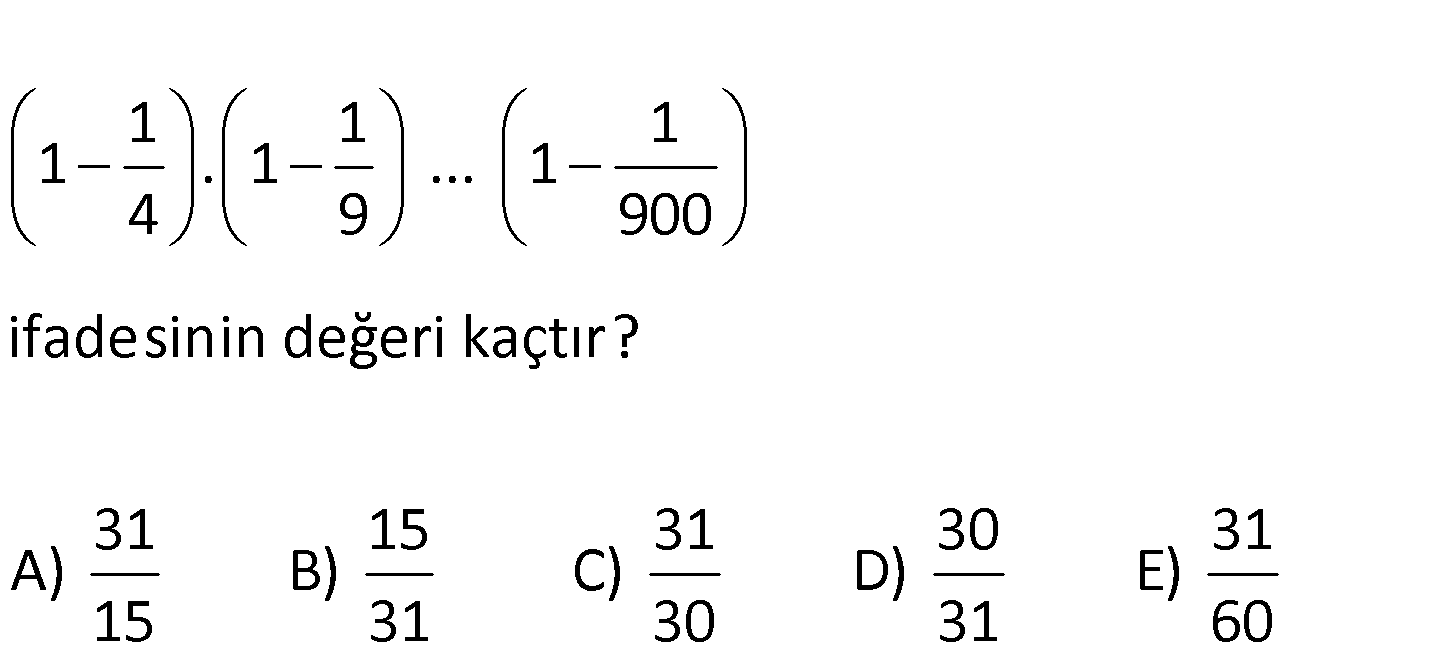
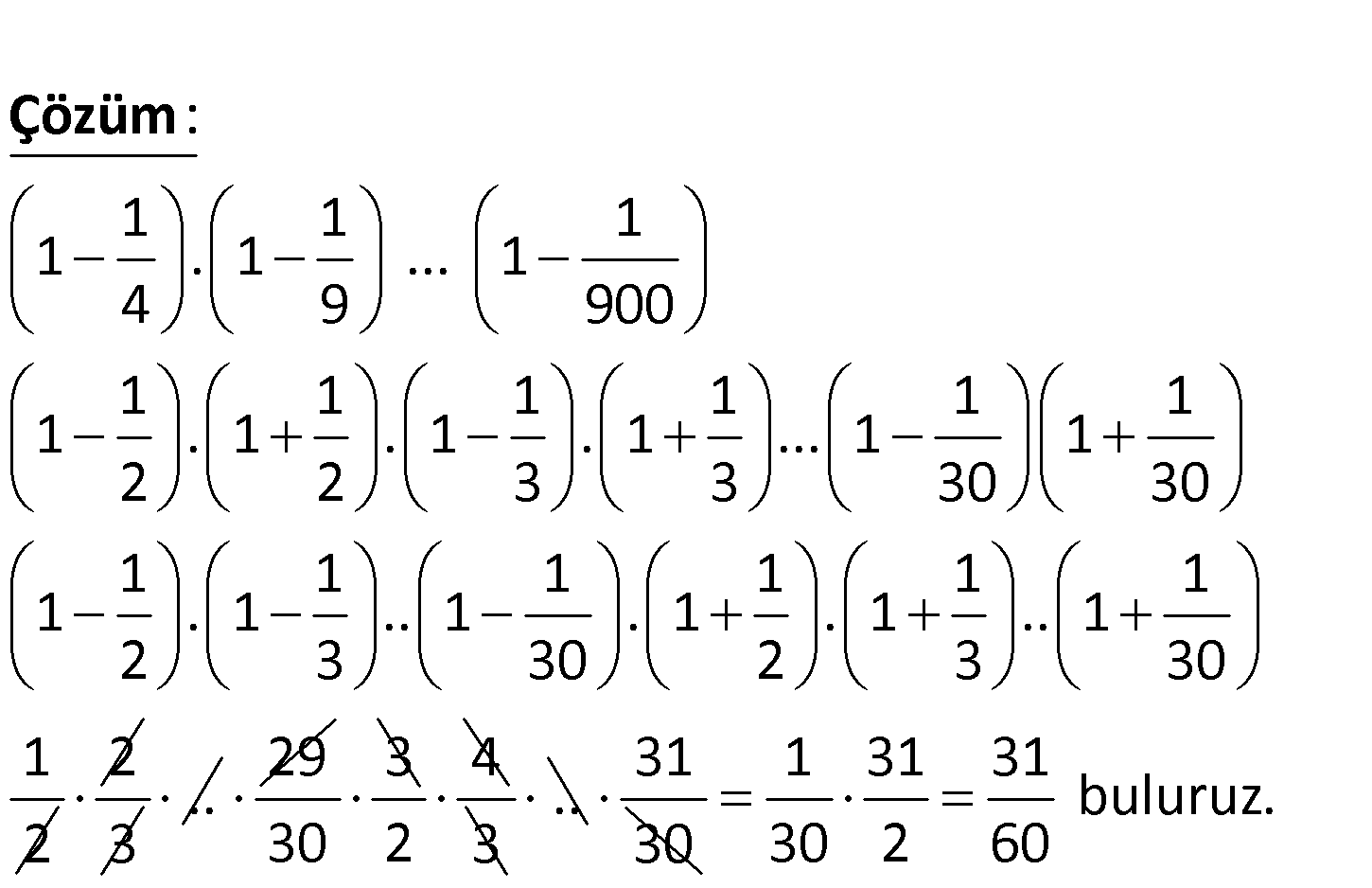
8.SORU

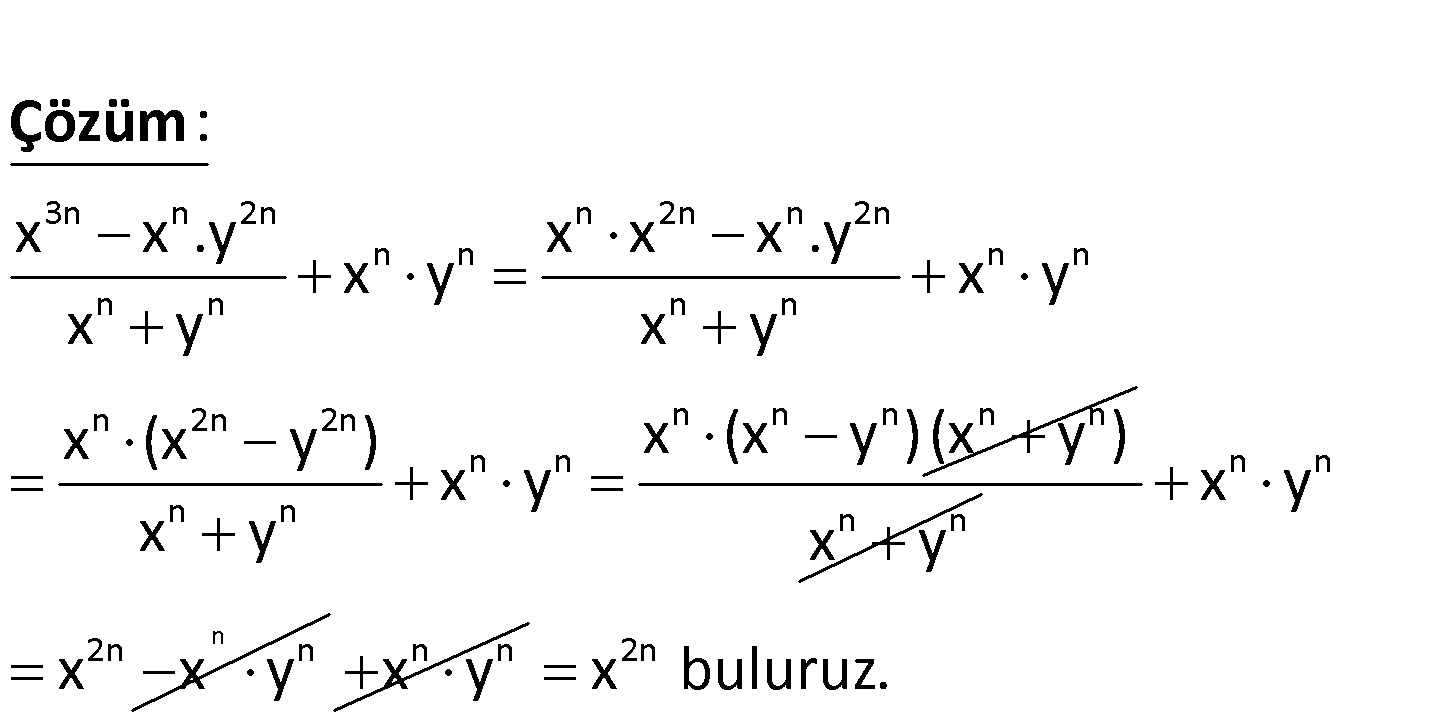
9.SORU


10.SORU

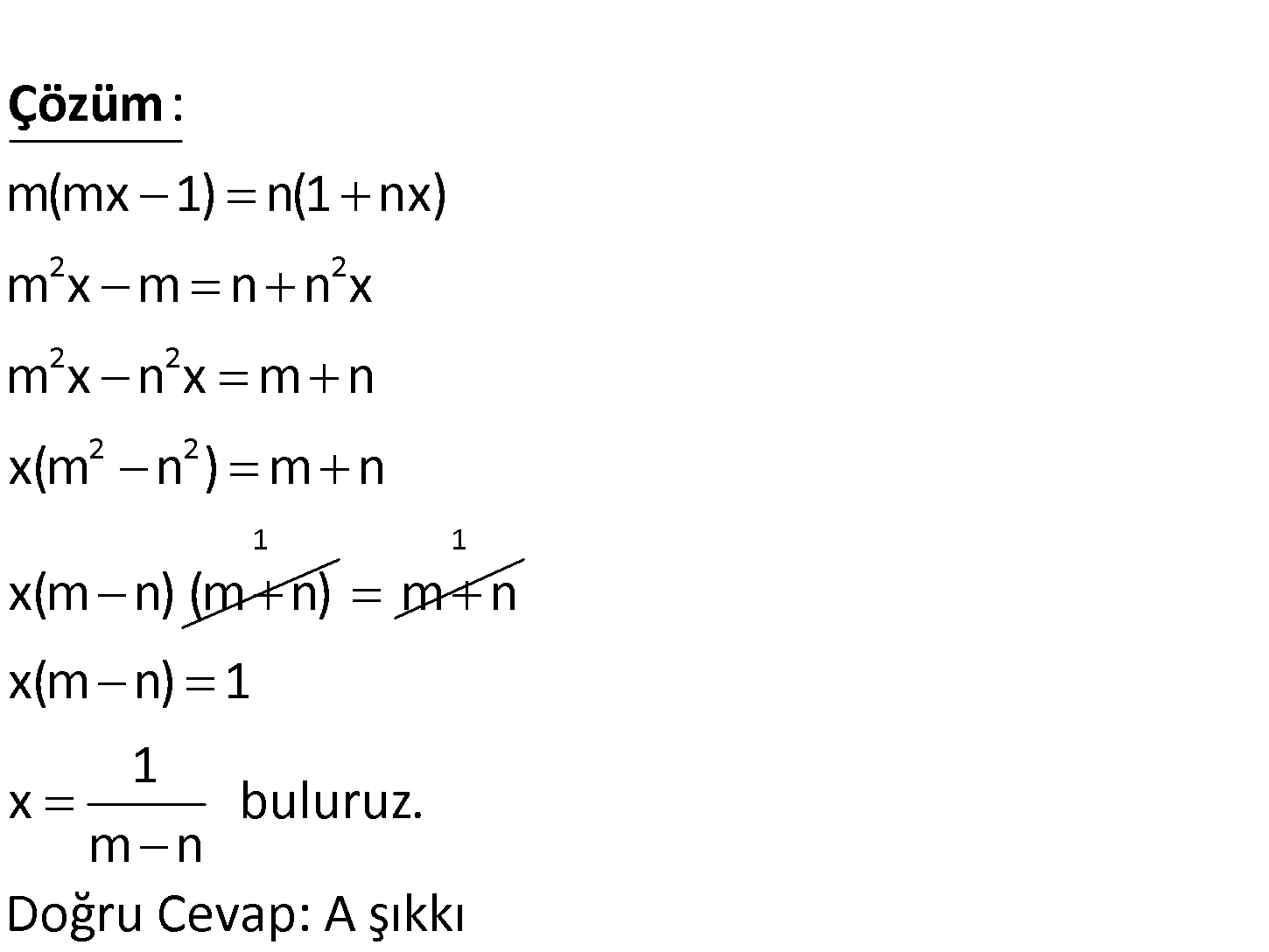
11.SORU


12.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
a b 12 a b 8 olduğuna göre, a kaçtır? 2 2 8 a b 12 ( a) ( b) 12 (İki kare farkı) ( a b).( a b) 12 2 2 ( a b) 12 12 a b : Çözüm 6 2 -2 6 6 2 3 2 dir. 2 2 2 a b 2 2 a b 3 2 taraf tarafa toplarsak; 5 2 2 a 5 2 a 2 25.2 25 a buluruz. 4 2 www.matematikkolay.net 84
x y 12 x y 2 olduğuna göre, x y toplamı kaçtır? A) 18 B) 20 C) 24 D) 26 E) 30 www.matematikkolay.net 2 2 2 2 x x ve y y dir. O halde; x y 12 eşitliğini x y 12 şeklinde yazıp iki : kare farkın Çözüm 2 2 2 4 ı kullanabiliriz. a b (a b)(a b) x y x y 12 x y 6 olmalıdır. x y 2 idi. Taraf tarafa toplarsak; 2 x 8 x 4 x 16 dır. x y 6 16 y 6 y 2 y 4 Buna göre; x y 16 4 20 buluruz. 126
2 x 3 x olduğuna göre, x 2x ifadesinin değeri kaçtır? 1 1 A) B) C) 2 D) 1 E) 1 2 3 iki kare farkı şeklinde yazalım. 2 x 3 x 2 : 2 x 2 1 x 2 1 x x x 2 x 2 Çözüm x 2 x x 2 1 x 2x 1 bulunur. x www.matematikkolay.net 140
2 4 8 16 32 5 1 . 5 1 . 5 1 . 5 1 x olduğuna göre, 5 nin x türünden ifadesi aşağıda – kilerden hangisidir? A) 36x 1 B) 24x 1 C) 12x 1 D) 12x 1 E) 6x 1 www.matematikkolay.net 4 2 4 8 16 2 2 2 İki kare farkı 5 1 5 1 . 5 1 . 5 1 . 5 1 x İfadenin her tarafını 5 1 ile çarpalım. 5 1 . 5 1 : Çözüm 8 1 16 4 8 16 2 4 4 8 16 5 8 8 16 5 1 16 16 32 32 . 5 1 . 5 1 . 5 1 5 1 .x 5 1 5 1 . 5 1 . 5 1 24.x 5 1 . 5 1 . 5 1 24x 5 1 . 5 1 24x 5 1 24x 5 24x 1 bulunur. 111
a b 12 ve a b 6 olduğuna göre, a.b kaçtır? A) 50 B) 52 C) 56 D) 60 E) 64 www.matematikkolay.net 6 a b 12 a b a b 12 a b : Çözüm 2 a b 6 2 a 8 a 4 a 16 a b 12 16 b 12 b 4 a.b 16.4 64 bulunur. 72
2 ifadesi x e bağlı rasyonel katsayılı iki kare farkı şek 9x 9 – linde x 3ax yazılabildiği 4a 1 n 3 e göre, bu ifadenin çarpanların – dan biri aşağıdakilerden hangisidir? A) 3x 2 B) 3x 5 C) 3x 3 D) 9x 1 E) 9x 5 www.matematikkolay.net 2 2 0 olmalıdır 2 2 9x 9x 3ax 4a 13 9x x( 9 3a ) 4a 13 9 3a 0 a 3 tür. 9x 4.3 13 9x 25 (3x 5)(3x 5 : Çözüm ) tir. Cevap: B şıkkı 43
ifadesinin değeri 1 1 1 1 . 1 … 1 4 9 kaçtır? 31 15 31 30 31 A) B) C) D) E) 15 31 30 900 31 60 1 1 1 1 . 1 … 1 4 9 900 1 1 : 1 1 1 1 . 1 . 1 . 1 … 1 2 2 3 3 30 Çözüm 1 1 30 1 1 1 1 1 1 1 . 1 .. 1 . 1 . 1 .. 1 2 3 30 2 3 30 1 2 2 3 .. 29 3 30 4 2 3 .. 31 30 1 31 31 buluruz. 30 2 60 42
3n n 2n n n n n n 2n x x .y x .y x y ifadesinin sadeleşmiş biçimi aşağıdakilerden hangisidir? A) x B) x C n 2n n ) y D) y E) x.y 3n n 2n n 2n n 2n n n n n n n n n n 2n 2n n n n n n n n n n x x .y x x x .y x y x y x y x y x (x y ) x (x y ) (x y ) x x : y y Çözüm n n x y n n n 2n n x y x x y n n x y 2n x buluruz. 15
4 2 4 2 a ve b, 1 den büyük gerçek sayılar olmak üzere, a a b b a.b 8 olduğuna göre, a b toplamının pozitif değeri kaçtır? A) 2 2 B) 3 2 C) 4 2 D) 5 2 E) 6 2 4 2 4 2 4 4 2 2 2 2 2 2 2 2 2 2 a a b b a b a b (a b )(a b ) a b Burada iki çözüm var : 1. cisi (a ) : b Çözüm (a2 b2) a2 b2 2 2 2 2 2 2 a b 1 (Ancak a ve b 1’den büyük olduğu için bu çözüm mümkün değil) 2.cisi a b 0 a b a b dir. a.b 8 ise a.a 8 a 8 a 2 2 dir. a b a a 2a 2.2 2 4 2 buluruz . 2
m ve n reel sayıları için m n olduğuna göre, m mx 1 n 1 nx denklemini sağlayan x değeri a şağıdakilerden han – gisidir? 1 1 1 A) B) C) m n m n m 1 m D) E) n n www.matematikkolay.net 2 2 2 2 2 2 m(mx 1) n(1 nx) m x m n n x m x n x m n x(m n ) m n x(m n) ( : m n) Çözüm 1 mn 1 x(m n) 1 1 x buluruz. m n Doğru Cevap: A şıkkı 5
2 2 2 2 2 2 a c 6 8 b olmak üzere, a c b 2ab a c b 2ac ifadesinin a cinsinden eşiti aşağıdakilerden hangi si – dir. a 1 a 2 a 1 A) B) C) a 1 a 1 a 2 a 2 a 2 D) E) a 2 a 2 www.matematikkolay.net 2 2 (a b) 2 2 2 2 2 2 2 2 2 2 2 2 (a c) 2 2 a c 6 8 b a c b 2ab a 2ab b c a c b 2ac a 2ac c b (a b) c (a : Çözüm 2 2 (a b c). (a b c) c) b (a c b) .(a c b) a b c a (b c) a c b a (b c) c 6 8 b b c 2 a (b c) a 2 bulunur. a (b c) a 2 96
16 3 1 sayısı aşağıdakilerden hangisine tam bölü – nemez? A) 20 B) 32 C) 41 D) 45 E) 80 www.matematikkolay.net 16 8 8 4 4 8 2 2 4 8 2 4 8 3 1 (3 1)(3 1) (3 1)(3 1)(3 1) (3 1)(3 1)(3 1)(3 1) (3 1)(3 1)(3 1)(3 1)( : 3 1) Çözüm 8 2 8 5 8 5 8 5 2.4.10.82.(3 1) 2.2 .2.5.41.2.(3 1) 2 .5.41.(3 1) tir. Şıklarda verilen sayıları asal çarpanlara ayırarak, 2 .5.41.(3 1) in içinde bu çarpan var mı, yok mu inceleyelim. 32 2 dir. var, 32’ye tam 2 4 2 bölünür. 20 2 .5 dir. var, 20’ye tam bölünür. 41 var, 41’e tam bölünür. 80 16.5 2 .5 var, 80’e tam bölünür. 45 3 .5 3 çarpanı yok, Tam bölünemez. 100


Teşekkür ederim.Konuyu yeni öğrenenler için zorlayıcı bir testti bence iyice hakim olduysanız çözmeyi denemenizi öneririm.