Soru Sor sayfası kullanılarak Bölme konusu altında Bölme işlemi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

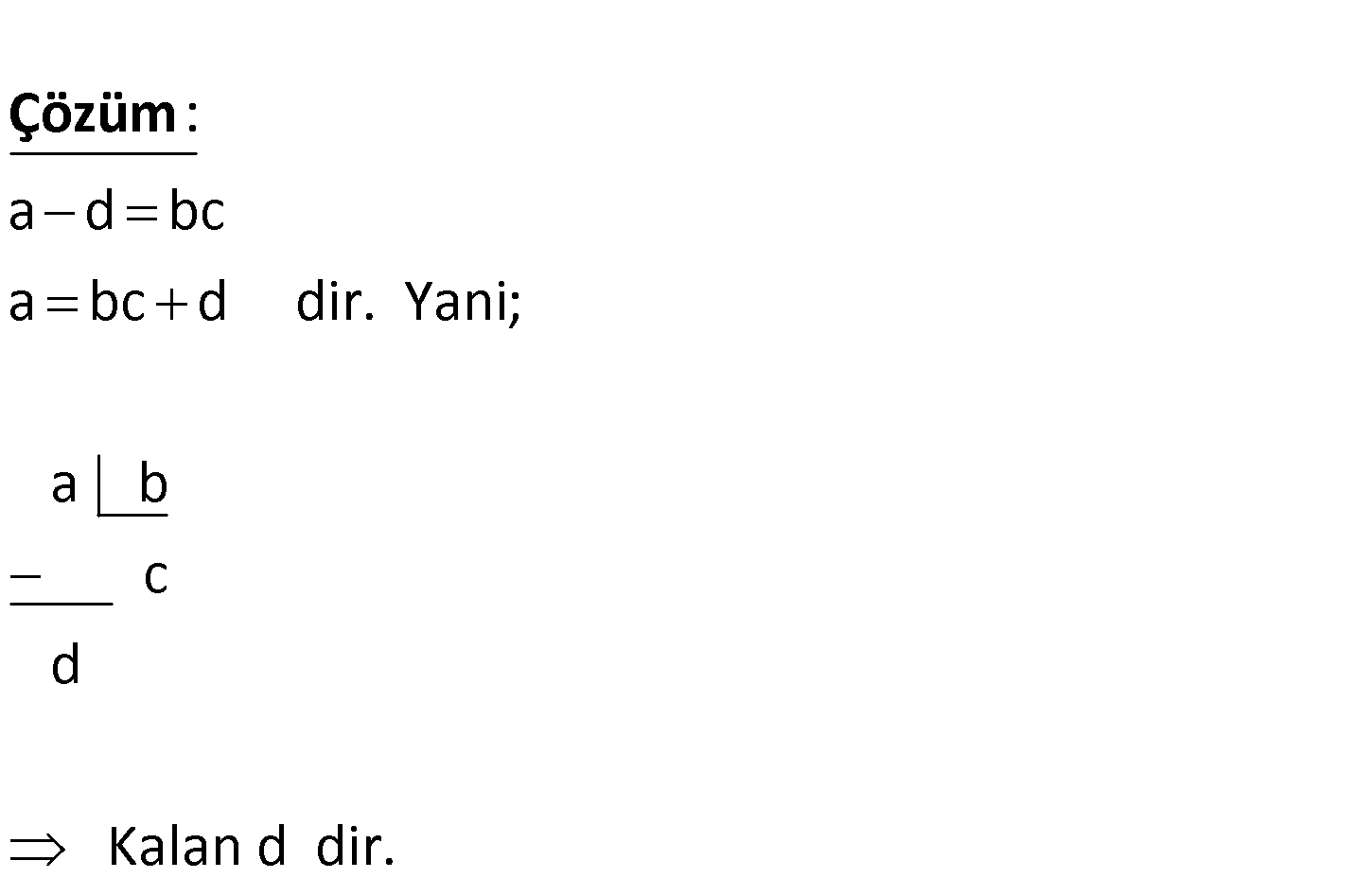
3.SORU


4.SORU
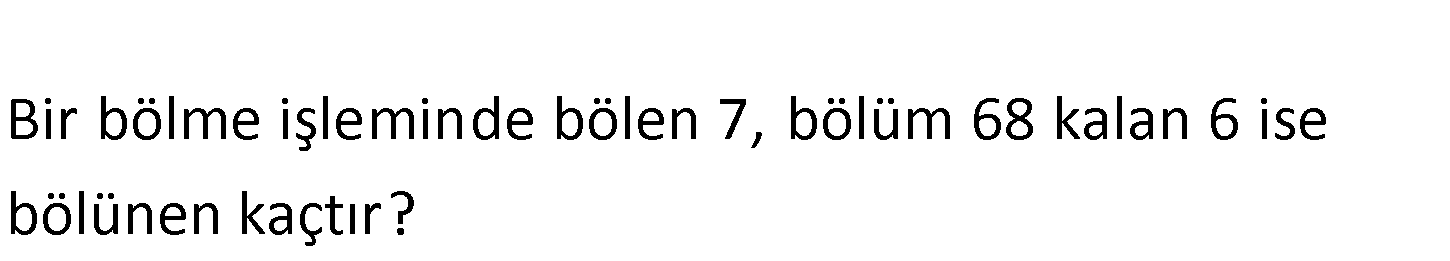
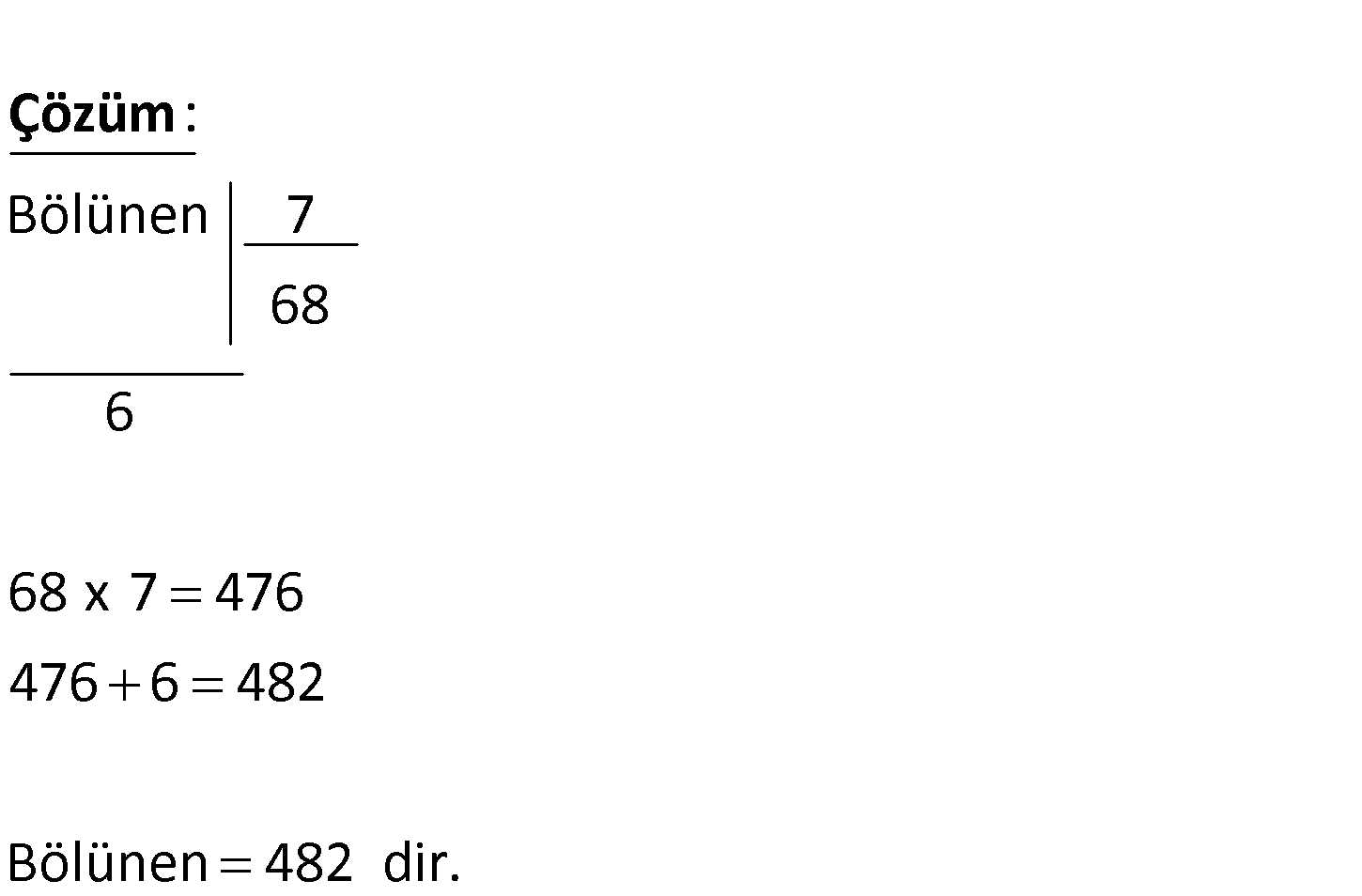
5.SORU


6.SORU


7.SORU


8.SORU

9.SORU


10.SORU


11.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net 51515 51 bölüm ile kalanın toplamı? _ x y Bölme işlemini gerçekleştirelim, 51515 51 51 1010 51 51 5 Bölüm: 10 : 10 Kal Çözüm an: 5 Buna göre; Bölüm+Kalan=1010+5=1015 bulunur. 7
a, b, c, d doğal sayılar, d b ve a d bc ise a’nın b’ ye bölümünden kalan kaçtır? A) c B) d C) 0 D) 1 E) c d a d bc a bc d dir. Yani; a b c d Kalan d dir. : Çözüm www.matematikkolay.net 17
kl ve ml iki basamaklı sayılardır. 999 kl ml 0 k l m toplamı kaçtır? A) 12 B) 10 C) 8 D) 6 E) 5 999 9.111 9.37.3 27.37 dir. kl 37 ml 27 olmalıdır. k l m 3 7 2 12 buluruz. : Çözüm www.matematikkolay.net 25
? Bir bölme işl eminde bölen 7, bölüm 68 kalan 6 is e b öl ü n e n k a ç tır . Bölünen 7 68 6 : 68 x 7 476 476 6 482 Bölünen 482 dir Çözüm 26
? 30 30 3 0 3 0 3 : 3 3 www.matematikkolay.net 0 303030303 303 303 100010 : 0 303 303 0 Çözüm 3 Bölüm1000100 , Kalan 3 tür. 38
r Üç basamaklı 3ab sayısının 29 ile bölümünden elde edilen bölüm 12 ve kalan 4 olduğuna göre, a.b ça pımı kaçtır? www.matematikkolay.net 3ab 29 _ 12 4 Buna göre; 3 ı : ab 29×12 4 olmalıd r. 3ab 348 4 3ab 352 dir. a Çözüm 5 b 2 olmalıdır. a.b 5.2 10 buluruz. 43
? Bir bölme işleminde bölünen ile bölenin t oplamı 95, bölüm 4 ise bölünenle bölen kaç tır Bölünen 4. Bölen dir. Bölünen Bölen 95 ise 4. Bölen Bölen 95 5. Bölen 95 : Çözüm Bölen 19 dur. Bölünen 4. Bölen 4.19 76 dır. 53
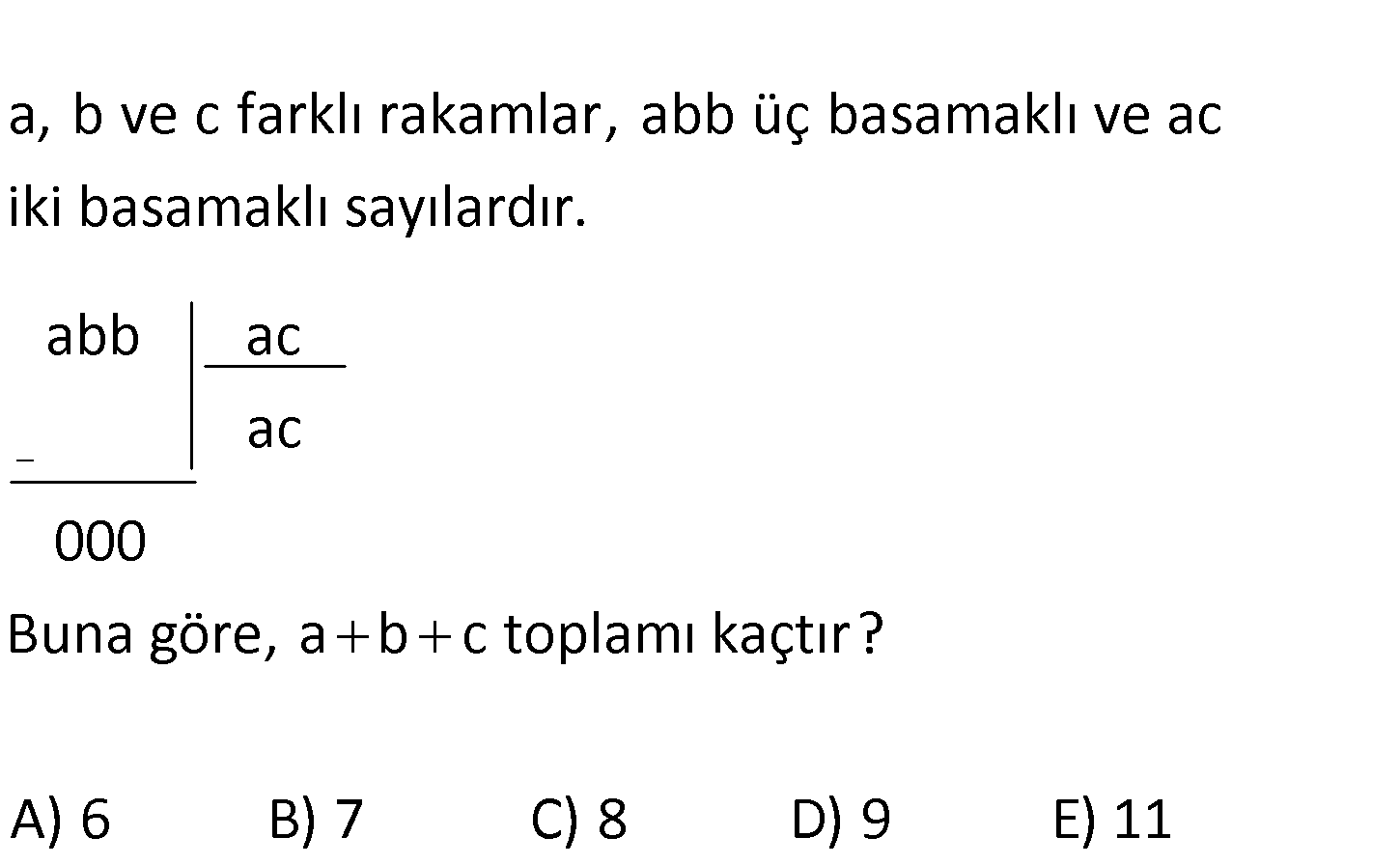
a, b ve c farklı rakamlar, abb üç basamaklı ve ac iki basamaklı sayılardır. abb ac ac 0 Buna göre, a b c toplamı kaçtır? A) 6 B) 7 C) 8 D) 9 E) 11 2 2 abb ac dir. a 1,2 ya da 3 tür. Çünkü 40 1600 4 basamaklıdır. 30’lu sayıların karesi 900 : Çözüm 2 2 den başlar. Yani a 3 olup abb sayısı 9’la başlayamaz. 20’li sayıların karesi 400 den başlar. Yani a 2 olup abb sayısı 4’le başlayamaz. O halde a 1 olmak zorundadır. 1bb 1c ise 100 10b b 10 c 1 00 11b 100 2 4 2 22 20c c 11b c 20 c b 4 ve c 2 olmalıdır. Cevap a b c 1 4 2 7 buluruz. 55
www.matematikkolay.net AB ve BA iki basamaklı doğal sayılardır. AB BA 1 27 Yukarıdaki bölme işlemine göre, A B farkı kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 AB BA 27 dir. Sayıları çözümleyerek yazalım. 10A B 10B A 27 9A 9B 27 9 A B 27 A B 3 bulur : Çözüm uz. 57
www.matematikkolay.net aa ve bc iki basamaklı doğal sayılardır. aa 9 bc a 8 Yukarıdaki bölme işlemine göre, a b c toplamı kaçtır? A) 13 B) 14 C) 15 D) 16 E) 17 aa 9.a 8 dir. aa’yı çözümleyerek yazalım. 10.a a 9.a 8 11.a 9.a 8 2.a 8 a 4 tür. bc 9.a : Çözüm dır. bc 9.4 36 buluruz. b 3 ve c 6 dır. O halde; a b c 4 3 6 13 buluruz. 62
xy iki basamaklı bir sayı ve x y olmak üzere; xy x y Yandaki bölme _ 5 3 2 2 işlemine göre, x y 2.x.y nin değeri kaçtır? A) 27 B) 18 C) 9 D) 3 E) 1 İki basamaklı bir sayı Sonu 5 ya da 0 ile biter xy 5(x y) 3 Sonu 0 ile biterse xy : …0 Çözüm 3 …3 y 3 olur. x3 5(x 3) 3 10x 3 5x 15 3 5x 18 3 5x 15 x 3 tür. x y olmamalıydı. Bu çözümü alamayız. Sonu 5 ile biterse xy …5 3 …8 y 8 olur. x8 5(x 8) 3 10x 8 5x 40 3 5x 43 8 5x 35 x 7 5 2 2 2 2 2 dir. 5.(7 8) 75 olur. 5 ile bitiyor. O halde; x y 2.x.y (x y) (7 8) ( 1) 1 buluruz. www.matematikkolay.net 70

