Soru Sor sayfası kullanılarak Belirsiz İntegral konusu altında Köklü ifadelerin integrali ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
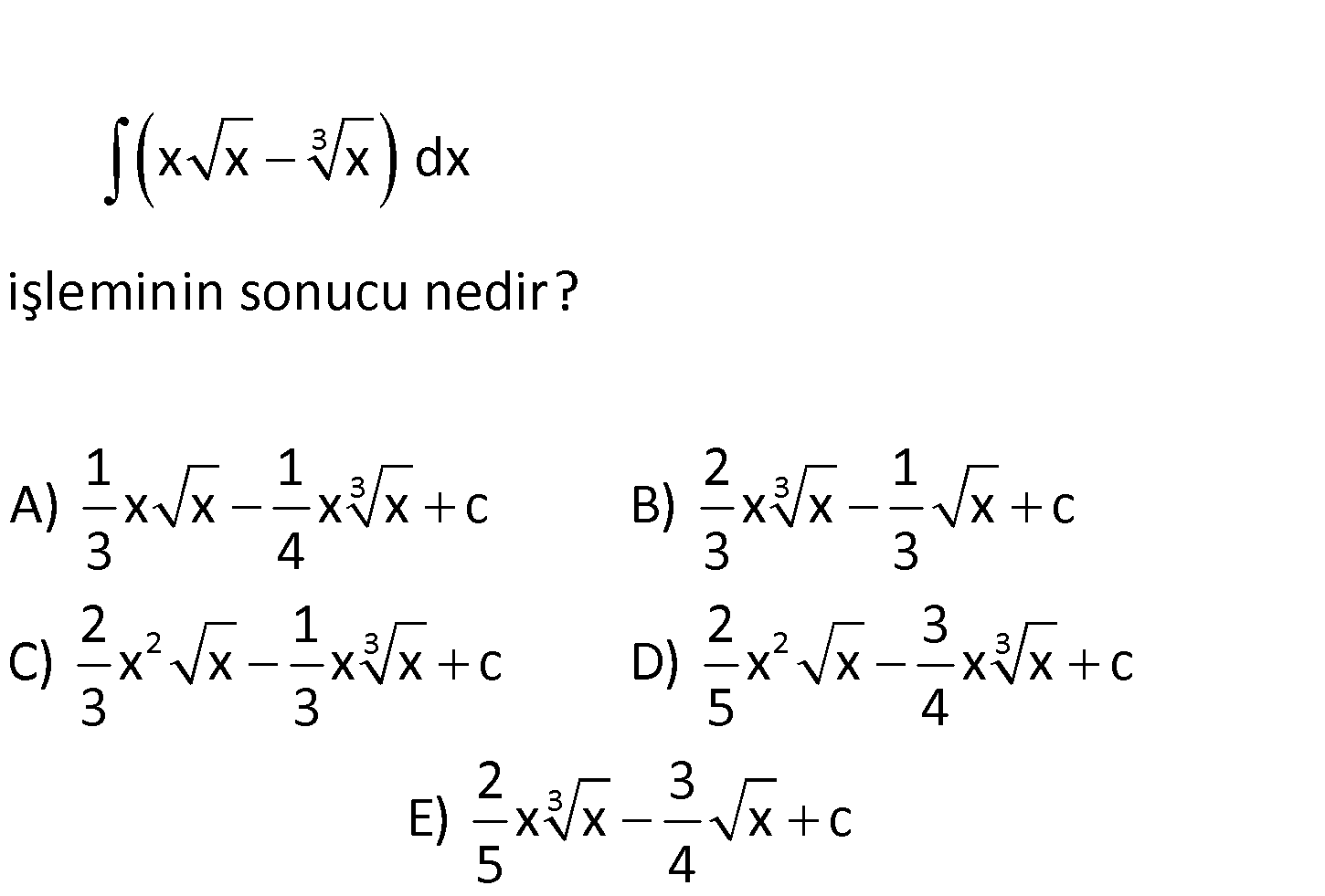
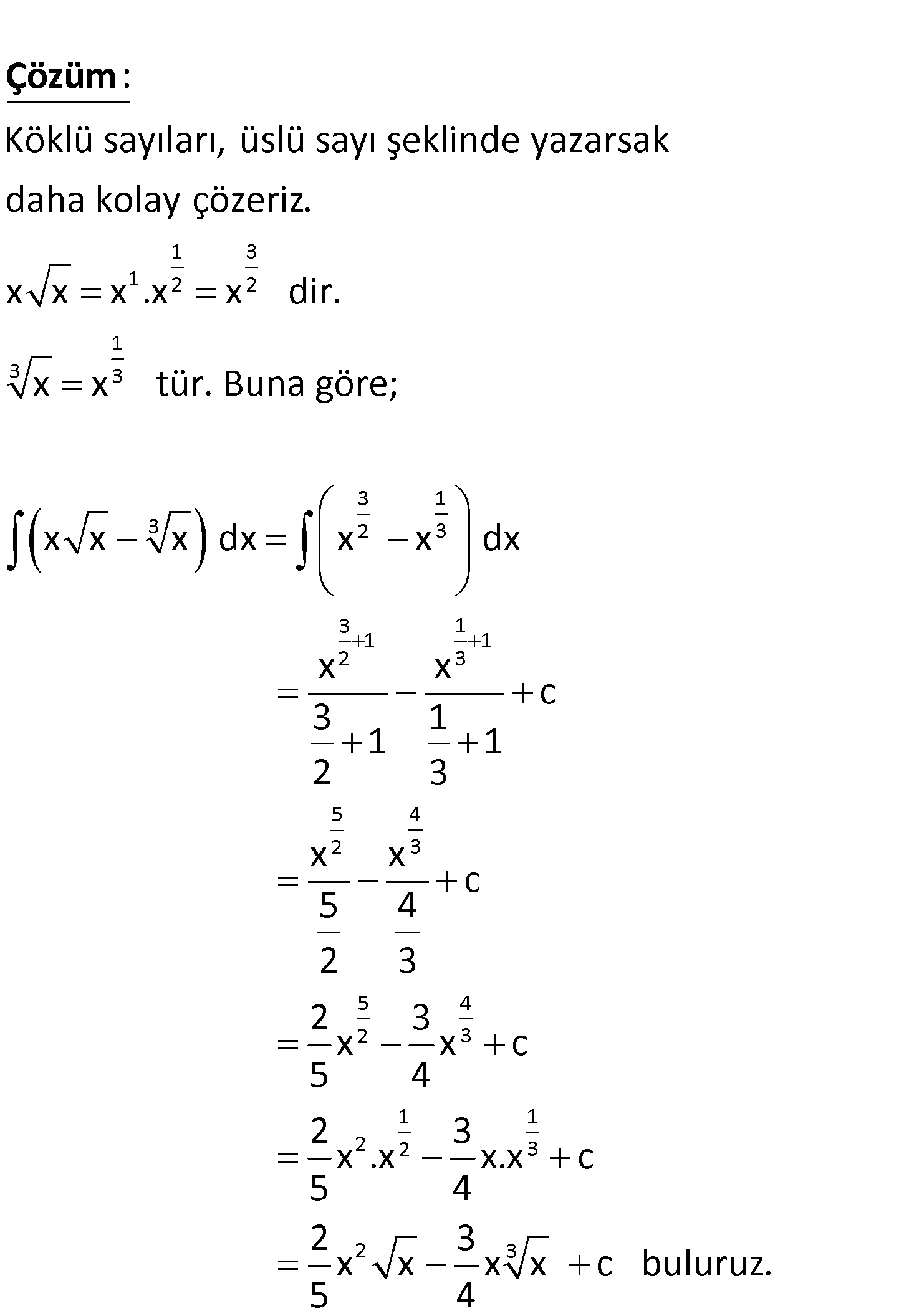
2.SORU
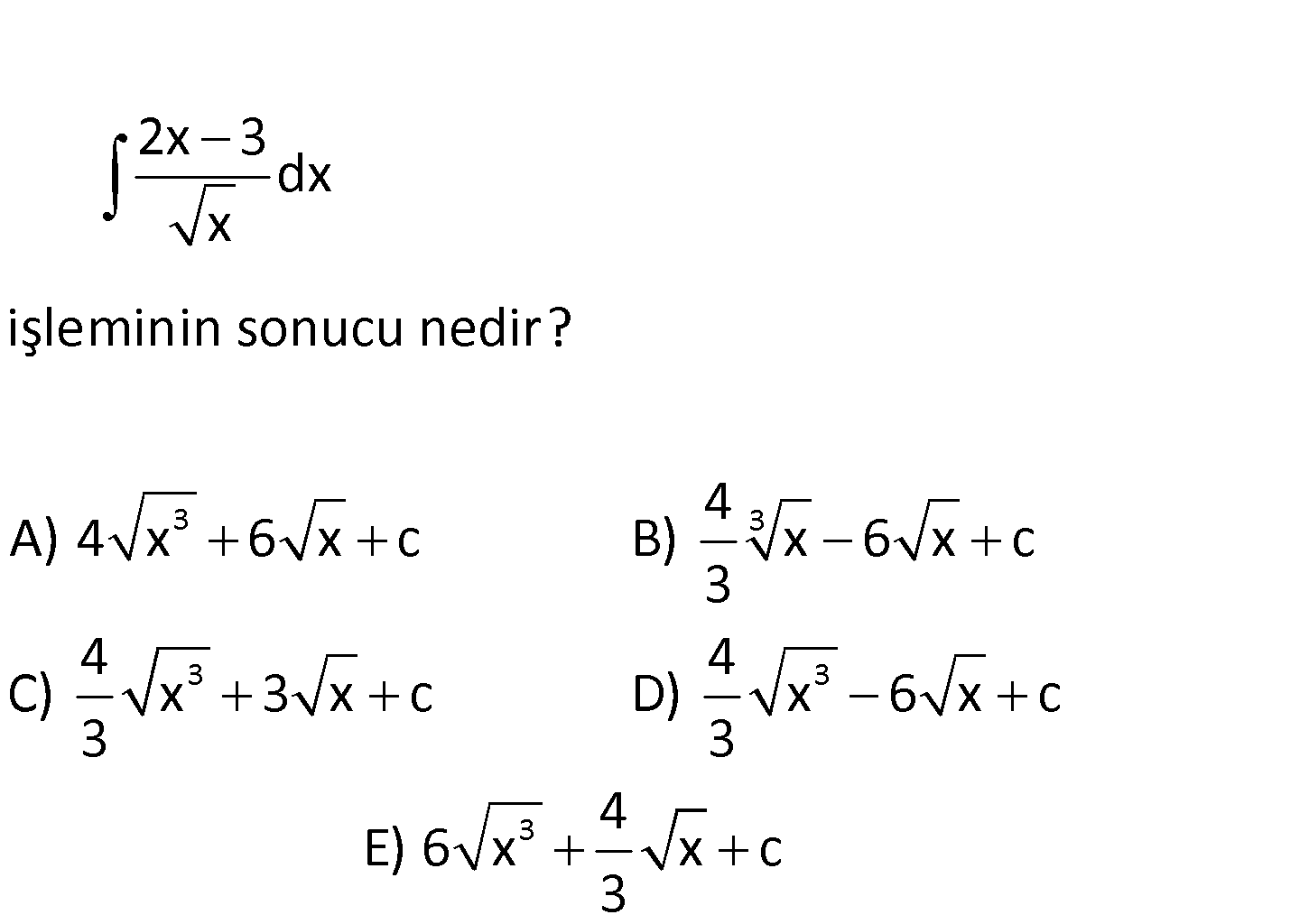
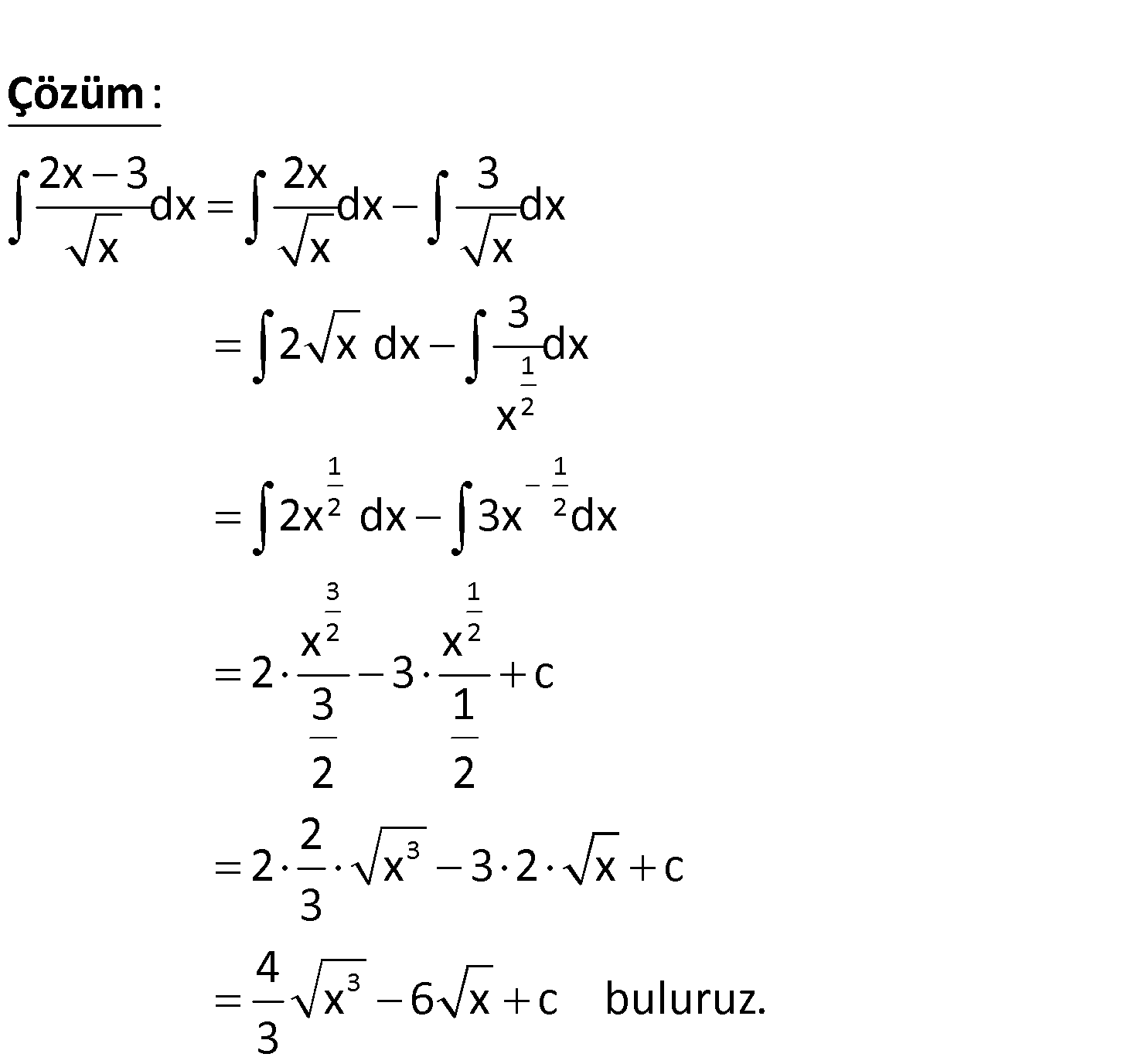
3.SORU

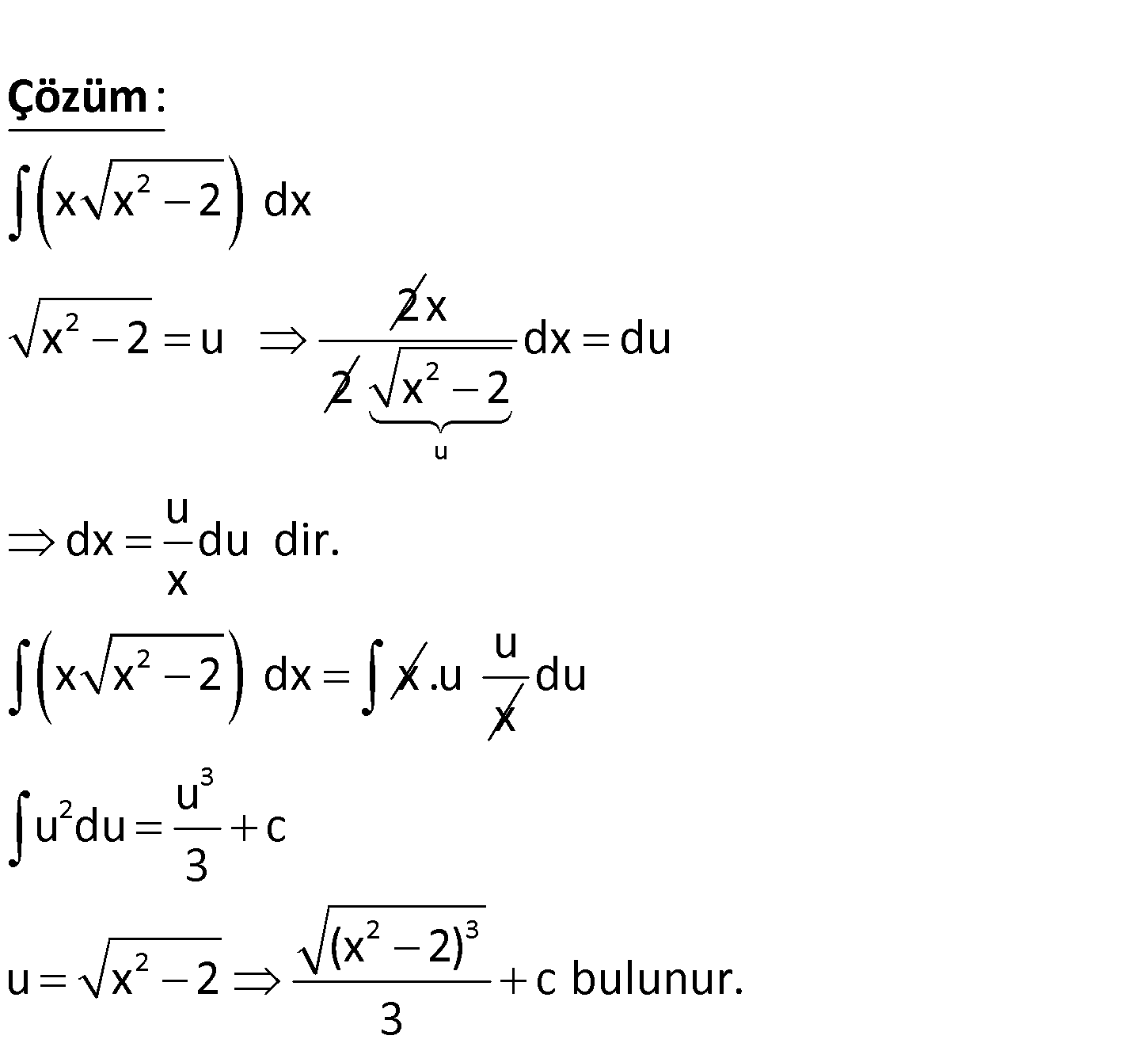
4.SORU
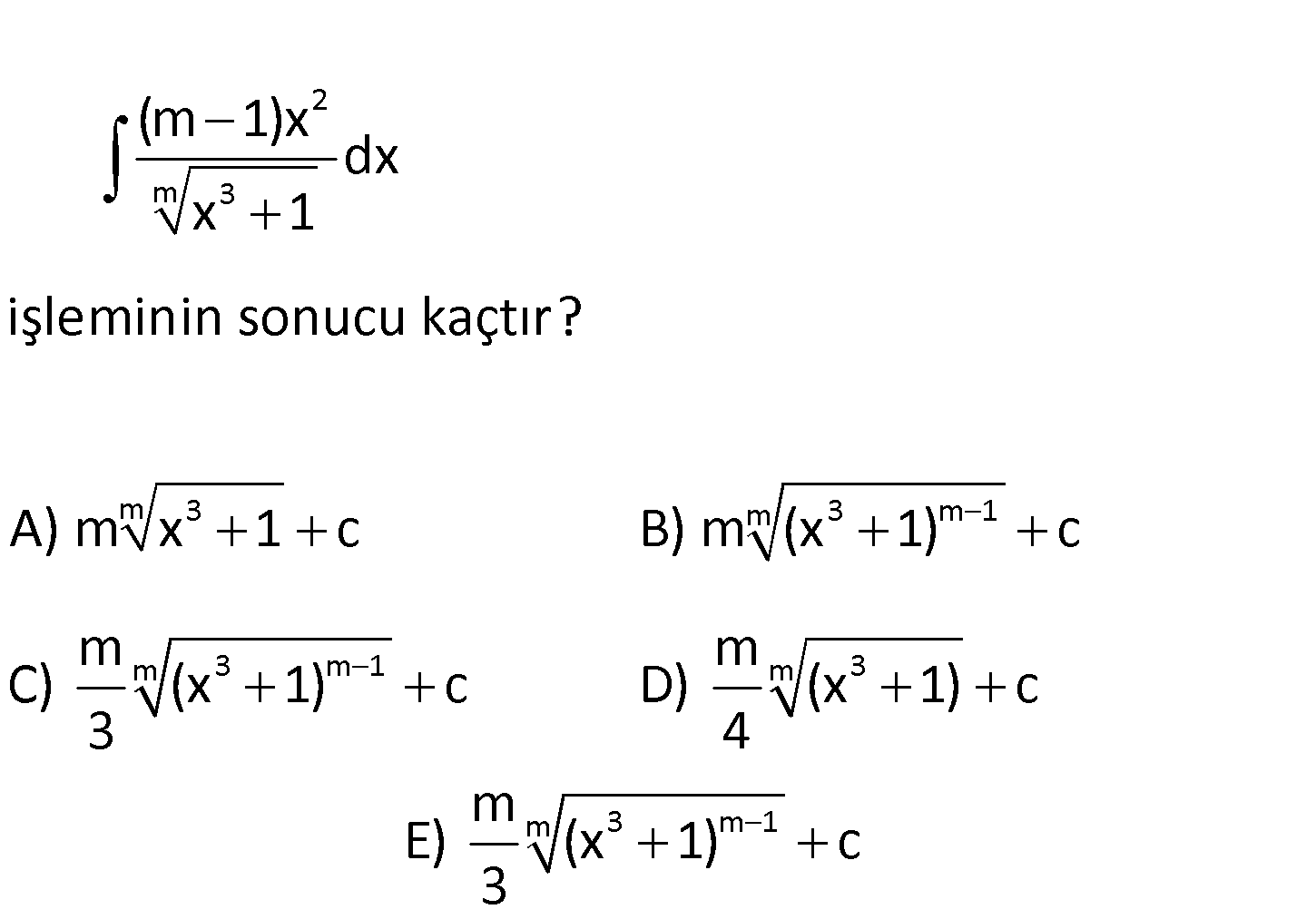
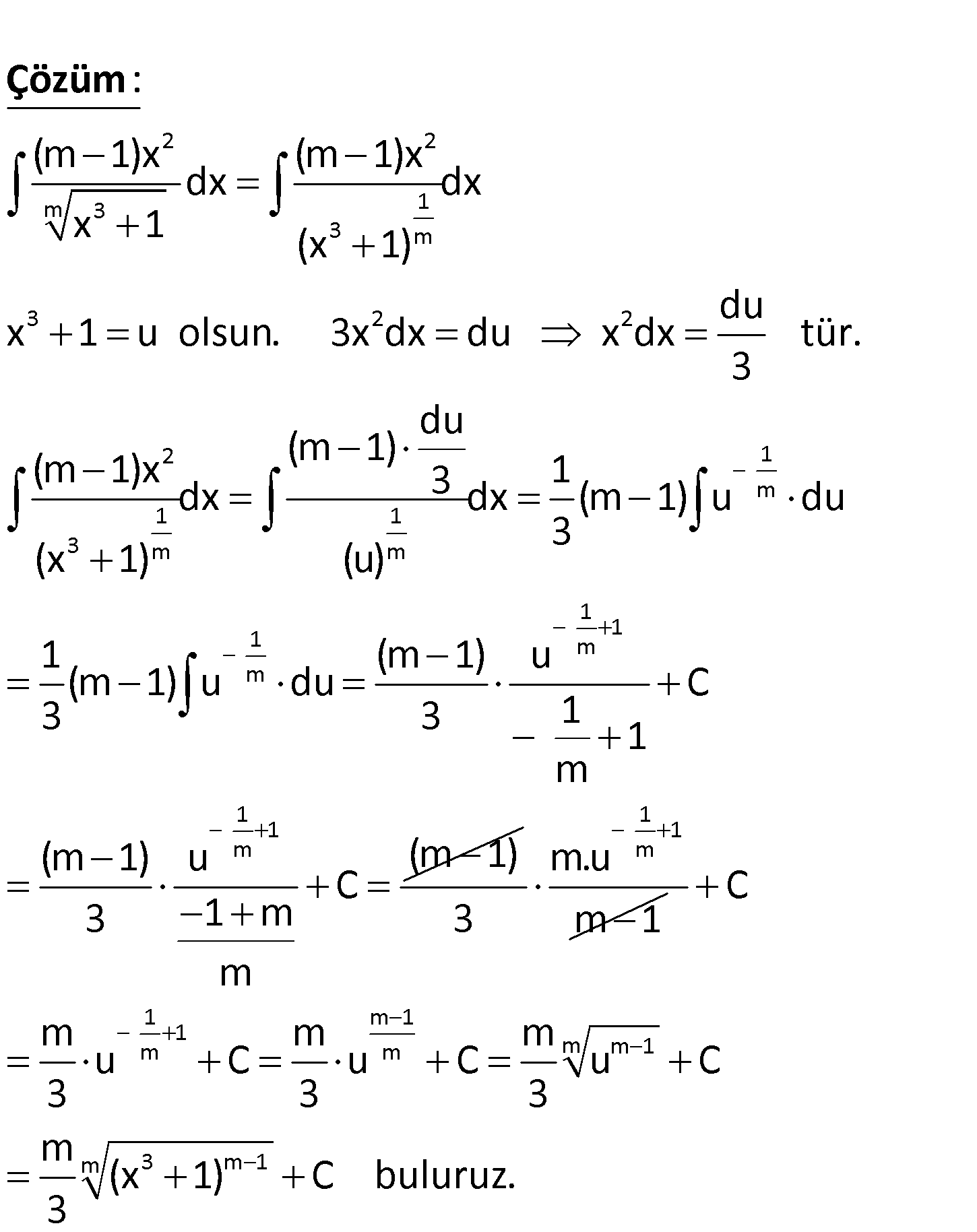
Burdan sonraki sorular, Fen Lisesi Müfredatı için geçerlidir.
5.SORU
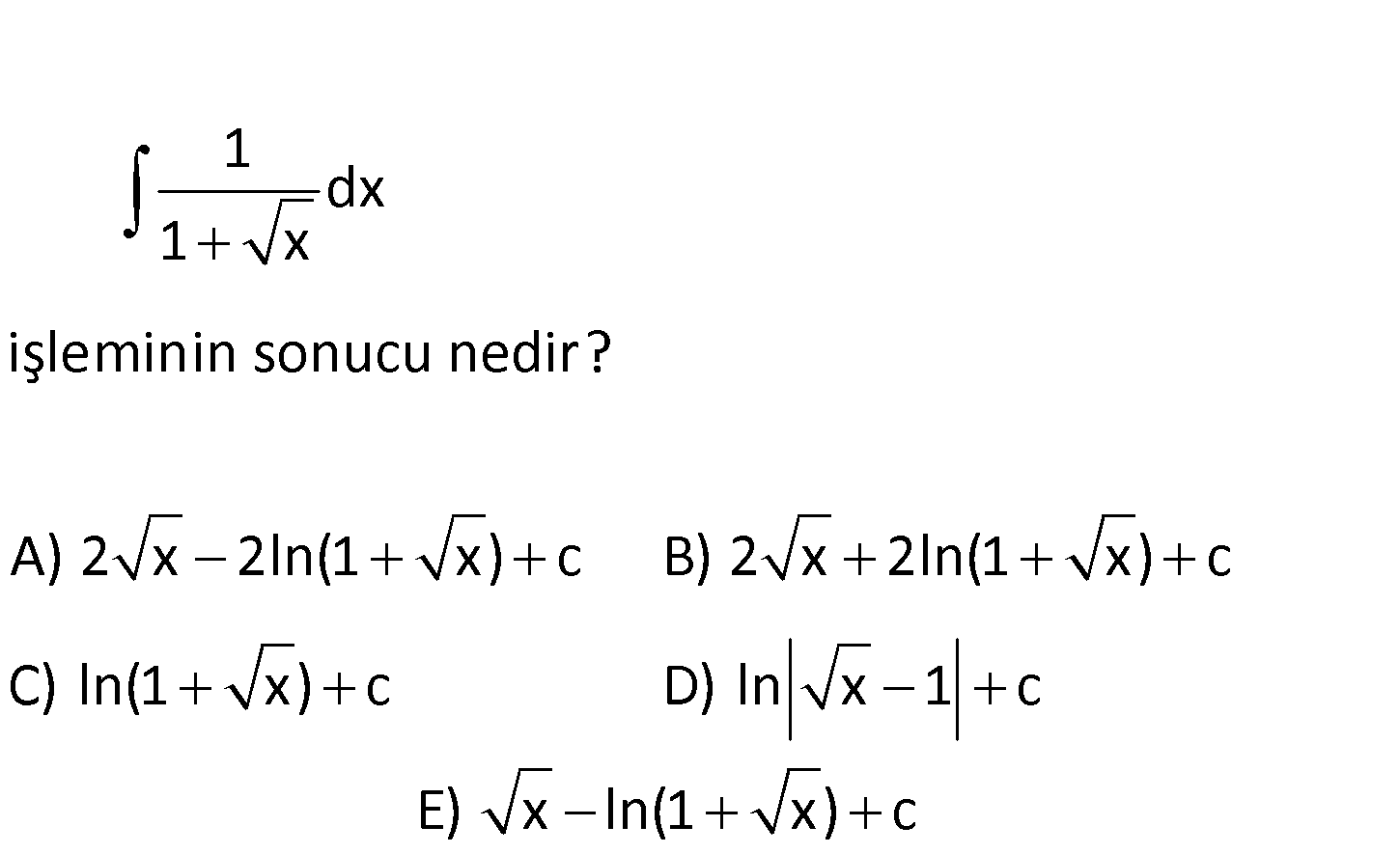
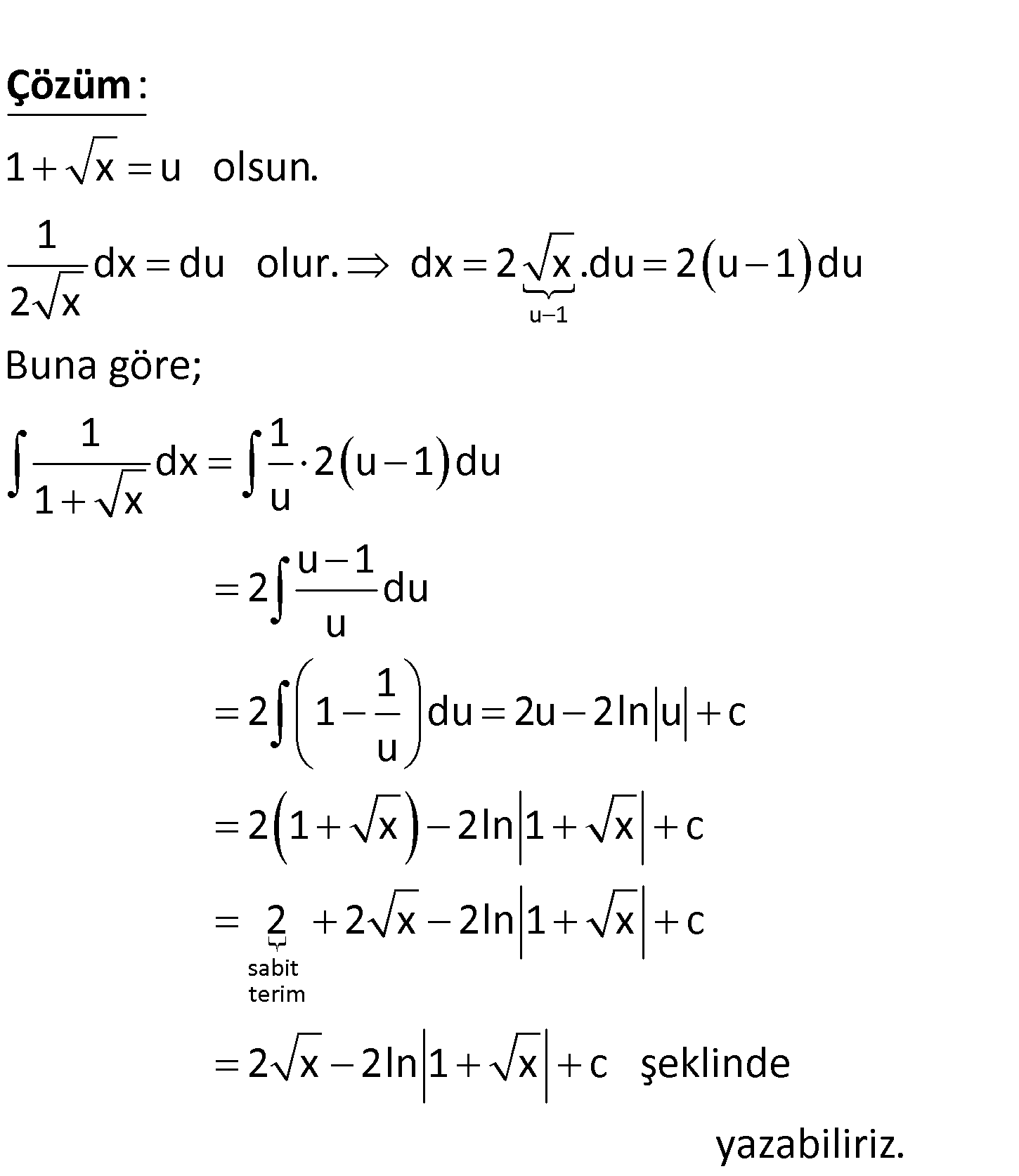
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3 3 3 2 3 x x x dx işleminin sonucu nedir? 1 1 2 1 A) x x x x c B) x x x c 3 4 3 3 2 1 C) x x x x c D) 3 3 2 3 3 2 3 x x x x c 5 4 2 3 E) x x x c 5 4 www.matematikkolay.net 1 3 1 2 2 1 3 3 Köklü sayıları, üslü sayı şeklinde yazarsak daha kolay çözeriz. x x x .x x dir. x x t : Çözüm 3 1 3 2 3 3 1 1 1 2 3 5 4 2 3 5 4 2 3 ür. Buna göre; x x x dx x x dx x x c 3 1 1 1 2 3 x x c 5 4 2 3 2 3 x x c 5 4 1 1 2 2 3 2 3 2 3 x .x x.x c 5 4 2 3 x x x x c buluruz. 5 4 65
www.matematikkolay.net 3 3 3 3 2x 3 dx x işleminin sonucu nedir? 4 A) 4 x 6 x c B) x 6 x c 3 4 4 C) x 3 x c D) x 6 x c 3 3 3 4 E) 6 x x c 3 1 2 1 1 2 2 2x 3 2x 3 dx dx dx x x x 3 2 x dx dx x 2x dx 3x dx : Çözüm 3 1 2 2 3 3 x x 2 3 c 3 1 2 2 2 2 x 3 2 x c 3 4 x 6 x c buluruz. 3 115
www.matematikkolay.net 2 x x 2 dx ? 2 2 x x 2 dx 2 x 2 : u Çözüm x 2 2 u 2 dx du x 2 u dx du dir. x x x 2 dx x u .u x 3 2 2 3 2 du u u du c 3 (x 2) u x 2 c bulunur. 3 58
www.matematikkolay.net 2 m 3 m 3 m 3 m 1 m 3 m 1 3 (m 1)x dx x 1 işleminin sonucu kaçtır? A) m x 1 c B) m (x 1) c m m C) (x 1) c D) (x 3 4 m m 3 m 1 1) c m E) (x 1) c 3 2 2 m 3 1 3 m 3 2 2 2 3 (m 1)x (m 1)x dx dx x 1 (x 1) du x 1 u olsun. 3x dx du x dx tür. 3 (m 1)x (x : 1 Çözüm 1 m 1 1 m m 1 1 1 m m 1 1 m du (m 1) 3 1 dx dx (m 1) u du 3 ) (u) 1 (m 1) u (m 1) u du C 3 3 1 1 m (m 1) u (m 1) C 3 1 m m 1 1 m.u m 3 m 1 1 m 1 1 m m m m 1 m 3 m 1 C m m m u C u C u C 3 3 3 m (x 1) C buluruz. 3 www.matematikkolay.net 41
www.matematikkolay.net 1 dx 1 x işleminin sonucu nedir? A) 2 x 2ln(1 x) c B) 2 x 2ln(1 x) c C) ln(1 x) c D) ln x 1 c E) x ln(1 x) c u 1 1 x u olsun. 1 dx du olur. dx 2 x .du 2 u 1 du 2 x Buna göre; 1 1 dx 2 u 1 du 1 x u : Çözüm sabit terim u 1 2 du u 1 2 1 du 2u 2ln u c u 2 1 x 2ln 1 x c 2 2 x 2ln 1 x c 2 x 2ln 1 x c şeklinde yazabiliriz. 135

