Soru Sor sayfası kullanılarak Belirli İntegral konusu altında U dönüşümü ile belirli integral, Değişken değiştirerek belirli integral çözme ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

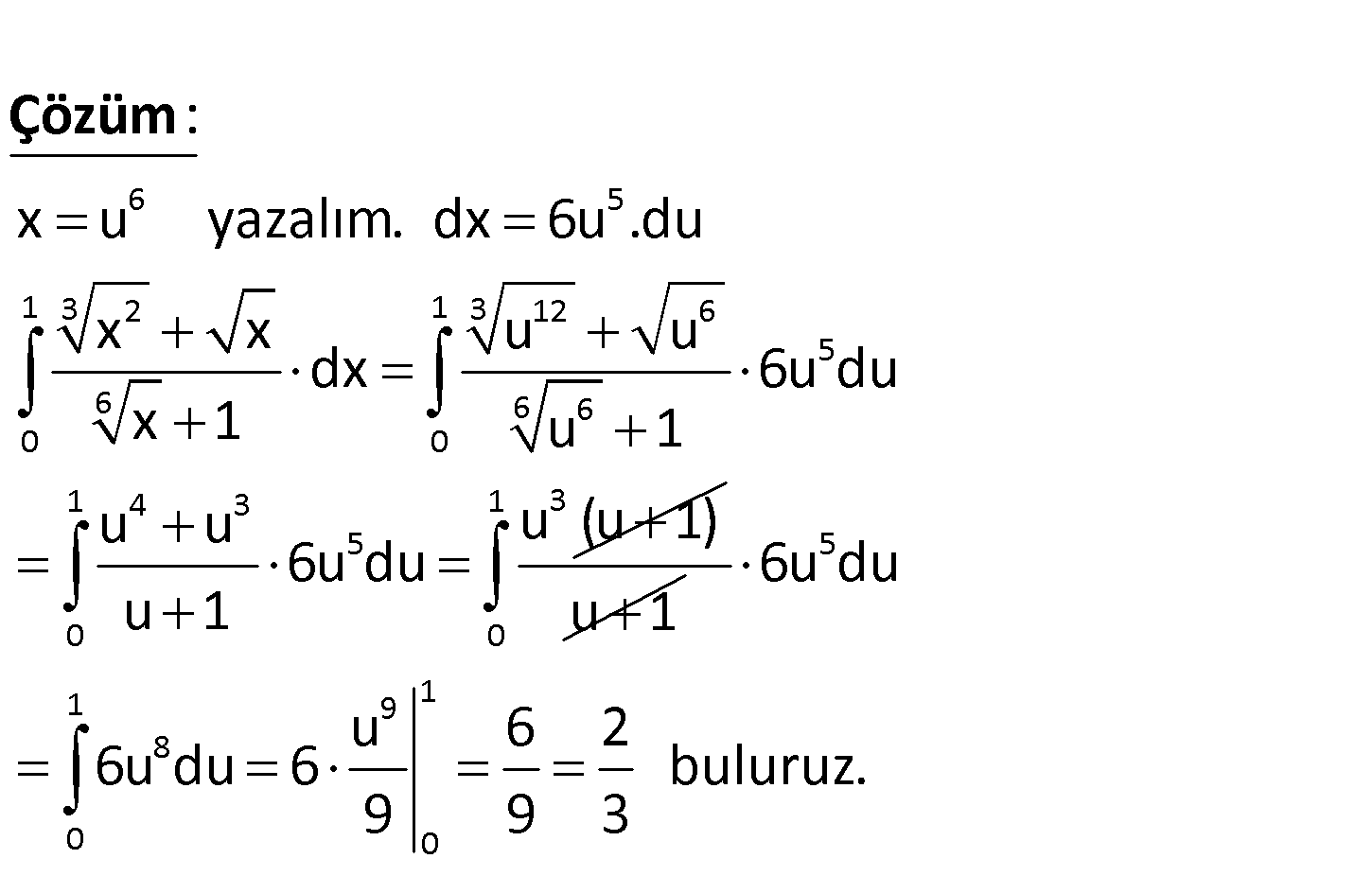
2.SORU
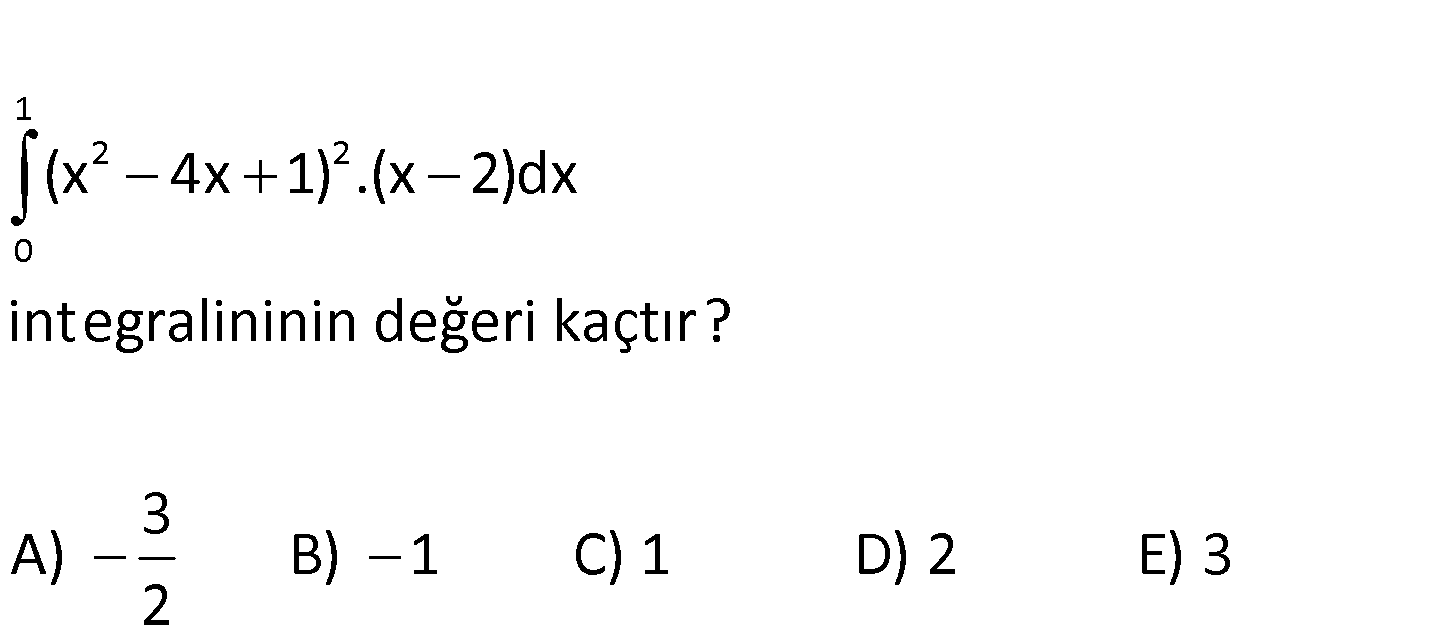

3.SORU


4.SORU

5.SORU
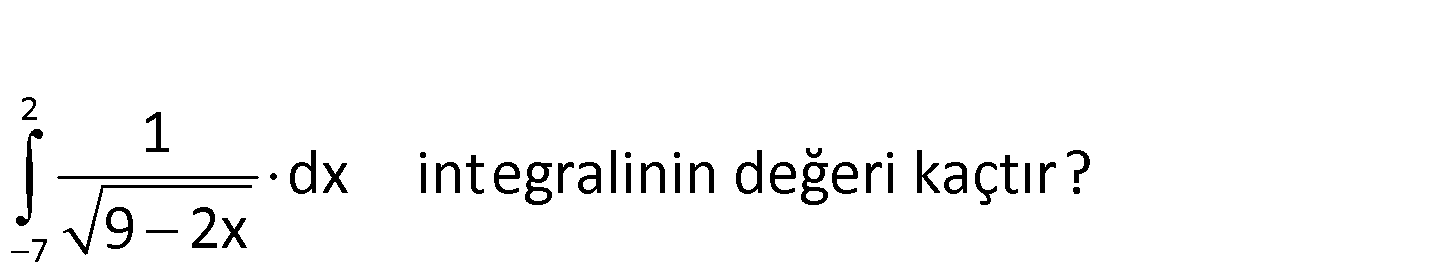
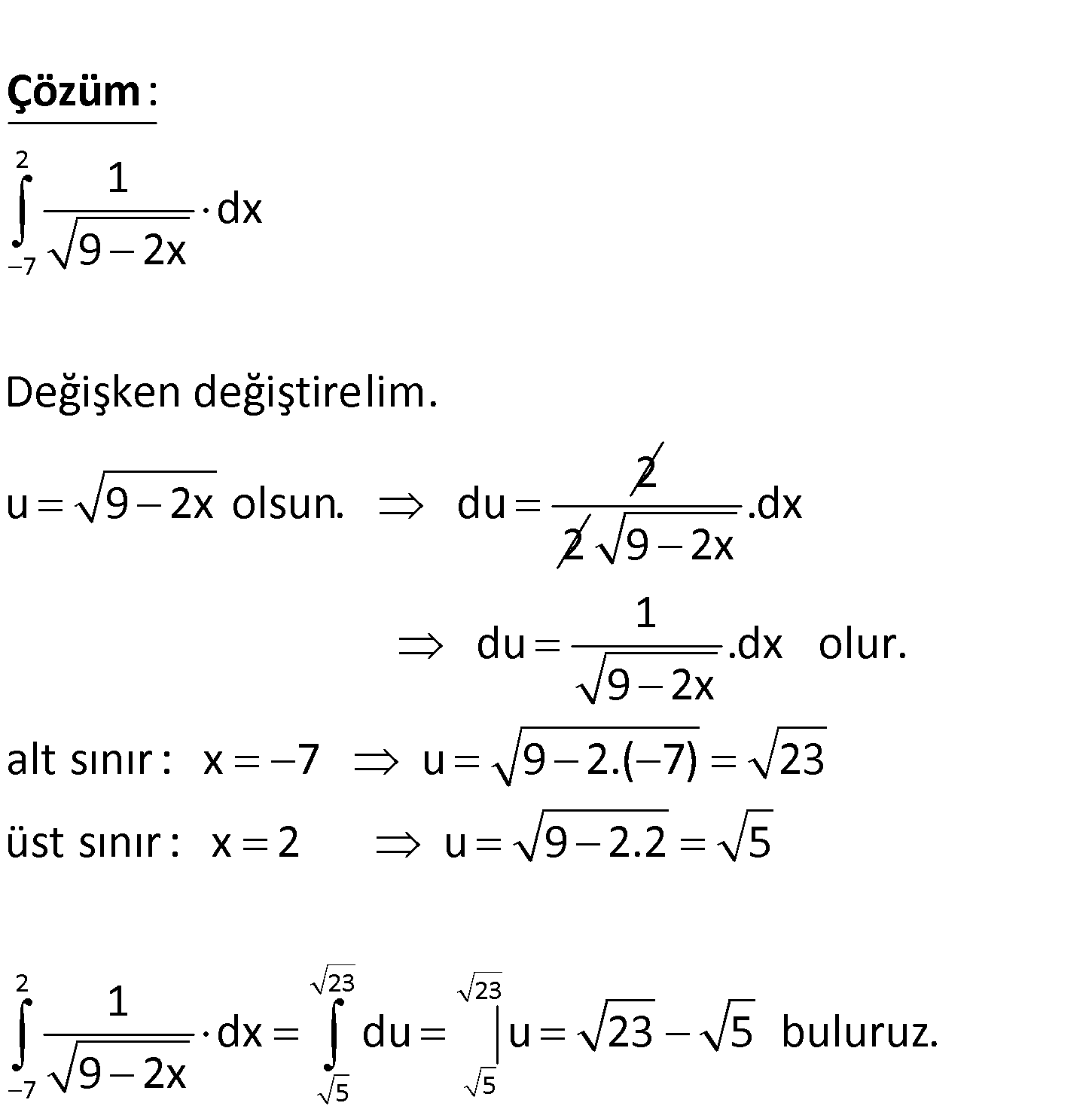
Burdan sonraki sorular, Fen Lisesi Müfredatı için geçerlidir.
6.SORU


7.SORU
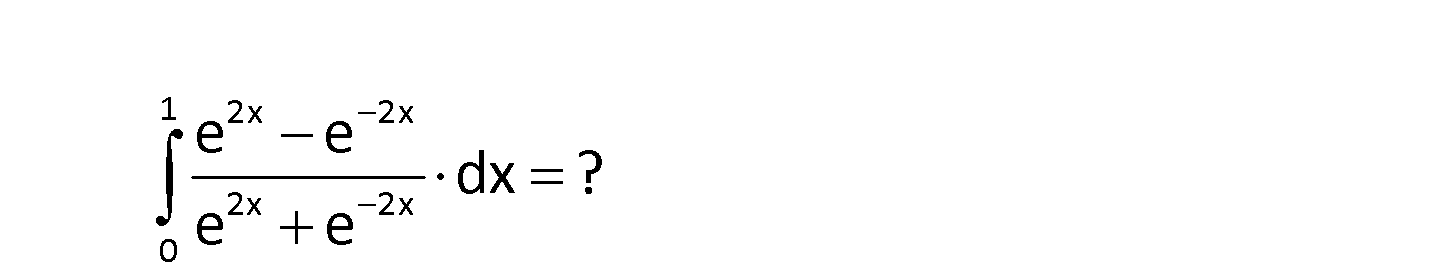

8.SORU

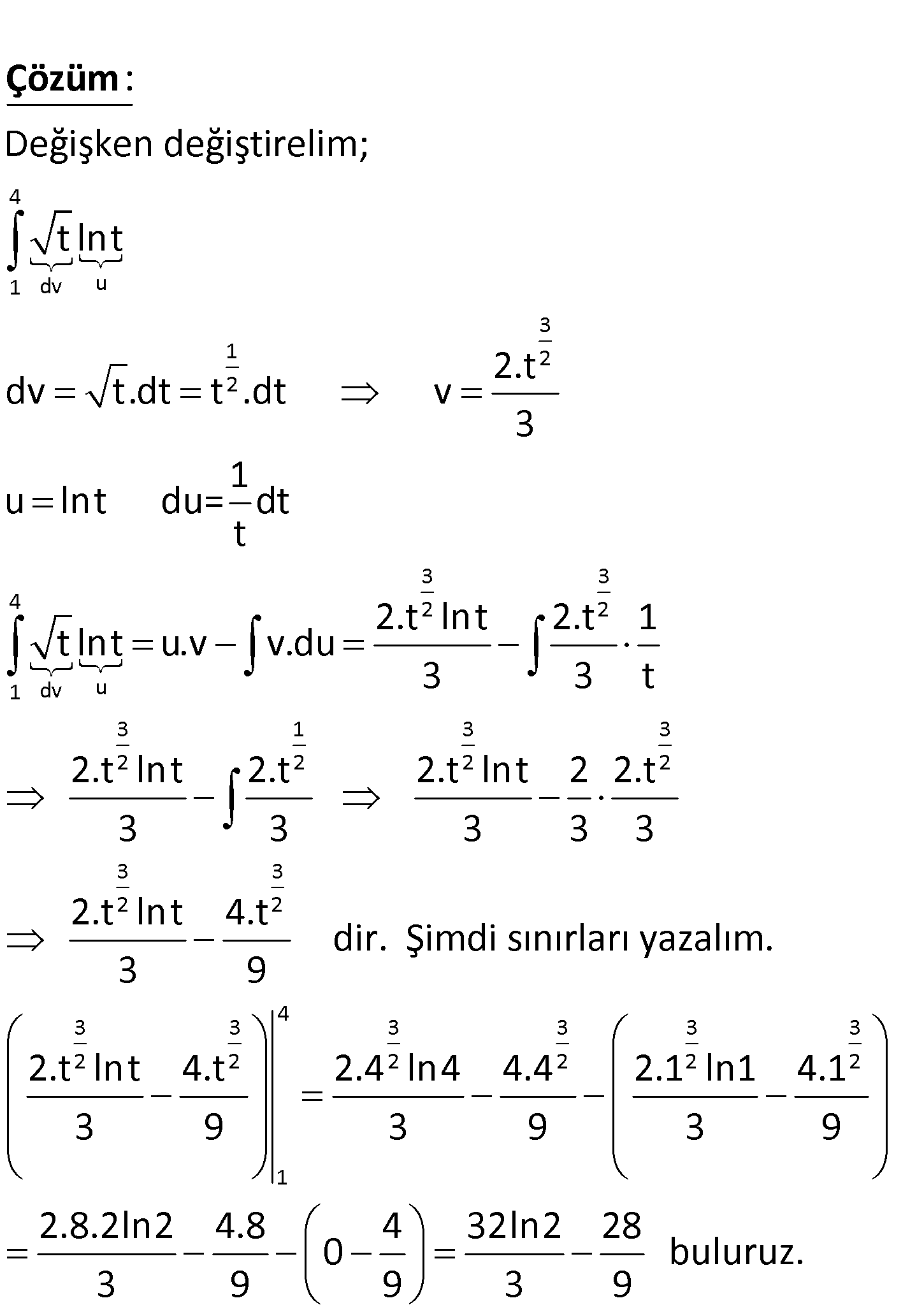
9.SORU
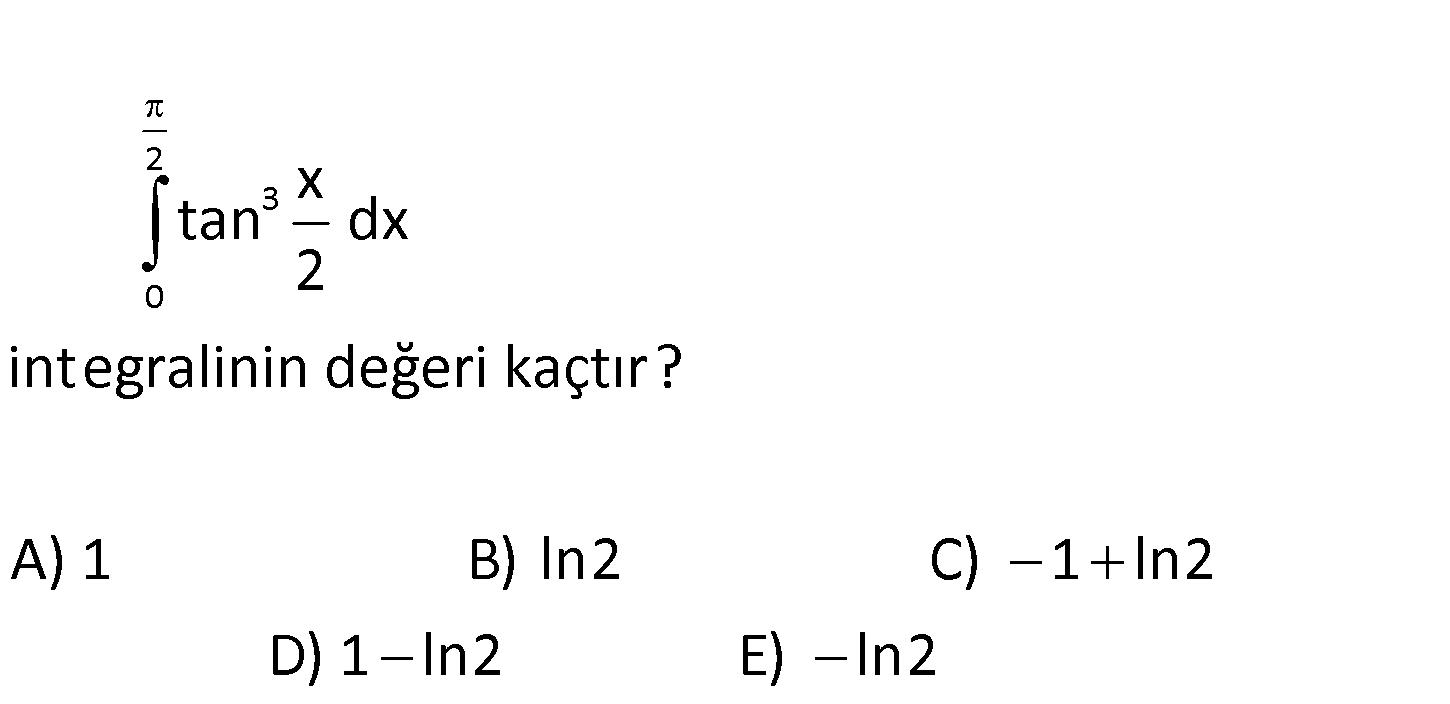
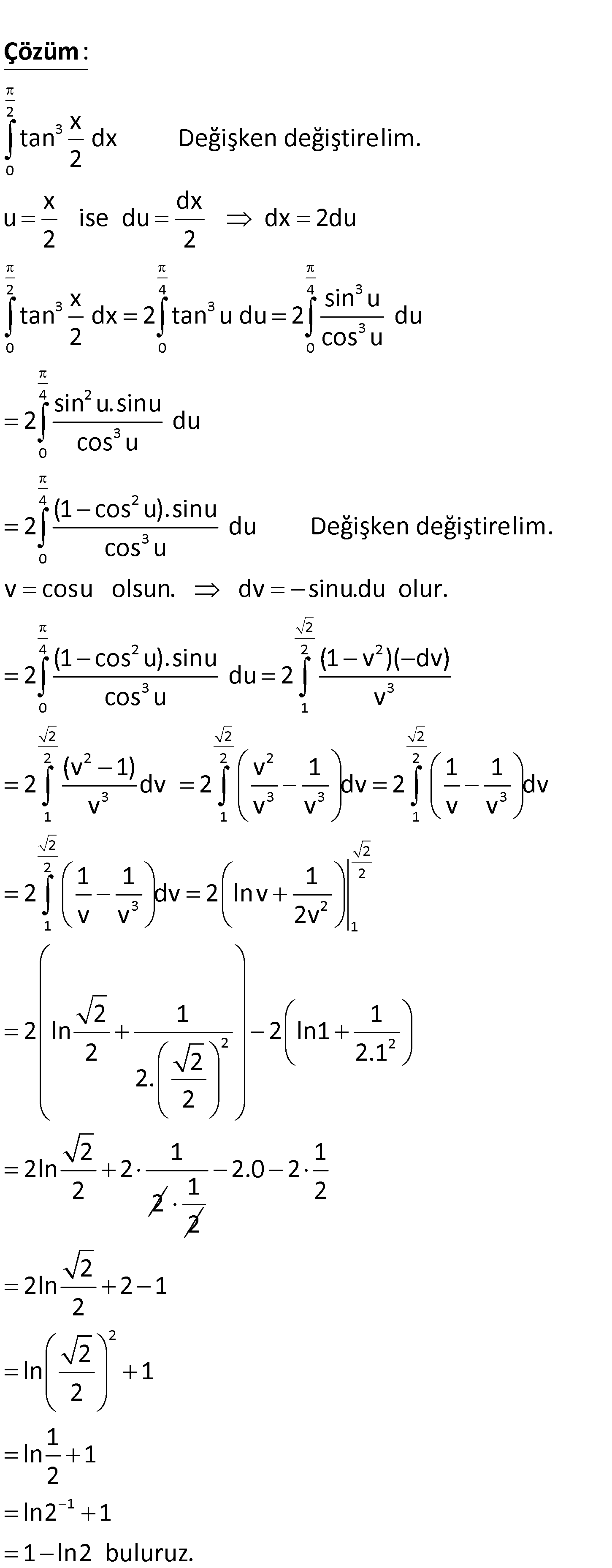
10.SORU

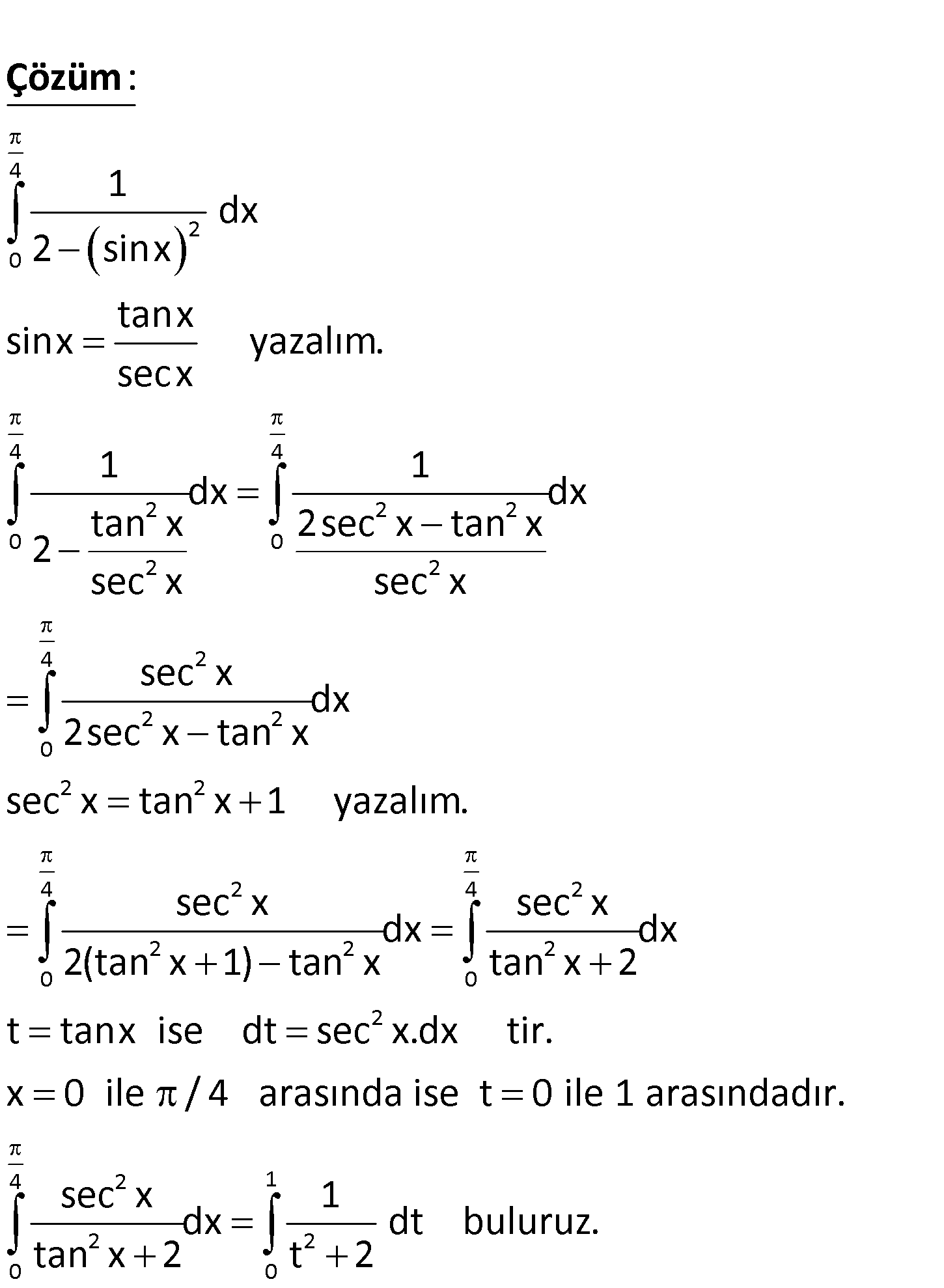
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net 1 3 2 6 0 x x dx x 1 integralinin değeri aşağıdakilerden hangisidir? 6 5 4 3 2 A) B) C) D) E) 7 6 5 4 3 6 6 6 5 1 3 2 3 12 6 6 0 : Payda x 1 değil de x 1 olmalıydı. x u yazalım. dx 6u .du x x u u dx x 1 u Çözüm 1 5 6 6 0 1 4 3 3 5 0 6u du 1 u u u (u 1) 6u du u 1 u1 1 5 0 1 9 1 8 0 0 6u du u 6 2 6u du 6 buluruz. 9 9 3 14
1 2 2 0 (x 4x 1) .(x 2)dx integralininin değeri kaçtır? 3 A) B) 1 C) 1 D) 2 E) 3 2 www.matematikkolay.net 1 2 2 0 2 1 2 2 0 1 1 2 2 0 0 (x 4x 1) .(x 2)dx u x 4x 1 olsun. du 2x 4 olur. (x 4x 1) .(x 2)dx du 1 u . u 2 : 2 Çözüm 3 2 3 1 0 3 3 1 u (x 4x 1) du 2 3 6 (1 4 1) (0 0 1) 8 1 9 3 buluruz. 6 6 6 6 6 2 29
Bir f fonkisyonunun grafiğinin x a noktasındaki teğetinin eğimi 1 ve x b noktasındaki teğetinin eğ a b imi ise 3 tür. f ”(x) ikinci türev fonksiyonu [a, b] aralığında sürekli olduğuna göre, f ‘(x)f ”(x)dx integralinin değeri kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 www.matematikkolay.net a b a a 2 a b b b f ‘(x)f ”(x)dx f ‘(x) u olsun. du f ”(x)dx : olur. u f ‘(x) f ‘(x)f ”(x)dx u.du 2 Çözüm 2:00 AM b 2 2 2 2 2 f ‘(a) f ‘(b) 2 2 1 3 2 2 1 3 2 1 buluruz. 2 2 2 55
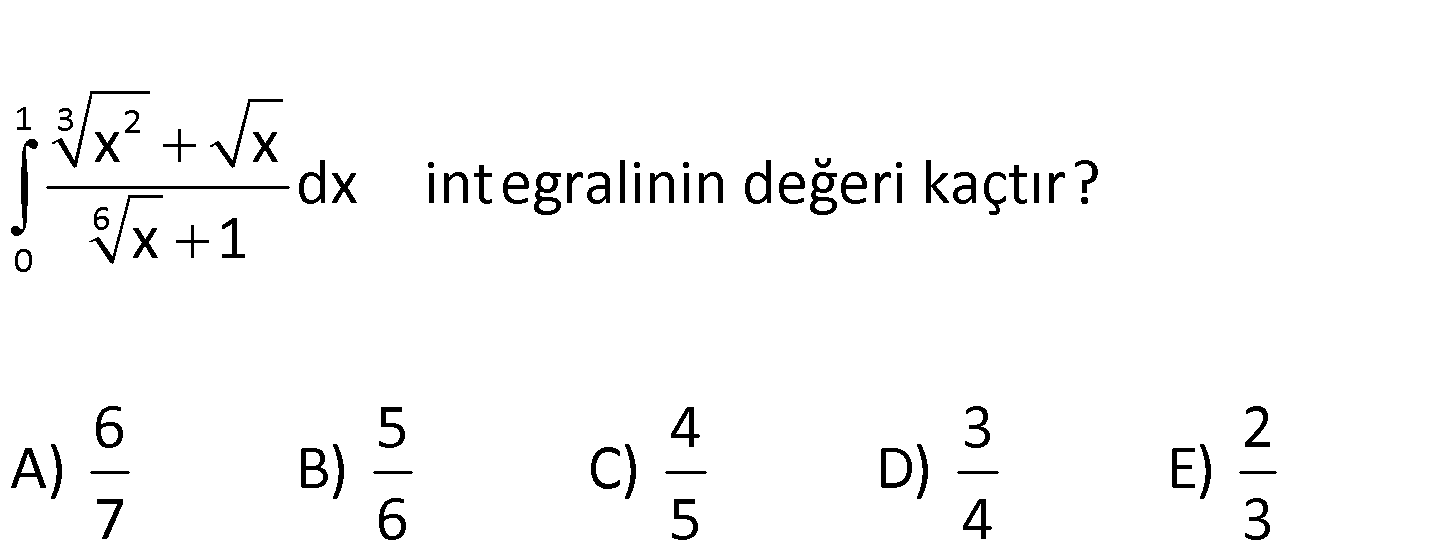
www.matematikkolay.net 1 3 2 6 0 x x dx integralinin değeri kaçtır? x 1 6 5 4 3 2 A) B) C) D) E) 7 6 5 4 3 6 6 6 5 1 3 2 3 12 6 6 0 : x u yazalım. dx 6u .du x x u u dx x 1 u Çözüm 1 5 6 6 0 1 4 3 3 5 0 6u du 1 u u u (u 1) 6u du u 1 u1 1 5 0 1 9 1 8 0 0 6u du u 6 2 6u du 6 buluruz. 9 9 3 80
2 7 1 dx integralinin değeri kaçtır? 9 2x www.matematikkolay.net 2 7 1 dx 9 2x Değişken değiştirelim. 2 u 9 2x olsun : . du Çözüm 2 2 23 23 7 5 5 .dx 9 2x 1 du .dx olur. 9 2x alt sınır : x 7 u 9 2.( 7) 23 üst sınır : x 2 u 9 2.2 5 1 dx du u 23 5 buluruz. 9 2x 82
cosy /2 siny.e dy ? cosy /2 üst alt siny.e dy u cos y olsun; du= sinydy sinydy du olur. u =cos = 1 ve u : Çözüm 1 cosy u /2 0 1 u 1 0 0 cos( / 2) 0 Buna göre; siny.e dy e du e (e e ) 1 1 e 1 1 buluruz. e 2
www.matematikkolay.net 1 2x 2x 2x 2x 0 e e dx ? e e 1 2x 2x 2x 2x 0 4x 2x 2x 2x 2x e e dx e e 1 ln(e 1) x 2 Değişken değiştirelim. u e e olsun. du 2( e : e Çözüm 2 2 2 2 2x 2x 0 0 2 2 1 2x 2x e e e e 2x 2x 0 2 2 2 2 ).dx du (e e ).dx olur. 2 alt sınır : x 0 u e e 2 üst sınır : x 1 u e e e e 1 du 1 dx lnu e e 2 u 2 1 (ln(e e ) ln2) 2 2 2 4 4 2 2 2 4 1 1 (ln(e ) ln2) 2 e 1 e 1 1 (ln( ) ln2) (ln(e 1) lne ln2) 2 e 2 1 ( 2 ln2 ln(1 e ) buluruz. 2 4
www.matematikkolay.net 4 1 t lnt.dt 4 1 dv u 3 1 2 2 Değişken değiştirelim; t lnt 2.t dv t.dt t .dt v 3 1 u lnt du= d t : Çözüm 3 3 4 2 2 1 dv u 3 1 3 3 2 2 2 2 3 3 2 2 4 3 3 3 3 3 3 2 2 2 2 2 2 1 t 2.t lnt 2.t 1 t lnt u.v v.du 3 3 t 2.t lnt 2.t 2.t lnt 2 2.t 3 3 3 3 3 2.t lnt 4.t dir. Şimdi sınırları yazalım. 3 9 2.t lnt 4.t 2.4 ln4 4.4 2.1 ln1 4.1 3 9 3 9 3 9 2.8.2ln2 4.8 4 32ln2 28 0 buluruz. 3 9 9 3 9 6
www.matematikkolay.net 2 3 0 x tan dx 2 integralinin değeri kaçtır? A) 1 B) ln2 C) 1 ln2 D) 1 ln2 E) ln2 www.matematikkolay.net 230230 xtan dx Değişken değiştirelim. 2xdxu ise du dx2du 22:xtan dx2ta2Çözüm344330024302430222423301sinunu du2 ducosusinu.sinu2 ducosu(1cosu).sinu2 du Değişken değiştirelim.cosuvcosu olsun. dvsinu.du olur.(1cosu).sinu(1v)(dv)2 du2 cosuv22222222233331112222321122(v1)v111dv 2dv2dvvvvvv1112dv2lnvvv2v2112ln2ln122.122.2212ln222122112.02222ln2122ln121ln12ln211ln2 www.matematikkolay.net 7
www.matematikkolay.net 4 2 0 1 dx 2 sin x integralinde t tanx dönüşümü yapılırsa aşağıdaki – lerden hangisi elde e 1 2 1 2 2 0 1 0 2 1 2 2 1 0 dilir? 1 1 1 A) dt B) dt C) dt t 1 1 t t 2 1 1 D) dt E) dt t 2 1 t www.matematikkolay.net 4 2 0 4 4 2 2 2 0 0 2 2 2 1 dx 2 sinx tanx sinx yazalım. secx 1 1 dx dx tan x 2sec x tan x 2 sec x sec x sec x 2 : Çözüm 4 2 2 0 2 2 4 2 4 2 2 2 2 0 0 2 4 2 2 2 0 dx sec x tan x sec x tan x 1 yazalım. sec x sec x dx dx 2(tan x 1) tan x tan x 2 t tanx ise dt sec x.dx tir. x 0 ile / 4 arasında ise t 0 ile 1 arasındadır. sec x 1 dx tan x 2 t 2 1 0 dt buluruz. 66

