Soru Sor sayfası kullanılarak Belirli İntegral konusu altında Riemann, Alt Toplam, Üst Toplam, İntegralin hangi aralıkta olduğunu bulma, İntegralin yaklaşık değerini bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU

3.SORU
4.SORU

5.SORU


6.SORU
7.SORU
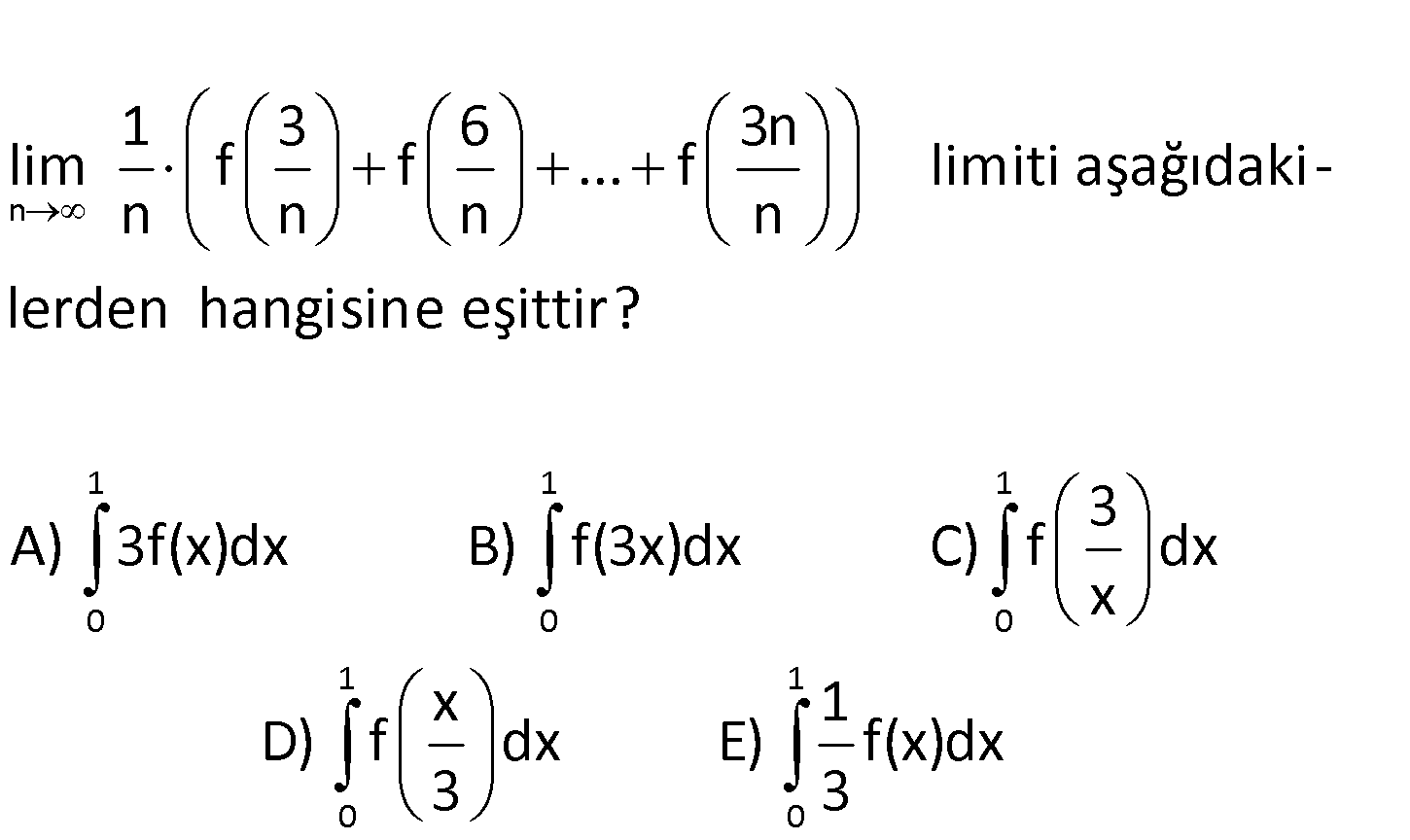
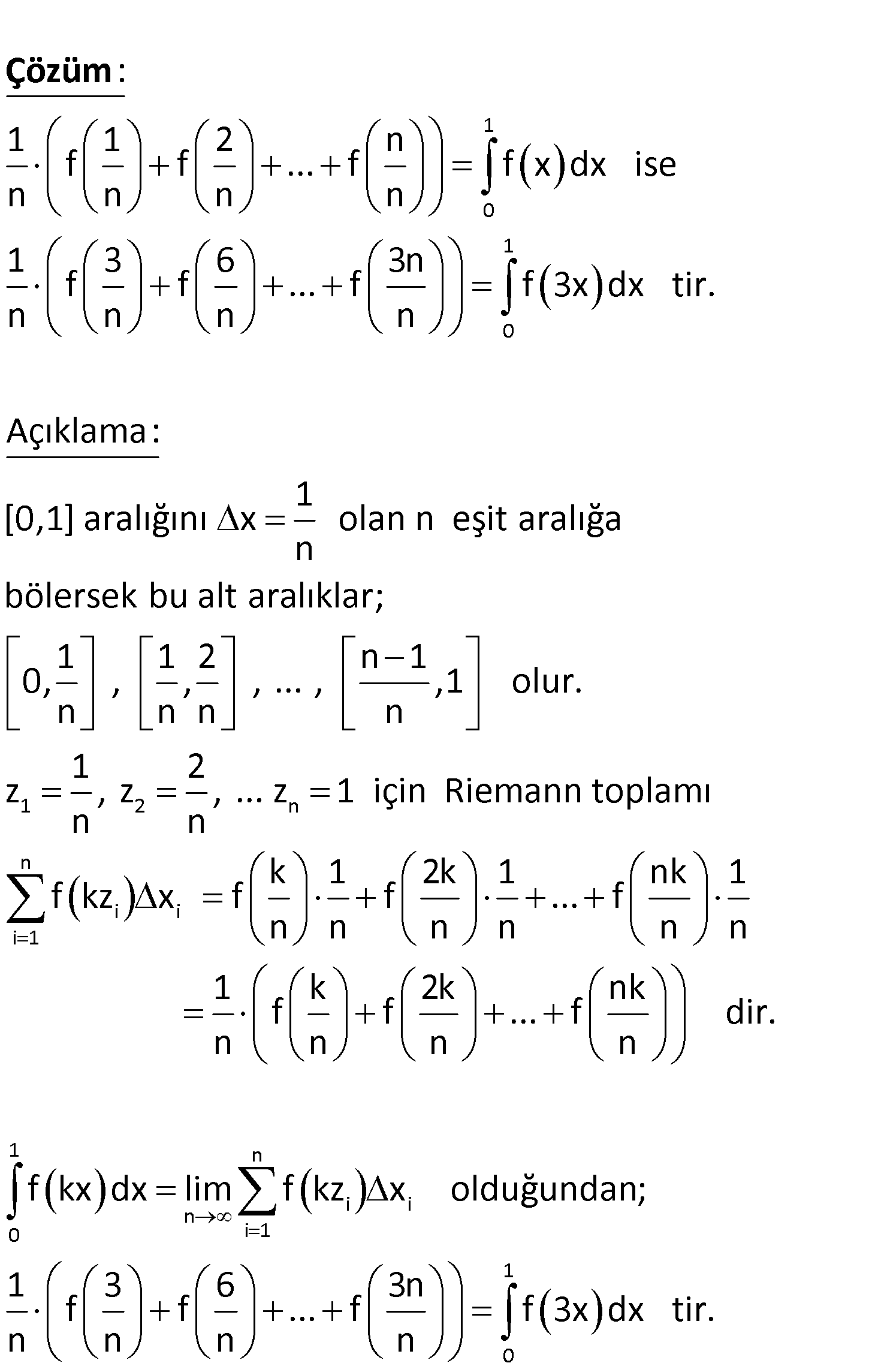
8.SORU

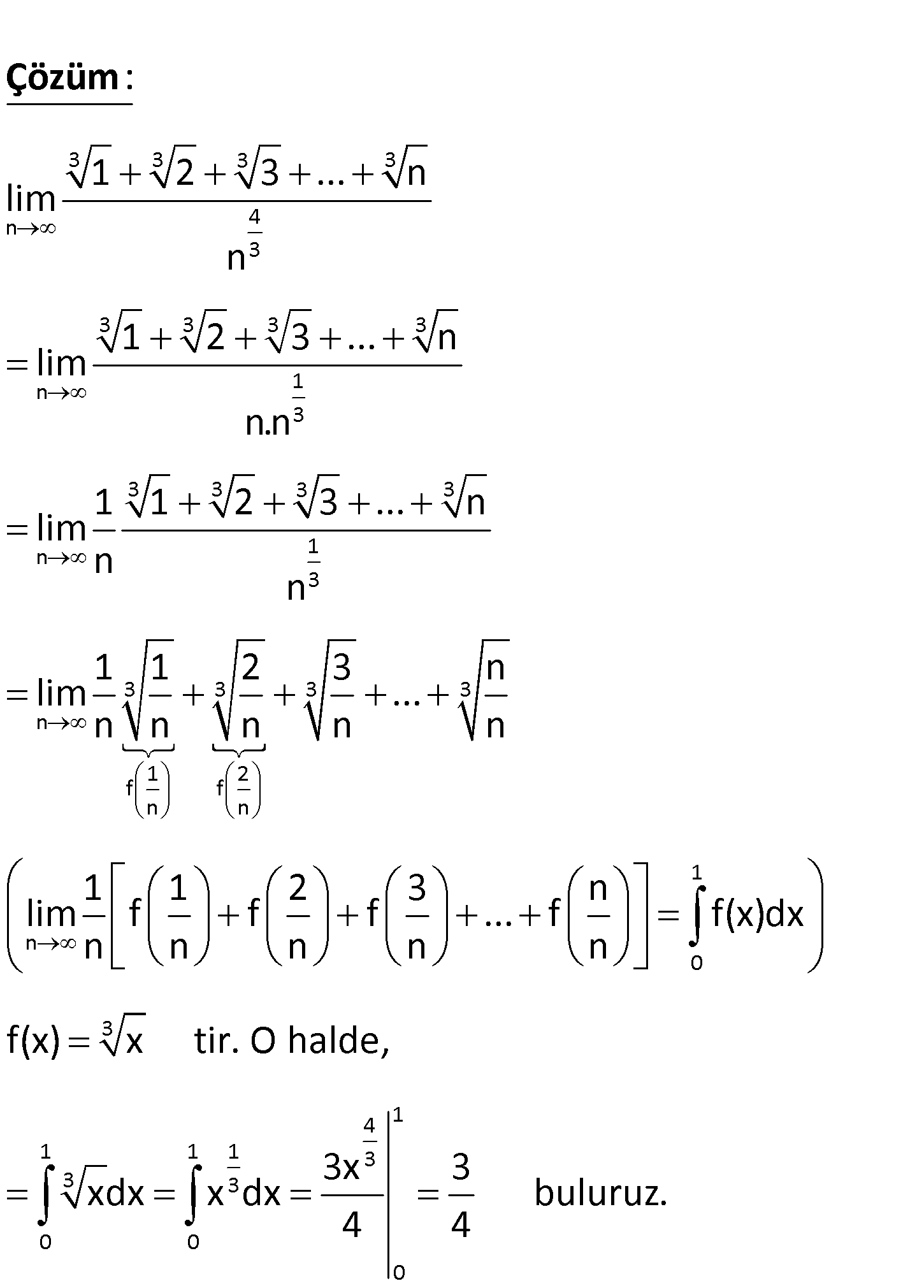
9.SORU


10.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
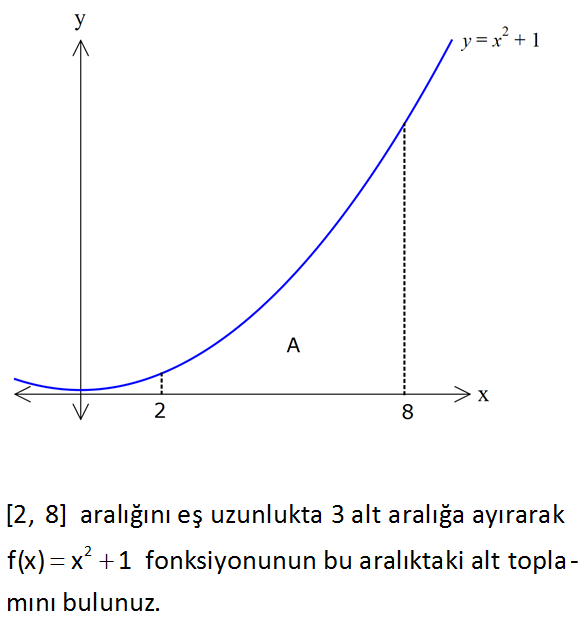
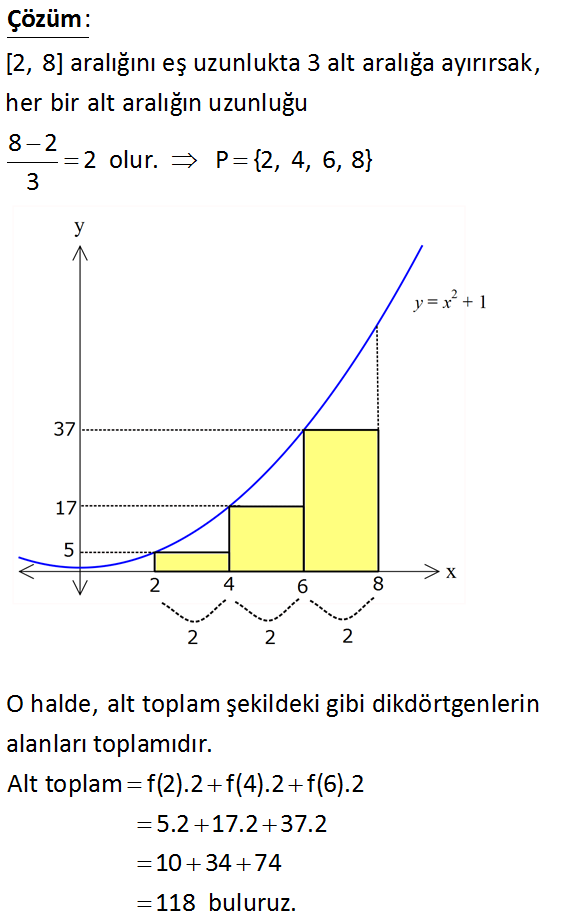
Riemann Alt Toplam 2 [2, 8] aralığını eş uzunlukta 3 alt aralığa ayırarak f(x) x 1 fonksiyonunun bu aralıktaki alt toplamını bulunuz. www.matematikkolay.net : [2, 8] aralığını eş uzunlukta 3 alt aralığa ayırırsak, her bir alt aralığın uzunluğu 8 2 2 3 Çözüm olur. P {2, 4, 6, 8} O halde, alt toplam şekildeki gibi dikdörtgenlerin alanları toplamıdır. Alt toplam f(2).2 f(4).2 f(6).2 5.2 17.2 37.2 10 34 74 118 buluruz. 87
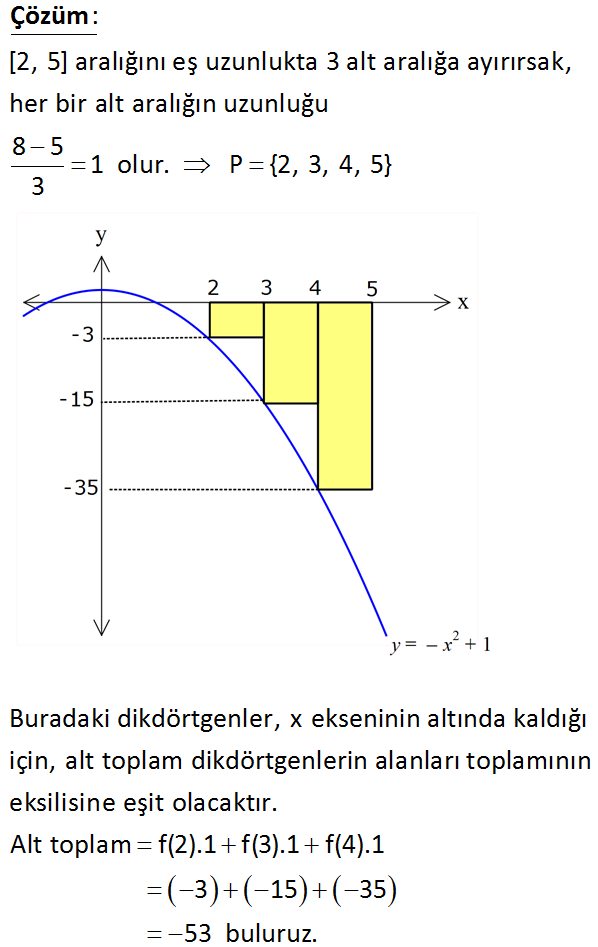
Rieman Alt negatif sonuç www.matematikkolay.net 2 [2, 5] aralığını eş uzunlukta 3 alt aralığa ayırarak f(x) x 1 fonksiyonunun bu aralıktaki alt toplamını bulunuz. www.matematikkolay.net : [2, 5] aralığını eş uzunlukta 3 alt aralığa ayırırsak, her bir alt aralığın uzunluğu 8 5 1 3 Çözüm olur. P {2, 3, 4, 5} Buradaki dikdörtgenler, x ekseninin altında kaldığı için, alt toplam dikdörtgenlerin alanları topla mının eksilisine eşit olacaktır. Alt toplam f(2).1 f(3).1 f(4).1 3 15 35 53 buluruz. 88
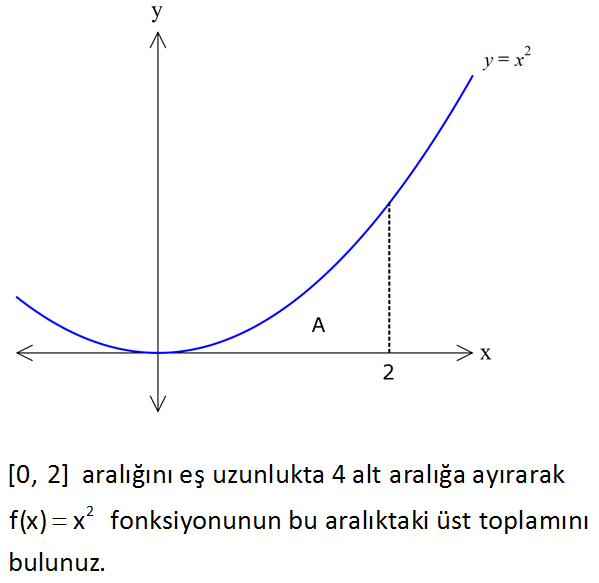
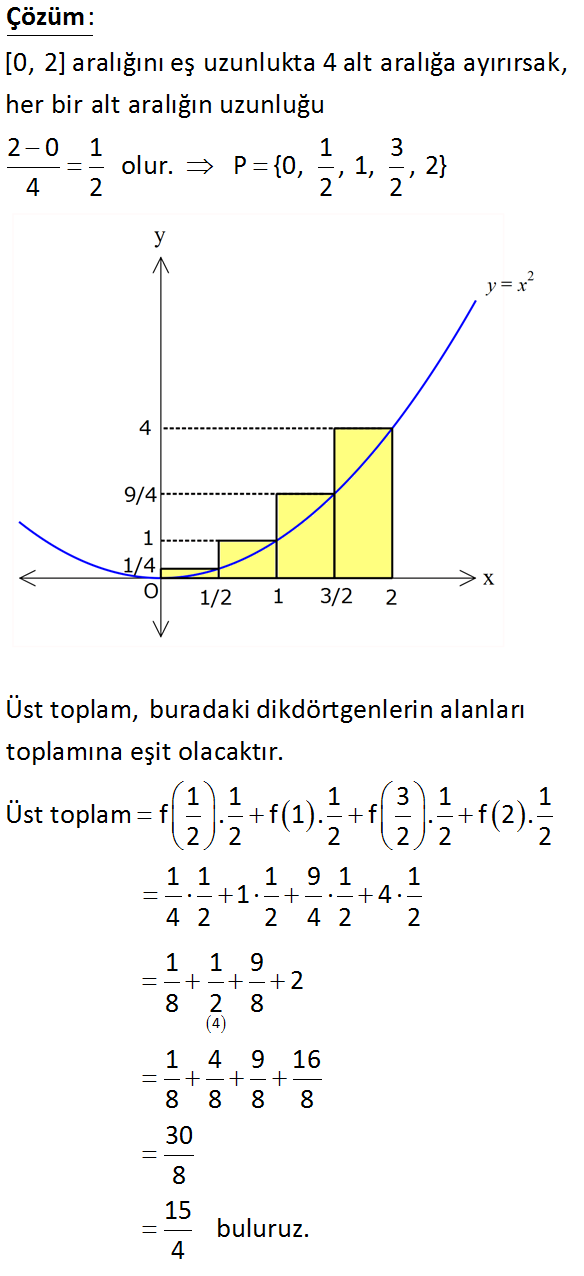
Üst Toplam www.matematikkolay.net 2 [0, 2] aralığını eş uzunlukta 4 alt aralığa ayırarak f(x) x fonksiyonunun bu aralıktaki üst toplamını bulunuz. www.matematikkolay.net : [0, 2] aralığını eş uzunlukta 4 alt aralığa ayırırsak, her bir alt aralığın uzunluğu 2 0 1 4 2 Çözüm 1 3 olur. P {0, , 1, , 2} 2 2 Üst toplam, buradaki dikdörtgenlerin alanları toplamına eşit olacaktır. 1 1 Üst toplam f . f 1 . 2 2 4 1 3 1 1 f . f 2 . 2 2 2 2 1 1 1 9 1 1 1 4 4 2 2 4 2 2 1 1 9 2 8 2 8 1 4 9 16 8 8 8 8 30 8 15 buluruz. 4 www.matematikkolay.net 89
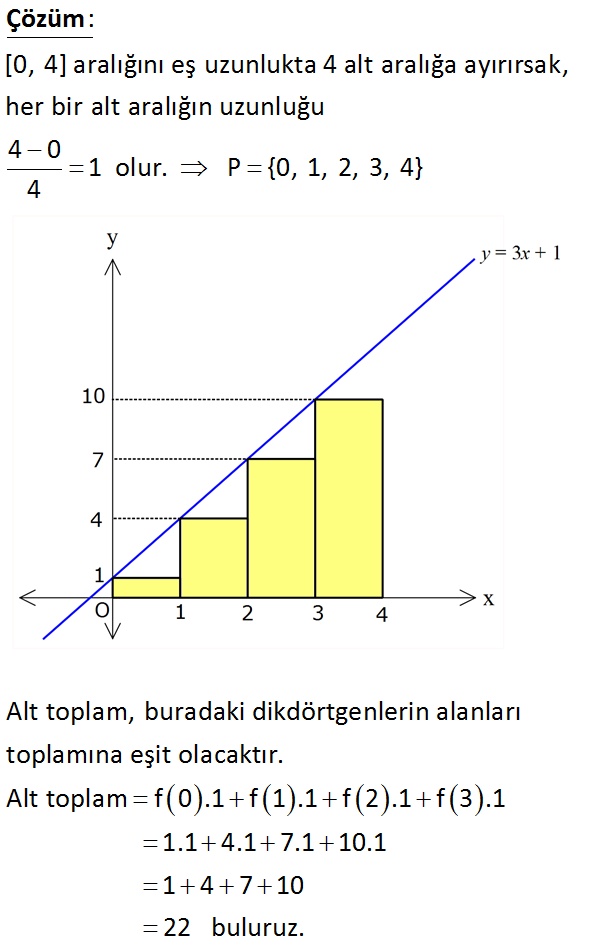
f : [0, 4] R, y 3x 1 fonksiyonu veriliyor. [0, 4] aralığını 4 eşit parçaya bölen bölüntüye göre f f onksiyonunun Riemann alt toplamını bulunuz. A) 18 B) 20 C) 22 D) 24 E) 26 www.matematikkolay.net : [0, 4] aralığını eş uzunlukta 4 alt aralığa ayırırsak, her bir alt aralığın uzunluğu 4 0 1 4 Çözüm olur. P {0, 1, 2, 3, 4} Alt toplam, buradaki dikdörtgenlerin alanları toplamına eşit olacaktır. Alt toplam f 0 .1f 1 .1f 2 .1f 3.1 1.1 4.1 7.1 10.1 1 4 7 10 22 buluruz. 90
www.matematikkolay.net 3 y x 2 eğrisini [0, 3] aralığında 3 eşit parçaya bölen bölüntüye göre Riemann alt toplamın, üst to plama oranını kaçtır? 7 9 11 13 A) 1 B) C) D) E) 13 29 27 22 : [0, 3] aralığını eş uzunlukta 3 alt aralığa ayırırsak, her bir alt aralığın uzunluğu 3 0 1 3 Çözüm olur. P {0, 1, 2, 3} Alt Toplam f(0).1 f(1).1 f(2).1 f(3).1 2.1 3.1 10.1 29.1 2 3 10 29 44 tür. Üst Toplam f(1).1 f(2).1 f(3).1 f(4) .1 3.1 10.1 29.1 66.1 3 10 29 66 108 dir. 44 11 Oran buluruz. 108 27 www.matematikkolay.net 91
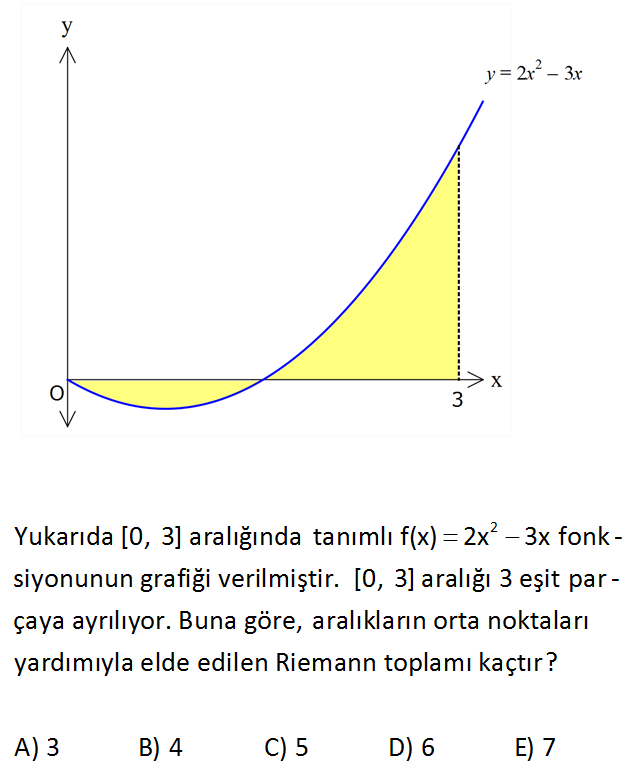
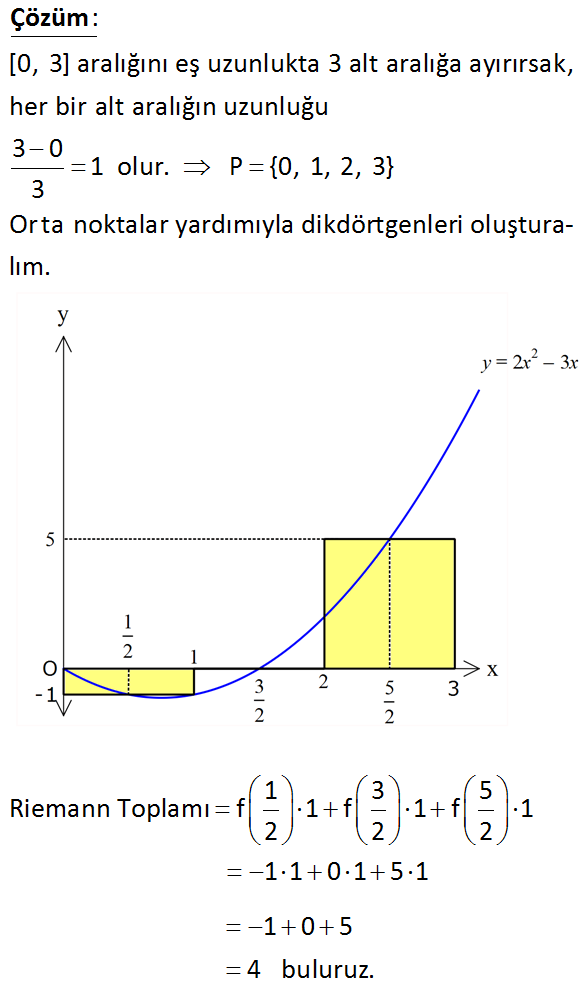
2 Yukarıda [0, 3] aralığında tanımlı f(x) 2x 3x fonk – siyonunun grafiği verilmiştir. [0, 3] aralığı 3 eşit par – çaya ayrılıyor. Buna göre, aralıkların orta noktaları yardımıyla elde edilen Riemann toplamı kaçtır? A) 3 B) 4 C) 5 D) 6 E) 7 www.matematikkolay.net : [0, 3] aralığını eş uzunlukta 3 alt aralığa ayırırsak, her bir alt aralığın uzunluğu 3 0 1 3 Çözüm olur. P {0, 1, 2, 3} Or ta noktalar yardımıyla dikdörtgenleri oluşturalım. 1 3 5 Riemann Toplamı f 1 f 1 f 1 2 2 2 1 1 0 1 5 1 1 0 5 4 buluruz. 92
www.matematikkolay.net n 1 3 6 3n lim f f … f limiti aşağıdaki – n n n n lerden hangisine eşittir? A 1 1 1 0 0 0 1 1 0 0 3 ) 3f(x)dx B) f(3x)dx C) f dx x x 1 D) f dx E) f(x)dx 3 3 www.matematikkolay.net 1 0 1 1 2 n f f … f f x dx ise n n n n 1 3 6 3n f f … f n n n n : Çözüm 1 0 1 2 n f 3x dx tir. Açıklama: 1 [0,1] aralığını x olan n eşit aralığa n bölersek bu alt aralıklar; 1 1 2 n 1 0, , , , … , ,1 olur. n n n n 1 2 z , z , … z 1 için Riemann toplamı n n n i i i 1 1 n i i n 0 i 1 k 1 2k 1 nk 1 f kz x f f … f n n n n n n 1 k 2k nk f f … f dir. n n n n f kx dx lim f kz x olduğundan; 1 3 6 f f … n n n 1 0 3n f f 3x dx tir. n 79
www.matematikkolay.net 1 n 0 1 1 2 3 n lim f f f … f f(x)dx n n n n n olduğu Riemann toplamından bili 3 3 3 3 n 4 3 ndiğine göre, 1 2 3 … n lim n limitinin değeri kaçtır? 4 3 2 1 1 A) B) C) D) E) 3 4 3 2 3 3 3 3 3 n 4 3 3 3 3 3 n 1 3 3 3 3 3 n 1 3 3 n 1 f 1 2 3 … n lim n 1 2 3 … n lim n.n 1 1 2 3 … n lim n n 1 1 lim n : n Çözüm 3 3 3 2 f n n 1 n 0 3 4 1 1 1 1 3 3 3 0 0 0 2 3 n … n n n 1 1 2 3 n lim f f f … f f(x)dx n n n n n f(x) x tir. O halde, 3x 3 xdx x dx buluruz. 4 4 www.matematikkolay.net 83
www.matematikkolay.net 4 2 0 x 9 dx integrali aşağıdaki aralıklardan hangisindedir? A) [0, 12] B) [18, 20] C) [12, 20] D) [0, 12] E) [15, 24] 4 2 0 2 x 9.dx 0 ile 4 arasında x değeri sürekli pozitiftir. x’in pozitif olduğu aralıkta, 9 : x Çözüm 2 4 4 4 2 2 0 0 0 4 4 4 2 0 0 0 4 2 4 4 2 0 0 0 4 2 0 9 x 6x 9 dur. Dolayısıyla; 9.dx x 9.dx (x 3) .dx dir. 3.dx x 9.dx (x 3).dx x 3x x 9.dx 3x 2 12 x 9.dx 20 dir. Cevap: [12, 20] www.matematikkolay.net 15
2 1 (x 1)dx belirli integralini Riemann ile hesaplayınız. www.matematikkolay.net : [1, 2] aralığını eş uzunlukta n tane alt aralığa ayırırsak, her bir alt aralığın uzunluğu 2 Çözüm n k 1 n n n k 1 k 1 1 1 2 k olur. P {1, 1 , 1 ,…, 1 , …,2} n n n n n k 1 Riemann toplamı f 1 dir. Burada n’i ‘a n n götürürsek, integralin sonucunu bulmuş oluruz. k 1 k lim f 1 lim 1 1 n n n n 1 n n 2 k 1 n n n 2 n k 1 k 1 n t n 2 n 1 n k 2 lim n n k 2 lim lim n n 1 2 … n 2 2 2 lim lim … n n n n ane n 2 n 2 n 2 n n.(n 1) 2 2 lim lim n n n n n lim 2 lim 2 n 1 2 2 5 buluruz. 2

