Soru Sor sayfası kullanılarak Belirli İntegral konusu altında Belirli integralin türevi, İntegralin Türevi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

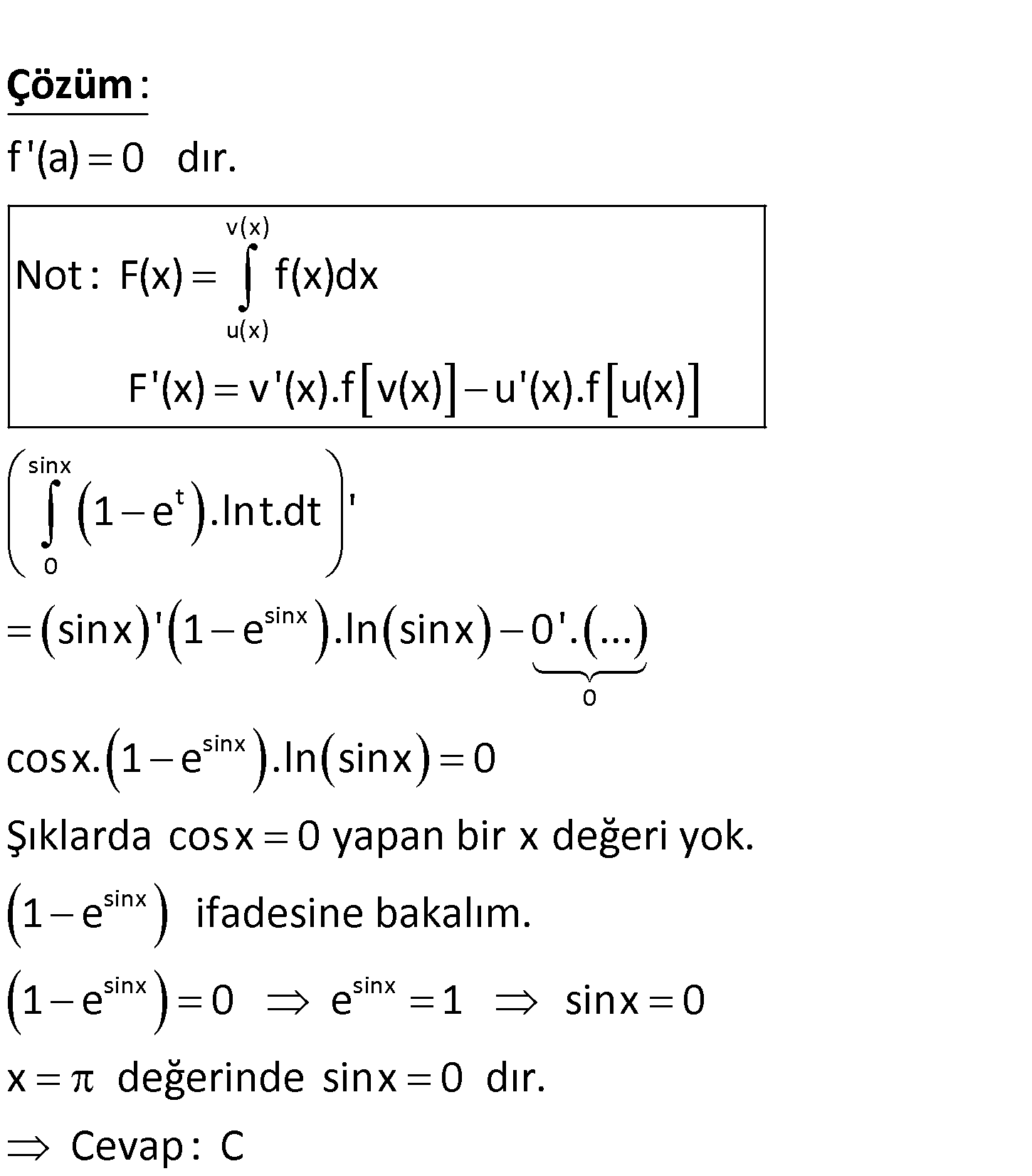
2.SORU
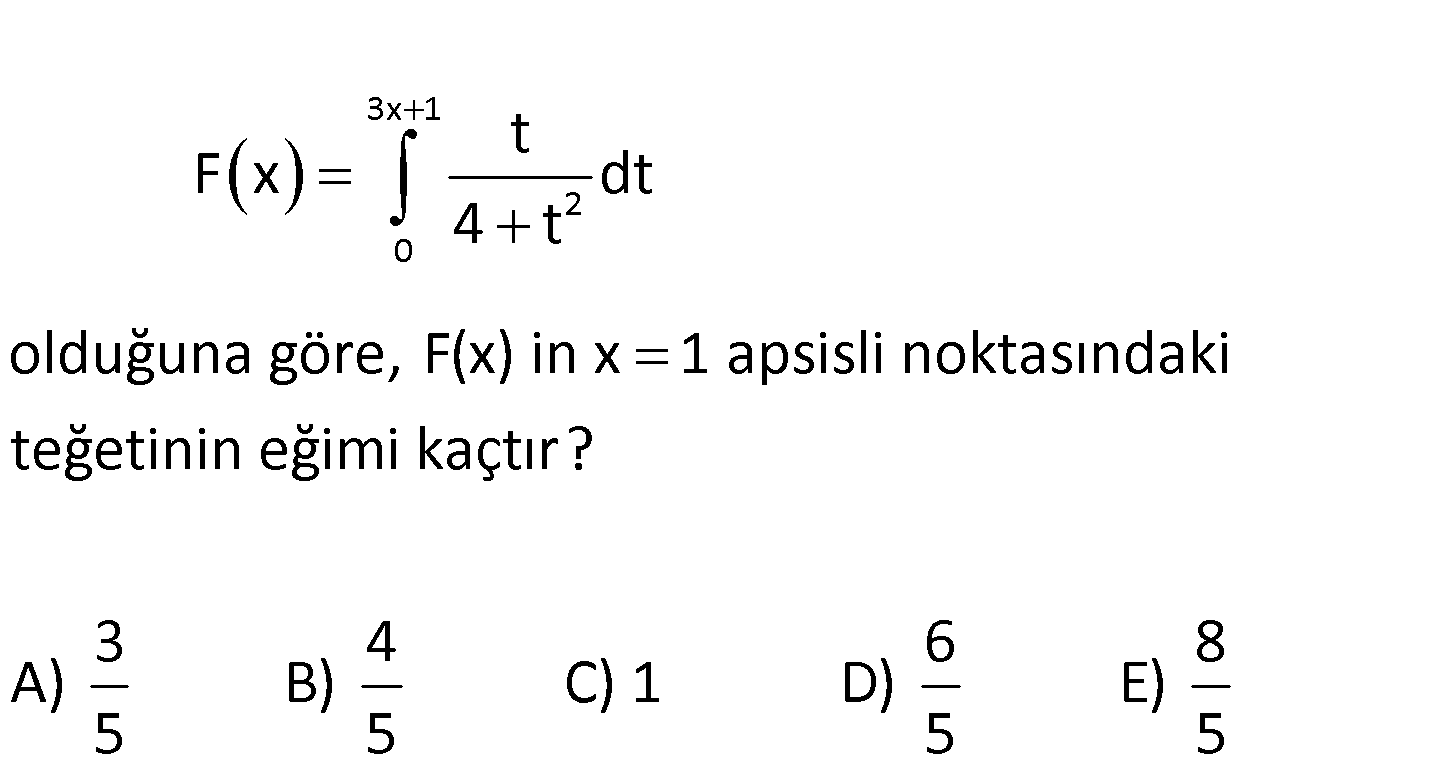
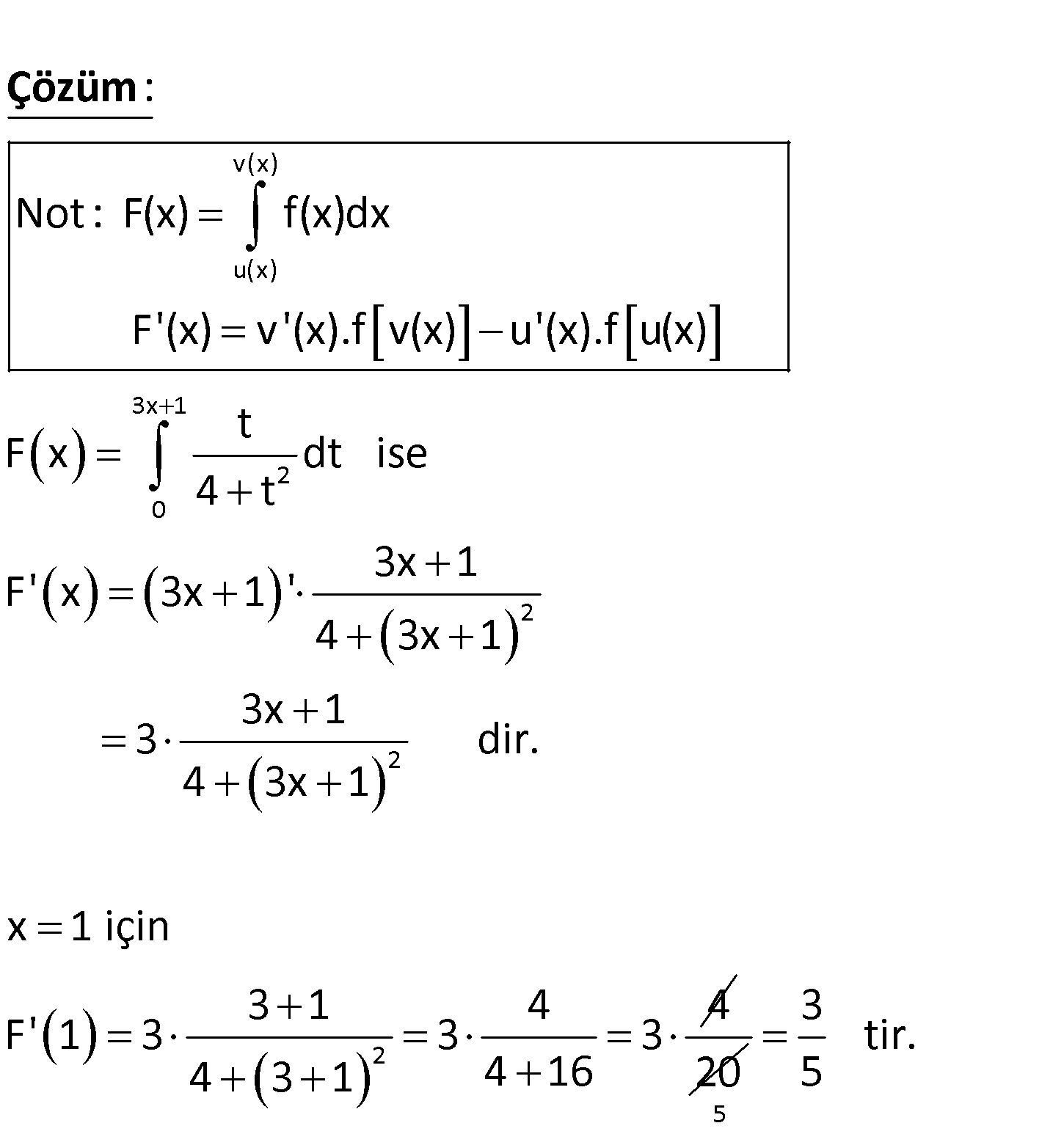
3.SORU
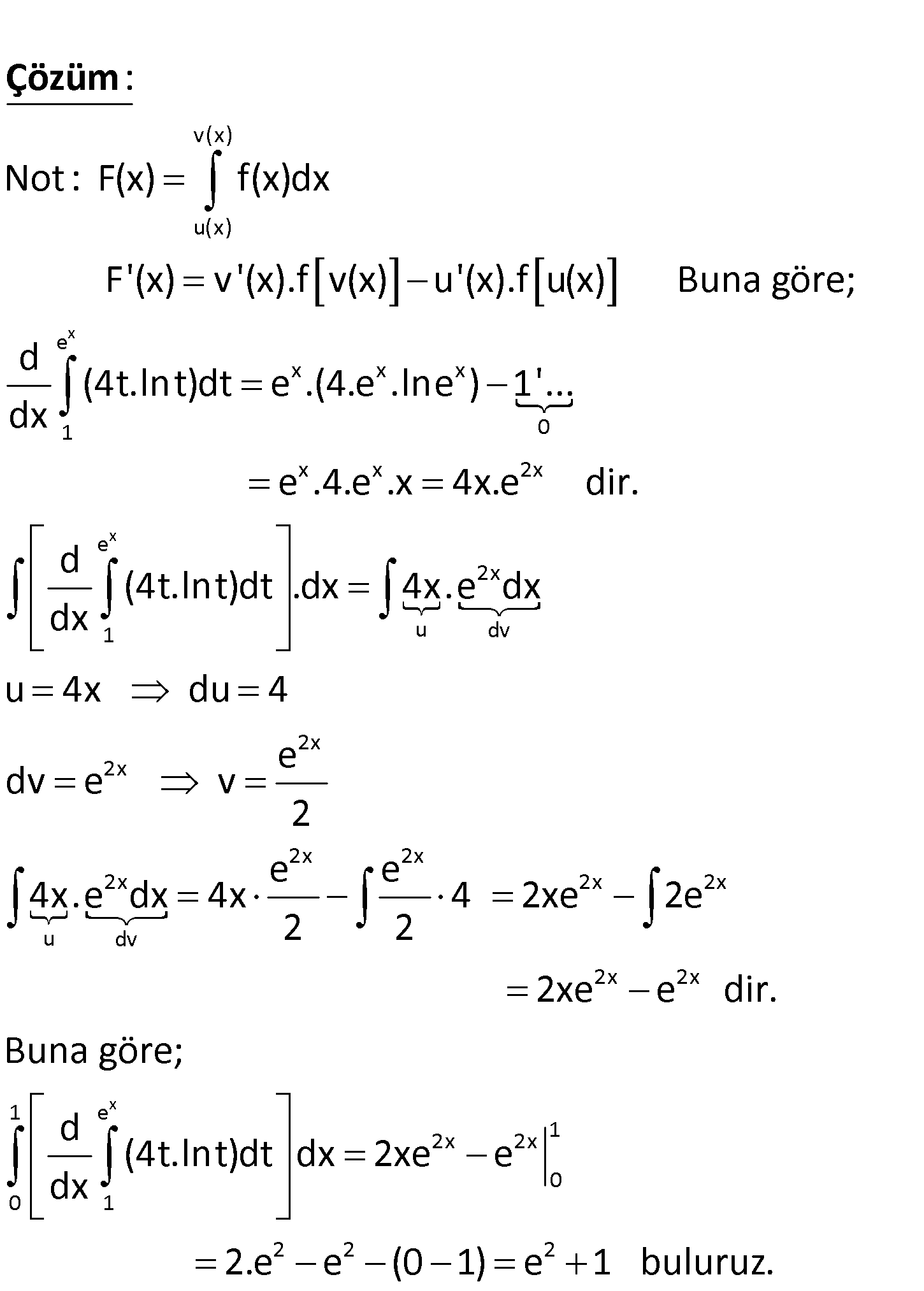
4.SORU
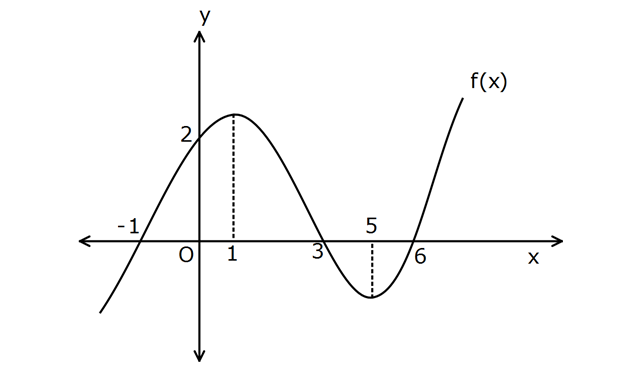


5.SORU
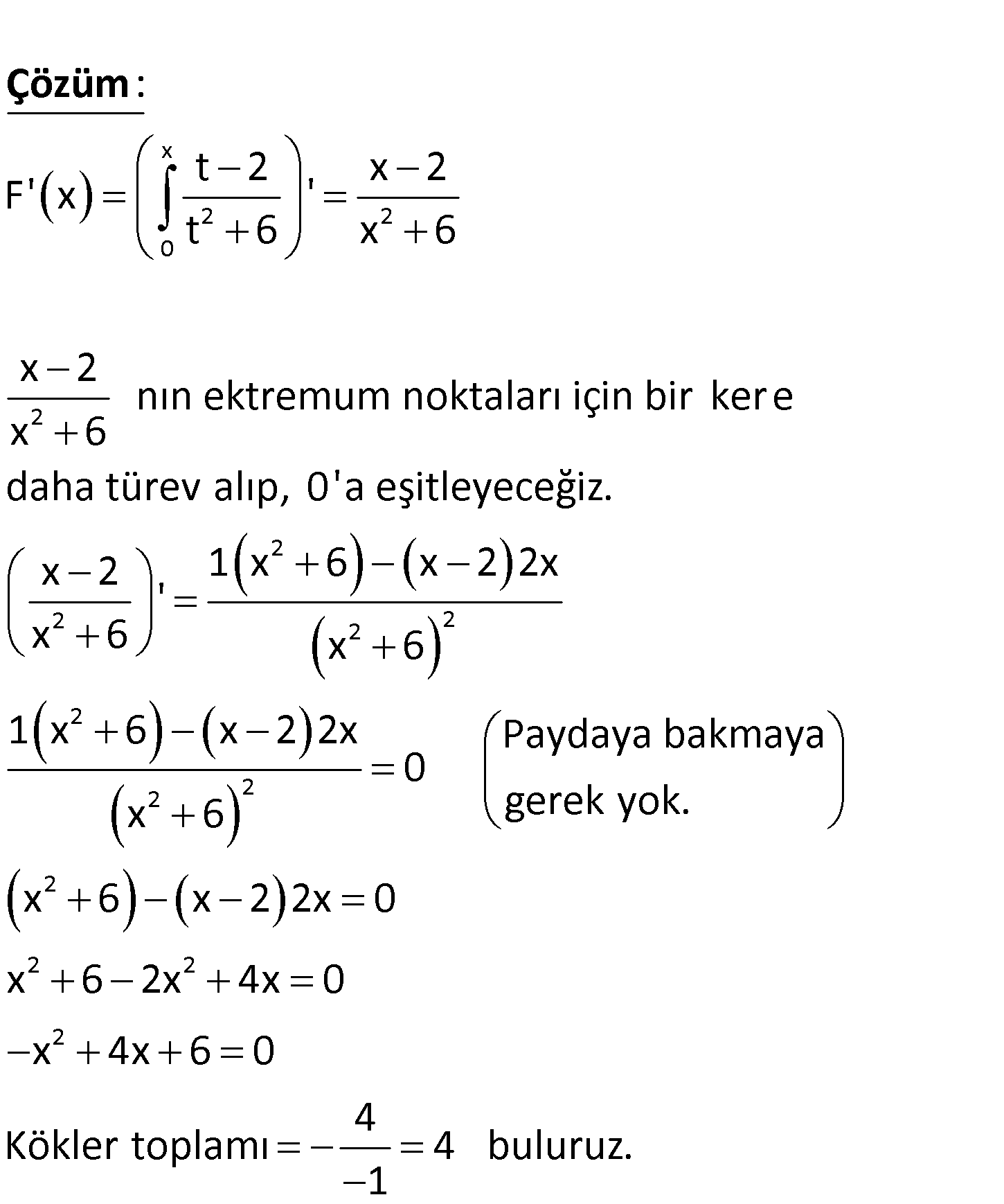
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net sinx t 0 f(x) (1-e )lnt.dt fonksiyonunun x a noktasında bir yerel ekstremumu vardır. Buna göre , a değeri aşağıdakilerden hangisi olabilir? A) B) C) D) 1 E) 2 4 3 v(x) u(x) t f ‘(a) 0 dır. Not : F(x) f(x)dx F'(x) v'(x).f v(x) u'(x).f u(x) : 1 e .lnt Çözüm sinx 0 sinx 0 sinx sinx sinx sinx .dt ‘ sinx ‘ 1 e .ln sinx 0′. … cosx. 1 e .ln sinx 0 Şıklarda cos x 0 yapan bir x değeri yok. 1 e ifadesine bakalım. 1 e 0 e 1 sinx 0 x değerinde sinx 0 dır. Cevap: C 43
3x 1 2 0 t F x dt 4 t olduğuna göre, F(x) in x 1 apsisli noktasındaki teğetinin eğimi kaçt ır? 3 4 6 8 A) B) C) 1 D) E) 5 5 5 5 www.matematikkolay.net v(x) u(x) 3x 1 2 0 Not : F(x) f(x)dx F'(x) v'(x).f v(x) u'(x).f u(x) t F x dt ise 4 t : Çözüm 2 2 2 3x 1 F’ x 3x 1 ‘ 4 3x 1 3x 1 3 dir. 4 3x 1 x 1 için 3 1 4 4 F’ 1 3 3 3 4 3 1 4 16 20 5 3 tir. 5 64
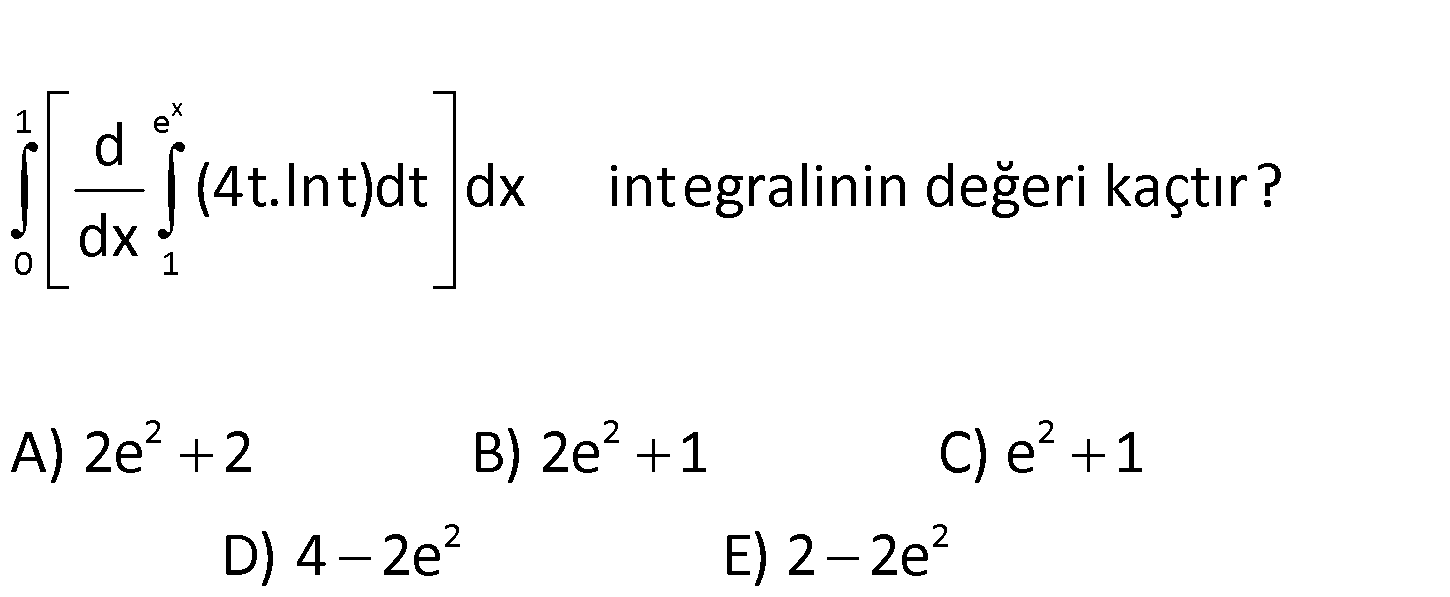
x 1 e 0 1 2 2 2 d (4t.lnt)dt dx integralinin değeri kaçtır? dx A) 2e 2 B) 2e 1 C) e 1 2 2 D) 4 2e E) 22e www.matematikkolay.net v(x) u(x) Not : F(x) f(x)dx F'(x) v'(x).f v(x) u'(x).f u(x) Buna göre; d (4t.lnt) dx : Çözüm x x e x x x 1 0 x x 2x e 2x 1 u dv 2x 2x 2x 2x 2x 2x 2x u dv dt e .(4.e .lne ) 1’… e .4.e .x 4x.e dir. d (4t.lnt)dt .dx 4x.e dx dx u 4x du 4 e dv e v 2 e e 4x.e dx 4x 4 2xe 2e 2 2 x 2x 2x 1 e 2x 2x 1 0 0 1 2 2 2 2xe e dir. Buna göre; d (4t.lnt)dt dx 2xe e dx 2.e e (0 1) e 1 buluruz. 20
www.matematikkolay.net x 0 Şekilde f(x) fonksiyonunun grafiği verilmiştir. g(x) f(t)dt biçiminde tanımlanan g(x) f onksiyonunun yerel maksimum noktasının apsisi kaçtır? A) 1 B) 0 C) 1 D) 3 E) 6 x 0 v(x) u(x) g'(x) 0 f(t)dt ‘ 0 Not : F(x) f(x)dx F'(x) v'(x).f v(x) u'(x).f u(x) : Çözüm x’.f(x) 0′.f 0 0 f(x) 0 x 1,3,6 dan biri olabilir. Hangisi maksimum, hangisi minimum bilmiyoruz. g(x)’in ikinci türevine bakalım. Maksimum noktada ikinci türev negafiftir. g”(x) f ‘(x) tir. Yani f(x) negatif eğimli olmalıdır. 1 ve 6 noktasında pozitif eğimlidir. 3 noktasında negatif eğimlidir. Cevap: x 3 41
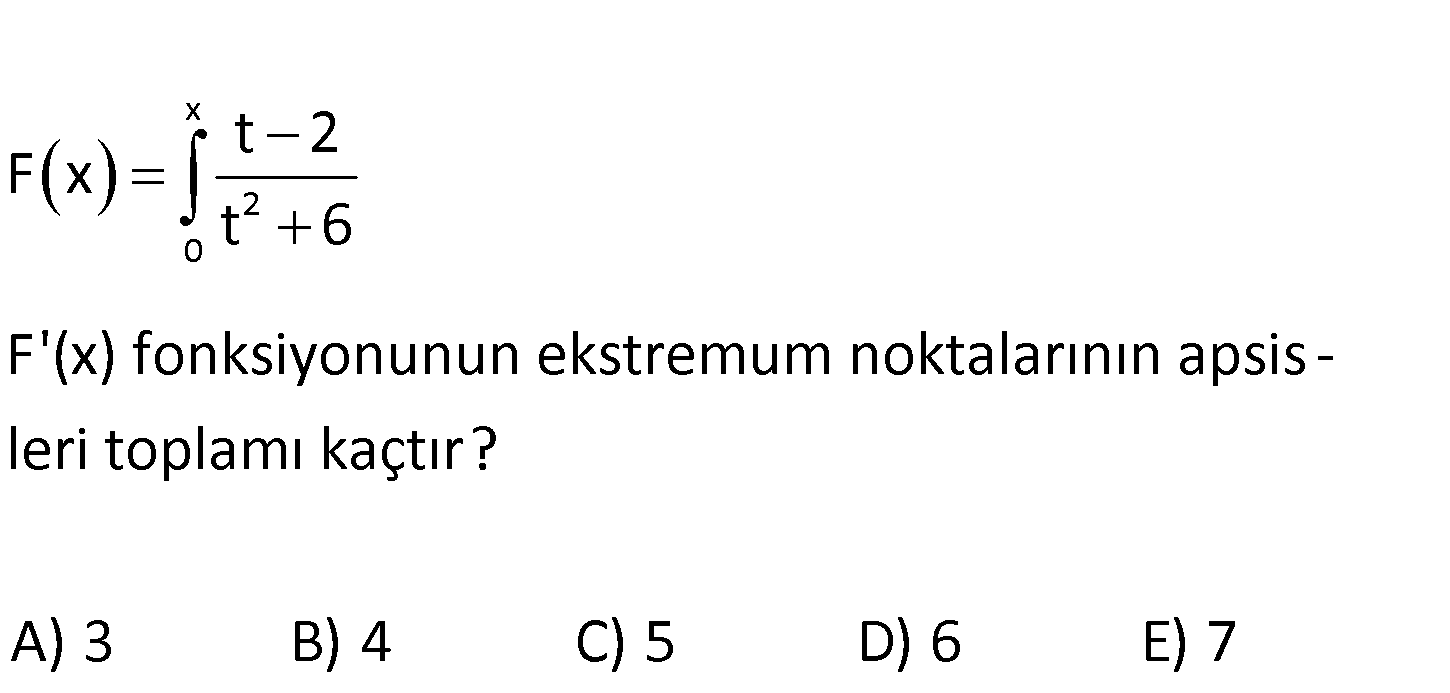
www.matematikkolay.net x 2 0 t 2 F x t 6 F'(x) fonksiyonunun ekstremum noktalarının apsis – leri toplamı kaçtır? A) 3 B) 4 C) 5 D) 6 E) 7 x 2 2 0 2 t 2 x 2 F’ x ‘ t 6 x 6 x 2 nın ektremum noktaları için bir ker e x 6 daha türev alı : p, 0 Çözüm 2 2 2 2 2 2 2 2 2 2 2 ‘a eşitleyeceğiz. x 2 1 x 6 x 2 2x ‘ x 6 x 6 1 x 6 x 2 2x Paydaya bakmaya 0 x 6 gerek yok. x 6 x 2 2x 0 x 6 2x 4x 0 x 4x 6 0 4 Kökler toplamı 4 buluruz. 1 72

