Soru Sor sayfası kullanılarak Ardışık Sayılar konusu altında Harfli ardışık sayı soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
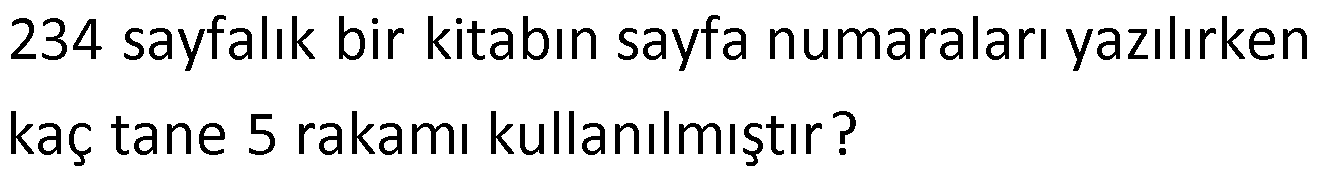

2.SORU
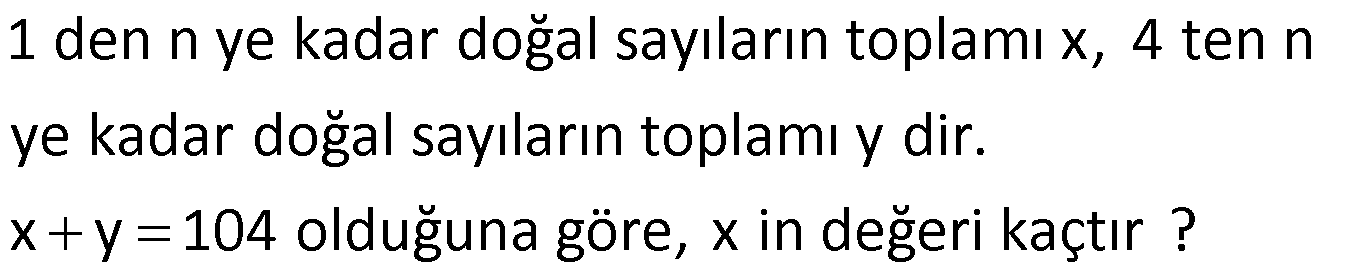

3.SORU

4.SORU


5.SORU
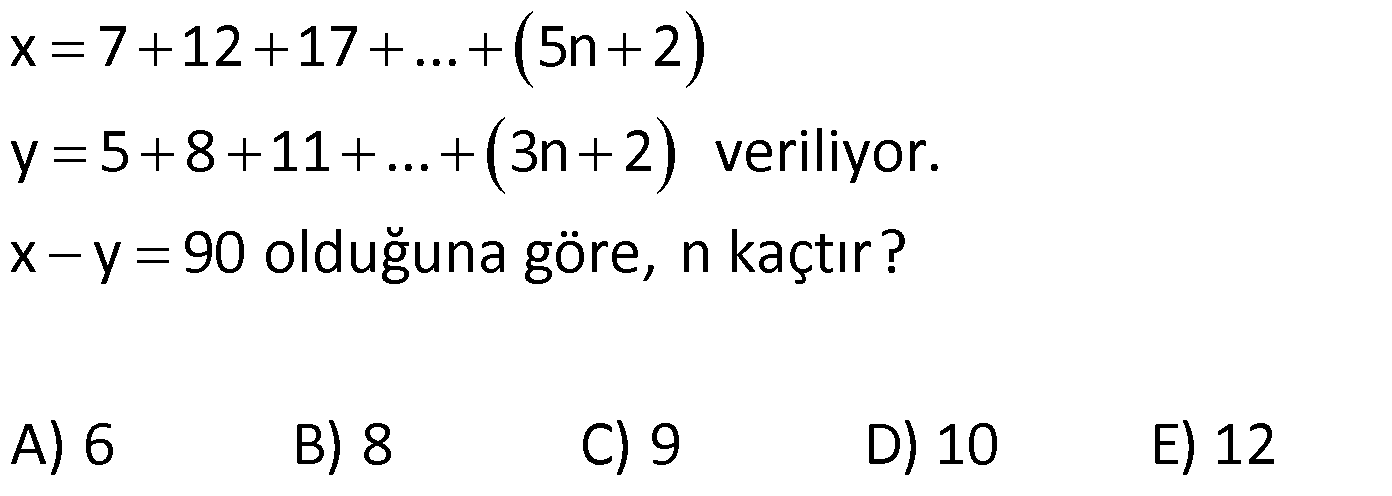

6.SORU


7.SORU


8.SORU
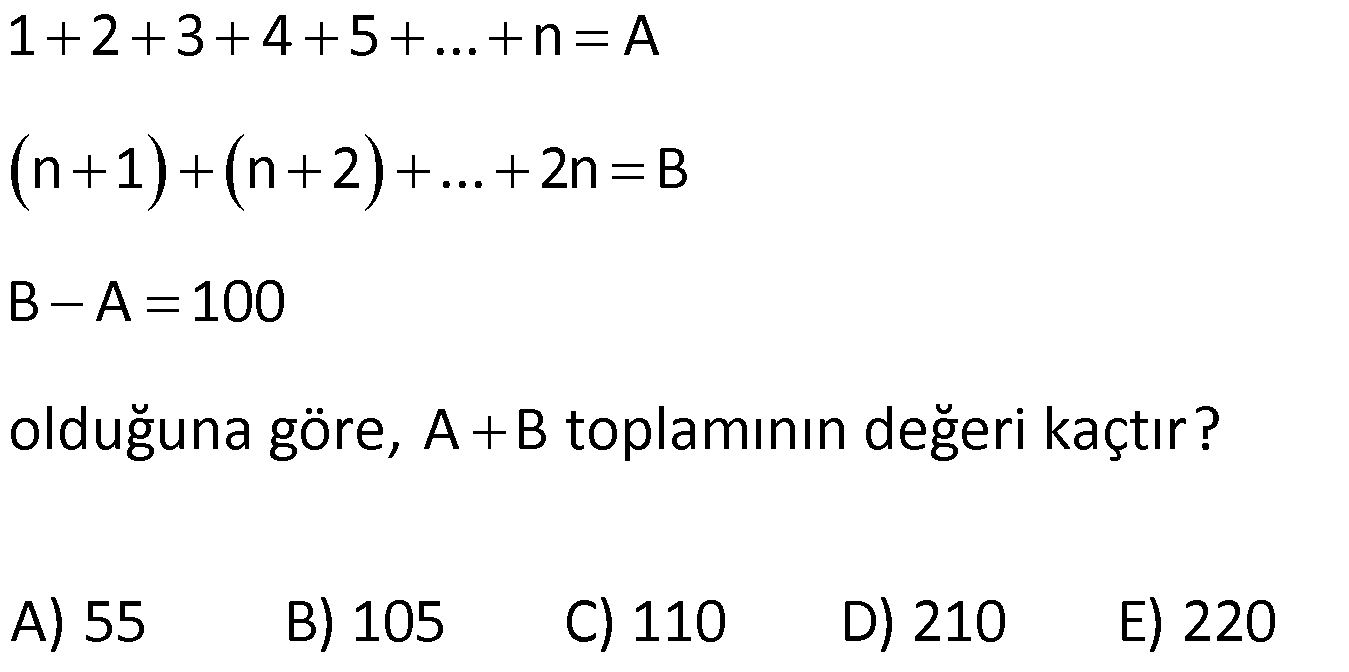

9.SORU

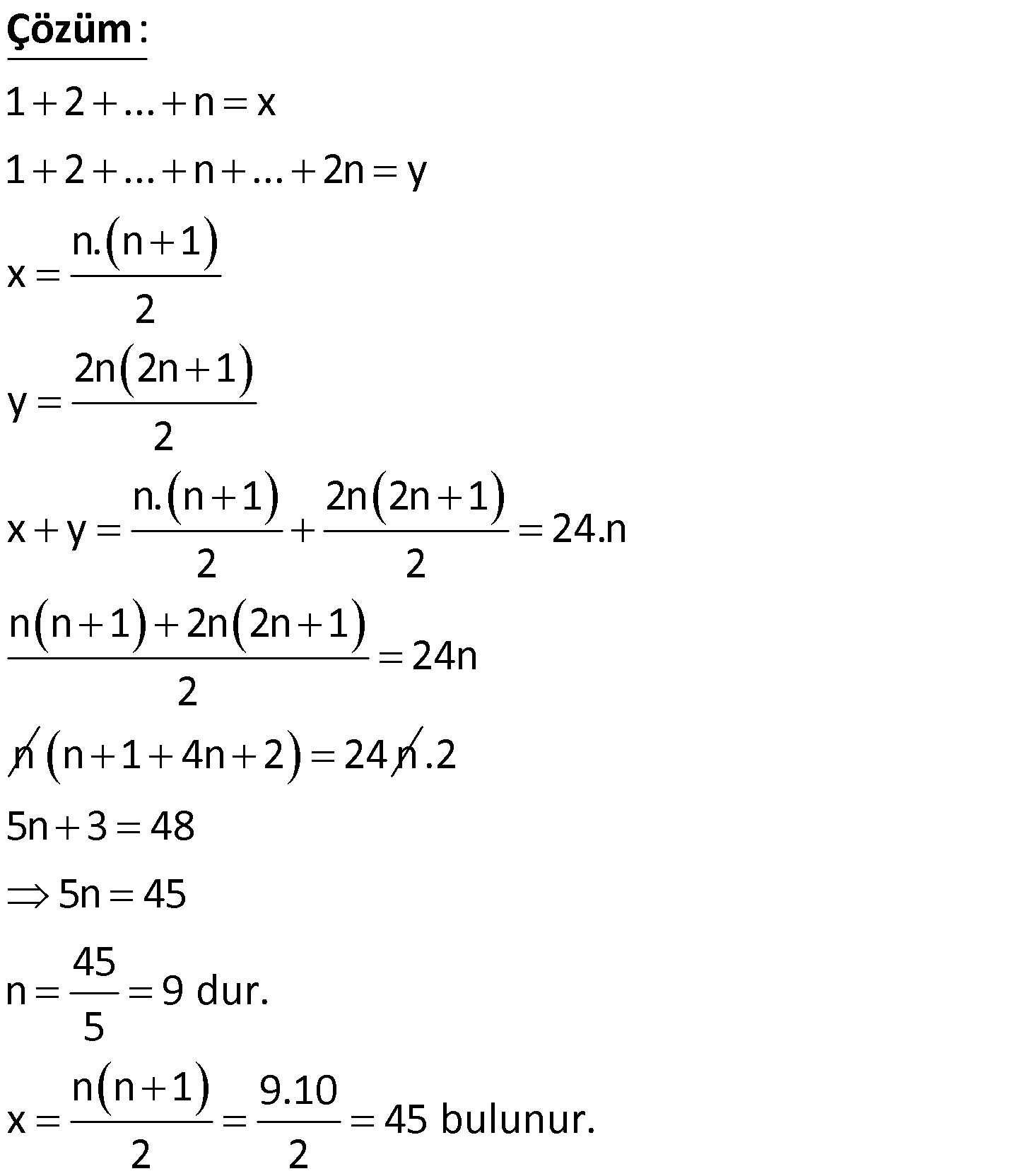
10.SORU
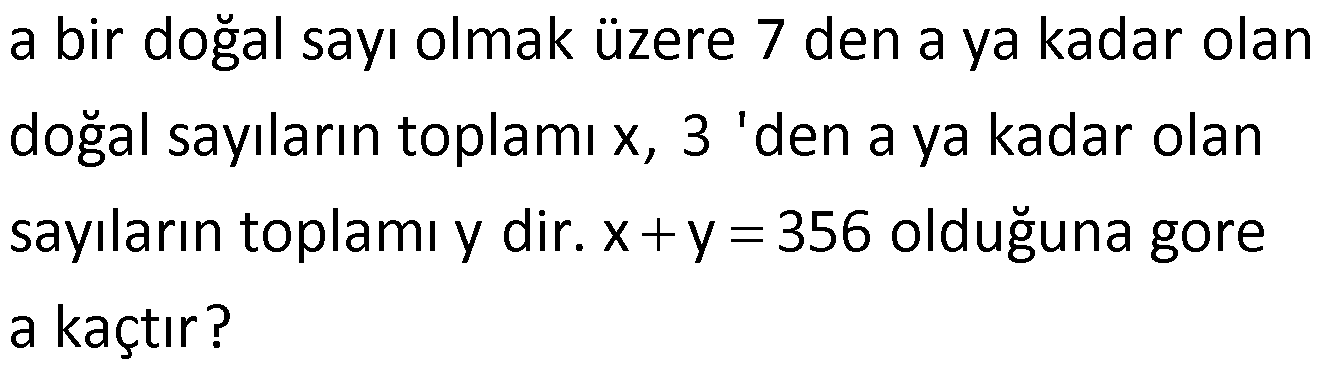
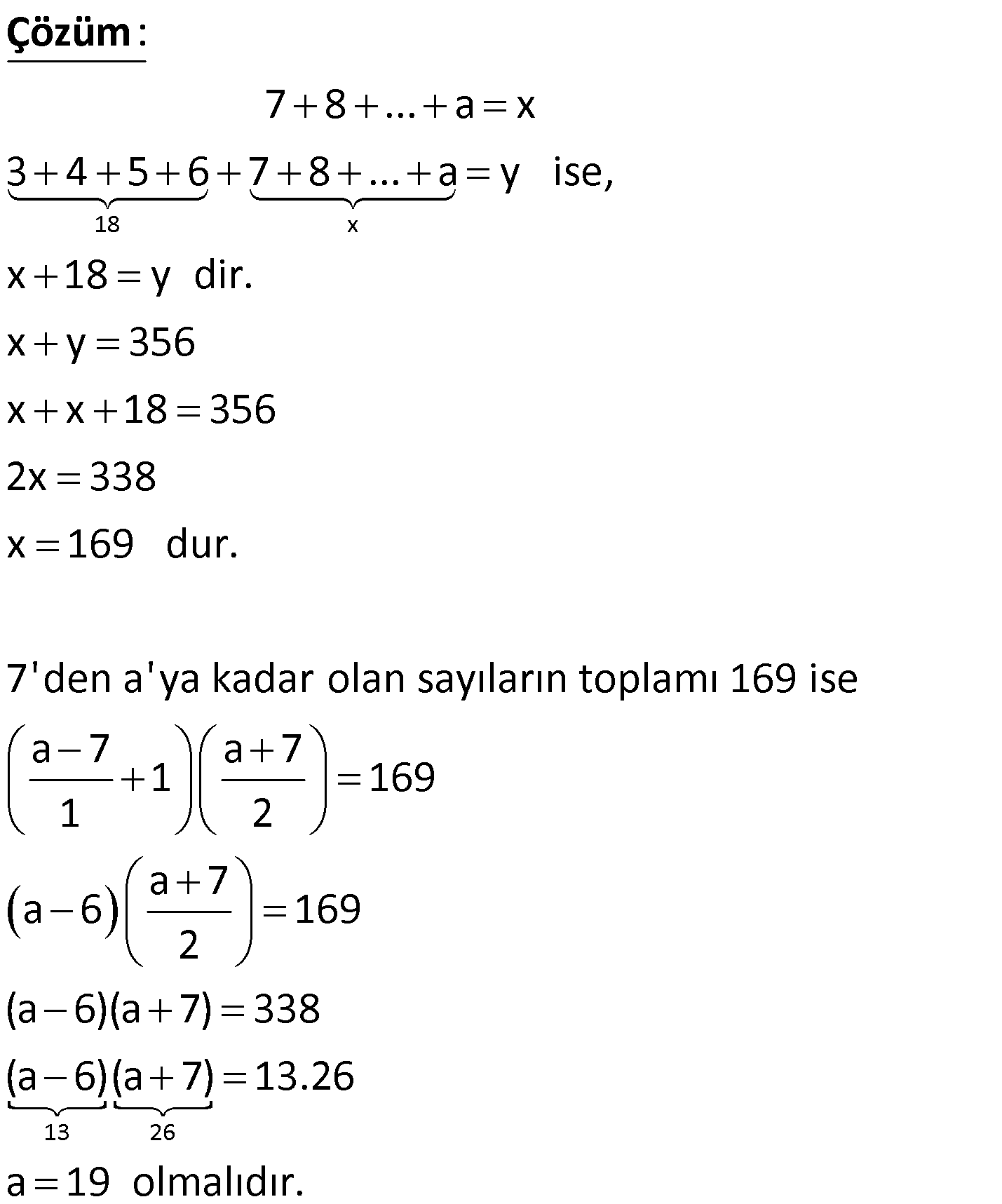
11.SORU

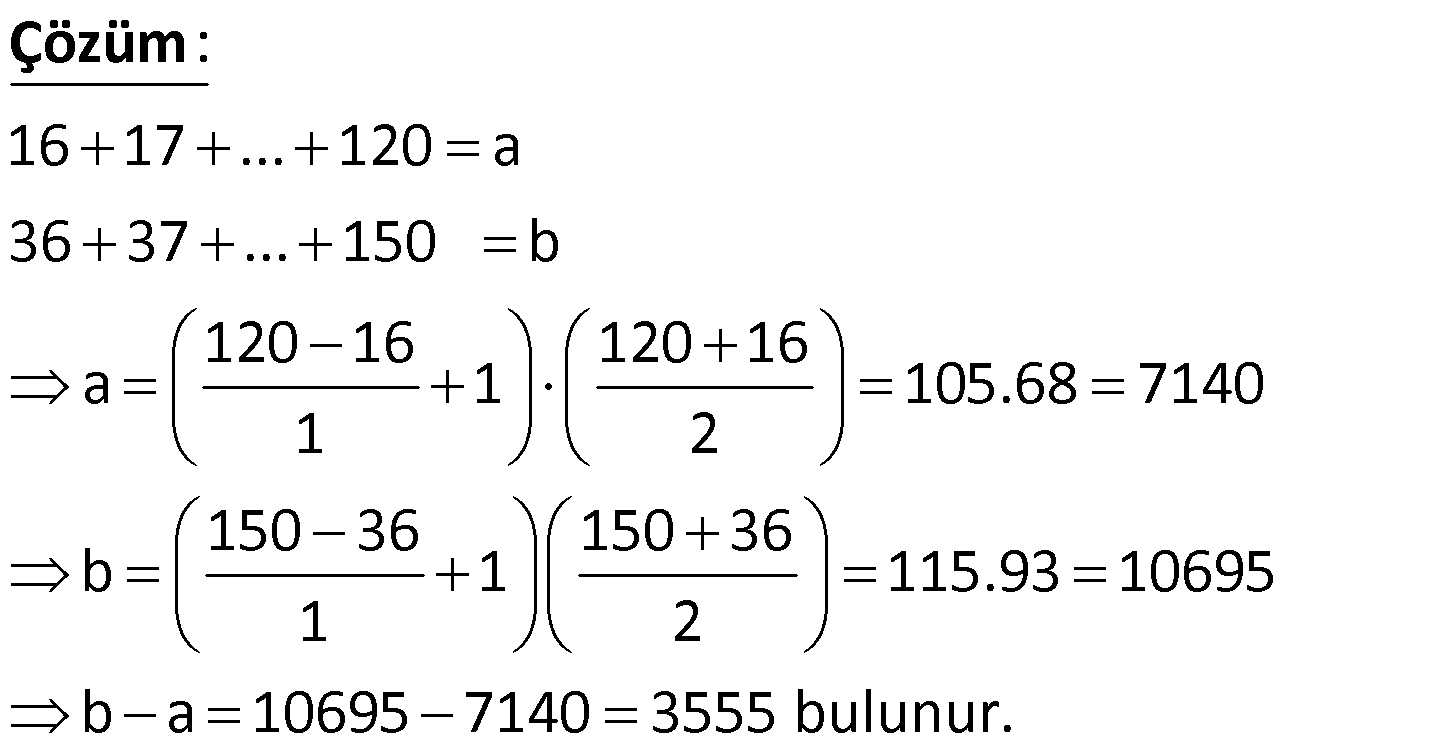
12.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
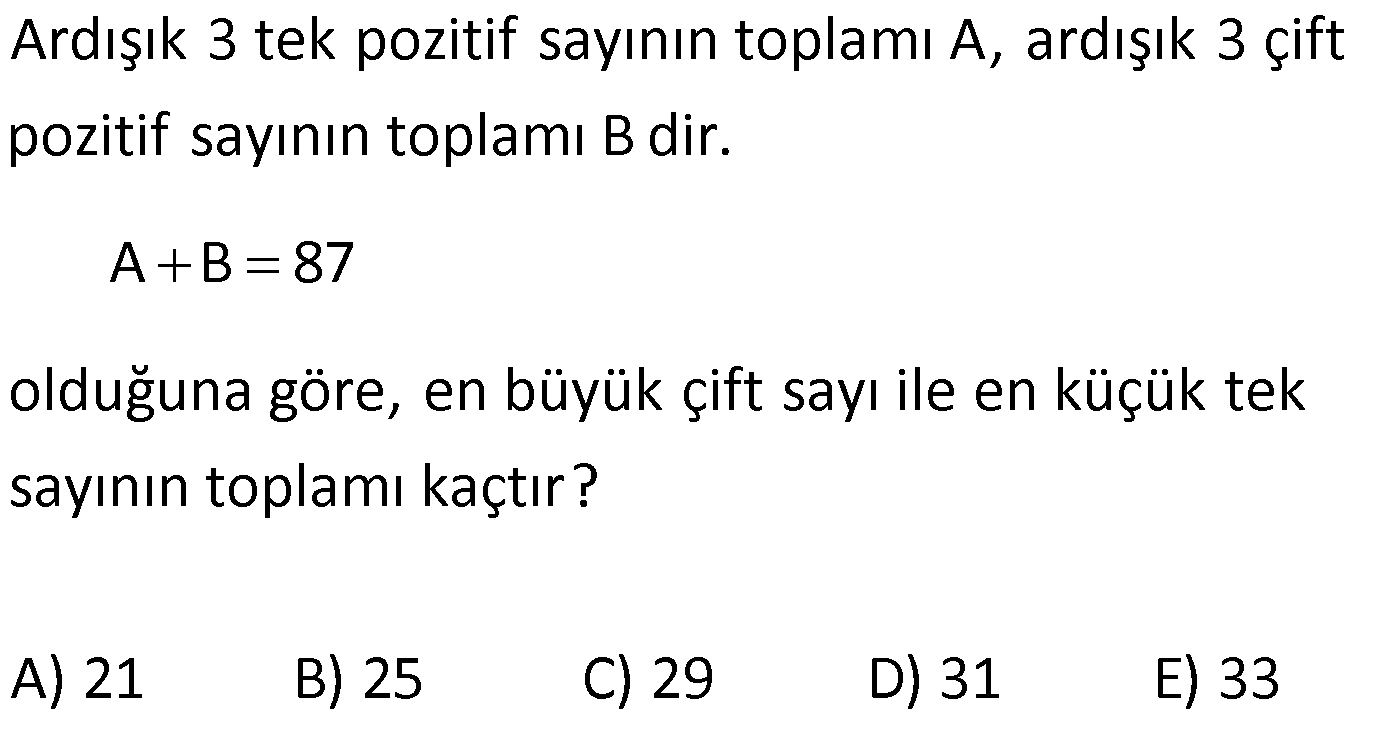
1 den n ye kadar doğal sayıların toplamı x, 4 ten n ye kadar doğal sayıların toplamı y dir. x y 104 olduğuna göre, x in değeri kaçtır ? www.matematikkolay.net : 1 2 3 4 … n x / 4 5 6 … n y 1 2 3 4 … n Çözüm x 4 5 6 … n y 1 2 3 x y 6 x y dir. x y 104 x y 6 2x 104 6 110 110 x 55 bulunur. 2 56 Ardışık 3 tek pozitif sayının toplamı A, ardışık 3 çift pozitif sayının toplamı B dir. A B 87 olduğuna göre, en büyük çift sayı ile en küçük tek sayının toplamı kaçtır? A) 21 B) 25 C) 29 D) 31 E) 33 www.matematikkolay.net Ardışık tek sayıl : ardan en küç üğü x olsun. Sayılar sır asıyla x,x 2,x 4 olur. A x x 2 x 4 3x 6 dır. Ardışık çif t Çözüm sayılardan en büyüğü y olsun. Sayılar sırasıyla y, y 2, y 4 olur. B y y 2 y 4 3y 6 dır. A B 87 3x 6 3y 6 87 3 x y 87 87 x y 29 bulunur. 3 58 Ardışık 5 çift sayı sırası ile K, L, M, N, T dir. K L M N T olduğuna göre, K T toplamı kaçtır? A) 20 B) 22 C) 24 D) 26 E) 28 www.matematikkolay.net Ardışık çift sayı : lar 2’şer a rtar.Sayıların hepsini K cinsinden yazalım. L K 2 M K 4 N K 6 T K 8 K L M N T K K 2 K Çözüm 4 K 6 K 8 3K 6 2K 14 3K 2K 14 6 K 8 dir. T K 8 8 8 16 dır. K T 8 16 24 bulunur. 59 x 7 12 17 … 5n 2 y 5 8 11 … 3n 2 veriliyor. x y 90 olduğuna göre, n kaçtır? A) 6 B) 8 C) 9 D) 10 E) 12 www.matematikkolay.net : x 7 12 17 … (5n 2) y 5 8 11 … (3n 2) taraf ta rafa çıkaralım. x y 2 4 6 … 2n Çözüm olur. x y 2(1 2 3 … n) dir. n.(n 1) x y 2 2 x y 2 n.(n 1) 2 9 10 90 n(n 1) n 9 olmalıdır. 62 n doğal sayı olmak üzere, 1 den n ye kadar olan doğal sayıların toplamı A, 10 dan n 1 e kadar olan doğal sayıların toplamı B dir. A B 120 olduğuna göre, n kaçtır? A) 50 B) 55 C) 60 D) 65 E) 75 www.matematikkolay.net : A 1 2 … 10 11 …. n 1 Çözüm n B 10 11 …. n 1 1 2 3 … 9 n 120 09.Eki n 120 2 45 n 120 n 120 45 75 bulunur. 63 x bir tek sayı olmak üzere; 2 den x e kadar olan çift sayıların toplamı A, 18 den x e kadar olan çift sayı – ların toplamı B ise, A B farkı kaçtır? A) 90 B) 72 C) 56 D) 42 E) 30 www.matematikkolay.net x bir tek sayı is : e, bunun 1 e ksiği son çift sayıdır. A 2 4 6 …16 18 20 22 …. x 1 B 18 20 22 … x 1 Çözüm taraf tarafa çıkaralım. 2 4 6 …16 18 20 22 …. x 1 _ 18 20 22… x 1 A B 2 4 6 … 16 Terim Sayısı . Sayıların Ortalaması 16 2 16 2 1 2 2 7 1 9 8.9 72 buluruz. 68 1 2 3 4 5 … n A n 1 n 2 … 2n B B A 100 olduğuna göre, A B toplamının değeri kaçtır? A) 55 B) 105 C) 110 D) 210 E) 220 www.matematikkolay.net : 1 2 3 … n A n 1 n 2 … 2.n B B A n 1 1 n 2 2 … 2n n 100 B A n 1 1 Çözüm n 2 2 n tane 2 … n 100 B A n n n… n 100 B A n.n 100 n 100 n 10 dur. A B 1 2 3 … n n 1 n 2 … 2.n A B 1 2 3 … 2.10 A B 1 2 3 … 20 20 A B 10 .21 2 210 bulunur. 69 1 den n ye kadar olan doğal sayıların toplamı x, 1 den 2n e kadar olan doğal sayıların toplamı y dir. x y 24.n olduğuna göre, x kaçtır? A) 45 B) 55 C) 66 D) 78 E) 91 www.matematikkolay.net : 1 2 … n x 1 2 … n … 2n y n. n 1 x 2 2n 2n 1 y 2 n. n 1 2n 2n 1 x y 24.n 2 2 n n 1 2n 2n 1 24n 2 n Çözüm n1 4n2 24 n .2 5n 3 48 5n 45 45 n 9 dur. 5 n n 1 9.10 x 45 bulunur. 2 2 82 a bir doğal sayı olmak üzere 7 den a ya kadar olan doğal sayıların toplamı x, 3 ‘den a ya kadar olan sayıların toplamı y dir. x y 356 olduğuna gore a kaçtır? www.matematikkolay.net 18 x : 7 8 … a x 3 4 5 6 7 8 … a y ise, x 18 y dir. x y 356 x x 18 356 2x Çözüm 13 26 338 x 169 dur. 7’den a’ya kadar olan sayıların toplamı 169 ise a 7 a 7 1 169 1 2 a 7 a 6 169 2 (a 6)(a 7) 338 (a 6)(a 7) 13.26 a 19 olmalıdır. 83 16 dan 120 ye kadar olan ve birer birer ar tan ardışık sayıların toplamı a, 36 dan 150 ye kadar olan ve birer birer ar tan ardışık sayıların toplamı b dir. Buna göre, b a farkı kaçtır? 16 17 … 120 : a 36 37 … 150 b 120 16 120 16 a 1 105.68 7140 1 2 150 36 150 36 b 1 1 2 Çözüm 115.93 10695 b a 10695 7140 3555 bulunur. www.matematikkolay.net 94 A 2.5 4.7 6.9 … 18.21 B 3.4 5.6 7.8 … 19.20 olduğuna göre, aşağıdakilerden hangisi doğrudur? A) A B 24 B) A B 1890 C) B A 18 D) A B 12 E) B A 26 www.matematikkolay.net 10 28 54 12 30 56 A 2.5 4.7 6.9 … 18.21 B 3.4 5.6 7.8 … 19.20 Dikkat edilirse, B’nin her terimi A’daki terimlerde : Çözüm n 2 fazladır. A ve B eşit sayıda terimden oluşuyor ve 18 2 terim sayıları 1 9 olarak buluruz. 2 (Az olduğu için terimler elle de sayılabilir.) B’nin 9 terimi de A’daki terimlerden 2’şer fazla olduğundan ; B A 9.2 B A 18 olarak ifade edebiliriz. 31

