Soru Sor sayfası kullanılarak Ardışık Sayılar konusu altında Ardışık Sayılarla ilgili denklem kurma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
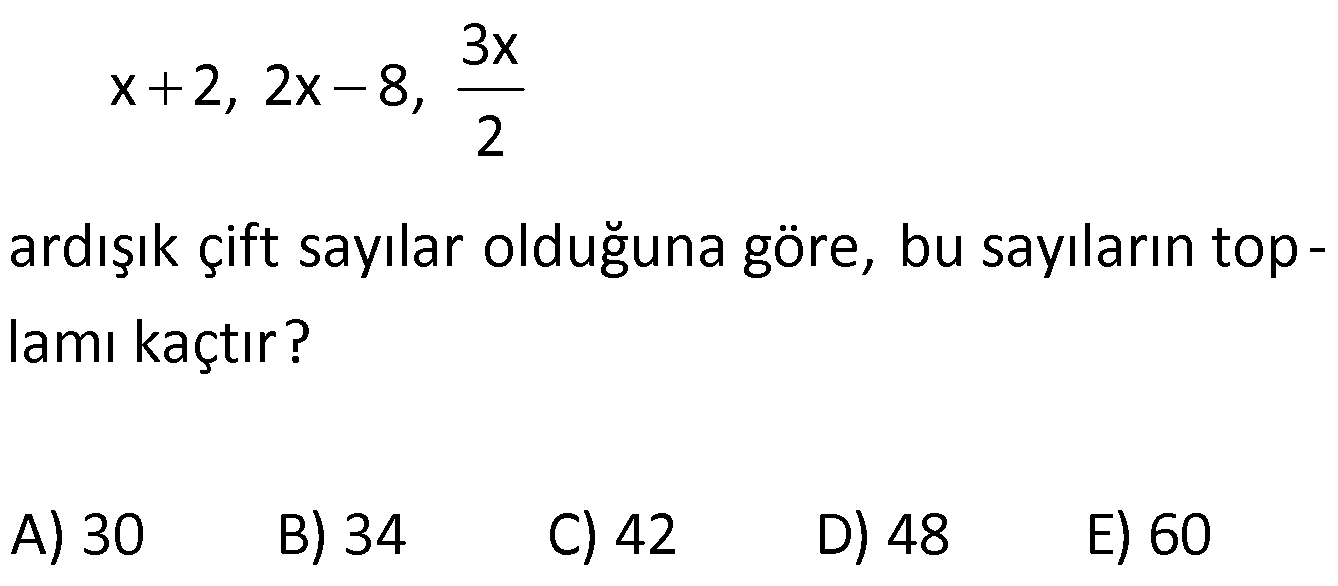

2.SORU

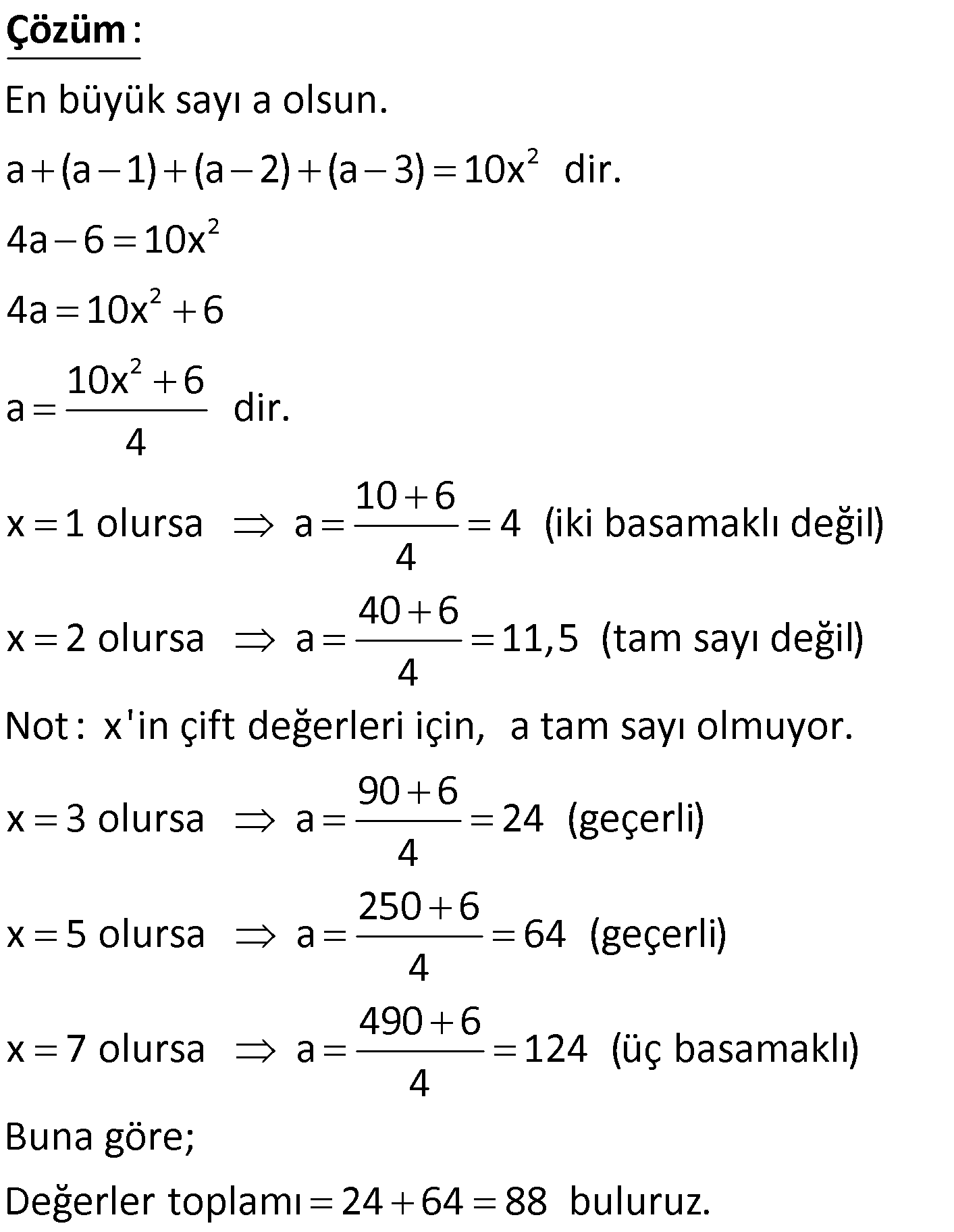
3.SORU


4.SORU

5.SORU


6.SORU


7.SORU


8.SORU

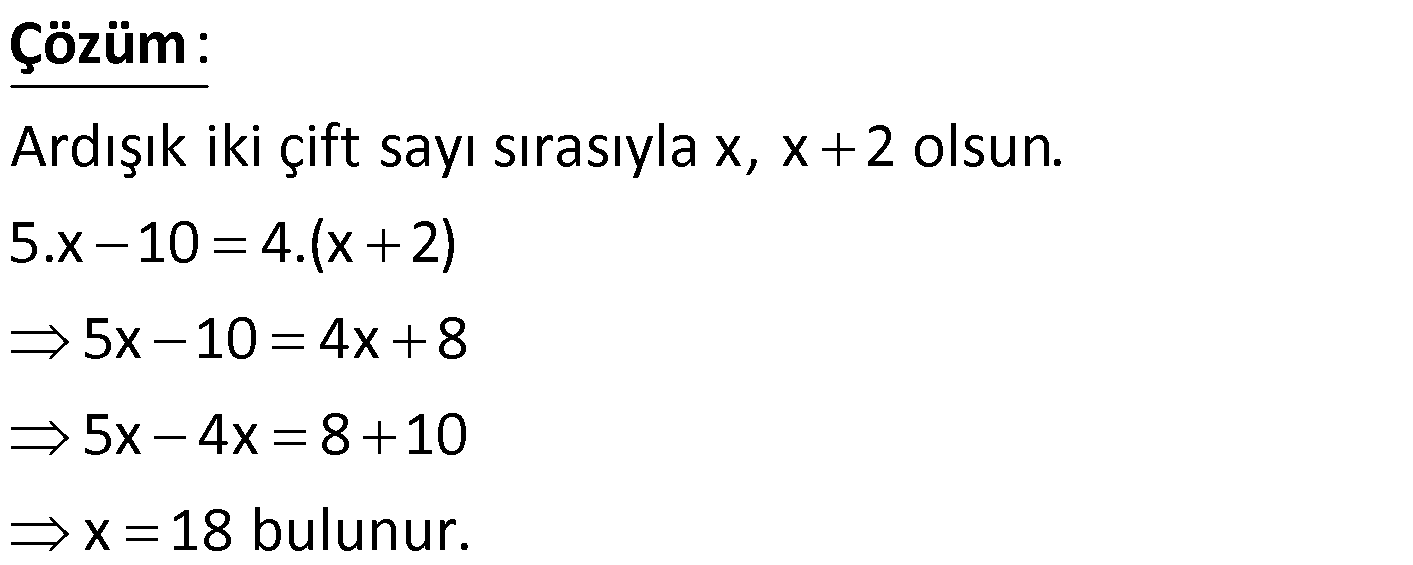
9.SORU

10.SORU


11.SORU

12.SORU


13.SORU


14.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
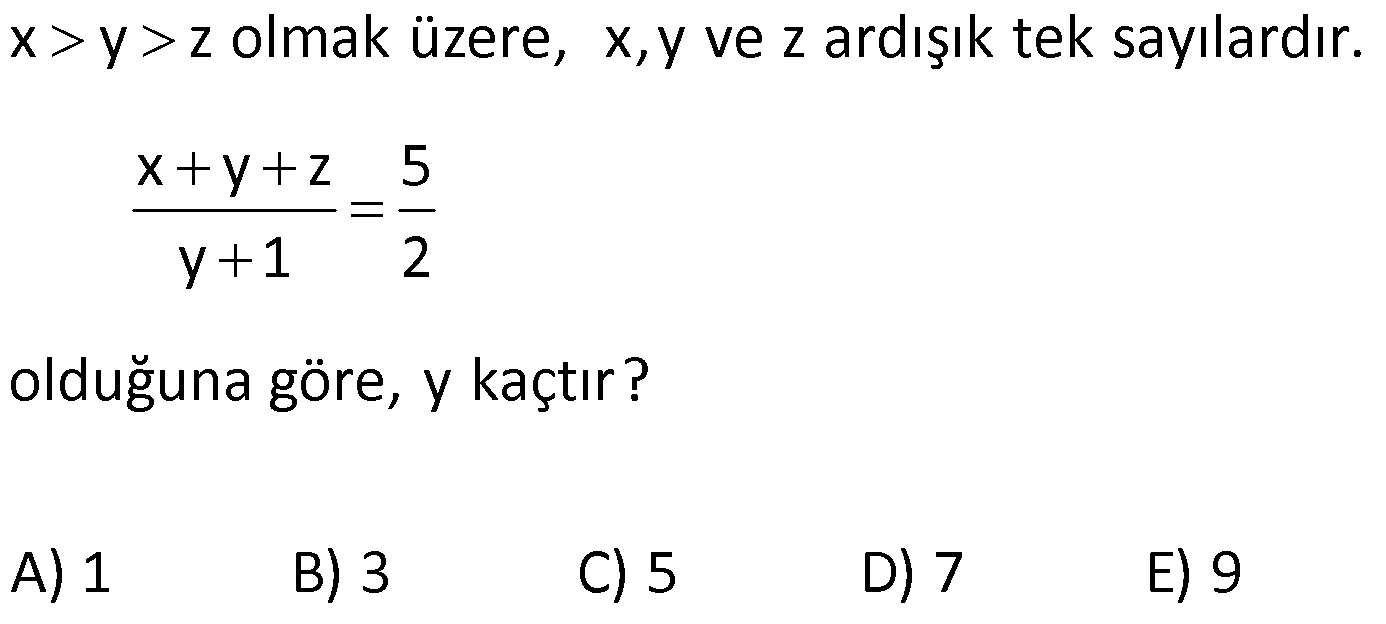
3x x 2, 2x 8, 2 ardışık çift sayılar olduğuna göre, bu sayıların top – lamı kaçtır? A) 30 B) 34 C) 42 D) 48 E) 60 www.matematikkolay.net Ardışık çift sayıla : r arasındaki f ark 2’dir. Buna göre; x 2 ile 2x 8 sayı arasında 2 fark var dır. 2x 8 (x 2) 2 x 2 Çözüm 8 x 2 2 x 10 2 x 12 dir. Buna göre; x 2 14 (en küçük sayı) diğerleri de 16 ve 18 olacaktır. Toplamları 14 16 18 48 buluruz. 14 İki basamaklı ardışık dört sayının toplamı bir tam sayının karesinin 10 katına eşittir. Bu dört sayıdan en büyüğünün alabileceği değerle – rin toplamı kaçtır? A) 84 B) 88 C) 92 D) 96 E) 98 www.matematikkolay.net 2 2 2 2 En büyük sayı a olsun. a : (a 1) (a 2) (a 3) 10x dir. 4a 6 10x 4a 10x 6 10x 6 a dir. 4 10 6 x 1 olursa a 4 4 Çözüm (iki basamaklı değil) 40 6 x 2 olursa a 11,5 (tam sayı değil) 4 Not : x’in çift değerleri için, a tam sayı olmuyor. 90 6 x 3 olursa a 24 (geçerli) 4 250 6 x 5 olursa a 64 (geçerli) 4 x 7 olursa 490 6 a 124 (üç basamaklı) 4 Buna göre; Değerler toplamı 24 64 88 buluruz. 15 Ardışık pozitif üç tek sayının çarpımı or tanca sayı – nın 621 katına eşit olduğuna göre bu üç sayının top – lamı kaçtır? A) 77 B) 75 C) 73 D) 71 E) 69 : Bu sayılar; a 2, a , a 2 olsun. (a 2).a.(a 2) 621a ise; ( . a 2) a Çözüm .(a2) 621 a 2 2 a 4 621 a 625 a 25 tir. Buna göre bu sayılar; 23,25 ve 27 dir. Toplamları 23 25 27 75 buluruz. 27 x y z olmak üzere, x,y ve z ardışık tek sayılardır. x y z 5 y 1 2 olduğuna göre, y kaçtır? A) 1 B) 3 C) 5 D) 7 E) 9 www.matematikkolay.net z k, y k 2, x k 4 olsun. Buna göre; x y z 5 k 4 k 2 k 5 y 1 2 k 2 1 2 3k 6 5 k 3 2 6k 12 5k 15 k 3 tür. O halde : Çözüm ; y k 2 32 5 buluruz. 28 n N, n tek sayı olmak üzere, 1’den n 1’e kadar olan tek sayıların toplamı a, 2 den n 2 ye kadar olan çift sayıların toplamı b olduğuna göre 1 den n’e kadar olan tam sayıların toplamı nedir? A) a b n B) a b 1 C) a b n 1 D) a b n 1 E) a b 1 1 3 5 7 .. l : ; . n 1 n 1 a ise; 1 3 5 7 … n 1 a (n 1) dir. 2 4 6 8 … n-2 b ise iki taraf a n ekleye i m. 2 Çözüm 4 6 8 … n 2 n b n olur. Bu iki eşitliği taraf tarafa toplarsak; 1 3 5 7 … n 1 a (n 1) 2 4 6 8 … n 2 n b n 1 2 3 4 ….. n a n 1b n ab 1 buluruz. www.matematikkolay.net 33 Ardışık pozitif üç sayının çarpımı, en büyük sayının 42 katına eşittir. Buna göre, bu sayıların toplamı kaçtır? A) 21 B) 24 C) 27 D) 28 E) 32 : ) Sayılara sırasıyla; x,x 1,x 2 olsun. x.(x 1). ( x 2 Çözüm 42. (x 2) x.(x 1) 42 x 6 olur. Sayılar; 6,7,8 dir. 6 7 8 21 bulunur. www.matematikkolay.net 35 Ardışık üç çift tam sayının çarpımı or tanca sayının 140 katına eşit olduğuna göre, bu sayıların toplamı kaçtır? A) 30 B) 36 C) 42 D) 48 E) 54 www.matematikkolay.net : a Bu sayı a ; 2 l r a , a ve a 2 olsun. (a 2). Çözüm .(a2) 140. a 2 2 ise a 4 140 a 144 a 12 dir. Buna göre; bu sayılar 10, 12 ve 14 tür. Toplamları 10 12 14 36 buluruz. 39 Ardışık iki pozitif çift tamsayının küçüğünün 5 katı – nın 10 eksiği, büyüğünün 4 katına eşit ise bu sayı – lardan küçük olanı kaçtır? : Ardışık iki çift sayı sırasıyla x, x 2 olsun. 5.x 10 4.(x 2) 5x 10 4x 8 5x 4x 8 10 x 18 bulunur. Çözüm 40 En büyüğü A olan B tane ardışık tam sayının toplamı 10B olduğuna göre, A B aşağıdakilerden hangisine eşit olabilir? B 10 10 B 3B 10 A) B) C) 2 2 2 3B 19 19 3B D) E) 2 2 www.matematikkolay.net B tane ardışık sa : yıdan B. ola n A ise 1.si; A B 1 dir . Ardışık sayıların toplamı İlk terim Son ter Terim sayı s ı Çözüm im 2 B .(A B 1 A) 10B 2 2A B 1 20 2A B 19 Her tarafa 3B ekleyelim. 2A B 3B 19 3B 2A 2B 3B 19 3B 19 A B bulunur. 2 42 Ardışık iki tek sayıdan küçüğünün 2 katı ile büyüğü – nün 3 katının toplamı aşağıdakilerden hangisi olabilir? A) 73 B) 74 C) 75 E) 76 D) 77 www.matematikkolay.net Ardışık tek sayıl : ardan küçüğü n olsun.Büyüğü n 2 olsu n. Küçüğünün 2 katı 2.n Büyüğünün 3 katı 3.(n 2) 3n 6 İk isi Çözüm 5k nin toplamı 3n 6 2n 5n 6 5n 5 1 Sayı 5’in katından 1 fazla olmalı. Buna göre 76 olabilir. 44 n tane iki basamaklı farklı doğal sayısının toplamı 51.n olduğuna göre n en fazla kaç olabilir? A) 28 B) 49 C) 80 D) 83 E) 86 www.matematikkolay.net En büyük sayı : 10 11 12 … 10 n 1 51n 10 10 1 10 2 … 10 n 1 51n n tane 10 1 2 3 … n 1 51n (n 1 1 0n Çözüm ).n 51n 2 n n 1 (10 ) 51n 2 n 1 10 51 2 20 n 1 102 n 102 20 1 n 83 buluruz. 51 a b c olmak üzere a, b ve c ardışık üç doğal sayı – dır. a.b çarpımı c ile bölündüğünde bölüm ile kalanın toplamı 14 olmaktadır. Buna göre, a kaçtır? A) 16 B) 15 C) 14 D) 13 E) 12 www.matematikkolay.net 2 2 2 a b c ise b ve c’y : i a cinsinden yazalım. b a 1, c a 2 olu r. a.b a. a 1 a a a a a 2 a 2a a 1 Çözüm a a 2 2 Bölüm a 1 Kalan 2 a 1 2 14 a 1 14 a 13 bulunur. 70 3 ün katı olan ardışık üç pozitif çift tam sayının çar – pımları, toplamlarının 180 katına eşittir. Buna göre, bu sayıların en büyüğü kaçtır? A) 12 B) 18 C) 24 D) 30 E) 36 www.matematikkolay.net 3’ün katı ardışık : çift sayıla rın arasında 6 fark var d ır. En büyük sayı x olsun. Or tanca sayı x 6 Küçük sayı x 1 Çözüm 2 olur. Çarpımları 180.(Toplamları) ise, x.(x 6).(x 12) 180.(x x 6 x 12) x.(x 6).(x 12) 180.(3x 18) x. (x 6) .(x 12) 180.3. (x 6) 30 18 x.(x 12) 18.10.3 x .(x 12) 18.30 x 30 olmalıdır. 84 1 13 a b c 3 2 sıralamasında birbirini izleyen sayılar arasındaki farklar eşittir. Buna göre, c a farkı kaçtır? 37 37 37 37 37 A) B) C) D) E) 24 12 6 3 2 a b c 13/2 Ardışık sayılar arasında : ki fark k ols un. 1 13 a b c sıralamasını 3 2 1 1 1 1 1 k 2k 3k 4k olar ak 3 3 3 3 3 Çözüm 3 2 yazabiliriz. 1 13 4k ise; 3 2 13 1 39 2 4k 2 3 6 37 37 4k k tür. O halde; 6 24 37 37 c a 2k 2 buluruz. 24 12 www.matematikkolay.net 99

