Soru Sor sayfası kullanılarak 2.Dereceden Denklemler konusu altında Rasyonel katsayılı denklem ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

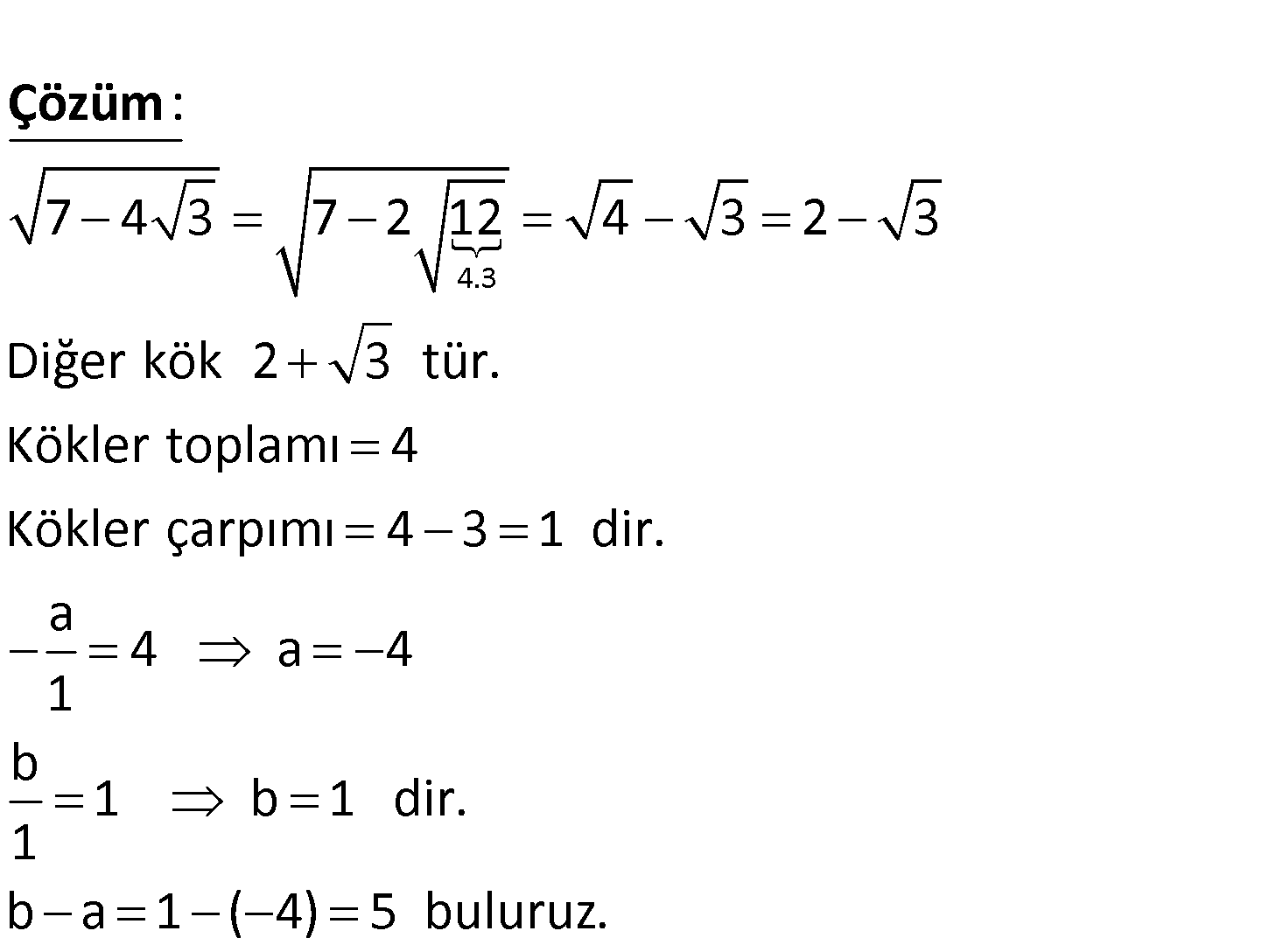
3.SORU


4.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
Köklerinden biri 1 2 olan rasyonel katsayılı ikin – ci dereceden denklem aşağıdakilerden hangisi ola 2 2 2 2 2 – bilir? A) x 2x 1 B) x x 2 0 C) x x 2 D) x 2x 1 0 E) x 4x 1 0 Köklerden biri 1 2 ise; diğeri 1 2 dir. Kökler toplamı 2 Kökler çarpımı 1 2 1 dir. Bun : a g Çözüm 2 öre denklemi; x 2x 1 0 şeklinde yazabiliriz. www.matematikkolay.net 53
2 a ve b iki tamsayıdır. x ax b 0 denkleminin bir kökü 7 4 3 olduğuna göre, b a farkı kaçtır? A) 6 B) 5 C) 4 D) 3 E) 2 04.Mar 7 4 3 7 2 12 4 3 2 3 Diğer kök 2 3 tür. Kökler toplamı 4 Kökler çarpımı 4 3 1 dir. a 4 : 1 Çözüm a 4 b 1 b 1 dir. 1 b a 1 ( 4) 5 buluruz. www.matematikkolay.net 59
2 2x m 1 x 4n 0 rasyonel katsayılı denkleminin köklerinden biri 3 5 olduğuna göre, m n top lamı kaçtır? A) 11 B) 12 C) 13 D) 14 E) 15 www.matematikkolay.net Katsayılar rasyonel olduğunda Köklerden biri 3 5 ise diğer kök bunun eşleniği yani 3 5 m : ol Çözüm alıdır. O halde kökler toplamı; 3 5 3 5 6 dır. b m 1 m 1 Kökler toplamı dir. a 2 2 m 1 Eşitleyelim. 6 m 11 dir. 2 Kökler çarpımı; 3 5 3 5 9 5 4 tür. c 4n Kökler çarpımı 2n dir. a 2 Eşitleyelim. 2n 4 n 2 dir. m n 11 2 13 buluruz. 99
4 2 4 2 5 3 sayısı, aşağıdaki denklemlerden hangisinin bir köküdür? A) x 8x 4 0 B) x 8x 4 0 4 2 4 2 4 2 C) x 16x 4 0 D) x 16x 4 0 E) x 12x 8 0 www.matematikkolay.net 2 2 y x olsun. x 5 3 ise x 5 2 15 3 8 2 15 tir. O halde y 8 2 15 tir. 2.dereceden denklemin : Çözüm 1 2 2 Kökl bir kökü y 8 2 15 ise diğer kökü bunun eşleniğidir. y 8 2 15 tir. Kökler toplamı 8 2 15 8 2 15 16 dır. Kökler çarpımı 8 2 15 8 2 15 64 60 4 tür. O halde bu denklem y 16 er Kökler toplamı Çarpımı 2 4 2 y 4 0 dır. y yerine x yazdığımızda; x 16x 4 0 buluruz. 105

