Soru Sor sayfası kullanılarak 2.Dereceden Denklemler konusu altında Kökler sıralanarak verilmişse ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

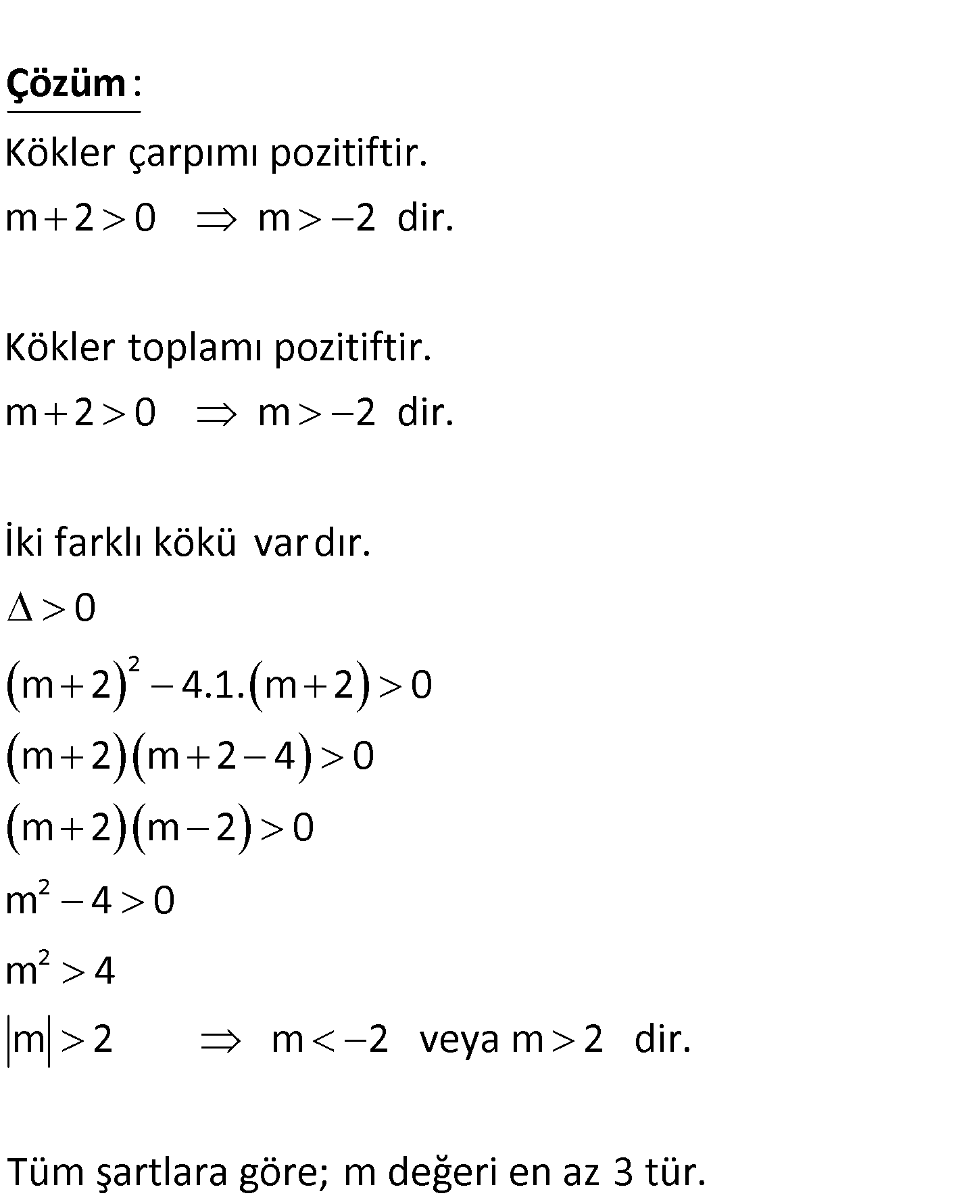
2.SORU


3.SORU
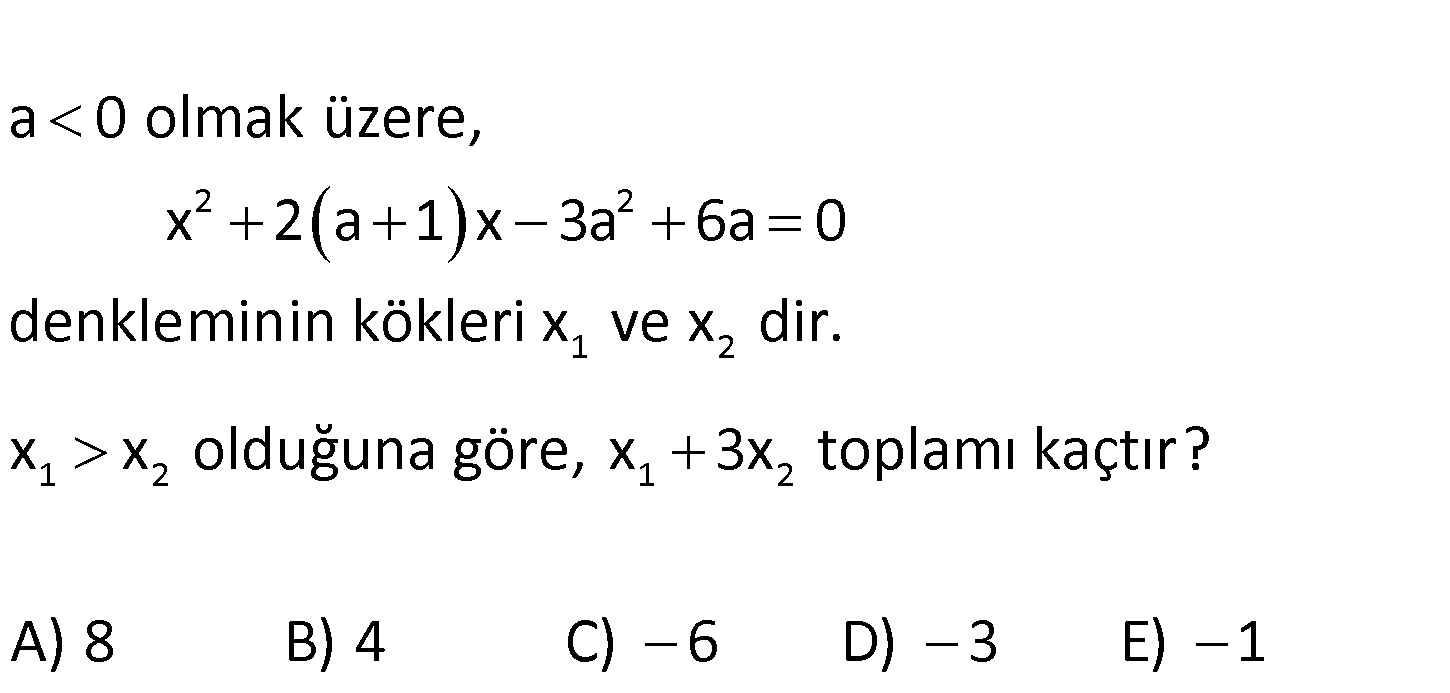
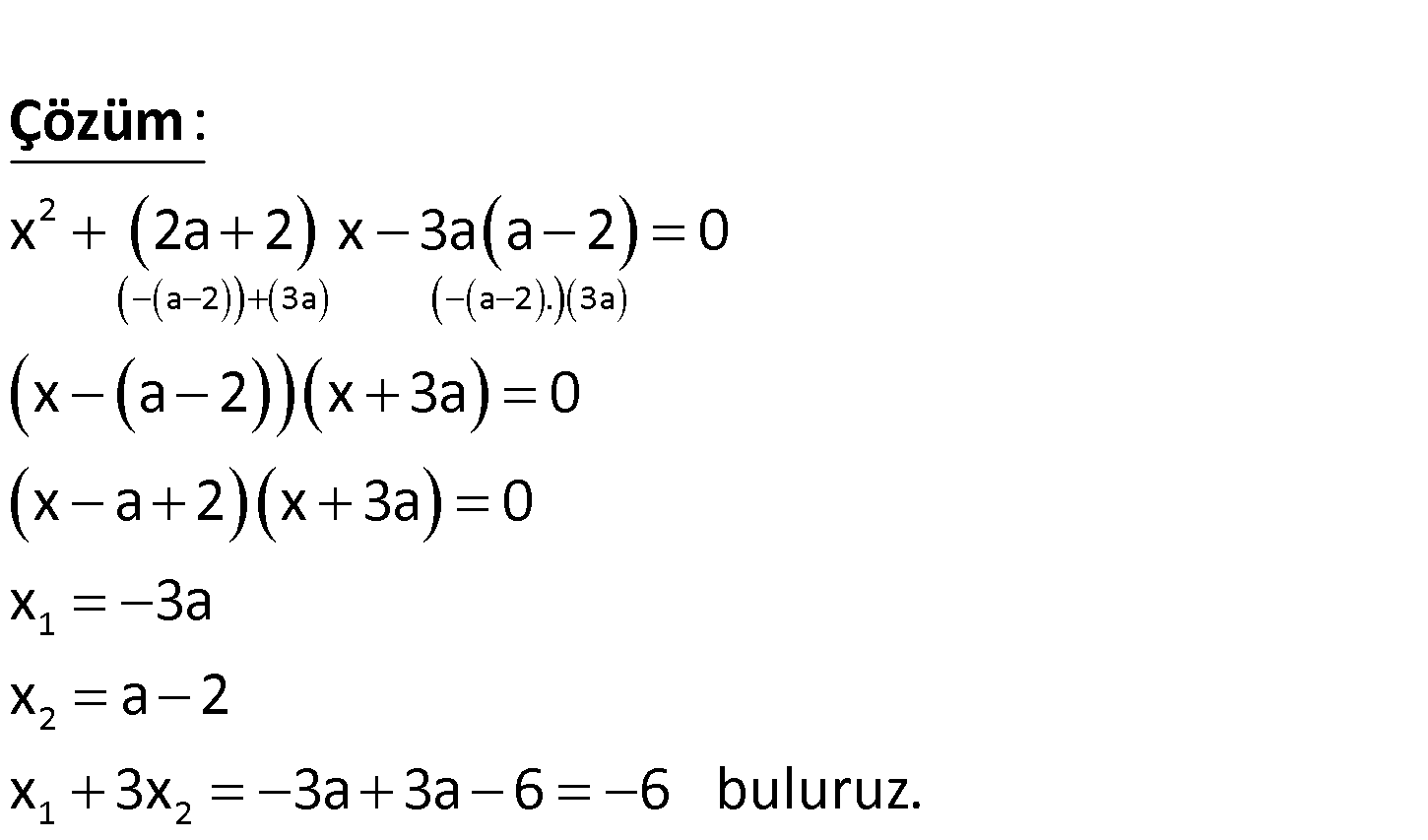
4.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 1 2 1 2 x m 2 x m 2 0 denkleminin x ve x kökleri arasında 0 x x sıralaması var sa m nin alabilec eği en küçük tam sayı değeri kaçtır? A) 3 B) 1 C) 0 D) 1 E) 3 www.matematikkolay.net Kökler çarpımı pozitiftir. m 2 0 m 2 dir. Kökler toplamı pozitiftir. m 2 0 m 2 dir. : Çözüm 2 2 2 İki farklı kökü var dır. 0 m 2 4.1. m 2 0 m 2 m 2 4 0 m 2 m 2 0 m 4 0 m 4 m 2 m 2 veya m 2 dir. Tüm şartlara göre; m değeri en az 3 tür. 111
www.matematikkolay.net 2 1 2 1 2 2x 5x m 1 0 denkleminin kökleri x ve x dir. x x 0 olması için, m nin alabileceği değerler kümes i aşağıdakilerden hangisidir? 33 A) 1, B) 1, C) , 1 8 33 D) 0, 1 E) , 8 Köklerin ikisi de negatif olduğundan, kökler çarpımı pozitif olmalıdır. m 1 Kökler çarpımı: : 0 2 Çözüm 2 m 1 dir. Ayrıca iki farklı kök bulunduğundan, 0 dır. 5 4.2.(m 1) 0 25 8(m 1) 0 25 8m 8 0 33 8m 33 m dir. 8 33 m’in değerler kümesi: 1, buluruz. 8 38
2 2 1 2 1 2 a 0 olmak üzere, x 2 a 1 x 3a 6a 0 denkleminin kökleri x ve x dir. x x olduğuna göre, 1 2 x 3x toplamı kaçtır? A) 8 B) 4 C) 6 D) 3 E) 1 2 a 2 3a a 2 . 3a 1 2 1 2 x 2a 2 x 3a a 2 0 x a 2 x 3a 0 x a 2 x 3a 0 x 3a x a 2 x 3x 3a 3a 6 6 buluruz : Çözüm . 95
3 2 1 2 3 f x x ax bx 3 fonksiyonunun grafiği A 2, 1 ve B 1, 2 noktalarından geçip x eksenini x , x , x 1 2 3 1 2 3 1 2 2 3 apsisli noktalarda kesiyor. x x x olduğuna göre, aşağıdakilerden hangisi yanlıştır? A) x 0 B) x 1 C) 1 x D) x .x <0 E) x .x 0 www.matematikkolay.net 3 2 B(1, 2) x ax bx 3 2 1 a b 3 2 : Çözüm 3 2 a b 6 dır. A( 2,1) x ax bx 3 2 8 4a 2b 3 1 4a 2b 6 dır. a b 6 4a 2b 6 5a b 0 5a b a 1 ve b 5 bulur 3 2 1 2 3 3 3 1 2 3 1 uz. f(x) x x 5x 3 x x x 1 Mutlaka biri pozitif olmalıdır. en büyükleri x ise x pozitiftir. x .x .x 3 Ya biri negatiftir, ya da üçü. Ancak biri pozitif olmak zorunda olduğundan sadece x n 2 egatif olabilir. Bu sebeple x pozitiftir. E şıkkındaki ifade de bu nedenle yanlıştır. 48

