Soru Sor sayfası kullanılarak 2.Dereceden Denklemler konusu altında Kökler arasındaki bağıntı ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
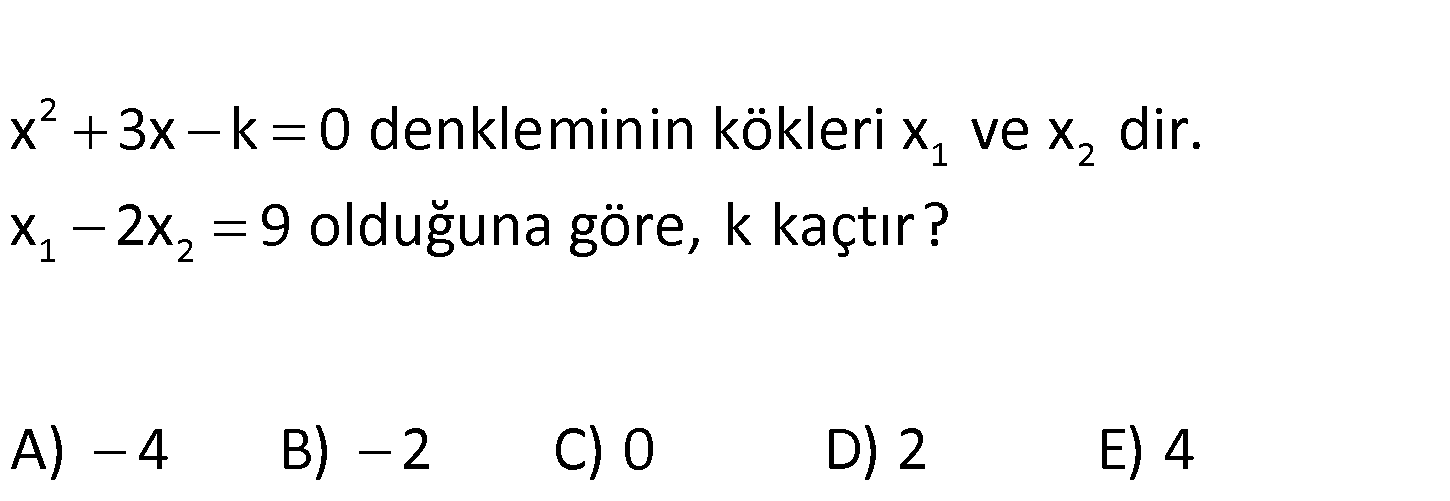

3.SORU

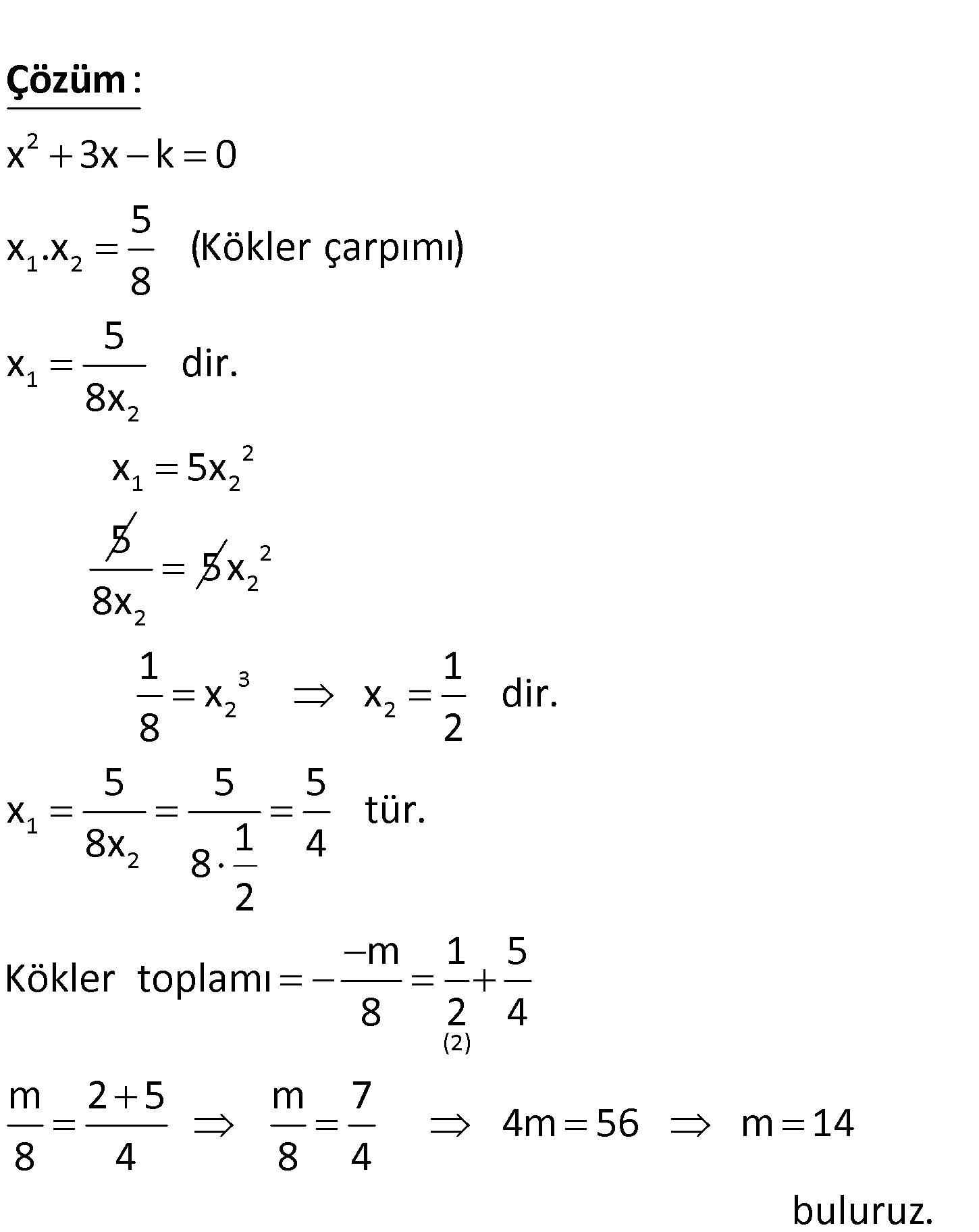
4.SORU

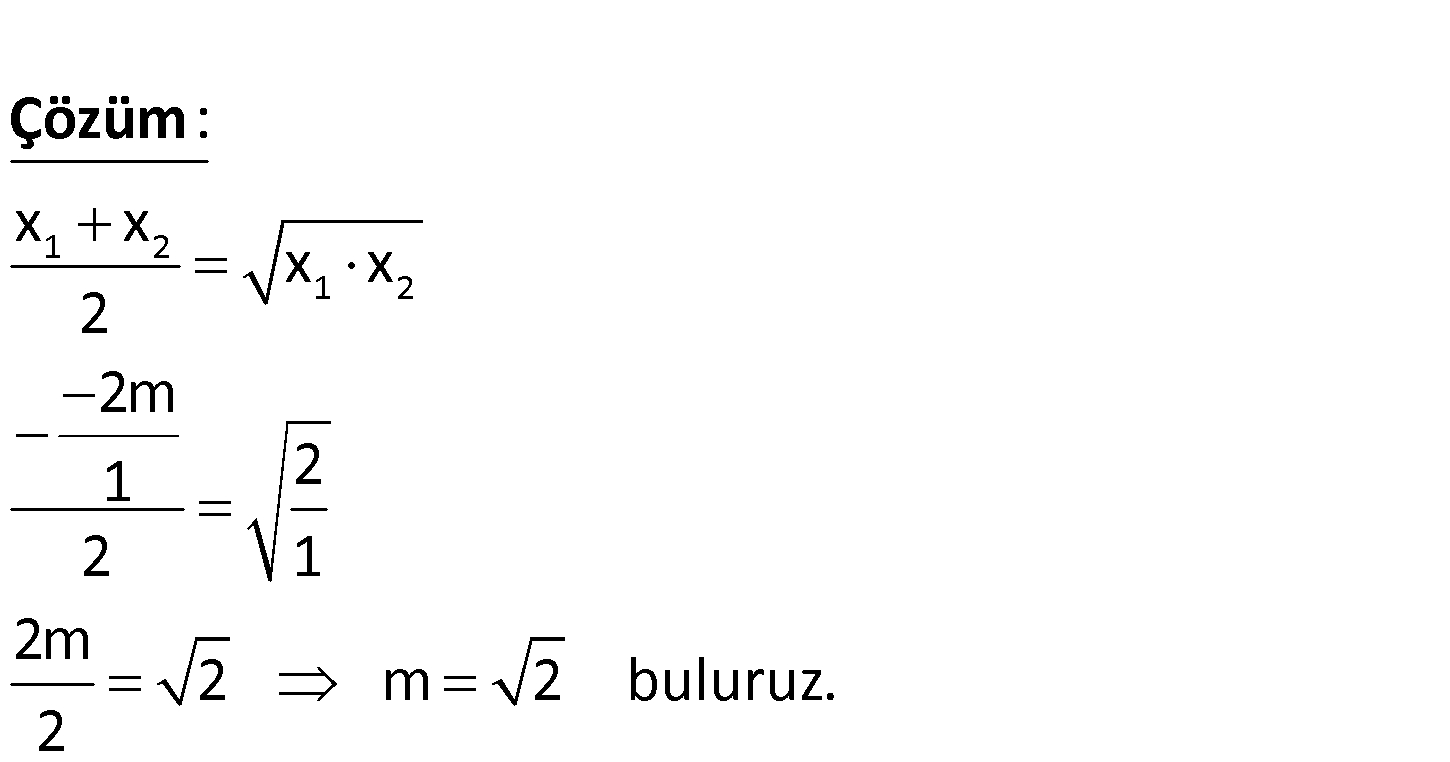
5.SORU

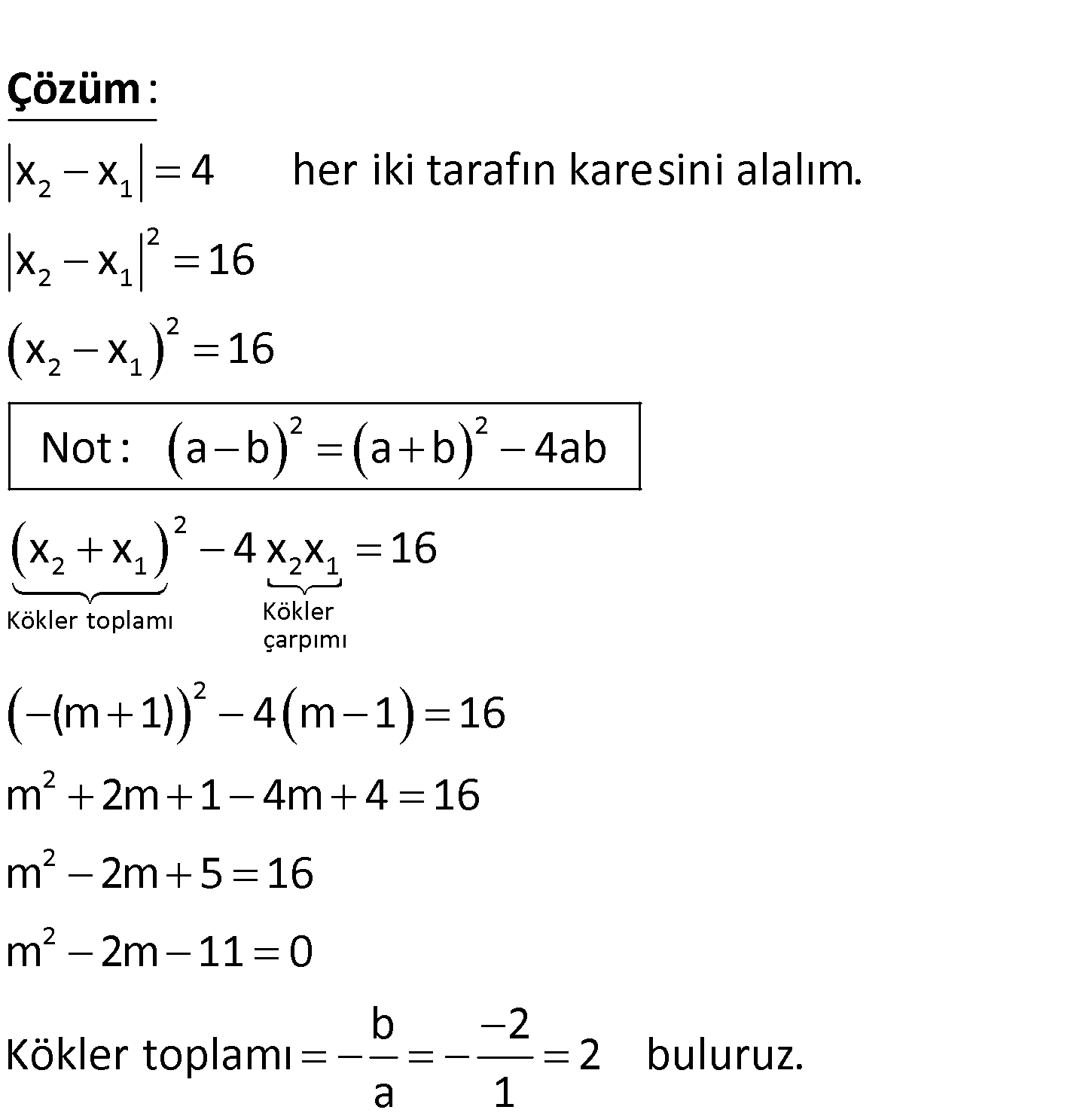
6.SORU


7.SORU


8.SORU


9.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 1 2 1 2 x 6x n 0 denkleminin kökleri x ve x dir. x 3x 14 olduğuna göre, n kaçtır? A) 16 B) 12 C) 4 D) 1 E) 5 www.matematikkolay.net 2 1 2 1 2 1 2 x 6x n 0 denkleminde 6 kökler toplamı x x 6 dır. 1 x 3x 14 – / x x 6 : Çözüm 2 2 2 2 2 4x 8 x 2 dir. x 2 değerini denklemde yerine yazalım. x 6x n 0 ( 2) 6 ( 2) n 0 4 12 n 0 n 16 buluruz. 19
2 1 2 1 2 x 3x k 0 denkleminin kökleri x ve x dir. x 2x 9 olduğuna göre, k kaçtır? A) 4 B) 2 C) 0 D) 2 E) 4 2 1 2 1 2 1 2 2 2 x 3x k 0 3 x x 3 (Kökler toplamı) 1 x 3 x x 2x 9 ( 3 x ) 2x 9 : Çözüm 2 2 2 2 2 3 3x 9 3x 12 x 4 tür. 4, denklemi sağlayacaktır. Buna göre; x 3x k 0 ( 4) 3.( 4) k 0 16 12 k 0 k 4 buluruz. www.matematikkolay.net 34
2 1 2 2 1 2 8x mx 5 0 denkleminin kökleri x ve x dir. x 5 x olduğuna göre m kaçtır? A) 16 B) 14 C) 12 D) 10 E) 8 2 1 2 1 2 2 1 2 x 3x k 0 5 x .x (Kökler çarpımı) 8 5 x dir. 8x x 5x 5 : Çözüm 2 5 8x 2 2 3 2 2 1 2 -2 x 1 1 x x dir. 8 2 5 5 5 x tür. 8x 1 4 8 2 m 1 5 Kökler toplamı 8 2 4 m 2 5 m 7 4m 56 m 14 8 4 8 4 buluruz. 35
2 x 2mx 2 0 denkleminin köklerinin aritmetik ortalaması geometrik ortalamasına eşit ise m kaç – tır? 1 2 1 2 x x x x 2 2m 1 2 2 1 2m 2 m 2 buluruz. 2 : Çözüm 50
2 1 2 2 1 x m 1 x m 1 0 denkleminin x ve x kökle – ri arasında x x 4 bağıntısı var sa m nin alabile – ceği d eğerler toplamı kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 www.matematikkolay.net 2 1 2 2 1 2 2 1 2 2 2 1 x x 4 her iki tarafın karesini alalım. x x 16 x x 16 Not : a b a b 4ab x x : Çözüm 2 2 1 Kökler toplamı Kökler çarpımı 2 2 2 2 4 x x 16 (m 1) 4 m 1 16 m 2m 1 4m 4 16 m 2m 5 16 m 2m 11 0 b 2 Kökler toplamı 2 buluruz. a 1 93
2 1 2 1 2 x ax a 1 0 denkleminin kökleri olan x ve x arasında 2x x 7 bağıntısı olduğuna göre, a kaç olabilir? A) 4 B) 6 C) 3 D) 5 E) 8 www.matematikkolay.net 2 1 2 1 1 2 a 1 2 x ax a 1 0 2x x 7 x x x 7 x 7 a dir. Denklemde x 7 a yazalım. 7 a a 7 a a 1 0 49 14a a : Çözüm 2 2 2 2 7a a a 1 0 2a 20a 48 0 a 10a 24 0 a 4 a 6 0 a 4 ve a 6 dır. Cevap: B 126
2 1 2 1 2 x 4x c 0 denkleminin kökleri x ve x dir. x 2x 7 olduğuna göre, c kaçtır? A) 5 B) 3 C) 1 D) 3 E) 5 www.matematikkolay.net 1 2 1 2 1 2 4 Kökler toplamı x x 4 tür. 1 x x 4 -/ x 2x 7 taraf tara : fa çıkaralım Çözüm 2 2 2 2 2 3x 4 7 3x 3 x 1 dir. 1 denklemi sağlayan bir kök olduğuna göre denklemde yerine yazalım. x 4x c 0 ( 1) 4( 1) c 0 1 4 c 0 c 5 buluruz. 14
2 1 2 1 2 x 3x 2m 0 denkleminin kökleri x ve x dir. 2 Bu kökler arasında x 1 bağıntısı var sa, m n x in alabileceği değerleri toplamı kaçtır? A) 1 B) 3 C) 6 D) 3 E) 4 www.matematikkolay.net 2 1 2 2m 1 2 1 2 2 2 2 x 3x 2m 0 c Kökler çarpımı x x 2m dir. a 2 x x 2 2m 2 x 1 ise 1 1 x x x 2 So : x 2m Çözüm 2 2 2 ruda verilen denklemde x, yerine 2m 2 yazarsak denklem sağlanır. (2m 2) 3(2m 2) 2m 0 4m 8m 4 6m 6 2m 0 4m 4m 2 0 b 4 Kökler toplamı 1 buluruz. a 4 16
www.matematikkolay.net 2 1 2 1 2 x 2 m x m 1 0 denkleminin x ve x kökleri arasında 1 1 1 bağıntısı var sa m kaçtır? x x 2 A) 2 B) 1 C) 1 D) 2 E) 3 2 1 2 1 2 x x ax bx c 0 denkleminde b c kökler toplamı kökler çarpımı dır. a a 1 1 1 2 : x x Çözüm 2 1 1 2 x x 1 ise x x 2 Kökler toplamı 1 Kökler çarpımı 2 2 m 1 1 2 m 1 4 2m m 1 m 1 2 m 1 2 1 4 1 m 2m 3 3m m 1 buluruz. 110

