Soru Sor sayfası kullanılarak 2.Dereceden Denklemler konusu altında Değişken değiştirme (2.dereceden denklem) ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

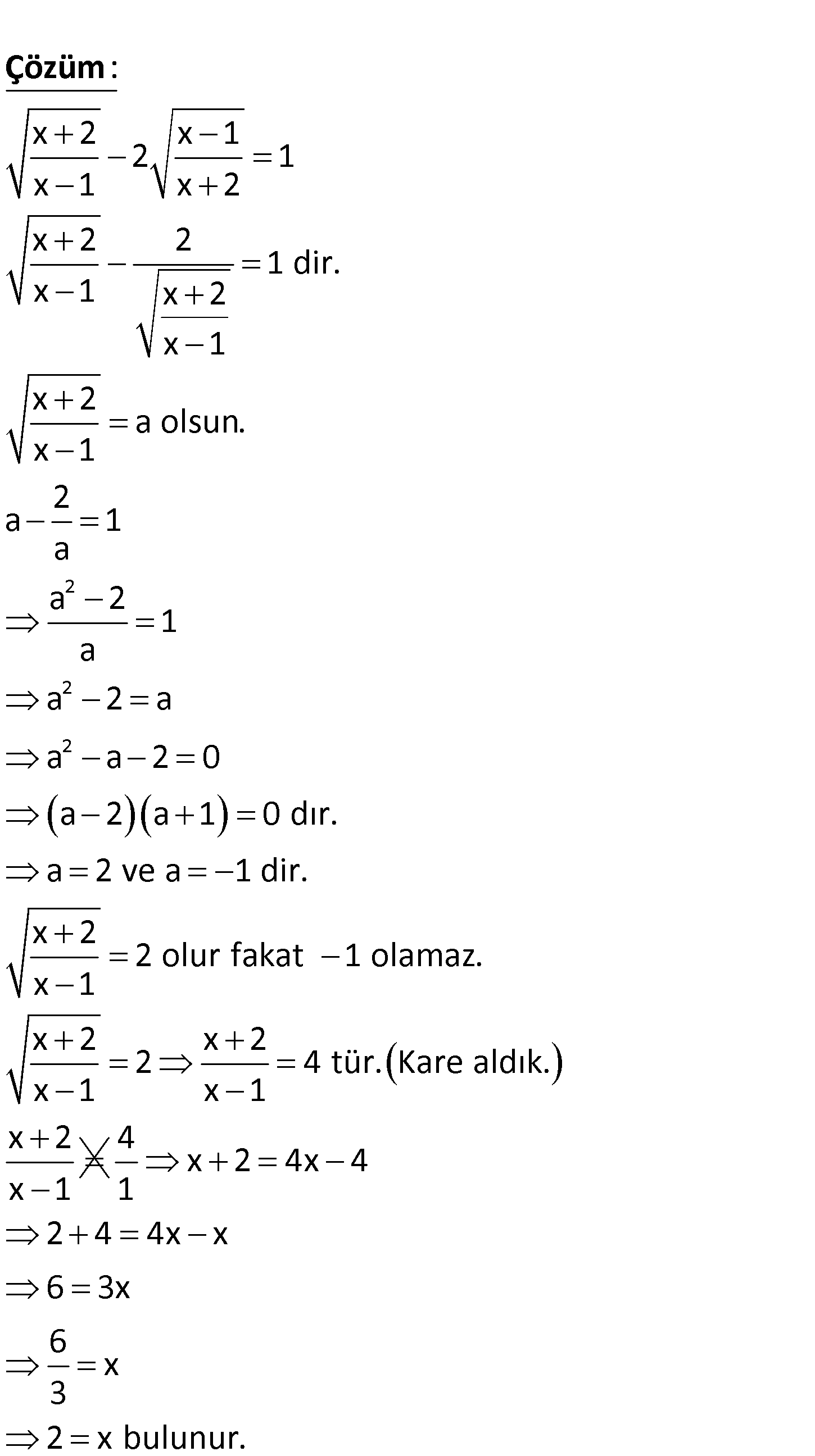
2.SORU


3.SORU

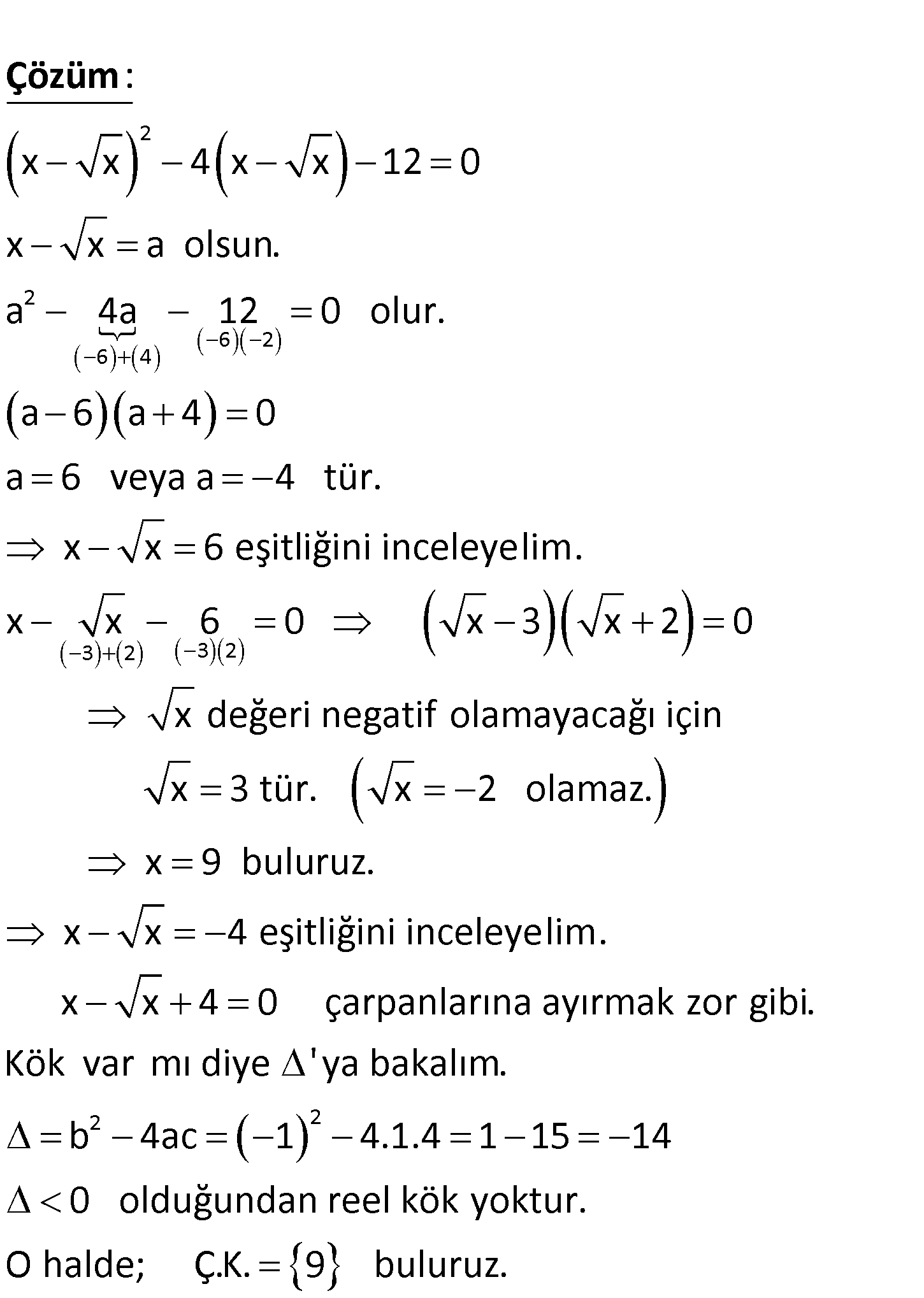
4.SORU

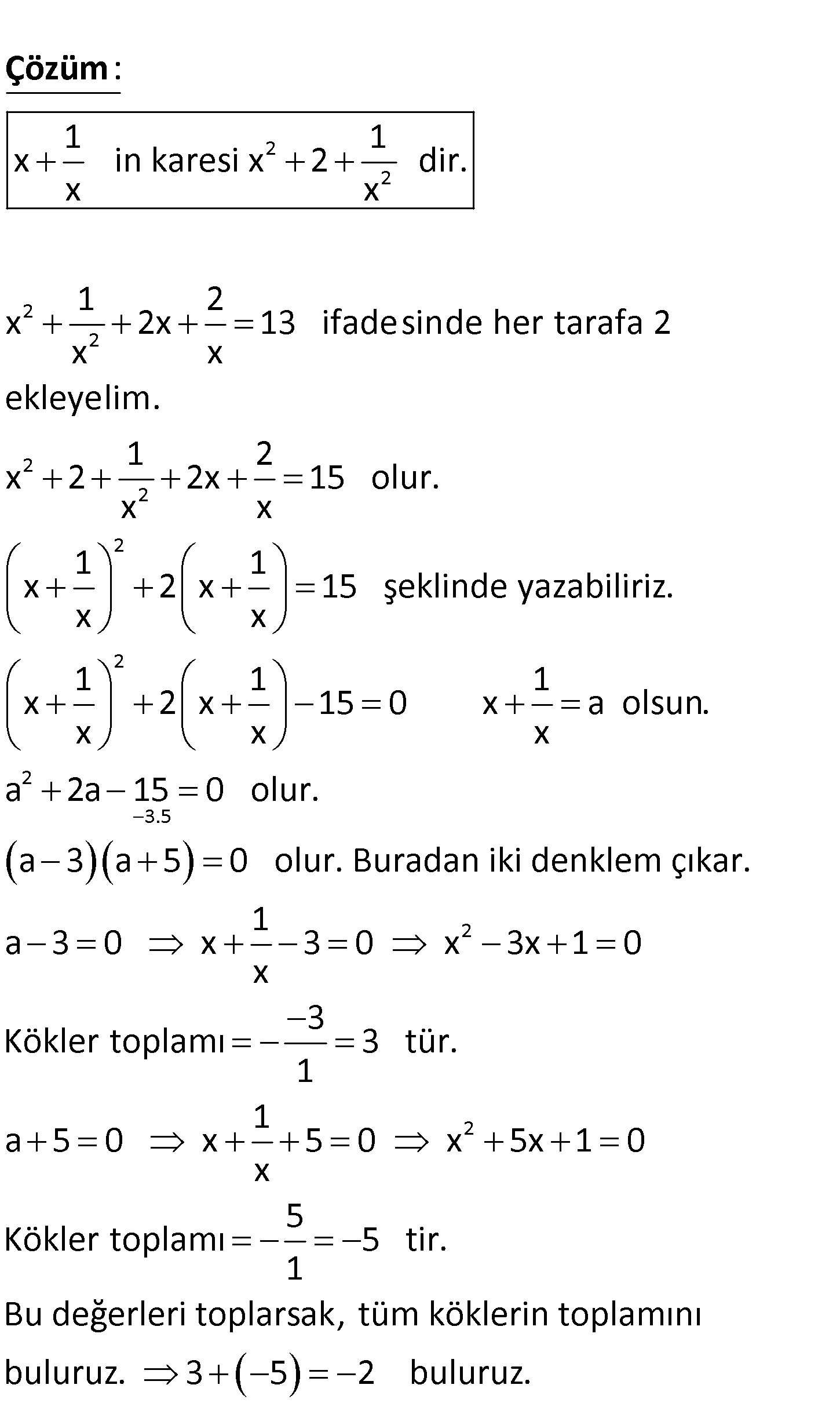
5.SORU
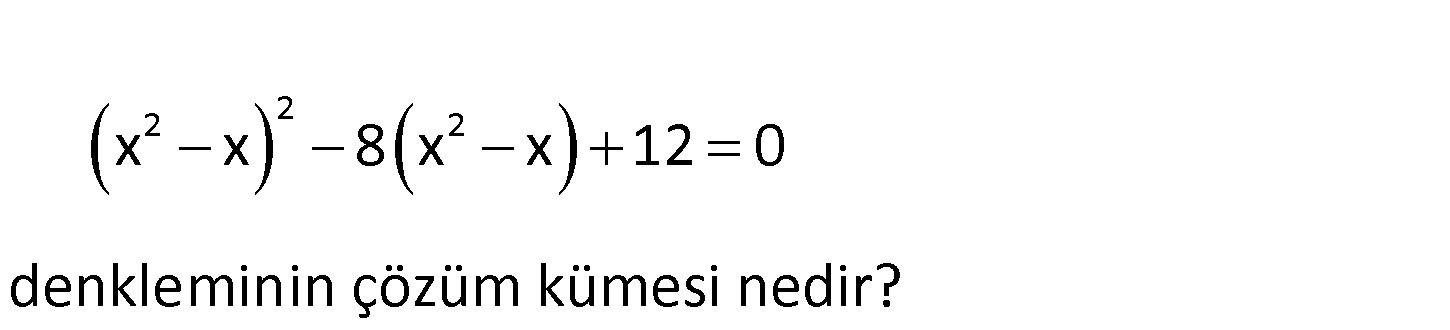
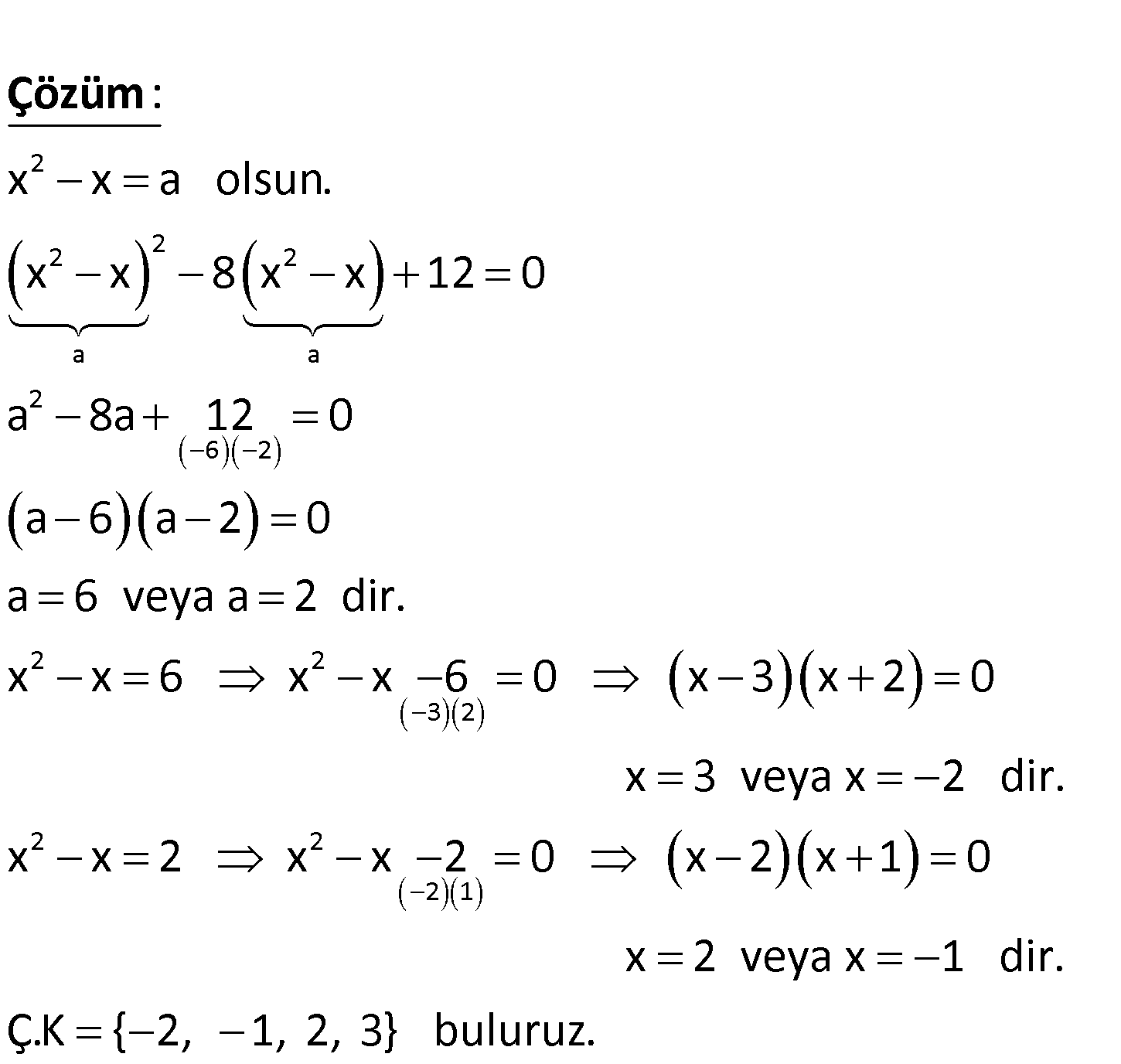
6.SORU

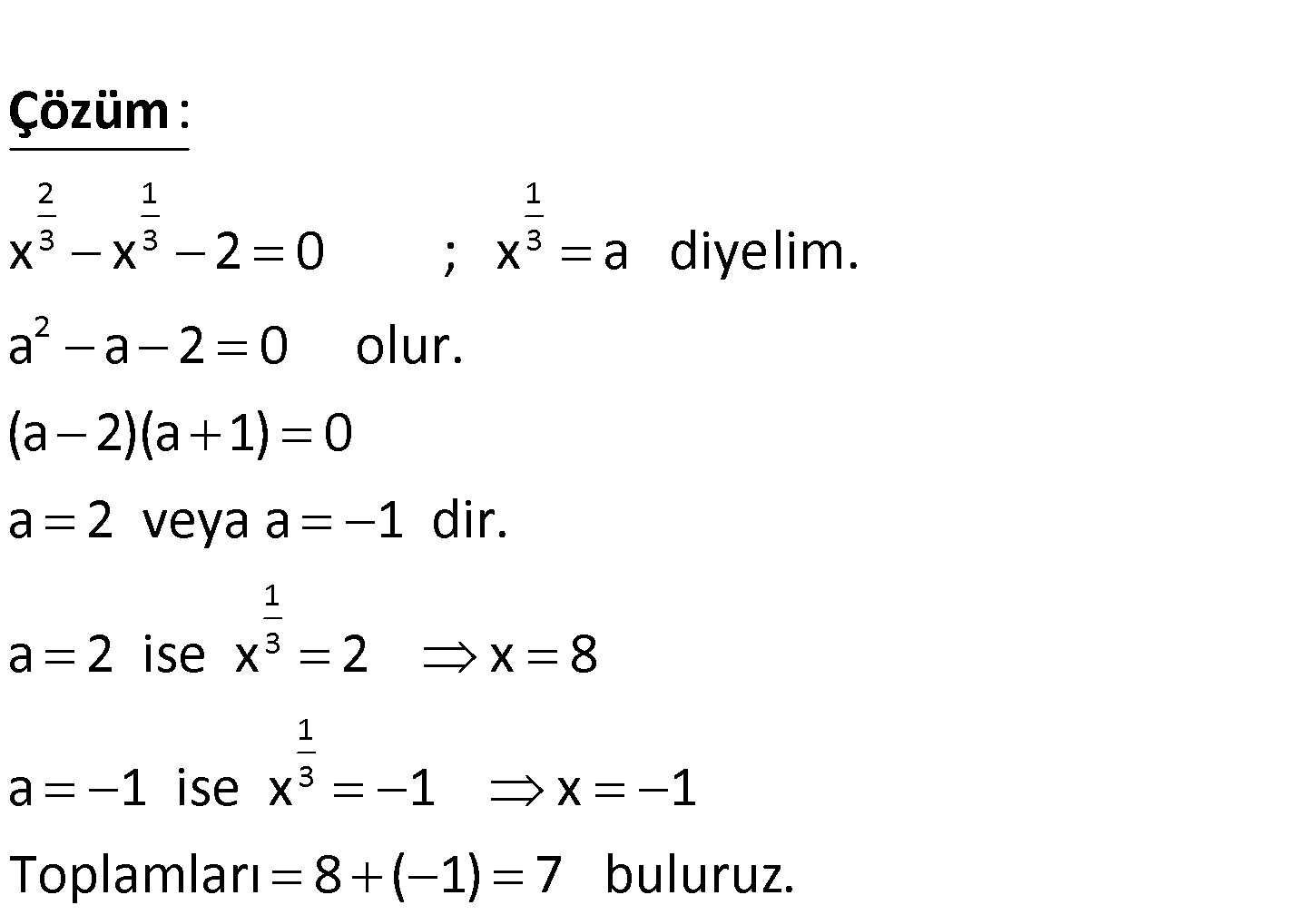
7.SORU
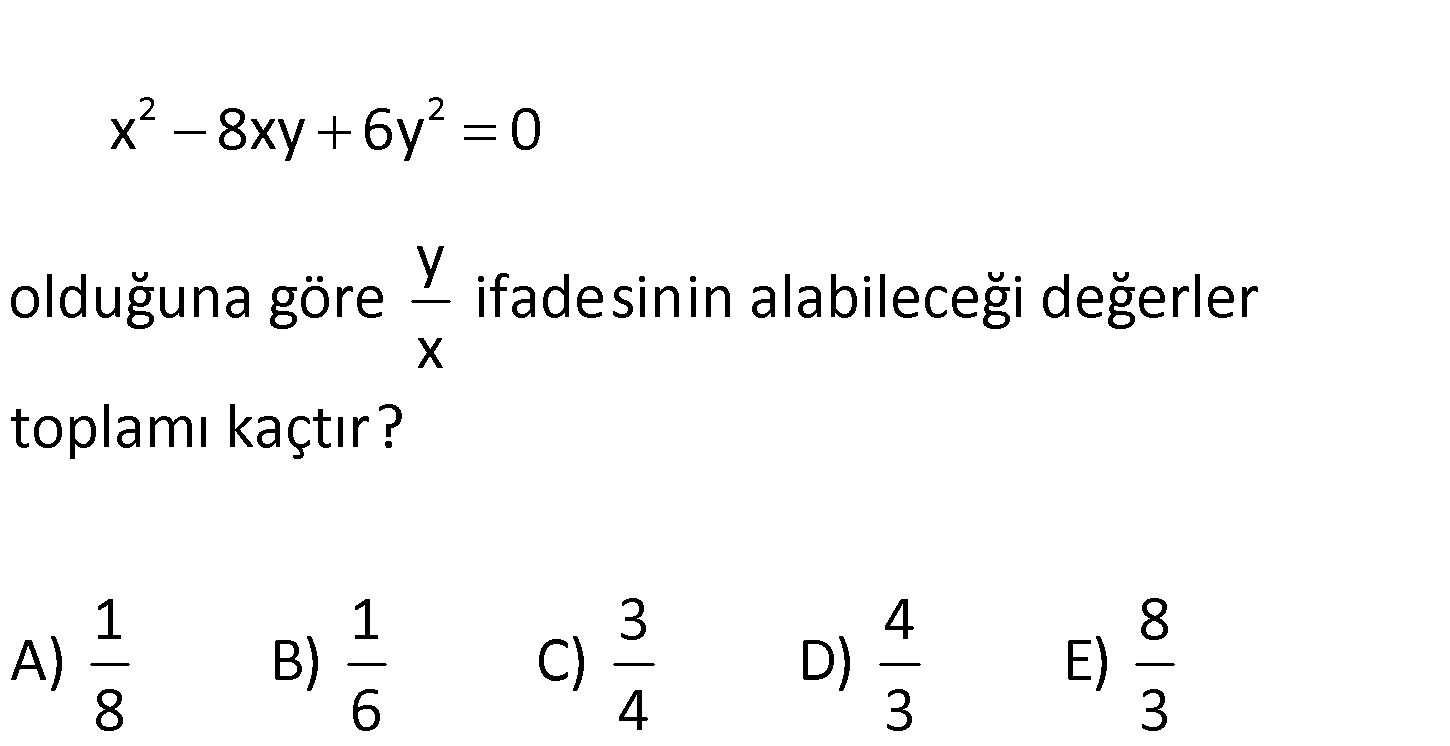

8.SORU
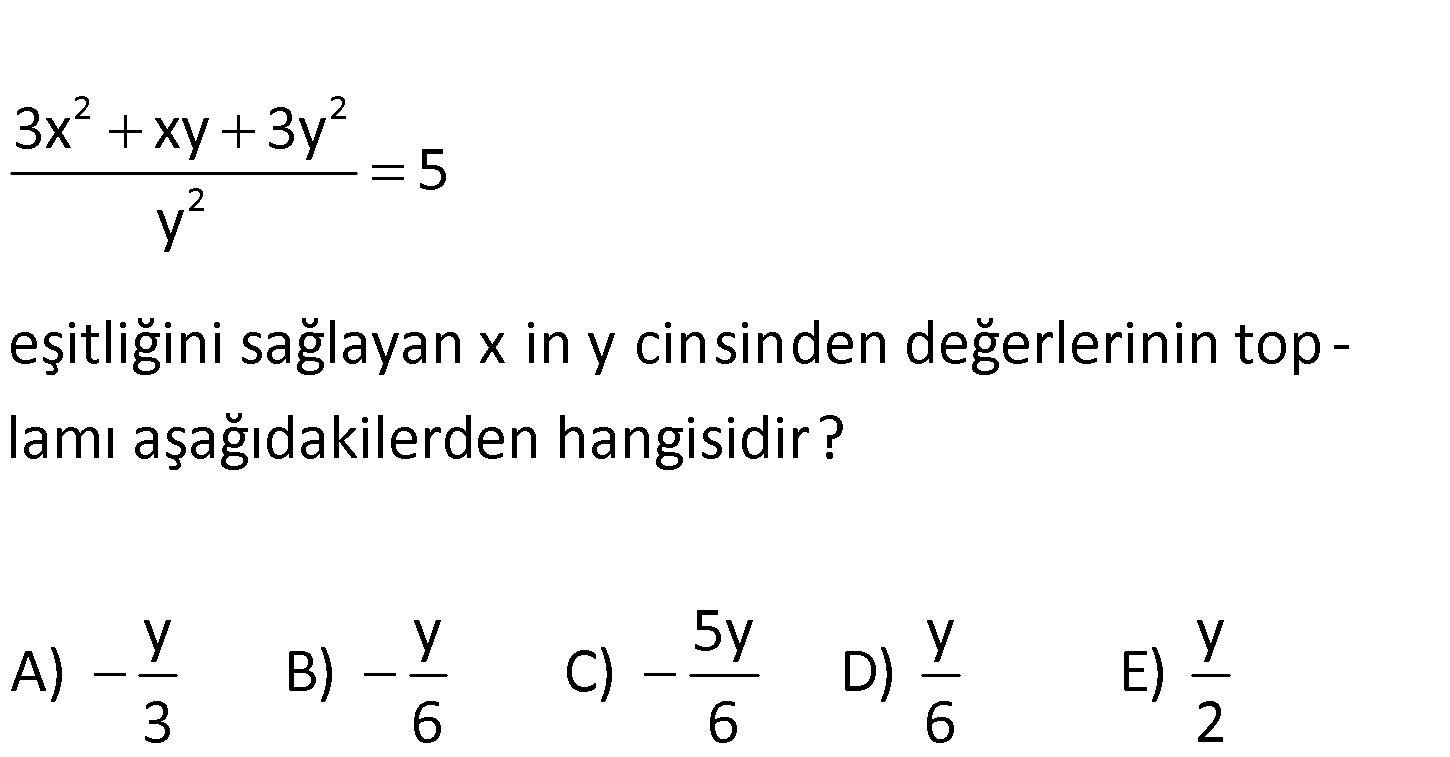
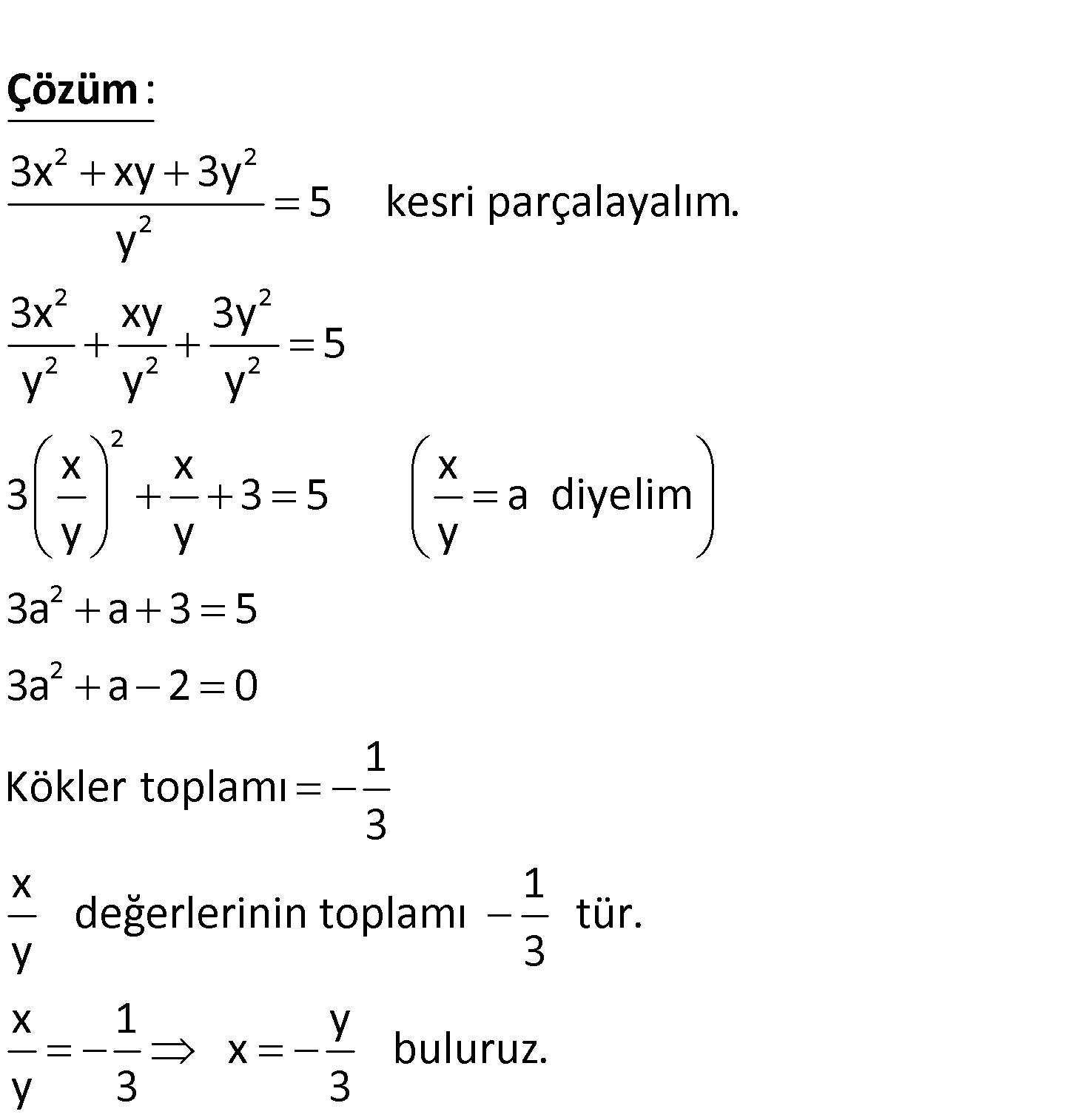
9.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
x 2 x 1 2 1 x 1 x 2 denkleminin çözüm kümesi aşağıdakilerden hangi – dir? A) B) R C) 1 D) 1 E) 1,2 www.matematikkolay.net 2 2 2 x 2 x 1 2 1 x 1 x 2 x 2 2 1 dir. x 1 x 2 x 1 x 2 a olsun. x 1 2 a 1 a a 2 1 a a 2 a a a 2 0 a 2 a : 1 0 Çözüm dır. a 2 ve a 1 dir. x 2 2 olur fakat 1 olamaz. x 1 x 2 x 2 2 4 tür. Kare aldık. x 1 x 1 x 2 x 1 4 x 2 4x 4 1 2 4 4x x 6 3x 6 x 3 2 x bulunur. www.matematikkolay.net 82
x x 2 x x 3 2 24 3 2 95 0 denkleminin çözüm kümesi aşağıdakilerden hangi – dir? A) 2 B) 2, 3 C) 1, 2 D) 3, 4 E) 2, 4 x x 2 x x x x 2 19 5 19 5 3 2 25 3 2 95 0 3 2 a olsun. a 24a 95 0 olur. a 19 a 5 0 a 19 veya a 5 t : Çözüm x x 2 2 x x ir. 3 2 5 eşitliği x 2 olduğunda sağlanır. 3 2 9 5 4 tür. 3 2 19 eşitliği x 3 olduğunda sağlanır. 3 3 3 2 27 8 19 dur. Ç.K. 2,3 buluruz. 83
www.matematikkolay.net x x 2 x x 3 2 24 3 2 95 0 denkleminin çözüm kümesi aşağıdakilerden hangi – dir? A) 2 B) 2, 3 C) 1, 2 D) 3, 4 E) 2, 4 2 2 6 2 6 4 x x 4 x x 12 0 x x a olsun. a 4a 12 0 olur. a 6 a 4 0 a 6 veya a 4 tür. x x 6 e : Çözüm 3 2 3 2 şitliğini inceleyelim. x x 6 0 x 3 x 2 0 x değeri negatif olamayacağı için x 3 tür. x 2 olamaz. x 9 buluruz. x x 4 eşitliğini inceleyelim. x x 2 2 4 0 çarpanlarına ayırmak zor gibi. Kök var mı diye ‘ ya bakalım. b 4ac 1 4.1.4 1 15 14 0 olduğundan reel kök yoktur. O halde; Ç.K. 9 buluruz. 84
2 2 1 2 x 2x 13 x x denkleminin gerçek köklerinin toplamı kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 www.matematikkolay.net 2 2 2 2 2 2 1 1 x in karesi x 2 dir. x x 1 2 x 2x 13 ifadesinde her tarafa 2 x x ekleyelim : . 1 x 2 x Çözüm 2 2 2 03.May 2 2x 15 olur. x 1 1 x 2 x 15 şeklinde yazabiliriz. x x 1 1 1 x 2 x 15 0 x a olsun. x x x a 2a 15 0 olur. a 3 a 5 0 olur. Buradan iki denklem çıkar. 1 a 3 0 x 3 0 x 2 2 x 3x 1 0 3 Kökler toplamı 3 tür. 1 1 a 5 0 x 5 0 x 5x 1 0 x 5 Kökler toplamı 5 tir. 1 Bu değerleri toplarsak, tüm köklerin toplamını buluruz. 3 5 2 buluruz. 90
2 2 2 x x 8 x x 12 0 denkleminin çözüm kümesi nedir? 2 2 2 2 a a 2 6 2 2 2 x x a olsun. x x 8 x x 12 0 a 8a 12 0 a 6 a 2 0 a 6 veya a 2 dir. x x 6 x : Çözüm 3 2 2 2 2 1 x 6 0 x 3 x 2 0 x 3 veya x 2 dir. x x 2 x x 2 0 x 2 x 1 0 x 2 veya x 1 dir. Ç.K { 2, 1, 2, 3} buluruz. 122
2 1 3 3 x x 2 0 denklemini sağlayan x gerçek sayılarının toplamı kaçtır? A) 8 B) 7 C) 5 D) 4 E) 3 www.matematikkolay.net 2 1 1 3 3 3 2 x x 2 0 ; x a diyelim. a a 2 0 olur. (a 2)(a 1) 0 a 2 veya a 1 : dir. a Çözüm 1 3 1 3 2 ise x 2 x 8 a 1 ise x 1 x 1 Toplamları 8 ( 1) 7 buluruz. 8
2 2 x 8xy 6y 0 y olduğuna göre ifadesinin alabileceği değerler x toplamı kaçtır? 1 1 3 A) B) C) D 8 6 4 4 8 ) E) 3 3 2 2 2 2 2 2 2 2 x 8xy 6y 0 her tarafı x ye bölelim. x 8xy 6y 0 x x x y 1 8 6 0 y x y 6 x : Çözüm 2 2 x y 8 1 0 t dersek; y x 6t 8t 1 0 8 4 Kökler toplamı; buluruz. 6 3 62
2 2 2 3x xy 3y 5 y eşitliğini sağlayan x in y cinsinden değerlerinin top – lamı aşağıdakilerden hangisidi r? y y 5y y y A) B) C) D) E) 3 6 6 6 2 www.matematikkolay.net 2 2 2 2 2 2 2 2 2 3x xy 3y 5 kesri parçalayalım. y 3x xy 3y 5 y y y x x x 3 3 5 a diyeli y y : y Çözüm 2 2 m 3a a 3 5 3a a 2 0 1 Kökler toplamı 3 x 1 değerlerinin toplamı tür. y 3 x 1 y x buluruz. y 3 3 15
2 1 2 3 3 1 2 x 18x 1 0 denkleminin kökleri x ve x dir. Buna göre, x x toplamı kaçtır? A) 2 B) 1 C) 1 D) 2 E) 3 www.matematikkolay.net 3 3 3 3 3 3 3 3 3 3 1 2 1 2 1 2 1 2 Not : a b (a b) 3ab(a b) dir. Buna göre; x x x x 3 x . x x x şeklinde bir : denkl Çözüm 3 3 1 2 3 3 1 2 1 2 Kökler toplamı Kökler çarpımı 3 3 3 2 3 9 em oluşturabiliriz. x x k olsun. x x k 3 x .x .k 18 k 3 1.k 18 k 3k 18 k(k 3) k 3 buluruz. 66

