Soru Sor sayfası kullanılarak 2.Dereceden Denklemler konusu altında 2.dereceden denklem sistemi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
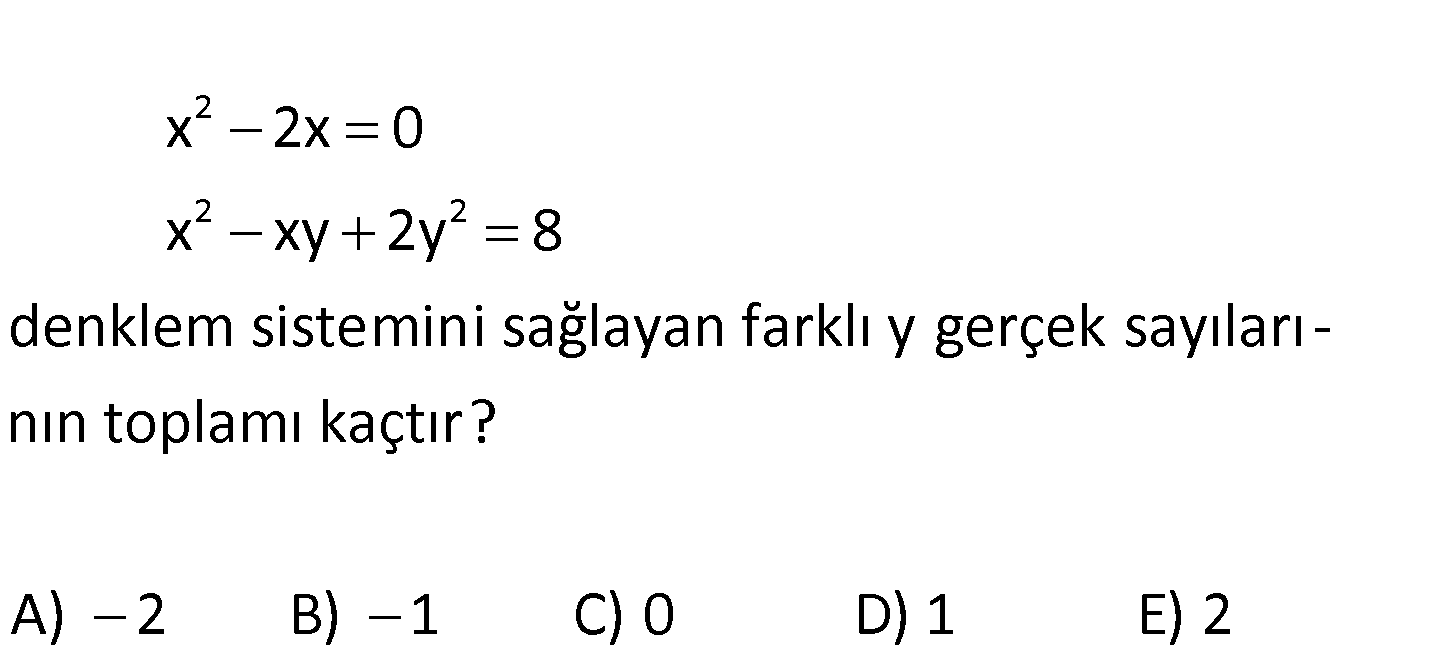

2.SORU

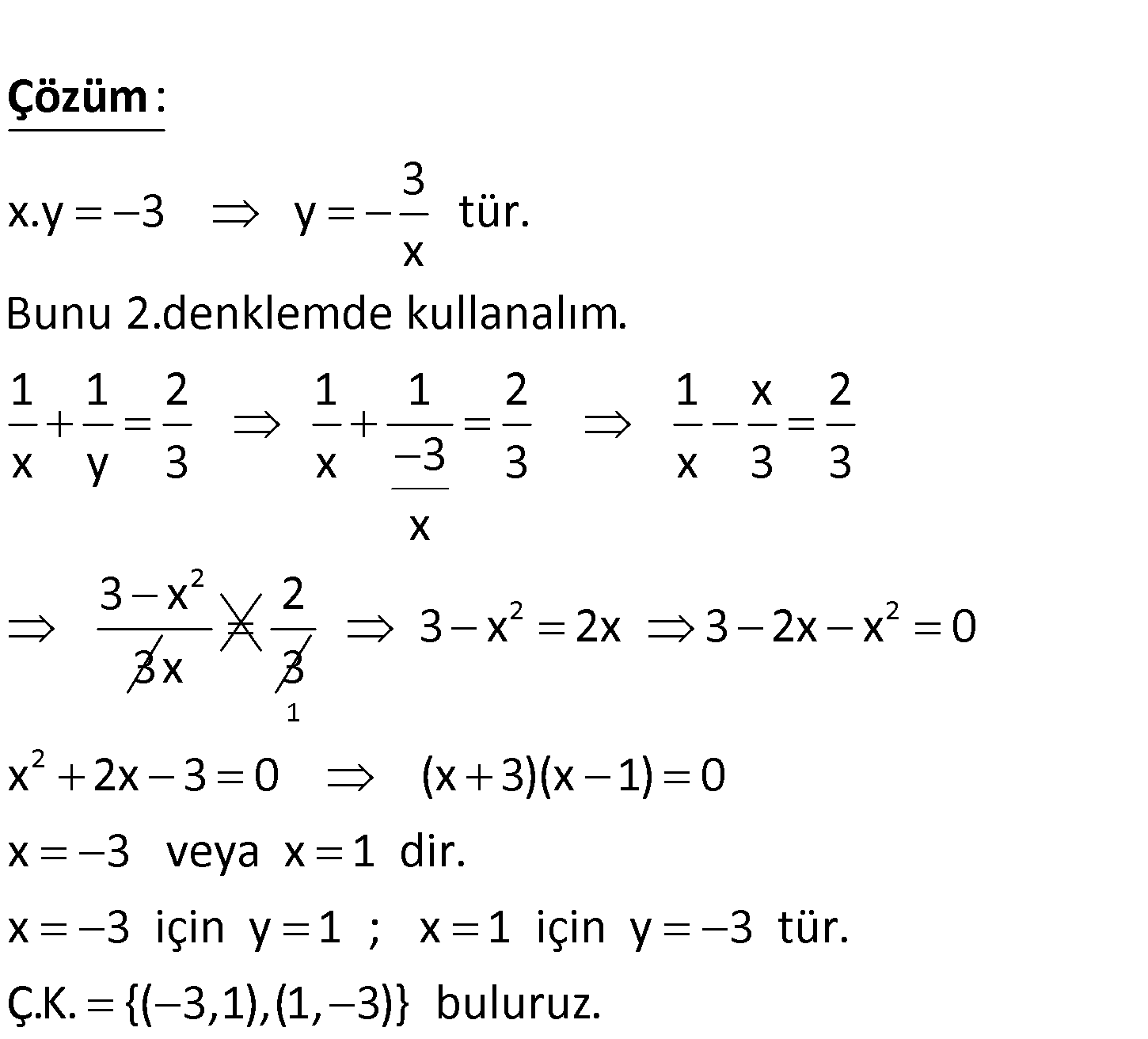
3.SORU


4.SORU
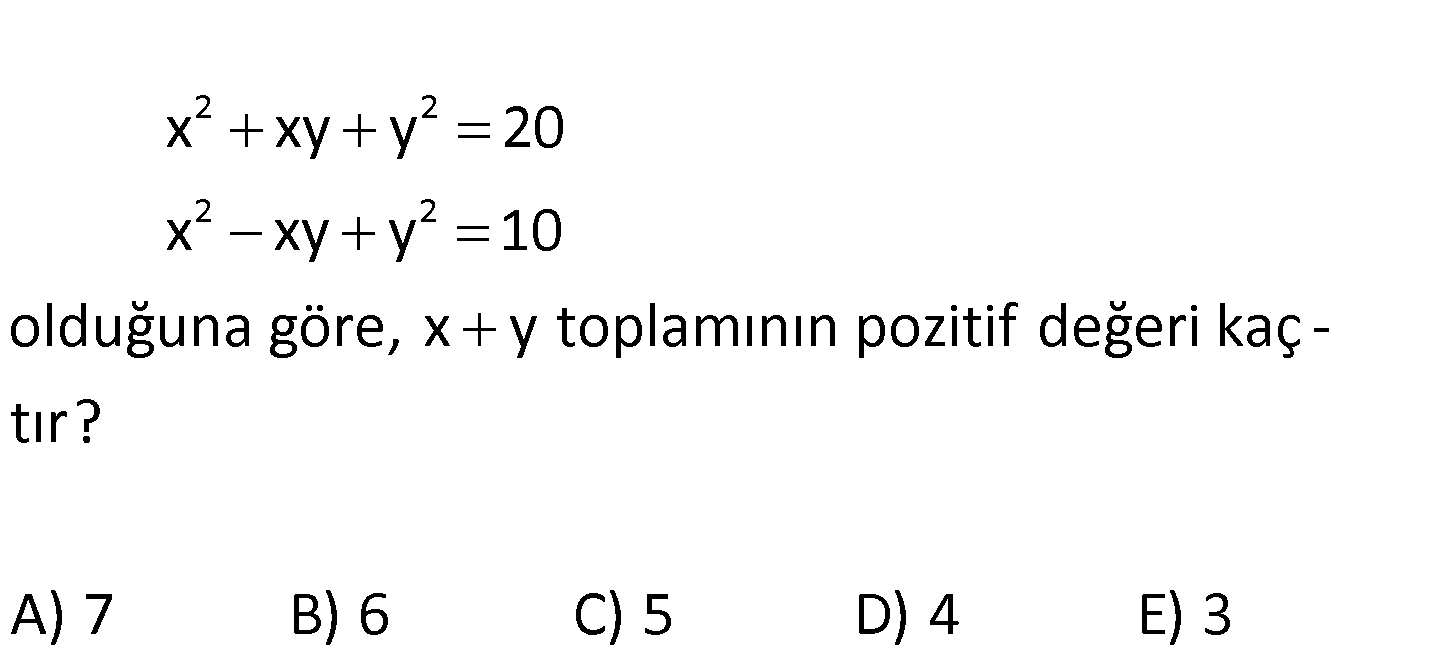
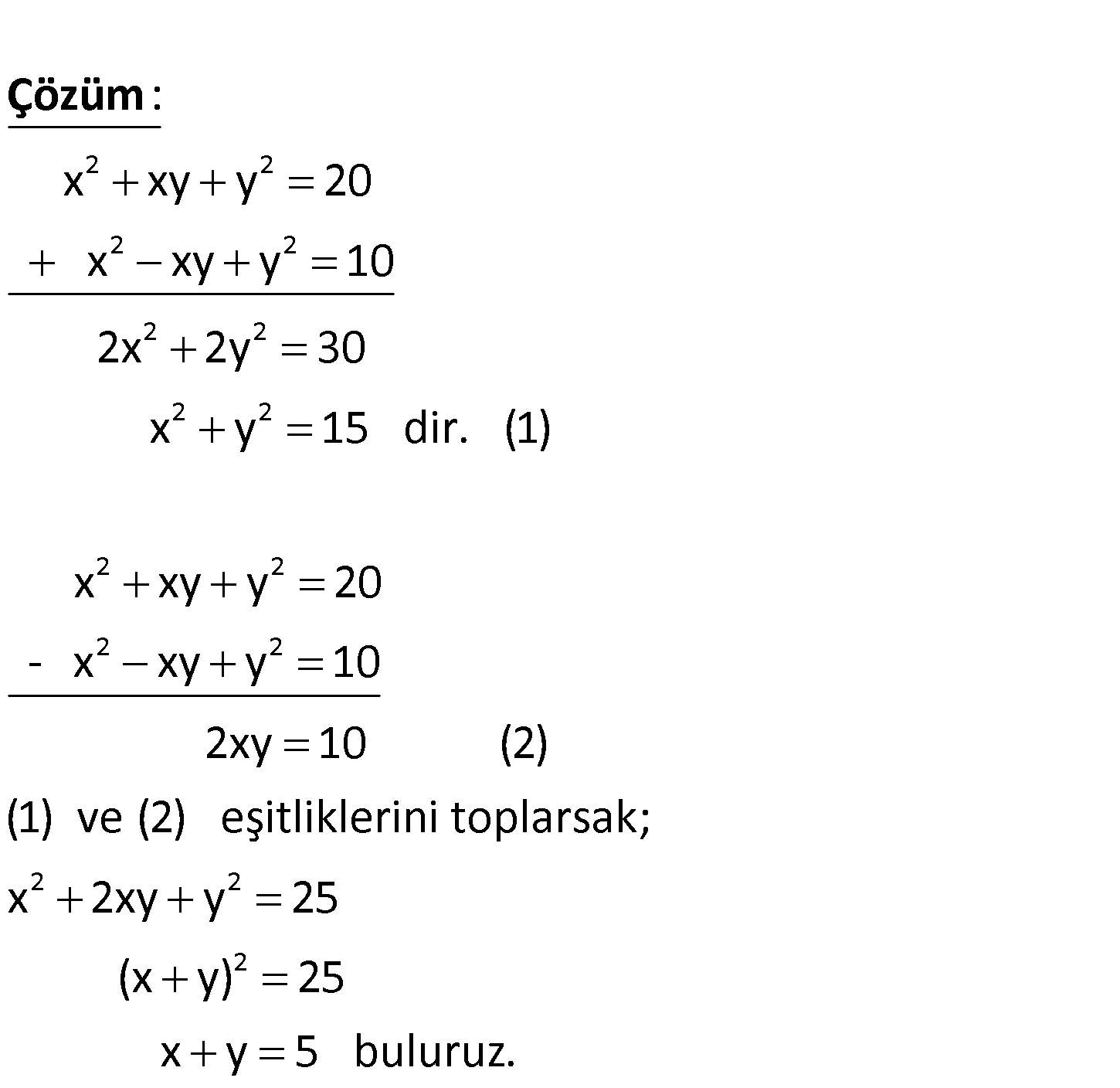
5.SORU


6.SORU


7.SORU
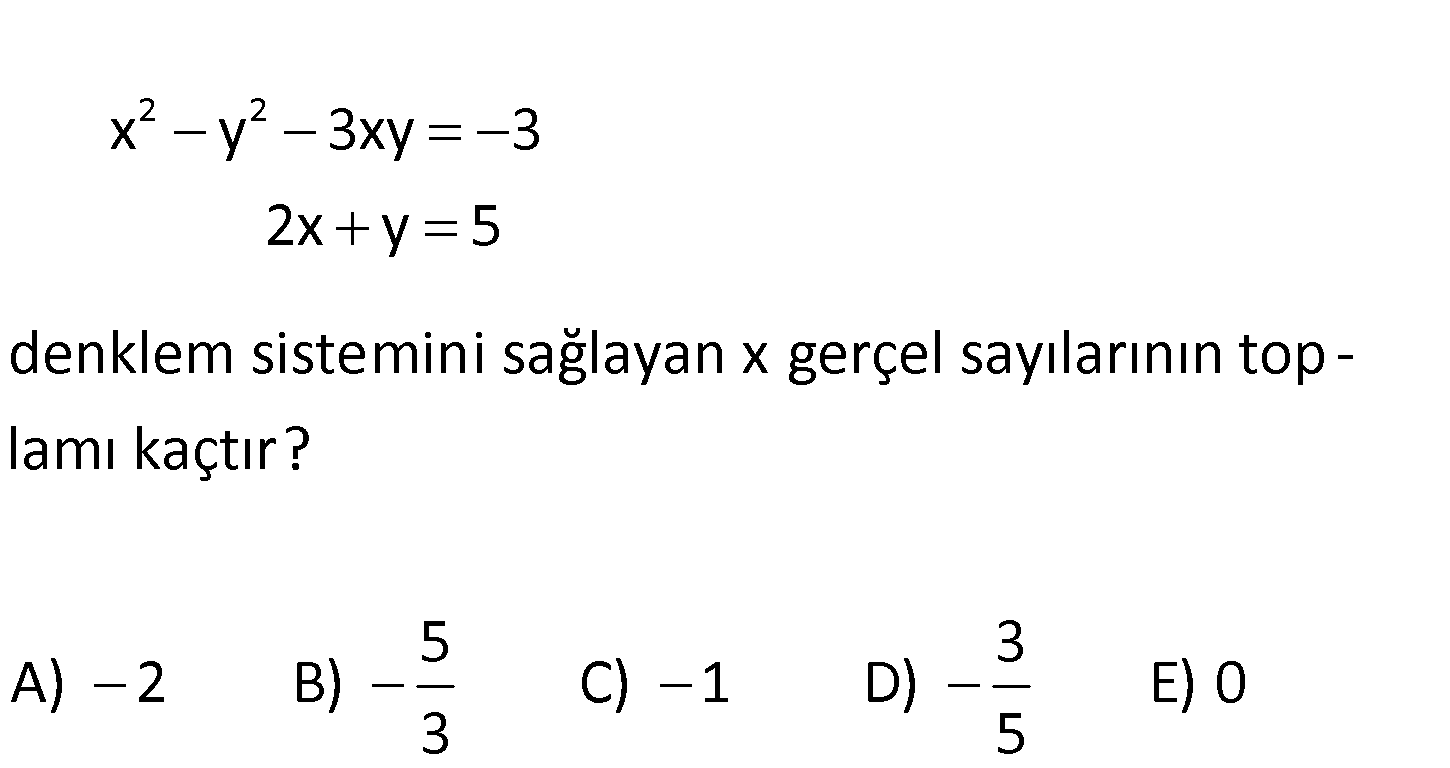

8.SORU


9.SORU


Konu Anlatımı veya Daha Fazla Soru için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net 2 2 2 x 2x 0 x xy 2y 8 denklem sistemini sağlayan farklı y gerçek sayıları – nın to plamı kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 2 x 2x 0 x(x 2) 0 x 0 veya x 2 dir. Bu değerleri 2.denklemde kullanalım. x 0 içi : n x Çözüm 2 2 2 2 2 2 2 2 2 2 2 2 xy 2y 8 0 0.y 2y 8 y 4 y 2 veya y 2 dir. x 2 için x xy 2y 8 2 2.y 2y 8 4 2.y 2y 8 2y 2y 4 0 y y 2 0 (y 2)(y 1) 0 y 2 veya y 1 dir. y’nin alabileceği fark lı değerler : 2, 1 ve 2 Toplamı 2 ( 1) 2 1 buluruz. 3
www.matematikkolay.net x.y 3 1 1 2 x y 3 denklem sistemininin çözüm kümesi aşağıdakiler – den hangisidir? A) 3, 1 , 1, 2 B) 3, 1 , 1, 3 C) 3, 1 D) 1, 3 E) 1, 1 3 x.y 3 y tür. x Bunu 2.denklemde kullanalım. 1 1 2 1 1 2 1 x 2 x y 3 x 3 3 x 3 : 3 x Çözüm 2 3 x 3 x 2 3 2 2 1 2 3 x 2x 3 2x x 0 x 2x 3 0 (x 3)(x 1) 0 x 3 veya x 1 dir. x 3 için y 1 ; x 1 için y 3 tür. Ç.K. {( 3,1),(1, 3)} buluruz. 4
www.matematikkolay.net 2 y 8x 2x y 6 denklem sisteminini sağlayan x gerçek sayılarının toplamı kaçtır? A ) 5 B) 6 C) 7 D) 8 E) 9 2 2 2 2x y 6 ise 2x 6 y dir. 1.denklemde y’nin yerine bunu yazalım. y 8x (2x 6) 8x 4x : Çözüm 2 2 2 24x 36 8x 4x 32x 36 0 (Her tarafı 4’e bölelim) x 8x 9 0 b Not : ax bx c Kökler toplamı= dır. a b 8 Kökler toplamı 8 buluruz. a 1 5
2 2 2 2 x xy y 20 x xy y 10 olduğuna göre, x y toplamının pozitif değeri kaç – tır? A ) 7 B) 6 C) 5 D) 4 E) 3 www.matematikkolay.net 2 2 2 2 2 2 2 2 2 x xy y 20 x xy y 10 2x 2y 30 x y 15 dir. (1) : x Çözüm 2 2 2 2 2 2 xy y 20 – x xy y 10 2xy 10 (2) (1) ve (2) eşitliklerini toplarsak; x 2xy y 25 (x y) 25 x y 5 buluruz. 6
www.matematikkolay.net 2 2 x y 6 x y 20 sisteminin çözüm kümesi aşağdakilerden hangisi – dir? A) 4, 2 B) 4, 2 , 2,4 C ) 2, 4 D) 0, 6 E) 4, 2 2 2 20 2 2 2 20 16 2 x y 6 kare alalım. x y 2xy 36 olur. 2xy 16 dır. x y x y 2xy x : y 4 Çözüm x y 2 veya 2 dir. x y 2 olduğunda; x y 6 2x 8 x 4 ve y 2 dir. x y 2 olduğunda; x y 6 2x 4 x 2 ve y 4 tür. Ç.K {(4,2),(2,4)} buluruz. 80
www.matematikkolay.net 2 2 x 2xy y y 2x 1 sisteminde x in alacağı değerlerin çarpımı kaçtır? dir? 6 63 3 A) B) C) 7 4 2 1 D) E) 7 7 7 2 2 2 2 2 2 2 2 2 : x 2xy y denkleminde y yerine y 2x 1 yazalım x 2x 2x 1 2x 1 x 4x 2x 4x 4x 1 3x 2x 4x 4 Çözüm 2 2 x 1 7x 6x 1 0 olur. c Not : ax bx c denkleminde kökler çarpımı a 1 1 Kökler çarpımı buluruz. 7 7 www.matematikkolay.net 81
2 2 x y 3xy 3 2x y 5 denklem sistemini sağlayan x gerçel sayılarının top – lam ı kaçtır? 5 3 A) 2 B) C) 1 D) E) 0 3 5 www.matematikkolay.net 2 2 2 2 2x y 5 ise y 5 2x tir. x y 3xy 3 denkleminde y 5 2x yazalım. x 5 2x 3x. 5 2 : Çözüm 2 2 2 2 2 2 2 x 3 x 25 20x 4x 15x 6x 3 x 25 20x 4x 15x 6x 3 3x 5x 22 0 5 Kökler toplamı buluruz. 3 108
2 ax bx 2 0 denkleminde 2a b 1 bağıntısı var sa, aşağıdaki – lerden hangisi bu denklemin bir kö küdür? A) 3 B) 2 C) 1 D) 1 E) 2 2 2 2a b 1 2a 1 b dir. Denklemde b’nin a cinsinden değerini yazalım. ax bx 2 0 a ( : x Çözüm 2 0 2a 1)x 2 0 ax 2ax x 2 ax(x 2) (x 2) 0 (x 2)(ax 1) 0 x 2 denklemin bir köküdür. www.matematikkolay.net 17
2 2 2 x 2y 3x 3 denklem sisteminin kaç farklı 2y 4x 4 0 kökü vardır? A) 5 B) 4 C) 3 D) 2 E) 1 2 2 2 2 x 2y 3x 3 0 2y 4x 4 0 taraf tarafa toplayalım. x x 1 0 buradan 2 f l : ark ı x Çözüm değeri çıkar. 2 farklı x değerini sırasıyla denklemlerden birine yerleştirirsek; 2’şer tane y değeri buluruz. Böylece 4 farklı x, y ikilisi oluşur. Cevap: 4 www.matematikkolay.net 88

