Soru Sor sayfası kullanılarak 1.Dereceden Denklemler konusu altında Üç Bilinmeyenli Denklem ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
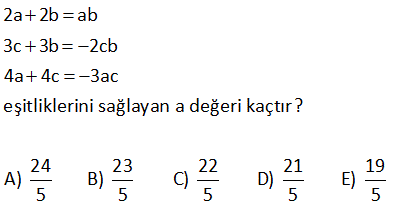

2.SORU
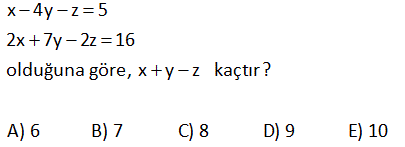

3.SORU
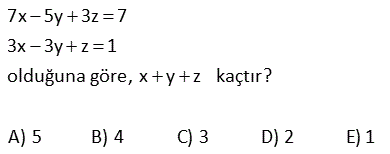

4.SORU


5.SORU
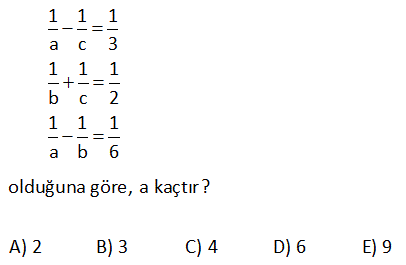

6.SORU
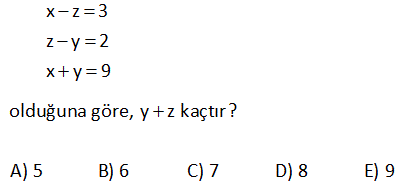

7.SORU
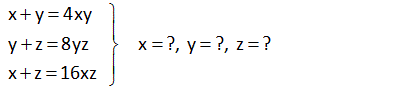
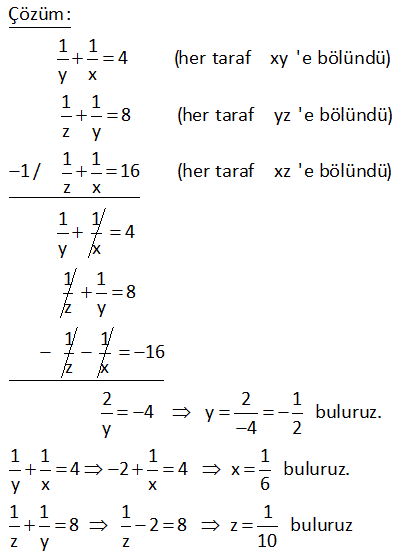
8.SORU
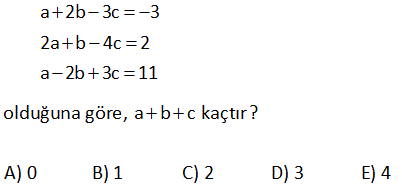

9.SORU
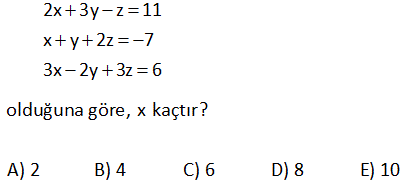

10.SORU
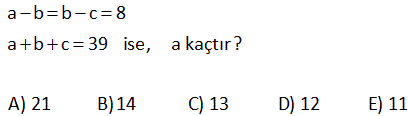

11.SORU
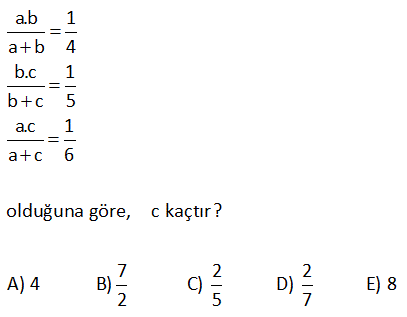
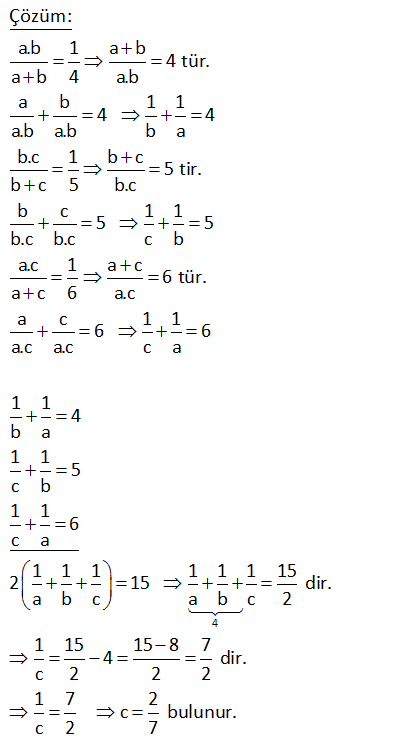
12.SORU

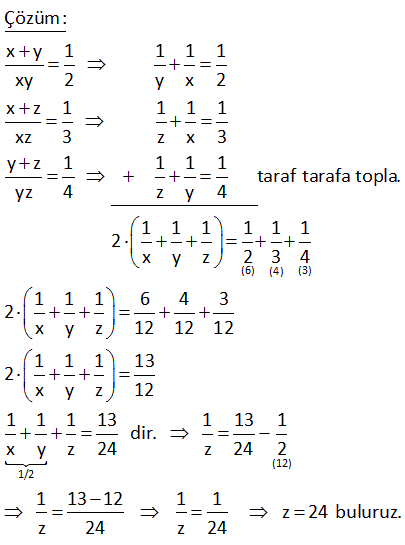
13.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
2a 2b ab 3c 3b 2cb 4a 4c 3ac eşitliklerini sağlayan a değeri kaçtır? 24 23 22 21 19 A) B) C) D) E) 5 5 5 5 5 www.matematikkolay.net Çözüm: 2a 2b ab (Her tarafı ab’ye bölelim) 3c 3b 2cb (Her tarafı cb’ye bölelim) 4a 4c 3ac (Her tarafı ac’ye bölelim) 2 2 06.Oca b a 3 3 sadec 04.Şub b c 4 4 03.Mar c a e a’lı terim kalacak şekilde genişletelim. 12 b 12 6 a 12 b 12 c 8 12 c 12 9 a 24 5 a 24 a buluruz. 5 5 x 4y z 5 2x 7y 2z 16 olduğuna göre, x y z kaçtır? A) 6 B) 7 C) 8 D) 9 E) 10 Çözüm: x 4y z 5 2x 7y 2z 16 taraf tarafa toplayalım. 3x 3y 3z 21 3(x y z) 21 x y z 7 buluruz. 10 7x 5y 3z 7 3x 3y z 1 olduğuna göre, x y z kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 www.matematikkolay.net Çözüm: 7x 5y 3z 7 -2 / 3x 3y z 1 2 ile genişletelim. 7x 5y 3z 7 6x 6y 2z 2 taraf tarafa toplayalım. x y z 5 buluruz. 11 A B 72 A C 48 B C 64 A B C ? Çözüm: A B 72 A C 48 B C 64 taraf tarafa toplayalım. 2A 2B 2C 72 48 64 2(A B C) 184 A B C 92 buluruz. 22 www.matematikkolay.net 1 1 1 a c 3 1 1 1 b c 2 1 1 1 a b 6 olduğuna göre, a kaçtır? A) 2 B) 3 C) 4 D) 6 E) 9 Çözüm: 1 1 a c 1 3 1 b 1 c 1 2 1 1 a b (2) (3) 1 taraf tarafa toplayalım. 6 2 1 1 1 a 3 2 6 2 2 3 1 2 1 a 2 buluruz. a 6 a 26 x z 3 z y 2 x y 9 olduğuna göre, y z kaçtır? A) 5 B) 6 C) 7 D) 8 E) 9 www.matematikkolay.net Çözüm: x z 3 z y 2 x y 9 taraf tarafa toplayalım. 2x 3 2 9 2x 14 x 7 dir. x y 9 idi y 2 dir. z y 2 idi z 4 tür. Buna göre; y z 2 4 6 buluruz. 27 www.matematikkolay.net x y 4xy y z 8yz x ?, y ?, z ? x z 16xz Çözüm: 1 1 4 (her taraf xy ‘e bölündü) y x 1 1 8 (her taraf yz ‘e bölündü) z y 1 1 1 / 16 (her taraf xz ‘e bölündü) z x 1 1 y x 4 1 z 1 8 y 1 z 1 x 16 2 2 1 4 y buluruz. y 4 2 1 1 1 1 4 2 4 x buluruz. y x x 6 1 1 1 1 8 2 8 z buluruz z y z 10 www.matematikkolay.net 28 a 2b 3c 3 2a b 4c 2 a 2b 3c 11 olduğuna göre, a b c kaçtır? A) 0 B) 1 C) 2 D) 3 E) 4 Çözüm: a 2b 3c 3 (I) 2a b 4c 2 (II) a 2b 3c 11 (III) I. ve III. denklemleri alt alta toplarsak; a 2b 3c 3 a 2b 3c 4 4 11 2a 8 a 4 tür. II. ve III. denklemlerde a yı yerine yazalım; 2a b 4c 2 b 4c 6 dır. a 2b 3c 11 2b 3c 7 dir. b 4c 6 2b 3c 7 b c 1 b c 1 dir. a b c 4 ( 1) 3 buluruz. www.matematikkolay.net 29 2x 3y z 11 x y 2z 7 3x 2y 3z 6 olduğuna göre, x kaçtır? A) 2 B) 4 C) 6 D) 8 E) 10 Çözüm: 2x 3y z 11 (I) x y 2z 7 (II) 3x 2y 3z 6 (III) II. denklemi ( ) ile çarpıp üç denklemi toplayalım; 2x 3y z 11 x y 2z 7 3x 2y 3z 6 4x 24 x 6 buluruz. 30 a b b c 8 a b c 39 ise, a kaçtır? A) 21 B)14 C) 13 D) 12 E) 11 www.matematikkolay.net Çözüm: a b b c 8 Burada iki eşitlik var, ayıralım. a b 8 her tarafın 2 katını alalım. 2a 2b 16 olur. b c 8 idi. a b c 39 idi. Üç denklemi taraf tarafa toplayalım. 3a 63 a 21 buluruz. 42 www.matematikkolay.net a.b 1 a b 4 b.c 1 b c 5 a.c 1 a c 6 olduğuna göre, c kaçtır? 7 2 2 A) 4 B) C) D) E) 8 2 5 7 www.matematikkolay.net 4 Çözüm: a.b 1 a b 4 tür. a b 4 a.b a b 1 1 4 4 a.b a.b b a b.c 1 b c 5 tir. b c 5 b.c b c 1 1 5 5 b.c b.c c b a.c 1 a c 6 tür. a c 6 a.c a c 1 1 6 6 a.c a.c c a 1 1 4 b a 1 1 5 c b 1 1 6 c a 1 1 1 1 1 1 15 2 15 dir a b c a b c 2 . 1 15 15 8 7 4 dir. c 2 2 2 1 7 2 c bulunur. c 2 7 www.matematikkolay.net 44 www.matematikkolay.net x y 1 xy 2 x z 1 xz 3 y z 1 olduğuna göre, z kaçtır ? yz 4 (6) (4) (3) Çözüm: x y 1 1 1 1 xy 2 y x 2 x z 1 1 1 1 xz 3 z x 3 y z 1 1 1 1 taraf tarafa topla. yz 4 z y 4 1 1 1 1 1 1 2 x y z 2 3 4 1 1 1 6 4 3 2 x y z 12 12 12 2 -12 01.Şub 1 1 1 13 x y z 12 1 1 1 13 1 13 1 dir. x y z 24 z 24 2 1 13 12 1 1 z 24 buluruz. z 24 z 24 49 3x y z 10 x 2y z 0 4x 3y 2z 16 denklem sisteminde y değeri kaçtır? A) 3 B) 2 C) 0 D) 1 E) 2 www.matematikkolay.net Çözüm: 2. ve 3. denklemi taraf tarafa toplayalım. 5x y z 16 olur. 1.denklemi bundan çıkaralım. 5x y z 16 _ 3x y z 10 2x 6 x 3 tür. İlk 2 denklemi taraf tarafa toplayınca; 3x y z 10 x 2y z 0 4x y 10 4. 3 y 10 12 y 10 y 2 buluruz. 51


1. SORUNUN ÇEVAĞPI YANLIŞ
Uyarınız için teşekkürler. Başka sorunun çözümü gelmiş oraya. Şimdi doğru çözüm konuldu.
Sitenizi çok seviyorum ve çok yararlı oluyor çok teşekkür ederim