Soru Sor sayfası kullanılarak 1.Dereceden Denklemler konusu altında Denklem Özellikleri ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

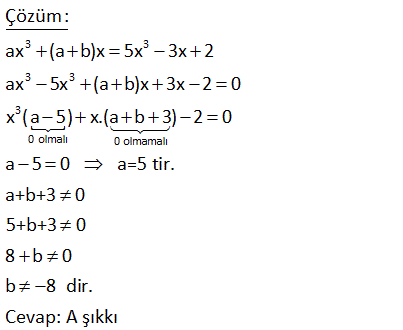
2.SORU


3.SORU


4.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
3 3 ax (a b)x 5x 3x 2 denklemi x değişkenine bağlı birinci dereceden bir bilinmeyenli bir denklem belirttiğine göre, b aşağıdakilerden hangisi olamaz? A) 8 B) 2 C) 2 D) 4 E) 8 www.matematikkolay.net 3 3 3 3 3 0 olmalı 0 olmamalı Çözüm: ax (a b)x 5x 3x 2 ax 5x (a b)x 3x 2 0 x (a 5) x.(a b 3) 2 0 a 5 0 a=5 tir. a+b+3 0 5+b+3 0 8 b 0 b 8 dir. Cevap: A şıkkı 18 3 2 1 A x 5 x 1 x 3 5 denkleminin köklerinden biri { 3,1,2,5} kümesinin bir elemanı olduğuna göre, A kaçtır? A) 6 B) 9 C) 12 D) 13 E) 16 www.matematikkolay.net 0 0 0 Çözüm: Rasyonel ifadelerde paydayı sıfır yapan değer çözüm olamaz.Şimdi paydaları sıfıra eşitleyip, denklemi sağlamayan x değerlerini bulalım. 3 2 1 A x 5 x 1 x 3 5 x 5 0 x 5 x 1 0 x 1 x 3 0 x 3 Buna göre de nklemin bir kökü bize verilen kümeden sadece 2 olabilir. x 2 için A değerini bulalım; 3 2 1 A 2 5 2 1 2 3 5 3 2 1 A A 1 1 2 3 1 5 5 5 5 A 1 1 A 1 5 A 6 buluruz. 5 19 2 2 (m 3)x (m 1)x m 1 0 denklemi x değişkenine bağlı birinci dereceden bir bilinmeyenli bir denklemdir. Buna göre, bu denklemi sağlayan x değeri kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 2 2 2 0 2 2 0 Çözüm: Denklem 1. dereceden olduğuna göre x li terimin katsayısı 0 olmalı. (m 3)x (m 1)x m 1 0 m 3 0 m 3 tür.Şimdi m değerini yerine yazalım. (3 3)x (3 1)x 3 1 0 8 4x 8 0 4x 8 x 2 buluruz. 4 www.matematikkolay.net 21 www.matematikkolay.net 2 b 3 (a 2)x 3x 13 0 ifadesi birinci dereceden bir bilinmeyenli denklem olduğuna göre, a b toplamı kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 2 b 3 Çözüm: Birinci dereceden ifadede x li bir terim olamaz. Dolayısıyla katsayısı 0 olmalıdır. a 2 0 a 2 dir. x ifadesinin üssü de 1 olmalıdır. b 3 1 b 2 dir. O halde; a b 2 ( 2) 0 buluruz. 46

