Soru Sor sayfası kullanılarak 1.Dereceden Denklemler konusu altında Çözüm Kümesi Sonsuz olursa ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

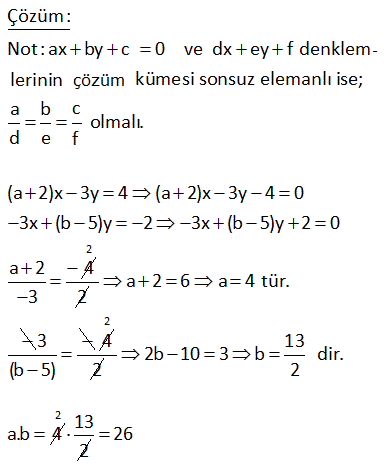
3.SORU


4.SORU

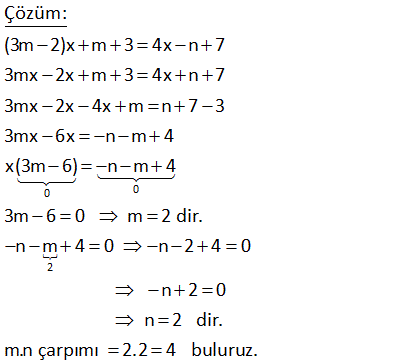
5.SORU

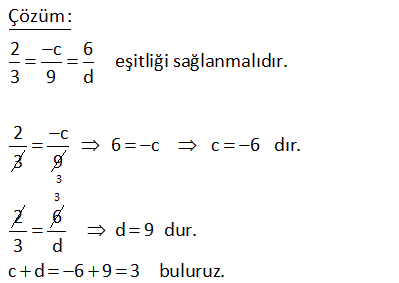
6.SORU


7.SORU

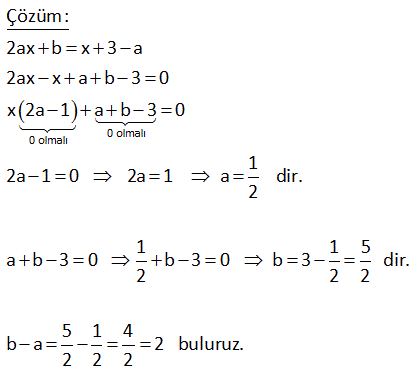
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
2 2 x değişkenine bağlı a x 16 25x b denkleminin çözüm kümesi sonsuz elemanlı oldua b ğuna göre, oranının alabileceği en büyük a b değer kaçtır? A) 1 B) 3 C) 4 D) 6 E) 9 www.matematikkolay.net 2 2 2 2 Çözüm: a x 16 25x b x’in katsayıları ve sabit terimler birbirine eşit olursa sonsuz çözüm olur. Buna göre; a 25 a 5 (en büyük dendiği için – 5’i almadık) b 16 b 4 a b 5 4 9 9 buluruz. a b 5 4 1 8 b (a 2)x 3y 4 3x (b 5)y 2 denklem sisteminin çözüm kümesi sonsuz elemanlı olduğuna göre, a kaçtır ? A) 4 B) 9 C) 13 D) 26 E) 29 www.matematikkolay.net Çözüm: Not : ax by c 0 ve dx ey f denklemlerinin çöüm kümesi sonsuz elemanlı ise; a b f olmalı. d e c (a 2)x 3y 4 (a 2)x 3y 4 0 3x (b 5)y 2 3x (b 5)y 2 0 a 2 4 3 2 2 a2 6a 4 tür. 3 (b 5) 4 2 2 13 2b 10 3 b dir. 2 Bu bulduğumuz değerlere göre bizce a.b sorulmak istenmiş. a.b 4 2 13 2 26 17 a(x 2) 3y 5 bx a(y 2) 7 denklem sistemini sağlayan sonsuz sayıda (x,y) ikilisi bulunduğuna göre, a’nın değerleri toplamı kaçtır? 1 3 5 A) B) C) 2 D) E) 2 2 2 2 www.matematikkolay.net x’in y’nin Sabit terim kats. kats. x’in y’nin Sabit terim kats. kats. Çözüm: a(x 2) 3y 5 ax 2a 3y 5 a x 3 y 5 2a (1.denklem) bx a(y 2) 7 bx ay 2a 7 b x a y 7 2a (2.denklem) Çözüm kümesinin sonsuz olması için, iki 2 2 denklemdeki tüm katsayıların oranları birbirine eşit olmalıdır. Yani; a 3 5 2a olmalıdır. b a 7 2a 3 5 2a (Burayı çözmeye çalışalım) a 7 2a 21 6a 5a 2a 0 2a a 21 dir. 1 1 Kökler toplamı bulu 2 2 ruz. 40 (3m 2)x m 3 4x n 7 denkleminin çözüm kümesi sonsuz elemanlı ise m.n çarpımı kaçtır? A) 1 B)2 C) 3 D) 4 E) 5 0 0 2 Çözüm: (3m 2)x m 3 4x n 7 3mx 2x m 3 4x n 7 3mx 2x 4x m n 7 3 3mx 6x n m 4 x(3m 6) n m 4 3m 6 0 m 2 dir. n m 4 0 n 2 4 0 n 2 0 n 2 dir. m.n çarpımı 2.2 4 buluruz. 45 2x yc 6 3x 9y d denklem sisteminin çözüm kümesi sonsuz elemanlı olduğuna göre, c d toplamı kaçtır? A) 1 B)2 C) 3 D) 5 E) 6 www.matematikkolay.net Çözüm: 2 c 6 eşitliği sağlanmalıdır. 3 9 d 2 3 c 9 3 6 c c 6 dır. 2 6 3 3 d 9 dur. d c d 6 9 3 buluruz. 52 denkleminin çözüm kümesi gerçek sayılar olduğuna gö 3 r x 1 x a e a b far kı kaçtı b r? 2 Çözüm: 3x 1 x a 2 b 3x 1 x a 2 2 b b x’lerin katsayıları birbirine eşit olmalıdır. 3 1 2 b tür. 2 b 3 Sabit terimler de birbirine eşit olmalıdır. 1 a 1 a 1 2 b 2 2 2 3 3a 2 1 a 3 1 2 3 O halde; a b 1 buluruz. 3 3 3 56 a ve b birer gerçek sayıdır. 2ax b x 3 a denkleminin her x gerçek sayısı için sonsuz sayıda çözümü olduğuna göre b a farkı kaçtır? A) 4 B) 1 C) 2 D) 7 E) 10 www.matematikkolay.net 0 olmalı 0 olmalı Çözüm: 2ax b x 3 a 2ax x a b 3 0 x 2a 1 a b 3 0 1 2a 1 0 2a 1 a dir. 2 1 1 5 a b 3 0 b 3 0 b 3 dir. 2 2 2 5 1 4 b a 2 buluruz. 2 2 2


elinize sağlık hocam
2.Sorunun çözüm bölümünde f/c yazılmış, c/f olması gerekiyor.
Uyarınız için teşekkürler. Düzeltildi.