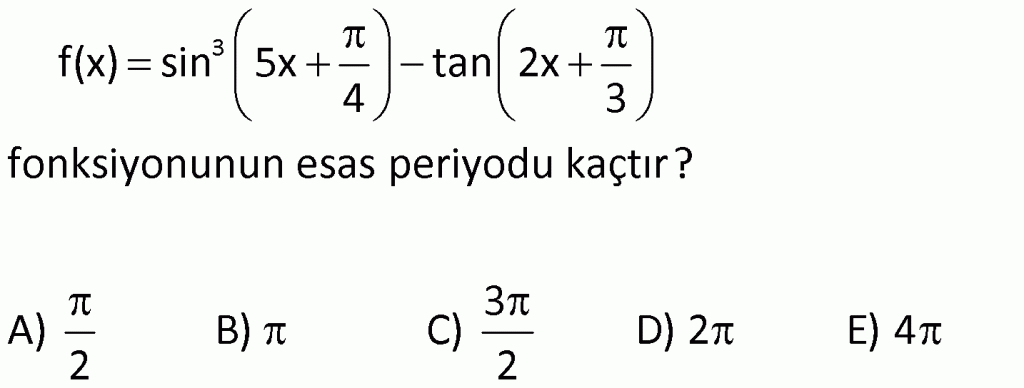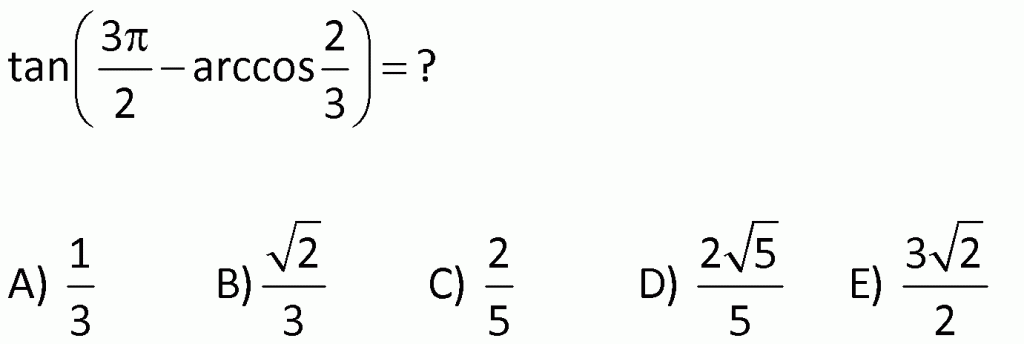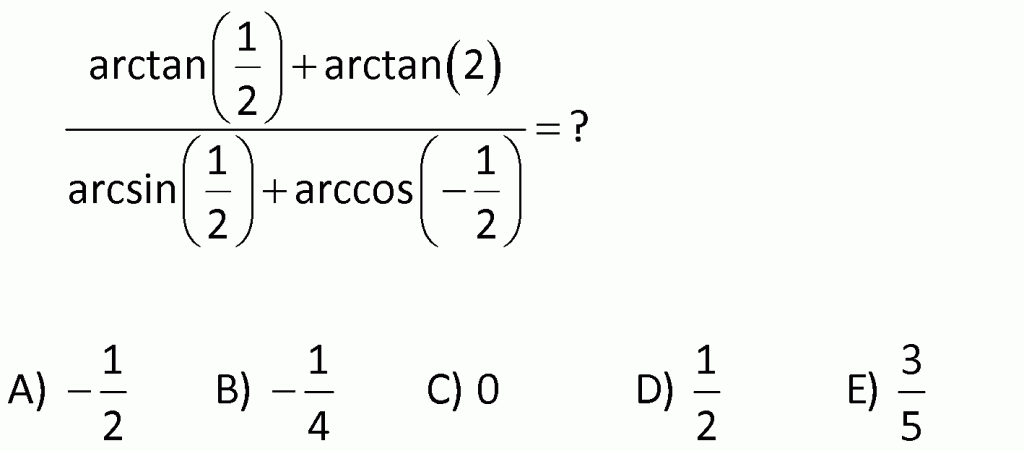Trigonometri Konu Anlatımı (11.Sınıf)

3.Sayfaya Dönmek için Tıklayınız.

TRİGONOMETRİK FONKSİYONLARIN PERİYOTLARI

Kosinüs ve Sinüs’ün Esas Periyodu

$\displaystyle {{\cos }^{n}}(ax+b)$ ve $\displaystyle {{\sin }^{n}}(ax+b)$ fonksiyonlarının esas periyodu

n tek ise $\displaystyle \frac{{2\pi }}{{\left| a \right|}}$

n çift ise $\displaystyle \frac{{\pi }}{{\left| a \right|}}$ dir.

Örnek: $\displaystyle {{\cos }^{3}}(5x+22{}^\circ )$ nin esas periyodu kaçtır?

Çözüm

$\displaystyle T=\frac{{2\pi }}{5}$ tir.

Örnek: $\displaystyle {{\sin }^{4}}\left( {\frac{\pi }{2}-\frac{x}{5}} \right)$ in esas periyodu kaçtır?

Çözüm

x in katsayısı -1/5 tir. Mutlak olarak ise 1/5 tir. Ayrıca sinüs’ün çift kuvveti alınıyor. Dolayısıyla

$\displaystyle T=\frac{\pi }{{\frac{1}{5}}}=5\pi$ dir.

Tanjant ve Kotanjant’ın Esas Periyodu

$\displaystyle {{\tan }^{n}}(ax+b)$ ve $\displaystyle {{\cot }^{n}}(ax+b)$ fonksiyonlarının esas periyodu

$\displaystyle T=\frac{\pi }{{\left| a \right|}}$ dır.

Örnek: $\displaystyle {{\tan }^{5}}(-3x+5)$ in esas periyodu kaçtır?

Çözüm

$\displaystyle T=\frac{\pi }{3}$ tür.

$f(x)=g(x)\pm h(x)$ fonksiyonlarının esas periyodu, EKOK’larına eşittir.

Hatırlatma: Kesirler en sade biçimde olmak üzere,

$\displaystyle EKOK\left( {\frac{a}{b},\text{ }\frac{c}{d}} \right)=\frac{{EKOK\left( {a,c} \right)}}{{EBOB(b,d)}}$ dir.

Alıştırma 18

Çözüm

TRİGONOMETRİK FONKSİYONLARIN GRAFİKLERİ

Çizmek için,

Fonksiyonun esas periyodu bulunur.
Bu periyotta bazı değerler için örnek değerler elde edilir. Fonksiyonun artışa geçtiği veya azaldığı yerler anlamaya çalışılır.
Bulunan değerlere göre uygun bir grafik çizilmeye çalışılır. Periyotlar boyunca grafik tekrar edilir.

Trigonometrik grafikler, tam anlamıyla bilgisayarlar tarafından çizilebilir. Bizden istenen yaklaşık olarak grafiğini çizebilmek ve buna dayalı olarak grafiklerini yorumlayabilmek.

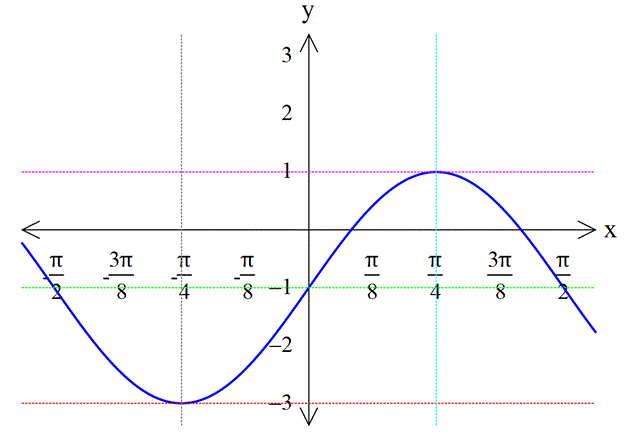
SİNÜS FONKSİYONUNUN GRAFİĞİ

$\displaystyle f:\text{ }\mathbb{R}\to [-1,1],\text{ }f(x)=\sin x$

fonksiyonunun grafiği aşağıda çizilmiştir.

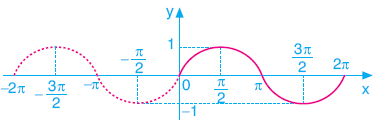
Sinüs fonksiyonu orjine göre simetrik olduğu için tek fonksiyondur. Yani

sin(-x)=-sinx tir.

KOSİNÜS FONKSİYONUNUN GRAFİĞİ

$f:\text{ }\mathbb{R}\to [-1,1],\text{ }f(x)=\cos x$

fonksiyonunun grafiği aşağıda çizilmiştir.

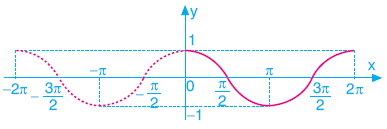
Kosinüs fonksiyonu y eksenine göre simetrik olduğu için çift fonksiyondur. Yani

cos(-x)=cosx tir.

Tanım kümelerini aşağıdaki gibi daraltırsak, birebir ve örten fonksiyonlar elde ederiz (Ters fonksiyonunun olabilmesi için bu daraltmaya ihtiyacımız olacak).

$f:\text{ }\left[ {-\frac{\pi }{2}\text{ },\text{ }\frac{\pi }{2}} \right]\to \left[ {-1,\text{ }1} \right],\text{ }f(x)=\sin x\text{ }fonksiyonu\text{ }bire\text{ }bir\text{ }ve\text{ }\ddot{o}rtendir.$

$\displaystyle f:\text{ }\left[ {0\text{ },\text{ }\pi } \right]\to \left[ {-1,\text{ }1} \right],\text{ }f(x)=\cos x\text{ }fonksiyonu\text{ }bire\text{ }bir\text{ }ve\text{ }\ddot{o}rtendir.$

TANJANT FONKSİYONUNUN GRAFİĞİ

$\left[ {-\frac{\pi }{2}\text{ },\text{ }\frac{\pi }{2}} \right]\text{ aral }\!\!\imath\!\!\text{ }\!\!\breve{\mathrm{g}}\!\!\text{ }\!\!\imath\!\!\text{ nda}\text{, }f(x)=\tan x\text{ }$ fonksiyonunun grafiği çizilmiştir.

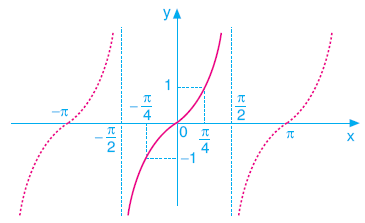
$\displaystyle \frac{\pi }{2}$ nin tek katlarında tanımsız olduğuna dikkat ediniz.

Tanjant fonksiyonu orjine göre simetrik olduğu için tek fonksiyondur. Yani

tan(-x)=-tanx tir.

KOTANJANT FONKSİYONUNUN GRAFİĞİ

$\left[ {0,\text{ }\pi } \right]\text{ aral }\!\!\imath\!\!\text{ }\!\!\breve{\mathrm{g}}\!\!\text{ }\!\!\imath\!\!\text{ nda}\text{, }f(x)=\cot x\text{ }$ fonksiyonunun grafiği olarak çizilmiştir.

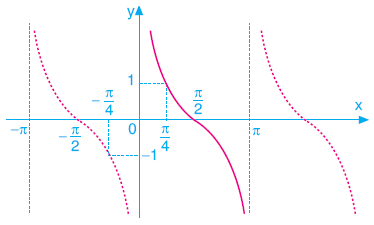
$\displaystyle \pi$ nin katlarında tanımsız olduğuna dikkat ediniz.

Kotanjant fonksiyonu orjine göre simetrik olduğu için tek fonksiyondur. Yani

cot(-x)=-cotx tir.

Tanım kümelerini aşağıdaki gibi daraltırsak, birebir ve örten fonksiyonlar elde ederiz (Ters fonksiyonunun olabilmesi için bu daraltmaya ihtiyacımız olacak).

$f:\text{ }\left[ {-\frac{\pi }{2}\text{ },\text{ }\frac{\pi }{2}} \right]\to \mathbb{R},\text{ }f(x)=\tan x\text{ }fonksiyonu\text{ }bire\text{ }bir\text{ }ve\text{ }\ddot{o}rtendir.$

$\displaystyle f:\text{ }\left[ {0\text{ },\text{ }\pi } \right]\to \mathbb{R},\text{ }f(x)=\cot x\text{ }fonksiyonu\text{ }bire\text{ }bir\text{ }ve\text{ }\ddot{o}rtendir.$

Alıştırma 19

Çözüm

TERS TRİGONOMETRİK FONKSİYONLAR

ARKSİNÜS FONKSİYONU

Tanım aralığı $\left[ {-\frac{\pi }{2}\text{ },\text{ }\frac{\pi }{2}} \right]$ alınmış sinx fonksiyonunun tersine arcsinx denir.

$\arcsin x:\text{ }[-1,1]\to \left[ {-\frac{\pi }{2}\text{ },\text{ }\frac{\pi }{2}} \right]\text{ }dir.$

Örnek: $\displaystyle \arcsin \left( {\frac{1}{2}} \right)=30{}^\circ$ dir. Çünkü sinüsü 1/2 olan açı 30 derecedir.

Örnek: $\displaystyle \arcsin \left( {-\frac{1}{2}} \right)=-30{}^\circ$ dir. Çünkü sinüsü -1/2 olan açı -30 derecedir.

Dikkat: arcsinüs’ün eşit olduğu açılar $\displaystyle [-90,\text{ 90}]$ yani $\displaystyle \left[ {-\frac{\pi }{2},\text{ }\frac{\pi }{2}} \right]$ aralığındadır.

Örnek: $\displaystyle \tan \left( {\arcsin \left( {\frac{1}{3}} \right)} \right)$ =?

Çözüm

Sinüsü $\displaystyle {\frac{1}{3}}$ olan açı x açısı olsun ve bunu dik üçgende çizelim.

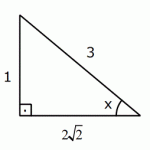
$\displaystyle \tan \underbrace{{\left( {\arcsin \left( {\frac{1}{3}} \right)} \right)}}_{x}=\tan x=\underset{{\left( {\sqrt{2}} \right)}}{\mathop{{\frac{1}{{2\sqrt{2}}}}}}\,=\frac{{\sqrt{2}}}{4}$ tür.

ARKKOSİNÜS FONKSİYONU

Tanım aralığı $\left[ {0\text{ },\text{ }\pi } \right]$ alınmış cosx fonksiyonunun tersine arccosx denir.

Bu durumda,

$\arccos x:\text{ }[-1,1]\to \left[ {0,\text{ }\pi } \right]\text{ }dir.$

Örnek: $\displaystyle \arccos 0=\frac{\pi }{2}$ dir. Çünkü $\displaystyle [0,\text{ }\pi ]$ aralığında kosinüsü 0 olan açı $\displaystyle \frac{\pi }{2}$ dir.

Örnek: $\displaystyle \arccos \left( {-\frac{1}{2}} \right)$ = $\displaystyle \frac{{2\pi }}{3}$ tür. Çünkü $\displaystyle [0,\text{ }\pi ]$ aralığında kosinüsü $\displaystyle {-\frac{1}{2}}$ olan açı $\displaystyle \frac{{2\pi }}{3}$ tür.

Alıştırma 20

Çözüm

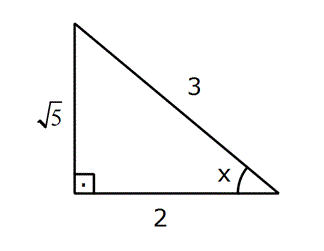
ARKTANJANT FONKSİYONU

Tanım aralığı $\left( {-\frac{\pi }{2}\text{ },\text{ }\frac{\pi }{2}} \right)$ alınmış tanx fonksiyonunun tersine arctanx denir.

Bu durumda,

$\arctan x:\text{ }\mathbb{R}\to \left( {-\frac{\pi }{2}\text{ },\text{ }\frac{\pi }{2}} \right)\text{ }dir.$

Örnek: $\arctan \left( {\sqrt{3}} \right)=\frac{\pi }{3}$ tür.

Örnek: $\arctan \left( {-\sqrt{3}} \right)=-\frac{\pi }{3}$ tür.

ARKKOTANJANT FONKSİYONU

Tanım aralığı $\left( {0\text{ },\text{ }\pi } \right)$ alınmış cotx fonksiyonunun tersine arccotx denir.

Bu durumda,

$\text{arccotx}:\text{ }R\to (0,\text{ }\pi )$

Örnek: $\arccot \left( 1 \right)=\frac{\pi }{4}$ tür.

Örnek: $\arccot \left( {-1} \right)=\frac{{3\pi }}{4}$ tür.

Alıştırma 21

Çözüm

Not: Bir fonksiyonun ters fonksiyonunun ters fonksiyonu fonksiyonun kendisine eşittir.

sin(arcsinx) = x tir.

cos(arccosx) = x tir.

tan(arctanx) = x tir.

cot(arccotx) = x tir.

Çözümlü Sorular veya Çıkmış Sorular için Tıklayın.

Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)

Sayfalar: 1 2 3 4