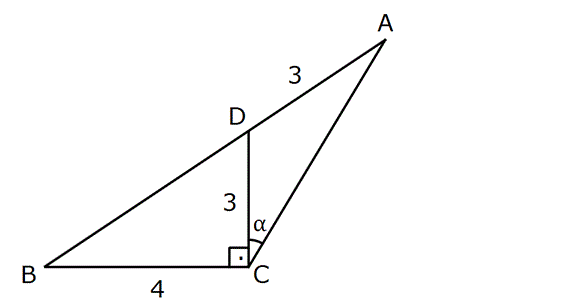
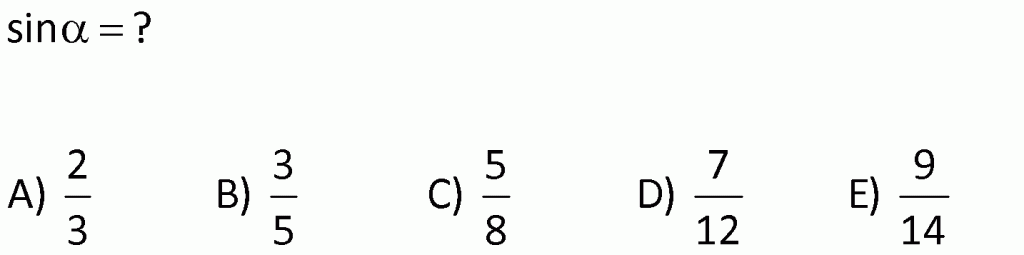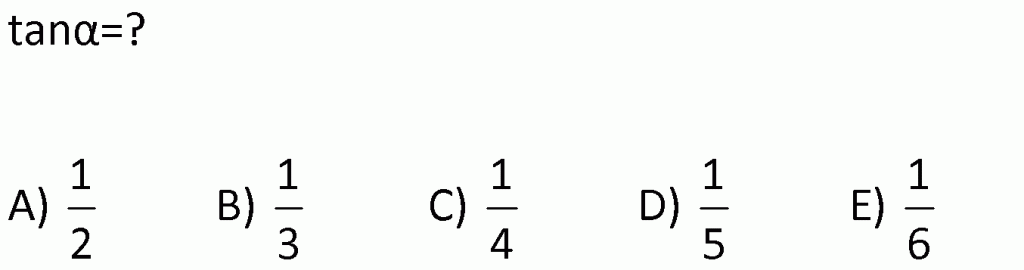Trigonometri Konu Anlatımı (11.Sınıf)

ÜÇGENDE TRİGONOMETRİK BAĞINTILAR

Kosinüs Teoremi

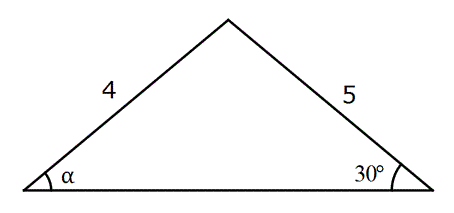
Bir üçgende iki kenar ve arasındaki açıyı bilerek, karşıdaki kenarı Kosinüs Teoremi ile hesaplayabiliriz.

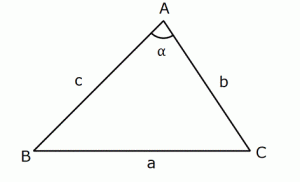
$\displaystyle {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc.\cos \alpha$ dır.

Örnek:

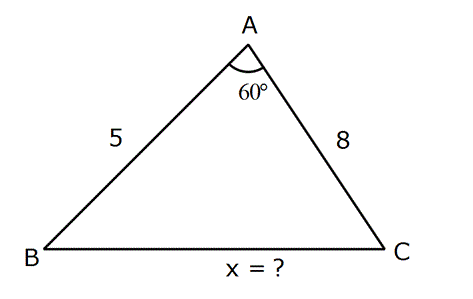
Çözüm

$\displaystyle {{x}^{2}}={{5}^{2}}+{{8}^{2}}-2.5.8.\cos 60$

$\displaystyle {{x}^{2}}=25+64-\cancel{2}.5.8\cdot \frac{1}{{\cancel{2}}}$

$\displaystyle {{x}^{2}}=89-40$

$\displaystyle {{x}^{2}}=49$

$\displaystyle x=7$ buluruz.

Alıştırma 13

Çözüm

Alıştırma 14

Çözüm

Alıştırma 15

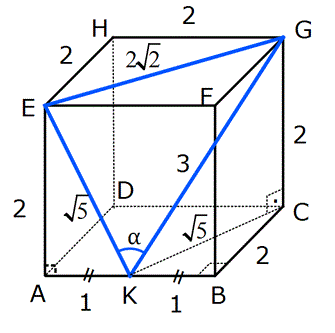
Çözüm

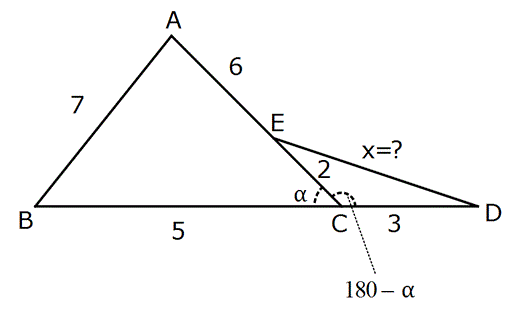
Sinüs Teoremi

Bir üçgende kenar ile karşısındaki açının sinüsü arasında doğru orantı vardır. Bu oran da çevrel çemberin yarıçapının 2 katıdır.

$\displaystyle \frac{a}{{\sin A}}=\frac{b}{{\sin B}}=\frac{c}{{\sin C}}=2R$ dir.

Alıştırma 16

Çözüm

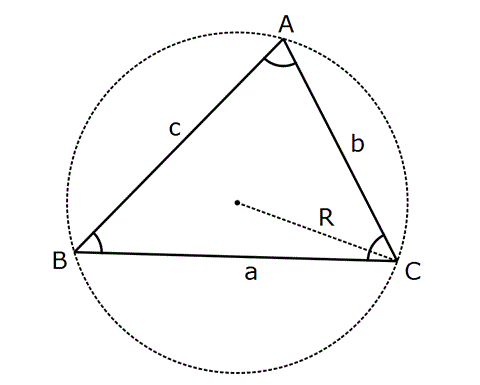
Alıştırma 17

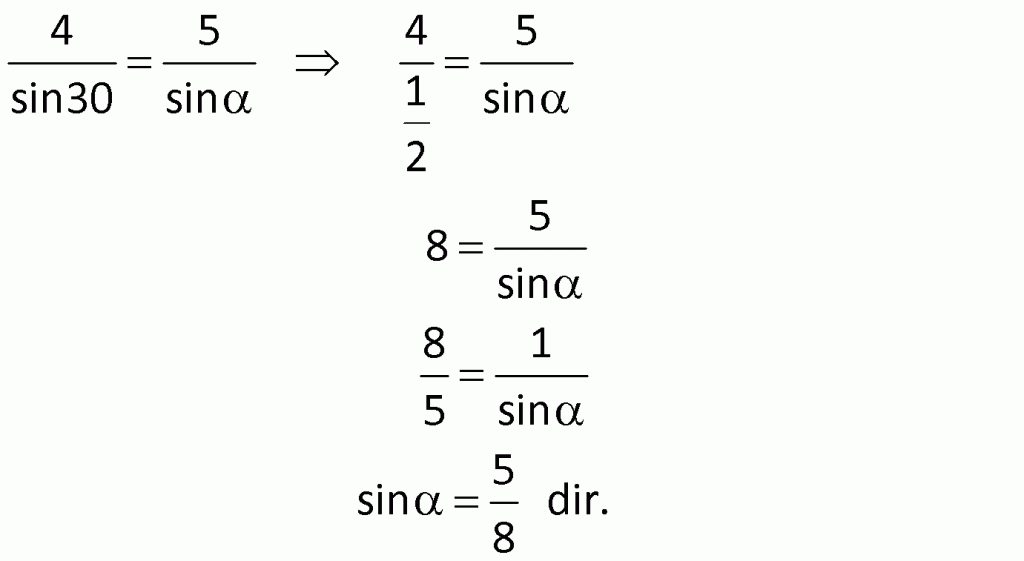
Çözüm

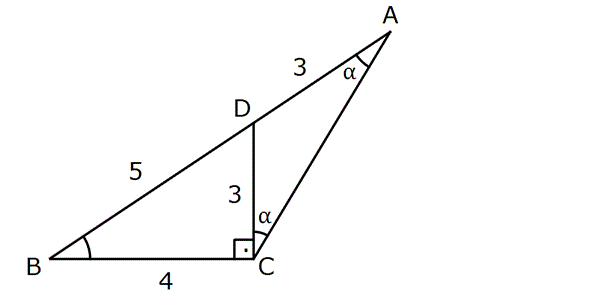
Hatırlatma:

1) Sinüslü Alan Formülü

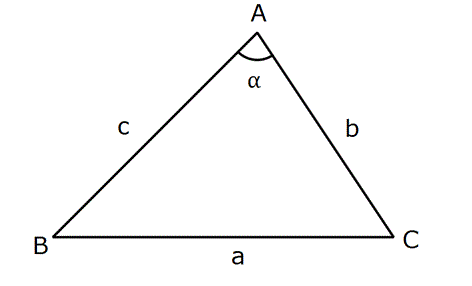
$\displaystyle A(ABC)=\frac{1}{2}\cdot b.c.\sin \alpha$ dır.

2) u’lu alan Formülü

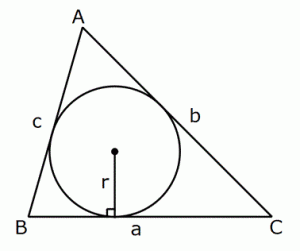
u=çevrenin yarısı ve r=iç teğet çemberinin yarıçapı olmak üzere,

Alan(ABC)=u.r dir.

3) Çevrel Çember ile Alan Bulma

$\displaystyle A(ABC)=\frac{{a.b.c}}{{4R}}$ dir.

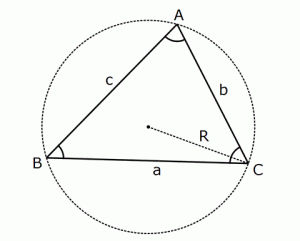
Sayfalar: 1 2 3 4