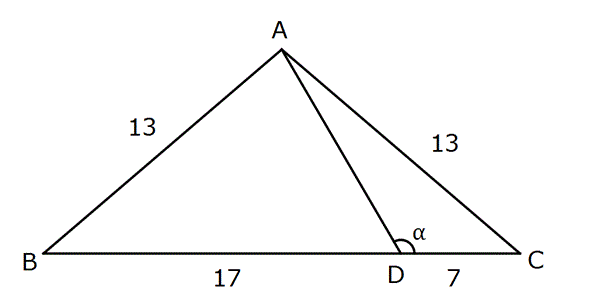
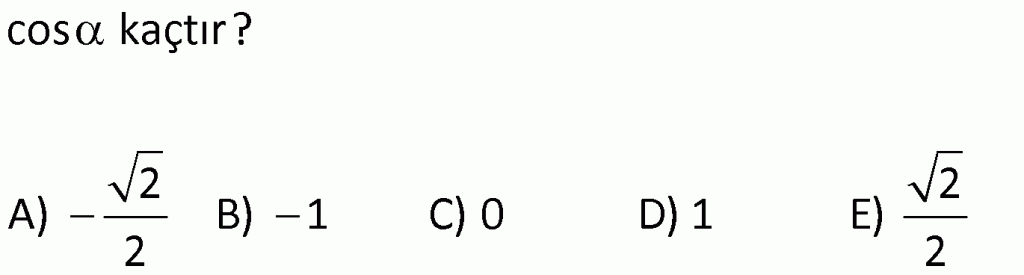GENİŞ AÇILARIN TRİGONOMETRİK ORANLARI (DAR AÇIYA İNDİRGEME)
İlk verilen açı, esas ölçü dışında ise esas ölçüsü alınır.
x açısının dar açı olduğu kabul edilerek trigonometrik oranın işaret tespiti yapılır. Eğer negatifse, başa – işareti konacaktır.
![]() ya da
ya da ![]() nin tek katlarında sinüs ile kosinüs, tanjant ile kotanjant yer değiştirir.
nin tek katlarında sinüs ile kosinüs, tanjant ile kotanjant yer değiştirir.
![]() ya da
ya da ![]() nin çift katlarında fonksiyonların adı aynı olur.
nin çift katlarında fonksiyonların adı aynı olur.
Örnek: cos(90+x)=?
90+x açısı 2.bölgededir. 2.bölgede kosinüs (-) dir. Dolayısıyla başa (-) işareti gelecektir.
90 açısı da 90’ın 1 katıdır(tek katı). Dolayısıyla kosinüs, sinüse dönüşecektir. O halde,
cos(90+x)=-sinx tir.
Örnek: tan(180+x)=?
180+x açısı 3.bölgededir. 3.bölgede tanjant (+) dır.
180 açısı da 90’ın 2 katıdır(çift katı). Dolayısıyla fonksiyonun adı değişmeyecektir. O halde,
tan(180+x)=tanx tir.
Örnek: cos(210)=?
Çözüm
210=180+30 olarak düşünebiliriz. 180+x açısı 3.bölgededir. 3.bölgede kosinüs (-) dir.
180 açısı da 90’ın 2 katıdır(çift katı). Dolayısıyla fonksiyonun adı değişmeyecektir. O halde,
cos(180+30)=-cos30 dur. ![]() olduğundan, cevap
olduğundan, cevap ![]() dir.
dir.
Örnek: ![]()
Çözüm
![]() açısı 4.bölgededir. 4.bölgede tanjant (-) dir.
açısı 4.bölgededir. 4.bölgede tanjant (-) dir.
![]() açısı da
açısı da ![]() ‘nin 4 katıdır(çift katı). Dolayısıyla fonksiyonun adı değişmeyecektir. O halde,
‘nin 4 katıdır(çift katı). Dolayısıyla fonksiyonun adı değişmeyecektir. O halde,
![]() dır.
dır.
Örnek: ![]()
Çözüm
![]() ün esas ölçüsünü bulalım. Paydanın 2 katı 8 dir. 21’in 8’e bölümünden kalan 5 tir. O halde
ün esas ölçüsünü bulalım. Paydanın 2 katı 8 dir. 21’in 8’e bölümünden kalan 5 tir. O halde ![]() ü bulacağız.
ü bulacağız.
![]() olarak yazabiliriz.
olarak yazabiliriz. ![]() açısı 3.bölgededir. Bu bölgede sinüs (-) dir.
açısı 3.bölgededir. Bu bölgede sinüs (-) dir.
![]() açısı
açısı ![]() nin çift katı olduğundan fonksiyonun adı değişmez. O halde, –
nin çift katı olduğundan fonksiyonun adı değişmez. O halde, –![]() ü elde ederiz. O da –
ü elde ederiz. O da –![]() dir.
dir.
Not: Sadece ![]() eşittir. Diğerleri (
eşittir. Diğerleri (![]() ) eksilisine (-) eşittir.
) eksilisine (-) eşittir.
Örnek: ![]()
Çözüm
![]() dir.
dir.
Çözüm
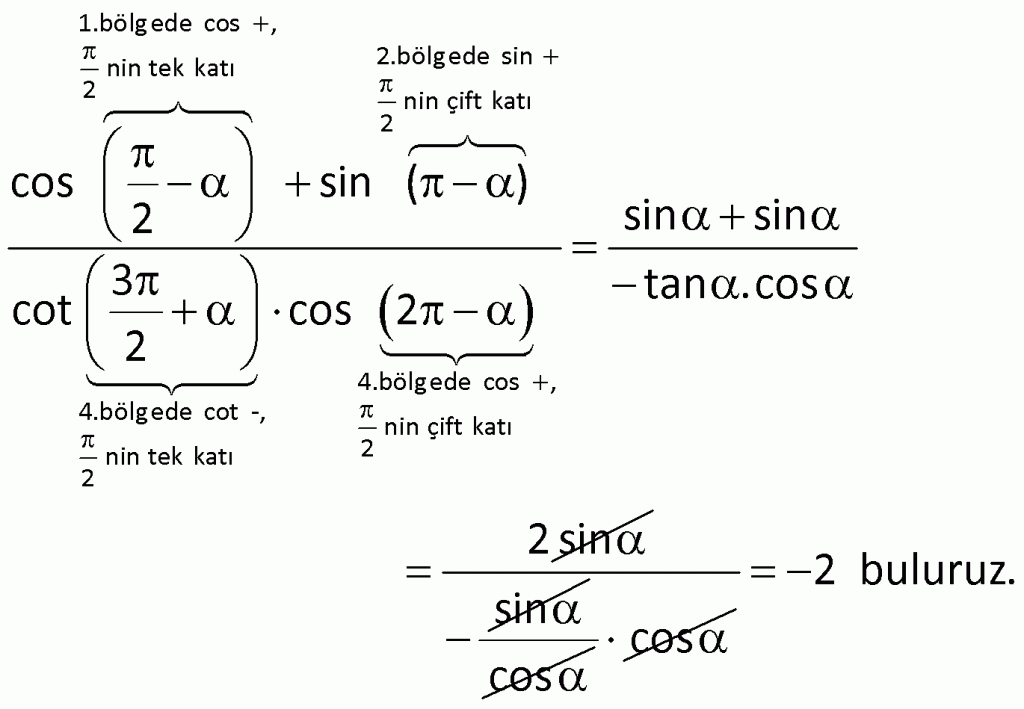
Not: ![]() ise
ise ![]() ve
ve ![]() dir.
dir.
Örnek: tan17=cot73, sin12=cos78, ![]()
Çözüm

Çözüm
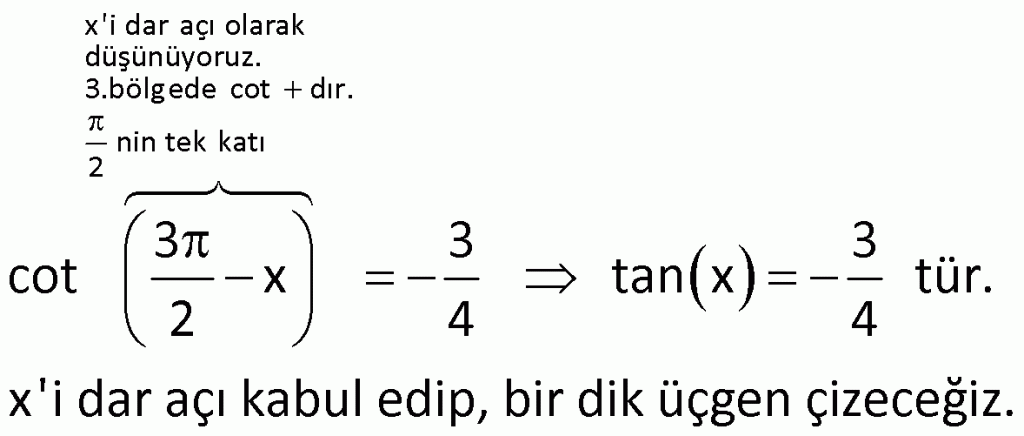
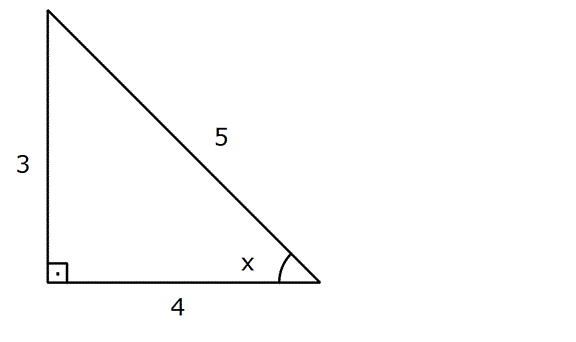
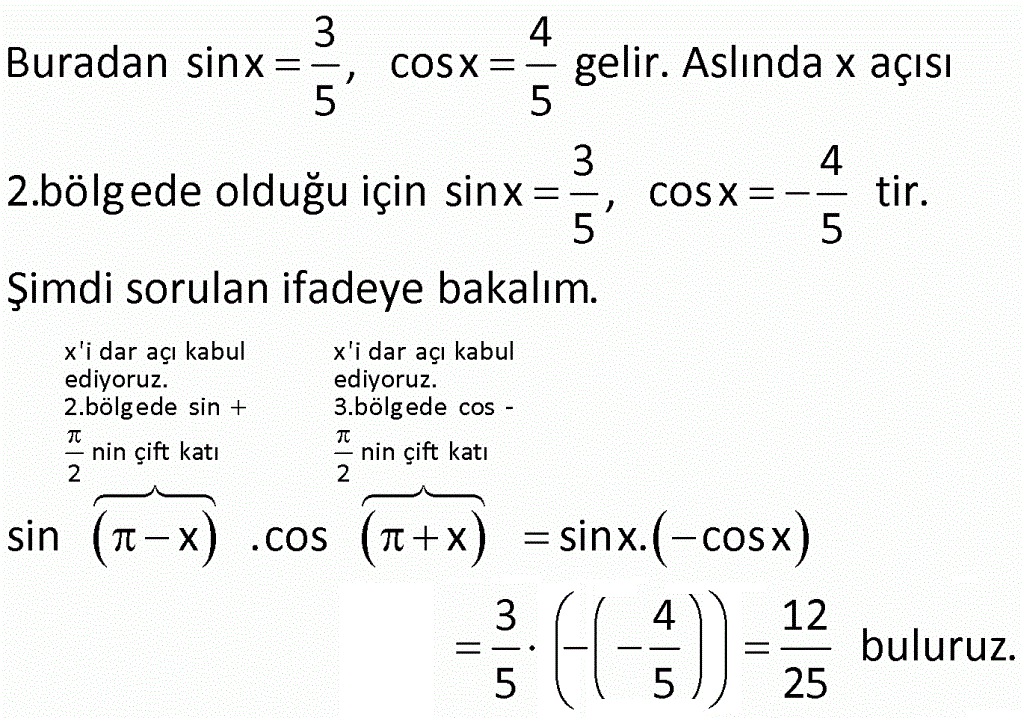
Çözüm