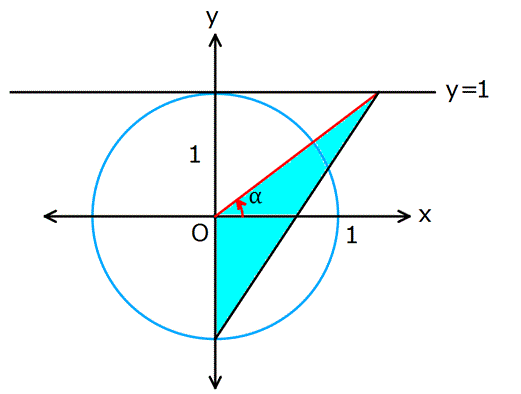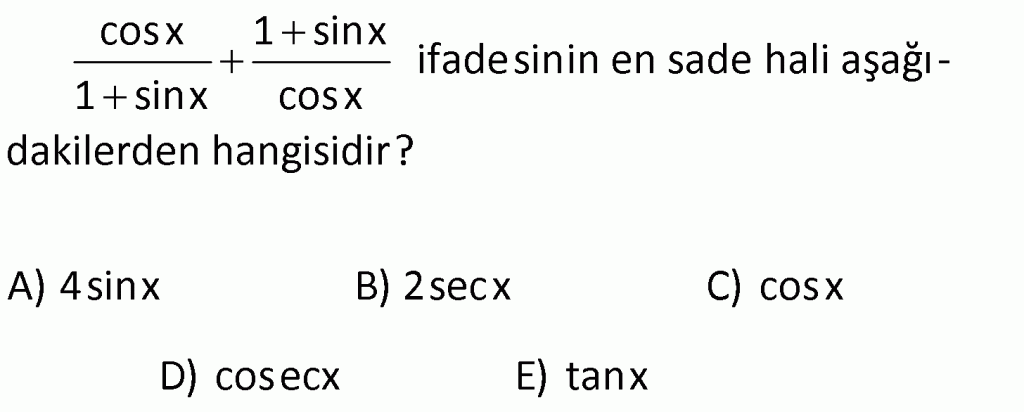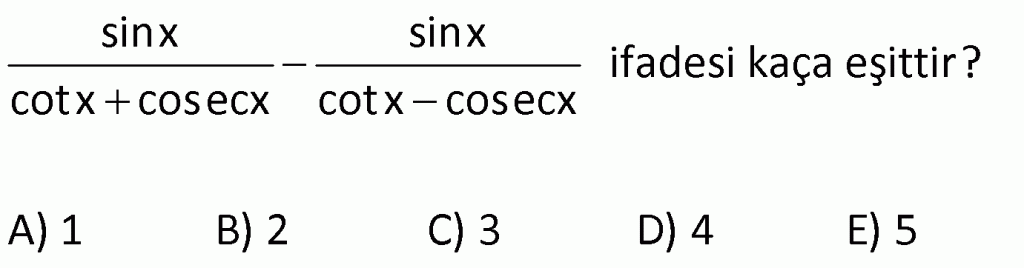YÖNLÜ AÇI
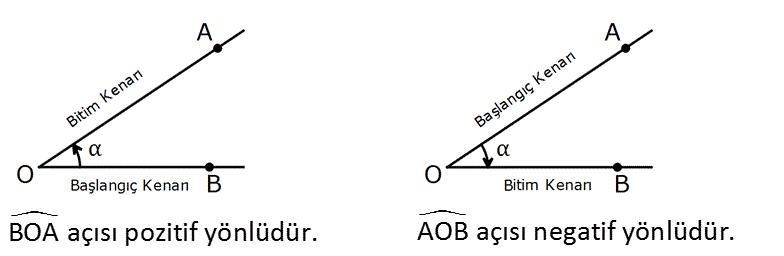
Bir açının kenarları, başlangıç ve bitim şeklinde belirtilirse bu açı yönlü açı olur.
Saat yönündeki açı negatif açıdır, tersi yönündeki açı da pozitiftir.
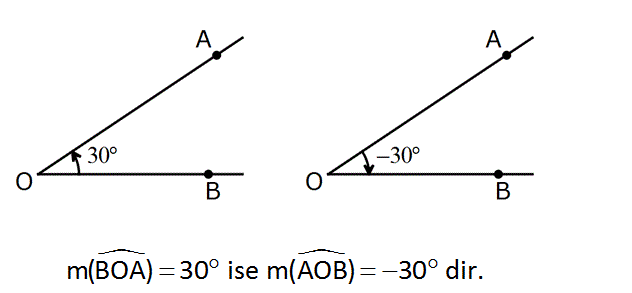
Örnek:
AÇI ÖLÇÜ BİRİMLERİ
Açı ölçü birimi olarak sıklıkla derece ve radyan kullanılır.
Derece
Bir tam çember yayının 360 eş parçasından birini gören merkez açıya 1 derece denir ve 1° ile gösterilir. Dolayısıyla tam açı 360° dir.
Dereceden de küçük açıları ifade etmek için dakika ve saniye kullanılır.
1° nin 1/60 ına 1 dakika denir ve 1′ ile gösterilir.
1′ nin 1/60 ına da 1 saniye denir ve 1” ile gösterilir.
Örnek: 3600 saniye kaç derecedir?
İlk önce kaç dakika olduğunu bulalım. 3600/60=60 dakikadır.
Sonra kaç derece olduğunu bulalım. 60/60=1 derecedir.
Örnek: 15159 saniye kaç derece, kaç dakika, kaç saniyedir?
Çözüm için Tıklayınız.

Örnek: 1,12° kaç saniyedir?
Çözüm
1 derece 3600 saniye ise,
1,12 x 3600=112 x 36 = 4032 saniyedir.
Çözüm

Radyan
Bir çemberde yarıçap kadar yay gören merkez açıya 1 radyan denir.
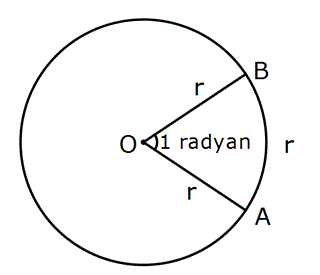
Tam açı ![]() radyan dır. O halde, 360° =
radyan dır. O halde, 360° = ![]() radyan dır. Buna dayanarak şu formülü üretebiliriz:
radyan dır. Buna dayanarak şu formülü üretebiliriz:
![]()
Örnek: 45° kaç radyandır?
Çözüm
![]() radyandır.
radyandır.
Not: Radyandan dereceye geçiş yaparken, ![]() yerine 180° yazmak yeterlidir.
yerine 180° yazmak yeterlidir.
Örnek: ![]() radyan kaç derecedir?
radyan kaç derecedir?
Çözüm
![]() dir.
dir.
ESAS ÖLÇÜ
Açıların, birim çember üzerinde denk geldikleri açıya esas ölçü denir.
Esas ölçü ![]() aralığında ifade edilir. Radyan olarak ise
aralığında ifade edilir. Radyan olarak ise ![]() aralığında ifade edilir.
aralığında ifade edilir.
Esas ölçü daima pozitif yönlüdür. Negatif esas ölçü olamaz.
Esas Ölçü Hesaplama
Derece pozitif olarak verilmişse, açı 360° ye bölünür. Kalan açı esas ölçüdür.
Örnek: 750° nin esas ölçüsü nedir?
Çözüm
![]() Esas ölçüsü 30° dir.
Esas ölçüsü 30° dir.
Derece negatif olarak verilmişse, açı pozitifmiş gibi 360° ye bölünür. Kalan açı 360° den çıkarılarak esas ölçü bulunur.
Örnek: -570° nin esas ölçüsü nedir?
Çözüm
I.Yol:
Açıyı pozitif 570° gibi düşünelim. 570’in 360’a bölümünden kalan 210 dur.
Bunu da 360 tan çıkartırsak, 360-210=150° buluruz.
II.Yol:
![]() şeklinde yazarak
şeklinde yazarak
![]() Esas ölçü 150° dir.
Esas ölçü 150° dir.
Açı, radyan olarak verilmişse bu sefer ![]() den kalana bakılır. Negatif ise, kalan
den kalana bakılır. Negatif ise, kalan ![]() den çıkarılır.
den çıkarılır.
Örnek: ![]() ile
ile ![]() nin esas ölçüleri arasındaki fark nedir?
nin esas ölçüleri arasındaki fark nedir?
Çözüm
21’in 2’ye bölümünden kalan 1 dir. Dolayısıyla ![]() nin esas ölçüsü
nin esas ölçüsü ![]() dir.
dir.
15’in 2’ye bölümünden kalan 1 dir. Açı negatif olduğu için, ![]() den
den ![]() yi çıkarırız.
yi çıkarırız. ![]() olur. Bunun da esas ölçüsü
olur. Bunun da esas ölçüsü ![]() oldu.
oldu.
İkisi arasındaki fark ![]() –
–![]() =0 dır.
=0 dır.
Eğer radyan açı kesirli olarak verilmişse, paydaki sayı paydanın 2 katına bölünür. Kalan sayı ![]() nin katsayısı olarak yazılınca bu kesir esas ölçüsü olur. Eğer açı negatif ise, bu kesir
nin katsayısı olarak yazılınca bu kesir esas ölçüsü olur. Eğer açı negatif ise, bu kesir ![]() den çıkarılarak esas ölçü bulunur.
den çıkarılarak esas ölçü bulunur.
Örnek: ![]() ün esas ölçüsü nedir?
ün esas ölçüsü nedir?
Çözüm
Paydanın 2 katı 6 dır. 14’ün 6’ya bölümünden kalan 2 dir.
O halde esas ölçüsü ![]() tür.
tür.
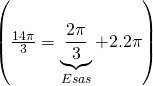
Örnek: ![]() ün esas ölçüsü nedir?
ün esas ölçüsü nedir?
Çözüm
Paydanın 2 katı 8 dir. 23’ün 8’e bölümünden kalan 7 dir.
Şimdi ![]() kesrini elde ettik. Ancak, açı negatif olduğu için bunu
kesrini elde ettik. Ancak, açı negatif olduğu için bunu ![]() den çıkarmalıyız.
den çıkarmalıyız.
![]() buluruz.
buluruz.
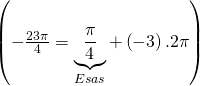
TRİGONOMETRİK FONKSİYONLAR
Kosinüs ve Sinüs Fonksiyonları
Bir dik üçgende, komşu dik kenarın hipotenüse oranı sinüs idi. Birim çember üzerinde ise, apsis (x) değeridir(Birim çemberin yarıçapı 1 olduğu için).
Sinüs ise, bir dik üçgende karşı dik kenarın hipotenüse oranı idi. Birim çemberde ise, ordinat (y) değeridir.
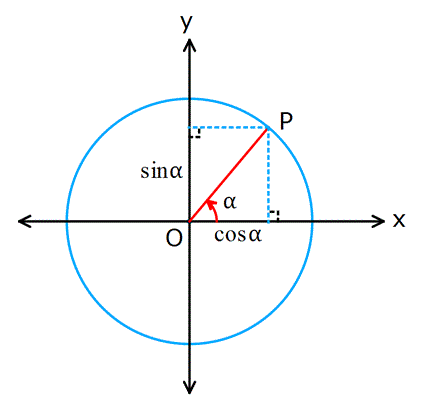
P(![]() ) olarak ifade edebiliriz.
) olarak ifade edebiliriz.
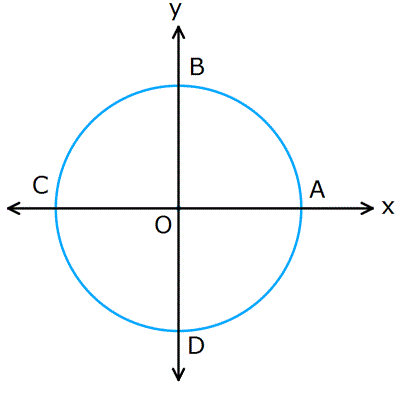
A noktasının koordinatları (cos0, sin0)=(1, 0) dır.
B noktasının koordinatları (cos90, sin90)=(0, 1) dir.
C noktasının koordinatları (cos180, sin180)=(-1, 0) dir.
D noktasının koordinatları (cos270, sin270)=(0, -1) dir.
Hem kosinüs hem de sinüs fonksiyonu [-1, 1] kapalı aralığında değer alabilir. Bunun dışına çıkamazlar. Dolayısıyla en küçük değerleri -1, en büyük değerleri de 1 dir, diyebiliriz.
Örnek: f(x)=3cosx+2 fonksiyonunun görüntü kümesini bulunuz.
Çözüm
cosx en az -1 olabilir. Dolayısıyla en küçük f(x)=3(-1)+2=-3+2=-1 dir.
cosx en fazla 1 olabilir. Dolayısıyla en büyük f(x)=3.1+2=3+2=5 tir. O halde,
Görüntü kümesi: [-1, 5] aralığıdır.
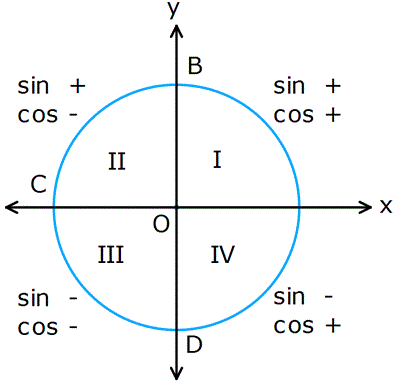
Bölgelere göre, sinüs ve kosinüsün işareti
Çözüm

Tanjant Fonksiyonu
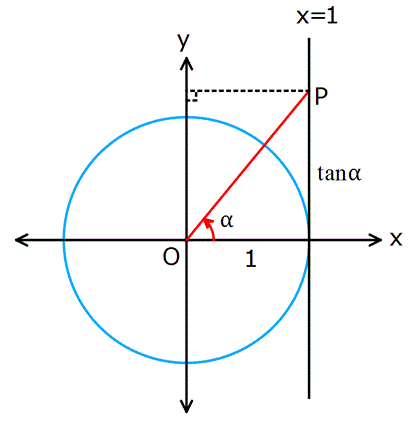
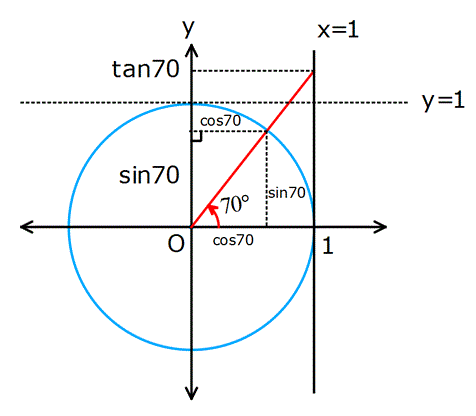
Dik üçgende, karşı dik kenarın komşu dik kenara oranı bize tanjantı veriyordu.
Birim çemberde ise, açının x=1 doğrusu üzerinde kestiği noktanın ordinatıdır(Komşu dik kenar 1 birim olduğu için).
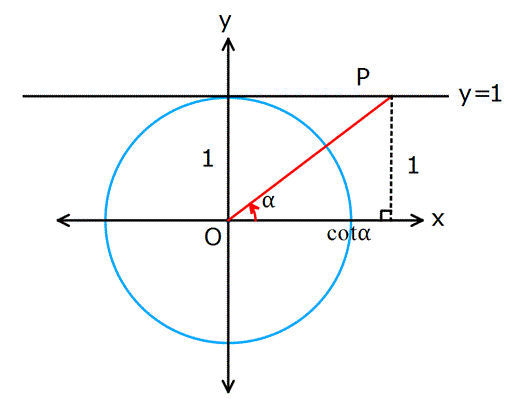
Dik üçgende, komşu dik kenarın karşı dik kenara oranı bize kotanjantı veriyordu(Tanjantın tam tersi).
Birim çemberde ise, açının y=1 doğrusu üzerinde kestiği noktanın apsisidir(Karşı dik kenar 1 birim olduğu için).
Çözüm
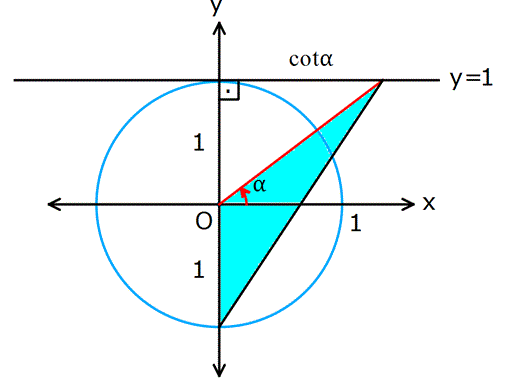

Not: Hem tanjant hem de kotanjant ![]() aralığında her değeri alabilir.
aralığında her değeri alabilir.
Not: tanjant ve kotanjantın bölgelere göre işaretleri aynıdır. 1. ve 3. bölgede pozitif(+) , 2.ve 4. bölgede ise negatif (-) tir. Ayrıca sinüs ve kosinüsten de işaretlerine karar verilebilir. ![]()
Mesela tan300’ün işaretini bulalım. 300 derece 4.bölgededir. sin300=- dir. cos300=+ dır. (-) nin (+) ya bölümü negatif olacağı için tan300=- dir.
Hatırlatma: ![]() dir. (Birbirinin tersi oldukları için)
dir. (Birbirinin tersi oldukları için)
Çözüm

Çözüm


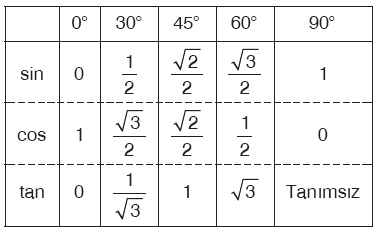
Hatırlatma: Bazı özel açıların trigonometrik oranları, dik üçgen çizilerek bulunabileceği gibi, sıklıkla kullanılacağı için ezbere bilmekte yarar var.
Not: Birim çemberin denklemi ![]() dir. Dolayısıyla
dir. Dolayısıyla ![]() yazabiliriz.
yazabiliriz.
Çözüm

KOSEKANT, SEKANT FONKSİYONU
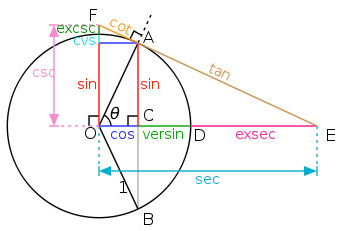
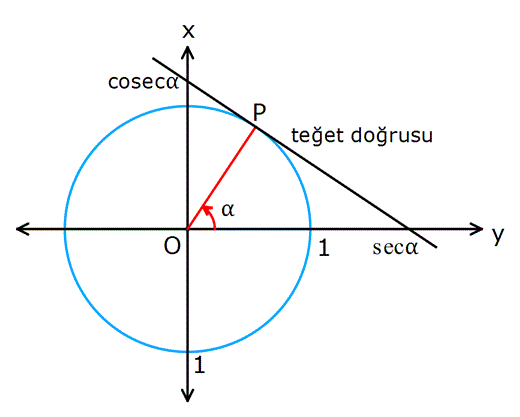
Birim çember üzerindeki açının kestiği noktada teğeti çizilirse, bu doğru x ve y eksenlerini kesecektir. x eksenini kestiği noktaya sekant (sec), y eksenini kestiği noktaya kosekant (cosec) denir.
Not: ![]() ve
ve ![]() dır.
dır.
Not: cosx=0 olduğu durumlarda secx tanımsızdır. sinx=0 olduğu durumlarda da cosecx tanımsızdır.
Not: cosecx ve secx in sonucu (–1, 1) aralığındaki sayılara eşit olamaz.
Örnek: ![]() kaçtır?
kaçtır?
Çözüm
![]() dir.
dir.
![]() tür.
tür.
O halde,
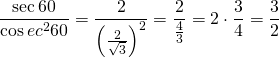 dir
dir
Çözüm
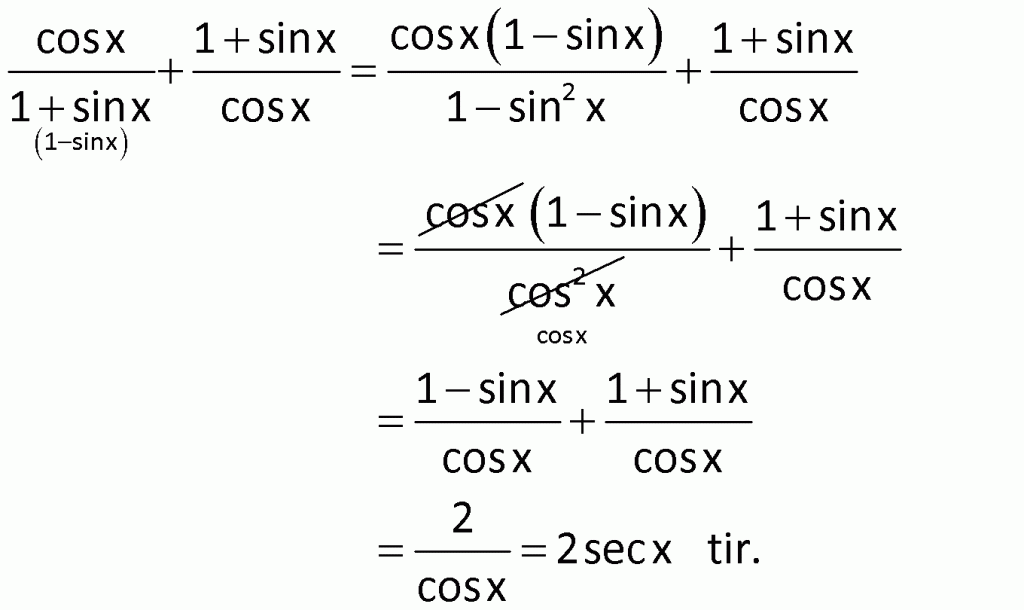
Çözüm