
İşçi problemlerinde oran orantı kullanarak çözüme gidebiliriz.
Örnek:

Çözüm:

Örnek:

Çözüm:

Not:

Örnek:

Çözüm:

Not: İşçi problemlerinde, yapılacak iş miktarını EKOK’la ifade ederek çözüme gidebiliriz.
Örnek:
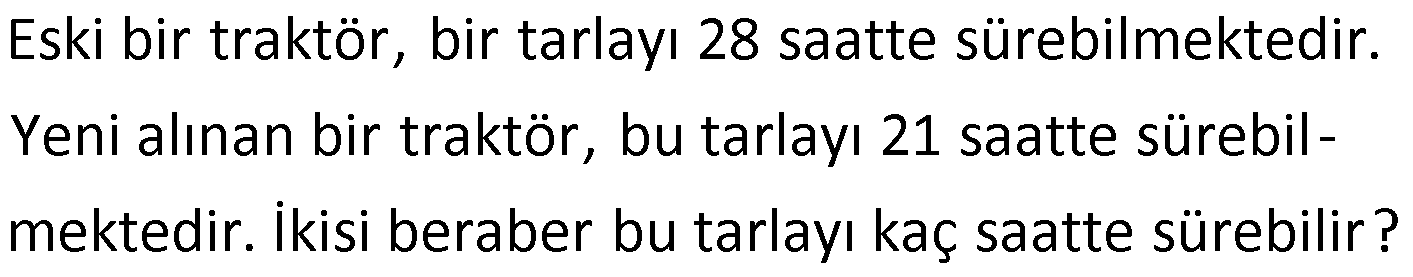
Çözüm:

Örnek:

Çözüm:

Örnek:
Elif bir işi 8 günde yapabiliyor. Ezgi ise bu işi tek başına 6 günde yapabiliyor. İkisi beraber 3 gün çalışırlarsa işin kaçta kaçını yapmış olurlar?
Çözüm:

Not:
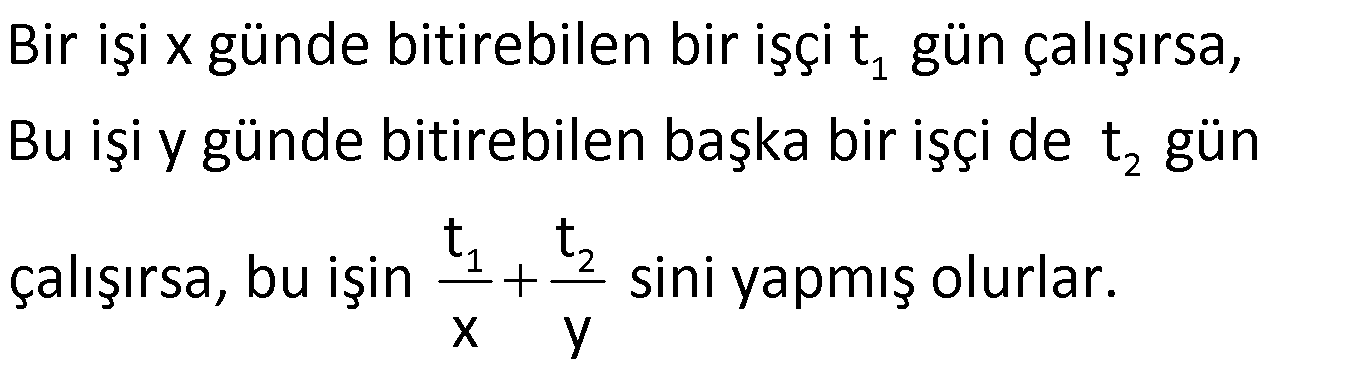
Örnek:

Çözüm:

Örnek:

Çözüm:

Örnek:
12 işçi bir işi 8 günde bitirebiliyor. İşe başladıktan sonra her gün bir işçi işten ayrılıyor. Bu işin kaçta kaçı biter?
Çözüm:

Örnek:
3 usta ve 9 çırak bir işi 3 günde bitirebiliyor. 5 usta ve 12 çırak ise bu işi 2 günde bitiyor. O halde bu işi bir usta tek başına kaç günde bitirebilir?
Çözüm:

Örnek:
Ali’nin iş yapma hızı, Berk’in 3 katı, Can’ın ise yarısı kadardır. Üçü beraber bir işi 9 günde bitirebiliyorsa, Can bu işi tek başına kaç günde bitirebilir?
Çözüm:

Örnek:
Hüseyin bir işi tek başına 17 günde bitirebiliyor. Eğer 1.günden sonra her gün bir önceki güne göre hızını 2 katına çıkarırsa bu işi kaç günde bitirir?
Çözüm:

Örnek:
Aynı boydaki iki mumdan biri 6 saatte, diğeri 8 saatte erimektedir. Aynı anda yakıldıktan kaç saat sonra biri diğerinin 3 katı olur?
Çözüm:

Çözümlü Sorular veya Daha Fazlası için Tıkla
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
İŞÇİ PROBLEMLERİ KONU ANLATIMI www.matematikkolay.net İşçi problemlerinde oran orantı kullanarak çözüme gidebiliriz. Örnek: 2 Zeynep bir işin ‘ini 6 günde yapıyorsa tamamını 5 kaç günde yapar? Çözüm: Tüm iş 5 parça olsun. 2 parça iş 6 günde yapılıyorsa 5 parça iş x günde yapılır. 05.Haz D.O: x 15 günde yapılır. 2 Örnek: Rıza, proje ödevini 12 günde tamamlayabilecektir. Ancak, ödevini yapması için 4 gün kalmıştır. O halde, ödevinin kaçta kaçını bitirebilir? Çözüm: 12 günde 1 ödev yapabiliyorsa, 4 günde x ödev yapar. 4.1 1 D.O: x ‘ünü yapabilir. 12 3 Not: 1 Bir kişi bir işi 6 günde bitirilebiliyorsa, bir günde 6 iş yapabiliyordur. Başka biri bu işi 12 günde bitirilebiliyorsa, bir günde 1 iş yapabiliyordur. 12 1 1 İkisi beraber bir günde, iş yapabilir. 6 12 t gü 1 n beraber çalışıp, bu işi bitirdiklerinde işin ‘i 1 bitmiş olur. Yani 1’e ulaşmış olurlar. Bu durumu, 1 1 t 1 şeklinde ifade edebiliriz. 6 12 2 1 t 1 12 3 t 12 4 1 t 4 günde bu işi bitirirler. Örnek: Hayri, bir işi tek başında 15 günde yapabiliyor. Mehmet ise bu işi tek başına 10 günde yapabiliyor. İkisi beraber bu işi kaç günde bitirebilir? Çözüm: 2 3 1 1 t 1 15 10 2 3 t 1 30 5 t 30 6 1 t 6 günde bitirebilirler. Not: İşçi problemlerinde, yapılacak iş miktarını EKOK’la ifade ederek çözüme gidebiliriz. Örnek: Eski bir traktör, bir tarlayı 28 saatte sürebilmektedir. Yeni alınan bir traktör, bu tarlayı 21 saatte sürebil – mektedir. İkisi beraber bu tarlayı kaç saatte sürebilir? Çözüm: 2 2 Tarlayı, 21 ve 28’in en küçük ortak katı şeklinde ifade edelim. EKOK 21, 28 EKOK 3.7, 2 .7 2 .3.7 84 Tarla 84 parça olsun. 84 Eski traktör 1 saatte 3 parça sürebiliyor. 28 84 Yeni traktör 1 saatte 4 parça 21 3 4 sürebiliyor. İkisi beraber 1 saatte 3 4 7 parça sürebilir. 84 Tüm tarlayı 12 saatte sürebilirler. 7 1 1 3 4 7 t 1 t 1 t 28 21 84 Formül ile çözersek : 84 12 1 t 12 saat buluruz. Örnek: www.matematikkolay.net Mert bir işin yarısını 6 günde, Hakan ise bu işin 1 ünü 8 günde bitirmektedir. İkisi beraber bu işin 3 1 ünü kaç günde bitirebilirler? 4 Çözüm: 2 1 Mert bu işin tamamını 12 günde, Hakan ise 24 günde bitirebilir. 1 İkisi beraber t günde bu işin ‘ünü yapıyorsalar, 4 1 1 1 t 12 24 4 2 1 1 t 24 4 3 t 24 8 1 t 1 4t 8 4 8 4 t 2 günde yaparlar. Örnek: Elif bir işi 8 günde yapabiliyor. Ezgi ise bu işi tek başına 6 günde yapabiliyor. İkisi beraber 3 gün çalışırlarsa işin kaçta kaçını yapmış olurlar? Çözüm: 3 4 1 Elif bir günde iş yapabiliyor. 8 1 Ezgi bir günde iş yapabiliyor. 6 1 1 7 İkisi beraber bir günde iş yapabilir. 8 6 24 3 günde ise 3 7 24 8 3 ‘ini yapmış olurlar. 8 Not: 1 2 1 2 Bir işi x günde bitirebilen bir işçi t gün çalışırsa, Bu işi y günde bitirebilen başka bir işçi de t gün t t çalışırsa, bu işin sini yapmış olurlar. x y Örnek: Furkan 2 gün, Hasan 3 gün çalıştığında bir işin yarısı – nı bitirmiş oluyorlar. Eğer Furkan 4 gün, Hasan 1 gün 4 çalışsaydı bu işin ‘unu bitirmiş olacaklardı. 9 Buna göre, Hasan bu işi tek başına kaç günde bitire – bilir? Çözüm: 2 3 1 İlk bilg iye göre, F H 2 4 1 4 2.bilgiye göre dur. Bu iki denklemi F H 9 çözelim. 2 3 1 2 / F H 2 4 1 4 1 / F H 9 4 6 1 F H 4 1 4 F H 9 5 5 H 9 gün H 9 buluruz. Örnek: Cemile bir işi tek başına 12 günde, Deniz ise bu işi tek başına 16 günde bitirebilmektedir. İkisi beraber 4 gün çalıştık tan sonra Deniz işten ayrılıyor. Kalan işi Cemile kaç günde bitirebilir? Çözüm: İkisi beraber 4 gün Cemile yalnız İşin tamamı 4 3 1 1 t 4 1 şeklinde denklemi 12 16 12 kurabiliriz. 4 3 t 4 1 48 12 4 7 48 12 t 1 12 7 t 1 t 5 günde bitirebilir. 12 Örnek: www.matematikkolay.net 12 işçi bir işi 8 günde bitirebiliyor. İşe başladıktan sonra her gün bir işçi işten ayrılıyor. Bu işin kaçta kaçı biter? Çözüm: Bazen formül kullanmak yerine, daha rahat çözmek için ortak kat kullanabiliriz. Bu işi 12 ile 8’in çarpımı olan 96 parçalık bir işe ben – zetelim. 1 işçi 1 günde 1 parça iş yapabiliyor. İlk gün 12 parça iş yapılır. Bir işçi ayrılır. 2.gün 11 parça 3. gün 10 parça … 12.gün 1 parça iş yapılır ve işçi kalmaz. 12 Toplamda 1 2 … 12 6 .13 2 Son işçi İlk ayrılan işçi 12 gün çal 1 gün çalışmıştır. 78 parça iş yapılır. 78 13 Tüm iş 96 parça idi. ‘sı bitmiş olur. 96 16 Bir işçi bu işi tek başına 96 günde bitirebilir. 1 2 3 12 … 96 96 96 96 Formül ile, ış mıştır. 1 2 … 12 96 12 .13 2 96 8 13 sını yaparlar. 16 Örnek: 3 usta ve 9 çırak bir işi 3 günde bitirebiliyor. 5 usta ve 12 çırak ise bu işi 2 günde bitiyor. O halde bu işi bir usta tek başına kaç günde bitirebilir? Çözüm: 3 2 3 9 3 9 1 İlk bilg i : 3 1 tür. U Ç U Ç 3 5 12 5 12 1 2. bilgi : 2 1 dir. U Ç U Ç 2 Bu iki denklemi çözelim. 3 9 1 4 / U Ç 3 5 12 1 3 / U Ç 2 12 36 4 U Ç 3 15 36 3 U Ç 2 3 3 4 U 2 3 3 9 8 3 1 U 18 U 6 U 6 Bir usta bu işi 18 günde bitirebilir. Örnek: Ali’nin iş yapma hızı, Berk’in 3 katı, Can’ın ise yarısı kadardır. Üçü beraber bir işi 9 günde bitirebiliyorsa, Can bu işi tek başına kaç günde bitirebilir? Çözüm: Berk’in 1 günde yaptığı iş miktarına 1 parça diyelim. Ali 3 parça iş yapar. Can 6 parça iş yapar. Üçü beraber bir günde 10 parça iş yapar. 9 günde 90 parça iş yapmış olurlar. 90 parçalık bu işi Can t ek başına, 90 15 günde yapabilir. 6 Örnek: Hüseyin bir işi tek başına 17 günde bitirebiliyor. Eğer 1.günden sonra her gün bir önceki güne göre hızını 2 katına çıkarırsa bu işi kaç günde bitirir? Çözüm: www.matematikkolay.net 1.gün 2.gün 3.gün 4.gün Normalde bir günde yaptığı iş miktarına a diyelim. 17 günde 17a parça iş yapar. Hızını artırarak devam ederse, a 2a 4a 8a … şeklinde ilerler. İlk 4 günün toplamı 17a dır. O halde 4 günde bu iş biter. Örnek: Aynı boydaki iki mumdan biri 6 saatte, diğeri 8 saatte erimektedir. Aynı anda yakıldıktan kaç saat sonra biri diğerinin 3 katı olur? Çözüm: 1 Mumlardan biri her saat ‘sını kaybediyor, diğeri 6 1 ise ‘ini kaybediyor. t saat sonra biri diğerinin 3 8 katı oluyorsa, t t 1 3 1 şeklinde bir eşitlik kurabiliriz. 8 6 t t 1 3 8 2 t t 2 2 8 6 3 t 8 4 8 2 3t 8 t saat sonra gerçekleşir. 3

