FAKTÖRİYEL
1 den n ye kadar olan sayma sayılarının çarpımına n faktöriyel denir ve n! biçiminde gösterilir.
Örnek:
3!+4!=?
Çözüm
3!=3.2.1=6 dır.
4!=4.3.2.1=24 tür. Toplarsak,
6+24=30 buluruz.
Örnek:
Çözüm
buluruz.
Alıştırma 7
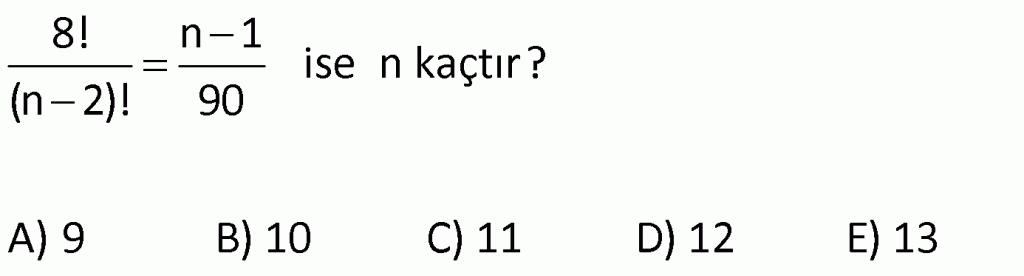
| | | | | |
Çözüm

Alıştırma 8
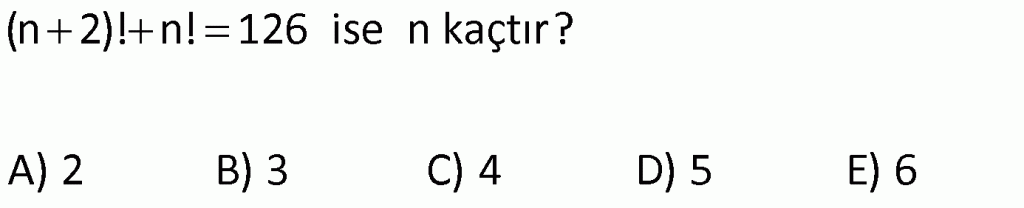
| | | | | |
Çözüm

PERMÜSTASYON
r ve n doğal sayı ve r ≤ n olmak üzere, n elemanlı bir kümenin r elemanlı sıralı r lilerine bu kümenin r li permütasyonları denir.
n elemanlı kümenin r li permütasyonlarının sayısı :
Kısaca, n’den itibaren 1’er tane azaltarak r tane sayıyı çarpma işlemidir.
Örnek:
P(7,3)=7.6.5=210
P(4,2)=4.3=12 dir. Ayrıca,
P(n, n) = n!
P(n, 1) = n
P(0, 0)=0! = 1
P(n, 0)=1
P(n, n-1)=n! dir.
Örnek:
P(5, 2) – P(4, 1) = ?
Çözüm
5.4 – 4 = 20 – 4 = 16 dır.
Alıştırma 9
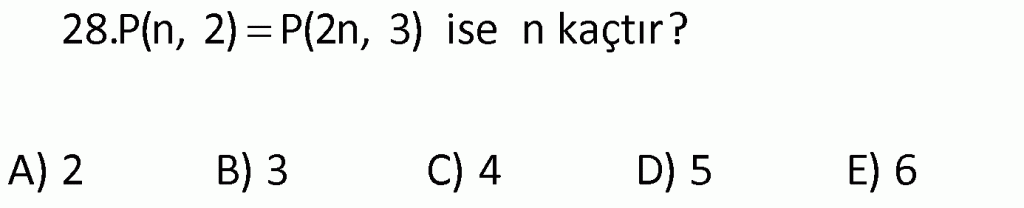
| | | | | |
Çözüm
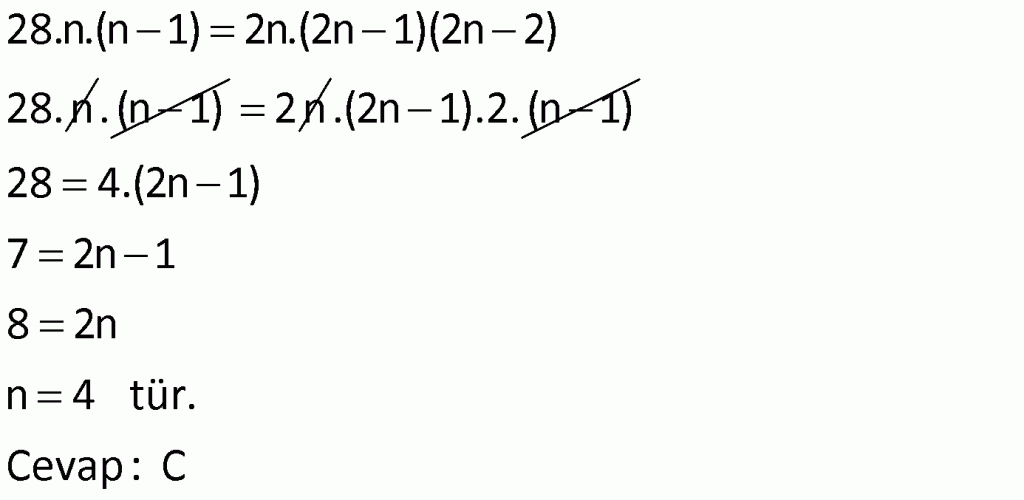
Örnek:
A={1,2,3,4,5} kümesinin 3 lü permütasyonlarının sayısını bulunuz.
Çözüm
A kümesi 5 elemanlı bir kümedir. Bu 5 elemandan 3’ünü seçip sıralayacağız. Bu sebeple P(5 ,3) ü hesaplamalıyız.
P(5, 3) = 5.4.3 = 60 buluruz.
Alıştırma 10

 | | | | |
Çözüm

Örnek:
4 kız ve 3 erkek, kızlar yan yana olacak şekilde kaç farklı şekilde sıralanabilirler?
Çözüm
İlk önce kızları tek bir kişiymiş gibi düşünelim. 3 de erkek olduğu için toplamda 4 kişilermiş gibi düşüneceğiz. 4 kişi 4! şeklinde sıralanabilir.
Ayrıca kızlar kendi arasında 4! şeklide yer değiştirebilir. Dolayısıyla,
4!.4!=24.24=576 farklı şekilde sıralanabilirler.
Alıştırma 11

| | | | | |
Çözüm


