Parabol

İkinci Dereceden Bir Değişkenli Fonksiyonlar

Şeklinde ikinci dereceden bir değişkenli fonksiyonların grafiklerine parabol adı verilir.

Örnek:

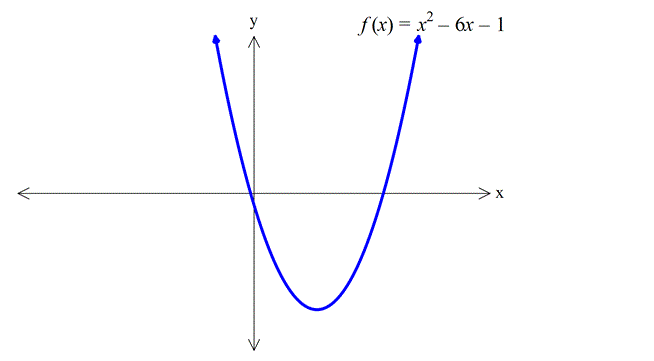
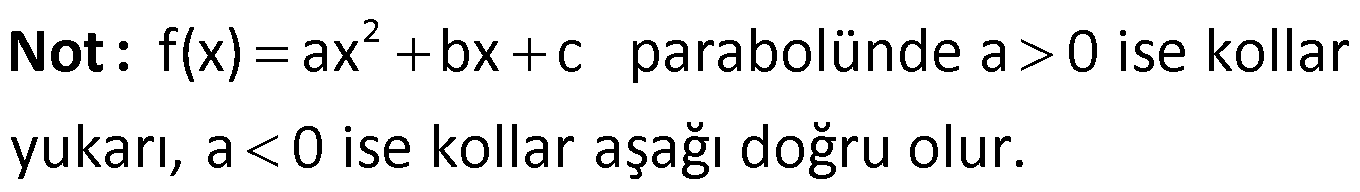
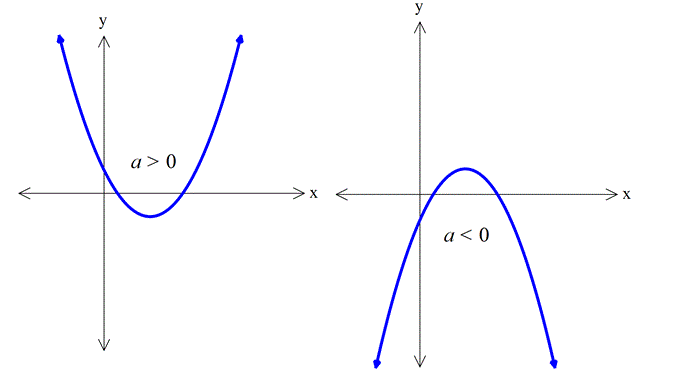
Örnek:

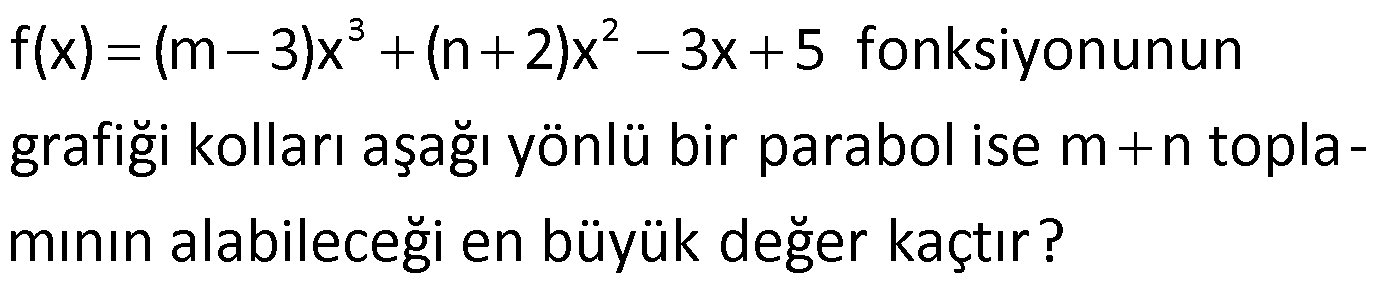
Çözüm:

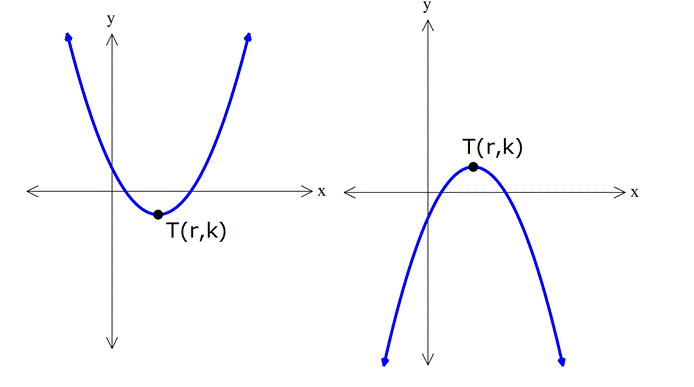
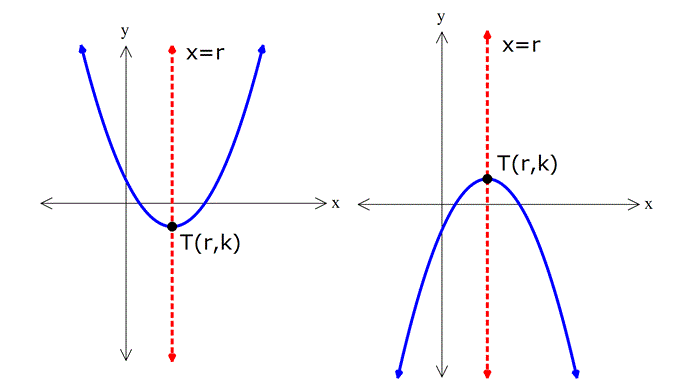
Tepe Noktası

Parabolün kollarının durumuna göre en yüksek ya da en alçak noktasıdır.

Örnek:

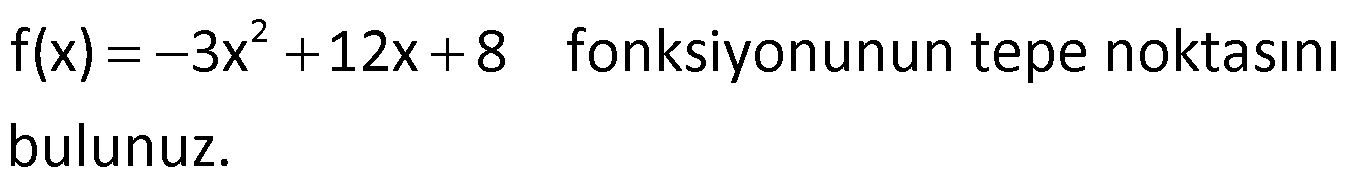
Çözüm:

Örnek:

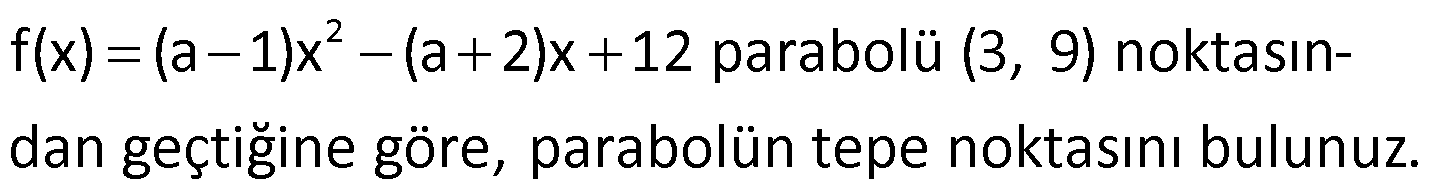
Çözüm:

Not: Parabolün simetri ekseni x=r dir. Yani

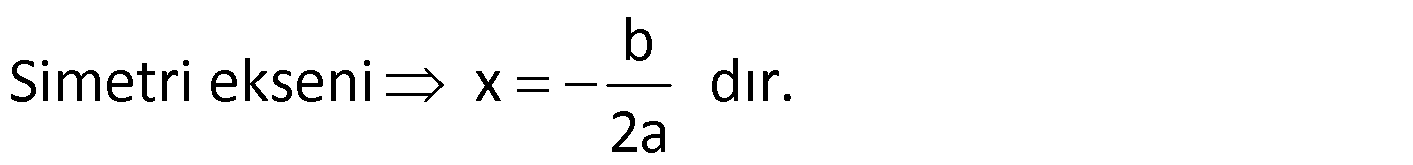
Örnek:

Örnek:

Çözüm:

Not:

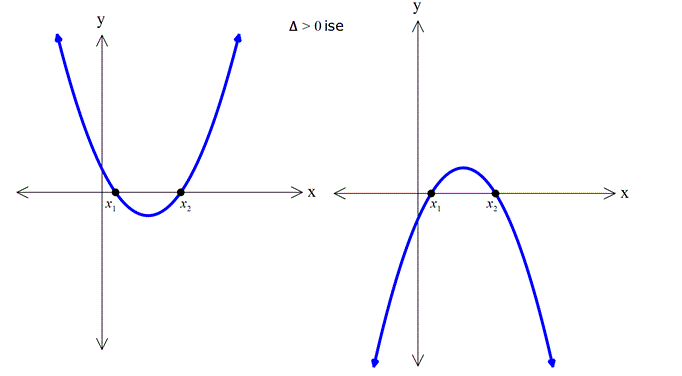
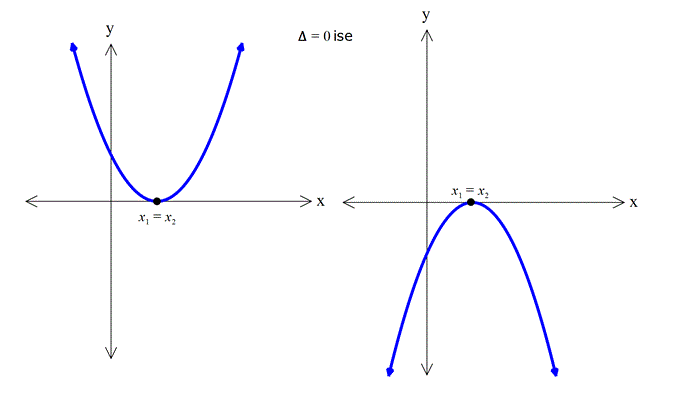
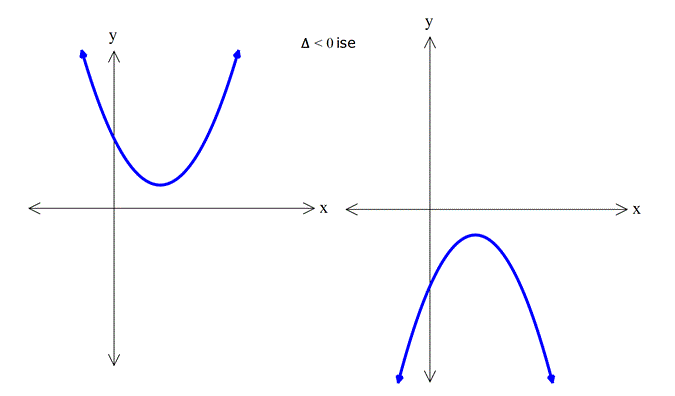
Örnek:

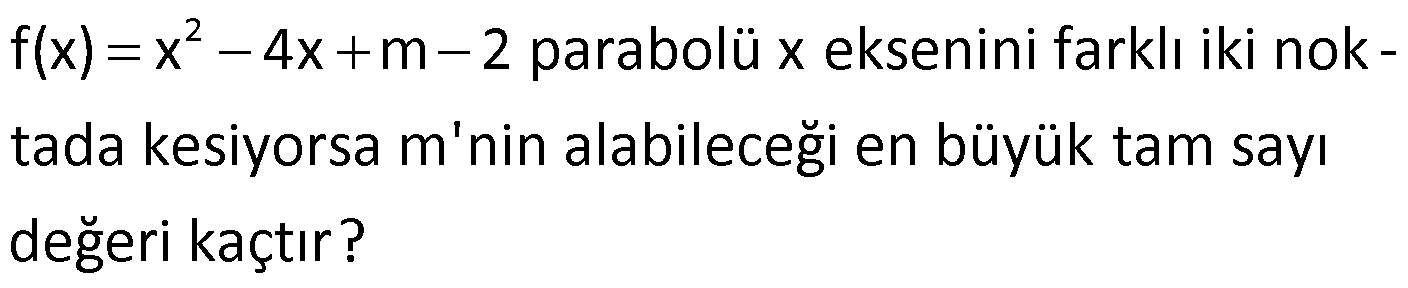
Çözüm:

Örnek:

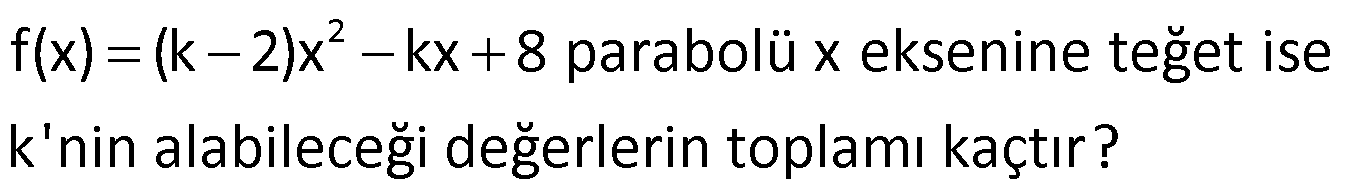
Çözüm:

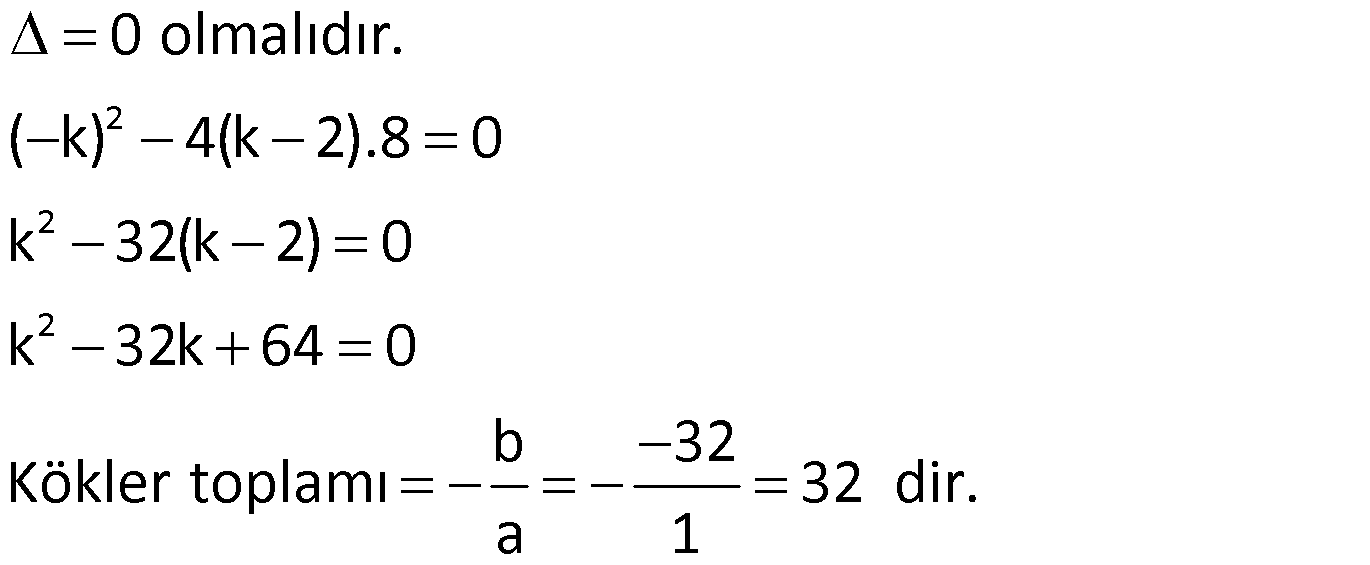
Örnek:

Çözüm:

Parabolün Çizimi

Parabol çizerken, a’nın işareti çok önemlidir.  Daha sonra parabolün eksenleri kestiği noktalar ve tepe noktası gibi önemli noktalar bulunmaya çalışılır. Bulunan noktalar kullanılarak kabaca çizim yapılır.

Örnek:

Çözüm:

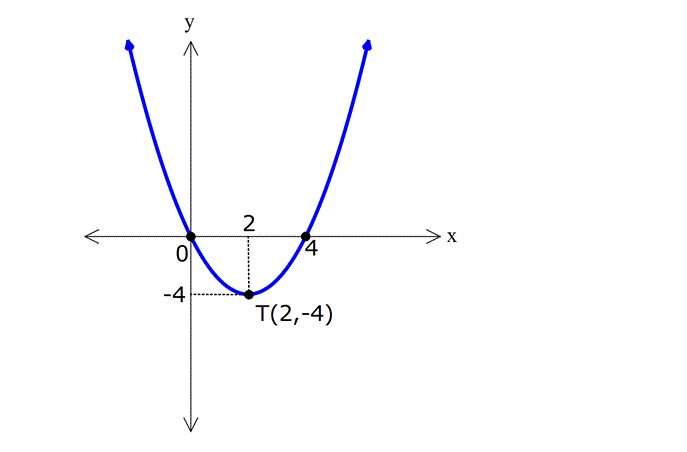
Örnek:

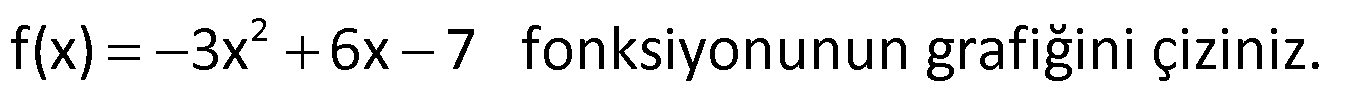
Çözüm:

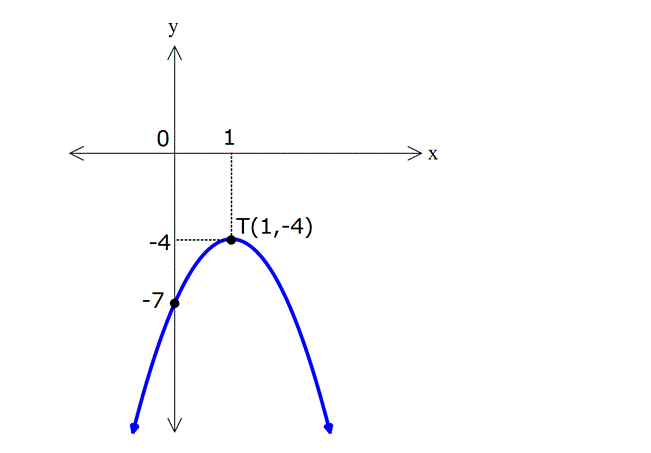
Not:

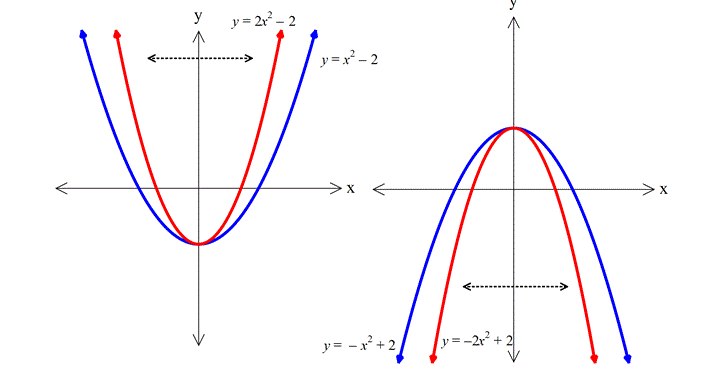
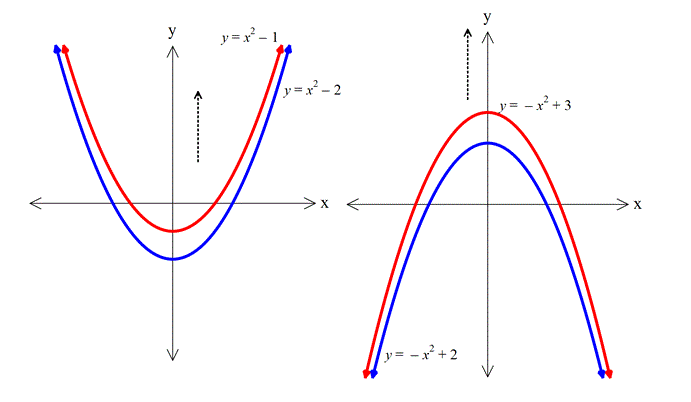
Not:

Parabol Grafiğinden Fonksiyonu Yazma

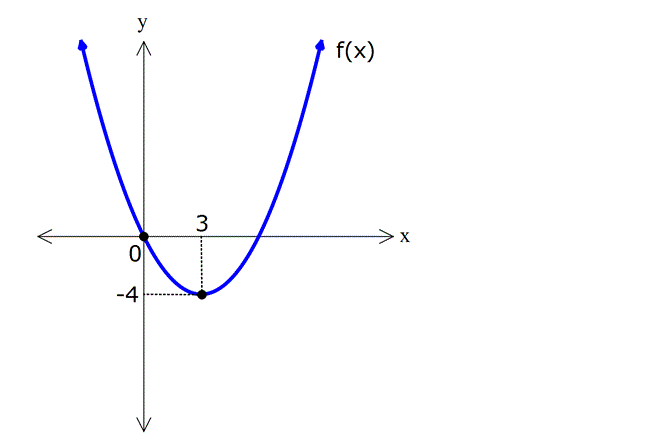
1.Tepe Noktası Biliniyorsa

Örnek:

2.Parabolün Üç Noktası Biliniyorsa

Örnek:

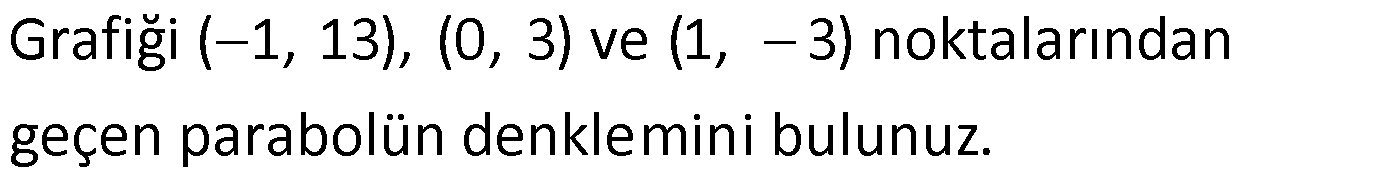
Çözüm:

Not:

Örnek:

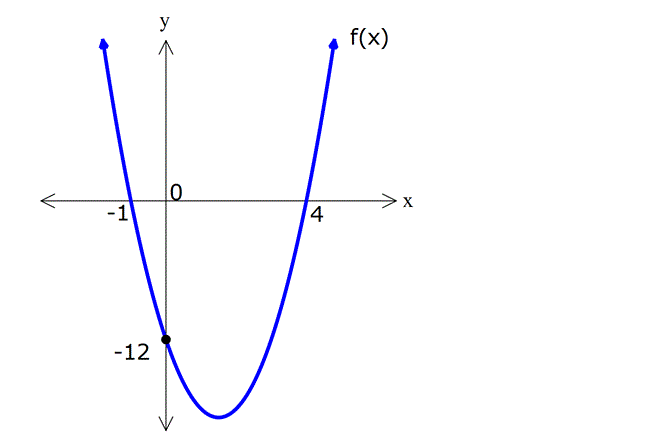
Örnek:

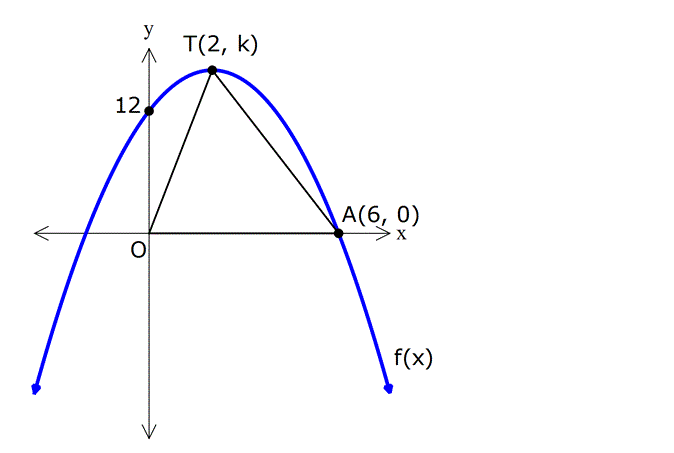
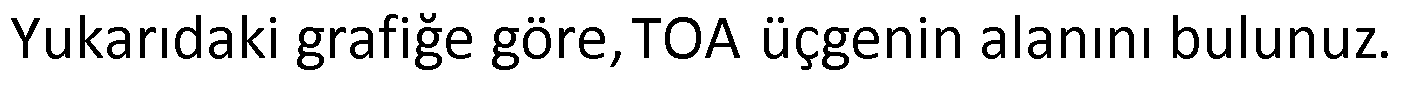
Çözüm:

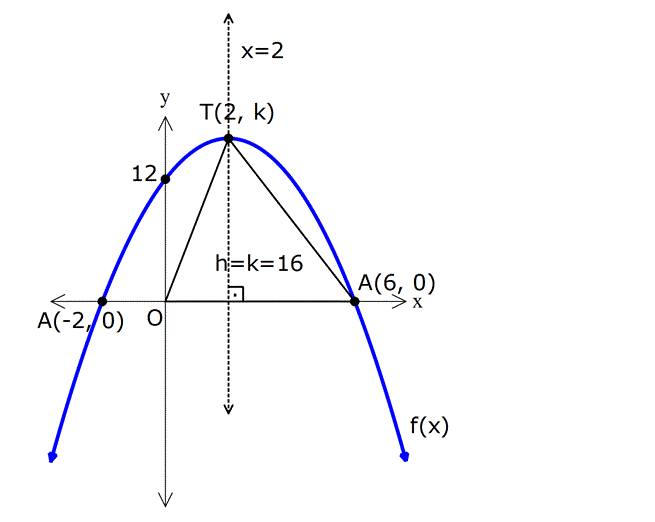
Bir Doğru ile Bir Parabolün Birbirine Göre Durumu

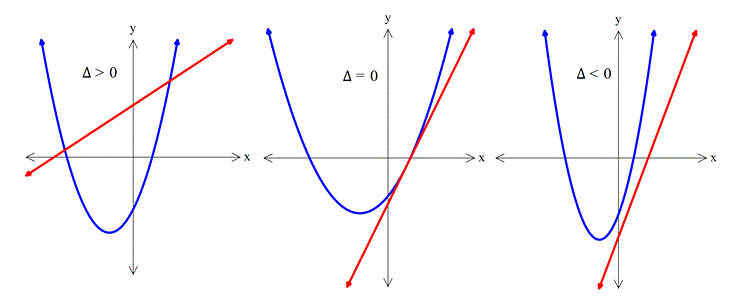
Ortak çözümden gelen x değerleri kesişim noktalarının apsisleridir. Daha sonra bu x değerleri herhangi bir denklemde yerine yazılarak y değerleri bulunabilir.

Örnek:

Çözüm:

Örnek:

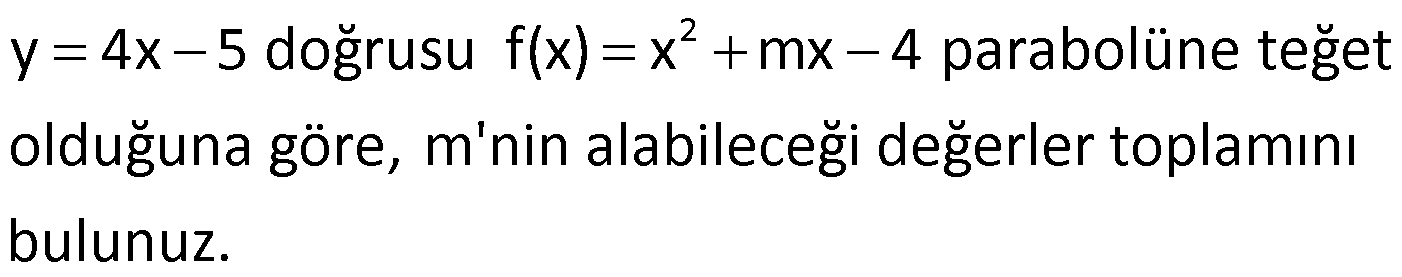
Çözüm:

Örnek:

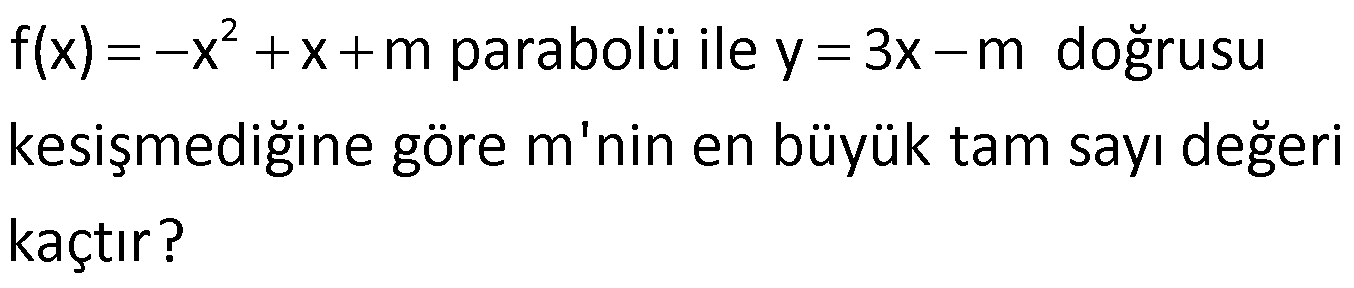
Çözüm:

Örnek:

Çözüm:

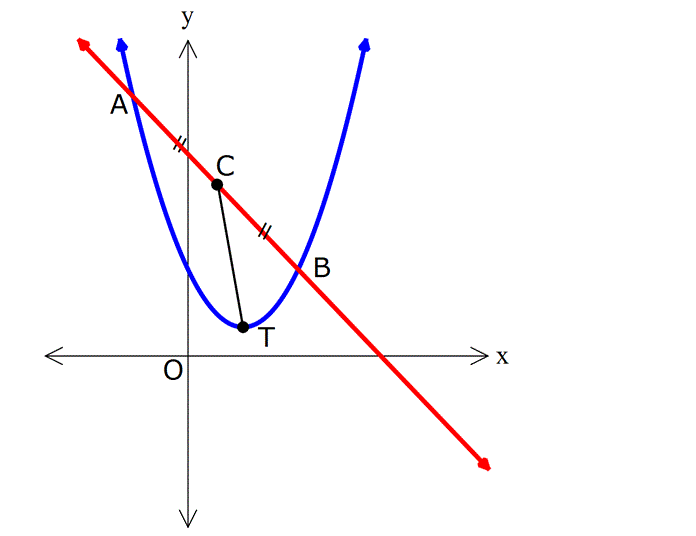
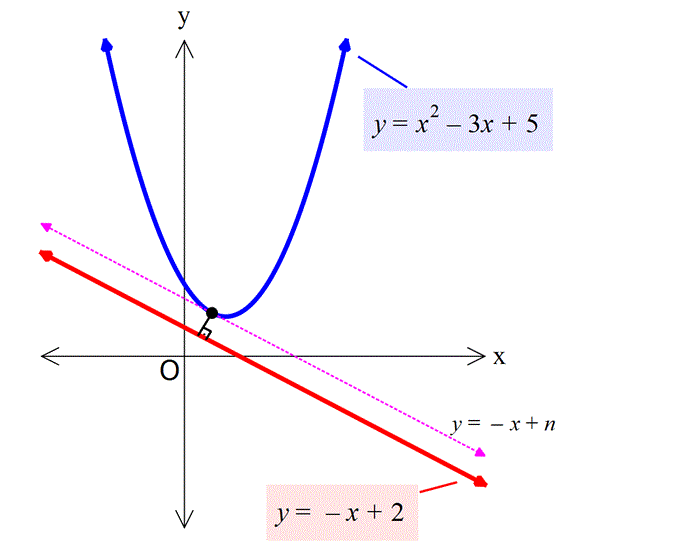
Örnek:

Çözüm:

Problem Çözümünde Parabolün Kullanılması

Örnek:

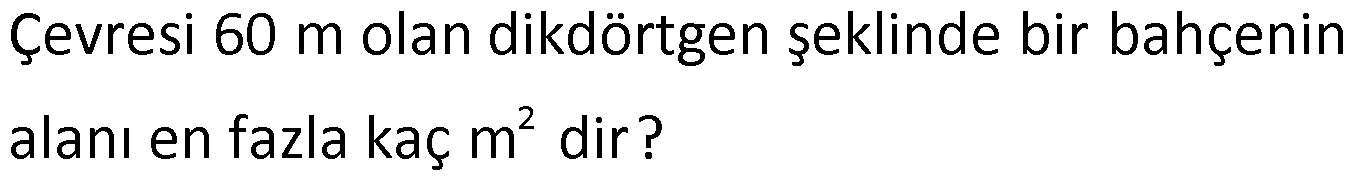
Çözüm:     

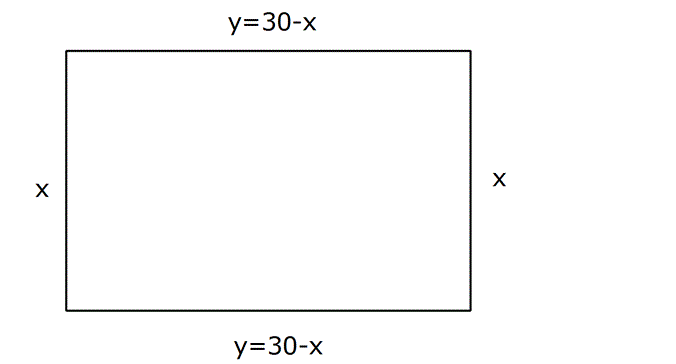
Örnek:

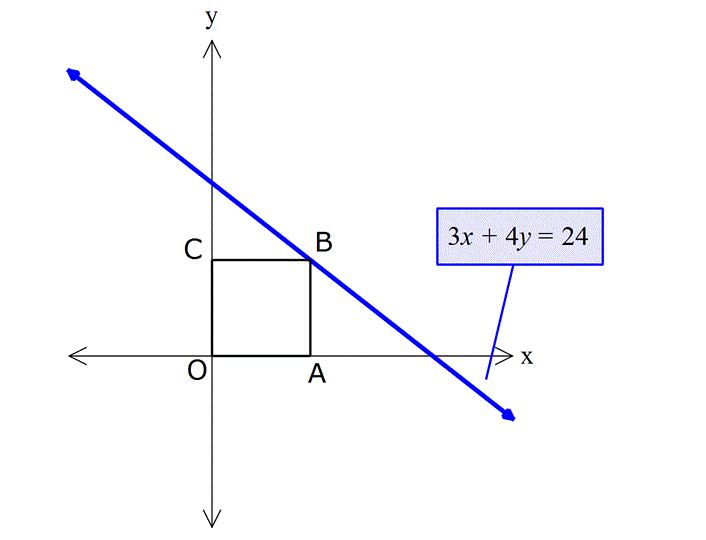
Çözüm:   

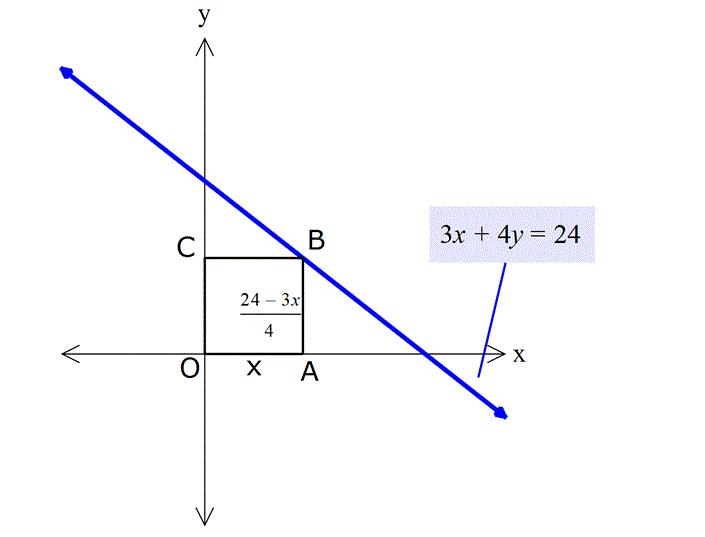
Örnek:

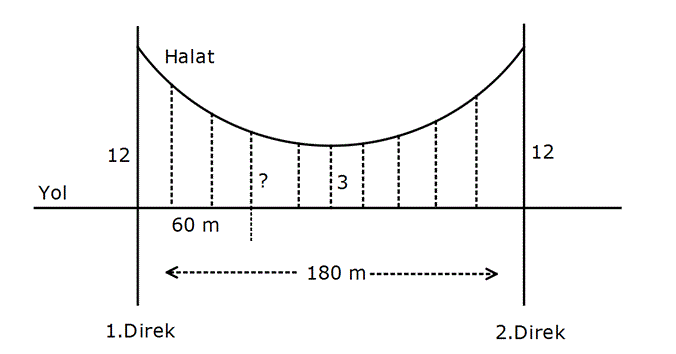
Çözüm: