Konu ile ilgili Çözümlü Soruları Görmek için Tıkla
a, b, m birer tam sayı ve m ≥ 1 olmak üzere, tam sayılar kümesi üzerinde tanımlanan,
β = {(a, b) : m, (a – b) yi tam böler} bir denklik bağıntısıdır.
β denklik bağıntısı olduğundan Her (a, b) ∈ β için,
a ≡ b (mod m)
biçiminde yazılır ve m modülüne göre a sayısı b ye denktir denir.
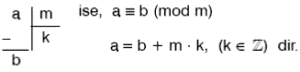
Tam sayıların m sayma sayısı ile bölünmesiyle elde edilen kalanlar, 0, 1, 2, 3, 4, … , (m – 1) dir.
Her tam sayı m ile bölündüğünde hangi kalanı veriyorsa o kalana denktir. Bu kalanların her biri, belirlediği denklik sınıfının temsilci elemanı olarak alınırsa, denklik sınıfları
![]()
Bu denklik sınıflarının kümesine m nin kalan sınıflarının kümesi denir ve Z/m biçiminde gösterilir.
Buna göre,
![]()
n bir sayma sayısı ve k bir tam sayı ve a ≡ b (mod m)
c ≡ d (mod m) olmak üzere,
1. a + c ≡ b + d (mod m)
2. a – c ≡ b – d (mod m)
3. a . c ≡ b . d (mod m)
4. a ≡ b
(mod m)
5. a – b ≡ 0 (mod m)
6. k . a ≡ k . b (mod m) dir.
7. n sayma sayısı; a, b, m sayılarının ortak böleni ise dir.
8. a ile m ve b ile m aralarında asal olmak üzere, dir.
Z/m deki işlemler (mod m) ye göre yapılır.
• x, m nin tam katı olmayan pozitif bir tam sayı ve m bir asal sayı ise, 1 (mod m) dir.
x in (m – 1) den daha küçük kuvvetinde de 1 bulunabilir.
• x ile m aralarında asal sayılar olmak üzere, m nin asal çarpanlarının kuvvetleri biçiminde yazılmış hâli olmak üzere,
ise,
(mod m)
m asal sayı ise, (m – 1)! + 1≡ 0 (mod m) dir.
Kaynak: www.derscalisiyorum.com
Konu ile ilgili Çözümlü Soruları Görmek için Tıkla

