Logaritma Konu Anlatımı

4.sayfaya dönmek için tıklayınız.

Üstel Eşitsizlikler

$\displaystyle {{a}^{{f(x)}}}>{{a}^{{g(x)}}}$ eşitsizliğinde

$\displaystyle a>1$ ise $\displaystyle f(x)>g(x)$ tir.

$\displaystyle 0<a<1$ ise $\displaystyle f(x)<g(x)$ tir.

Alıştırma-20

Çözüm için Tıklayınız.

Logaritmalı Eşitsizlikler

$\displaystyle a>1$ için $\displaystyle 0<{{x}_{1}}<{{x}_{2}}\Leftrightarrow {{\log }_{a}}{{x}_{1}}<{{\log }_{a}}{{x}_{2}}$ dir.

$\displaystyle 0<a<1$ için $\displaystyle 0<{{x}_{1}}<{{x}_{2}}\Leftrightarrow {{\log }_{a}}{{x}_{1}}>{{\log }_{a}}{{x}_{2}}$ dir.

Örnek 24:

$\displaystyle {{\log }_{4}}(3x-7)>{{\log }_{4}}(5-x)$ eşitsizliğinin çözüm kümesini bulunuz.

Çözüm için Tıklayınız.

Logaritmanın tabanı 1 den büyük olduğu için, eşitsizliğin yönünü değiştirmeye gerek yok.

$\displaystyle 3x-7>5-x$

$\displaystyle 4x>12$

$\displaystyle x>3$ tür. Ayrıca tanım gereği logaritmanın içi pozitif olmalıdır. Yani $\displaystyle 3x-7>0$ ve $\displaystyle 5-x>0$ olmalıdır.

$\displaystyle 3x-7>0\text{ }\Rightarrow \text{ }x>\frac{7}{3}$

$\displaystyle 5-x>0\text{ }\Rightarrow \text{ }x<5$

O halde, Ç.K.= $\displaystyle (3,\text{ 5})$ aralığıdır.

Örnek 25:

$\displaystyle {{\log }_{{\frac{1}{2}}}}(3x+2)<1$ eşitsizliğinin çözüm kümesini bulunuz.

Çözüm için Tıklayınız.

Logaritmanın tabanı 1 den küçük olduğu için, eşitsizliğin yönü değişir.

$\displaystyle 3x+2>\frac{1}{2}$

$\displaystyle 3x>-\frac{3}{2}$

$\displaystyle x>-\frac{1}{2}$ dir.

Bu aralıkta logaritmanın içi negatif olmadığı için bunu direkt çözüm kümesi olarak yazabiliriz.

Ç.K.= $\displaystyle \left( {-\frac{1}{2},\text{ }\infty } \right)$ aralığıdır.

Alıştırma-21

Çözüm için Tıklayınız.

Alıştırma-22

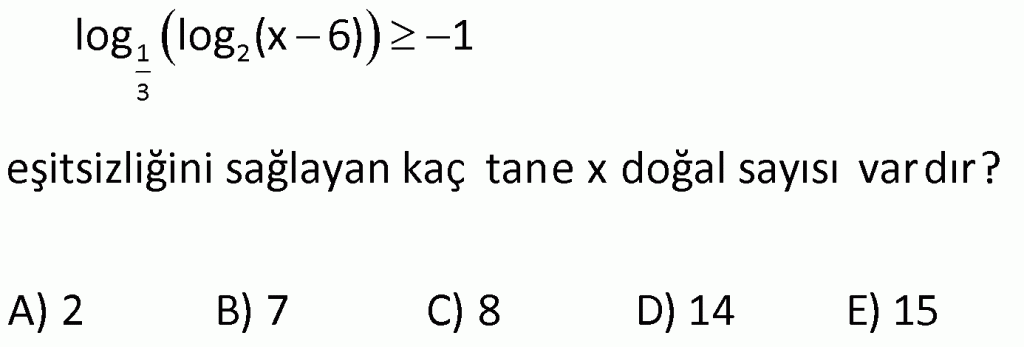
Çözüm için Tıklayınız.

Örnek 26:

$\displaystyle {{\log }_{2}}19$ sayısı hangi iki tam sayı arasındadır?

Çözüm için Tıklayınız.

2 nin kuvvetlerinden 19’un etrafında olan sayılar nelerdir? 16 ve 32.

$\displaystyle {{\log }_{2}}16=4$ ve $\displaystyle {{\log }_{2}}32=5$ olduğuna göre, $\displaystyle {{\log }_{2}}19$ sayısı 4 ile 5 arasında olacaktır.

Alıştırma-23

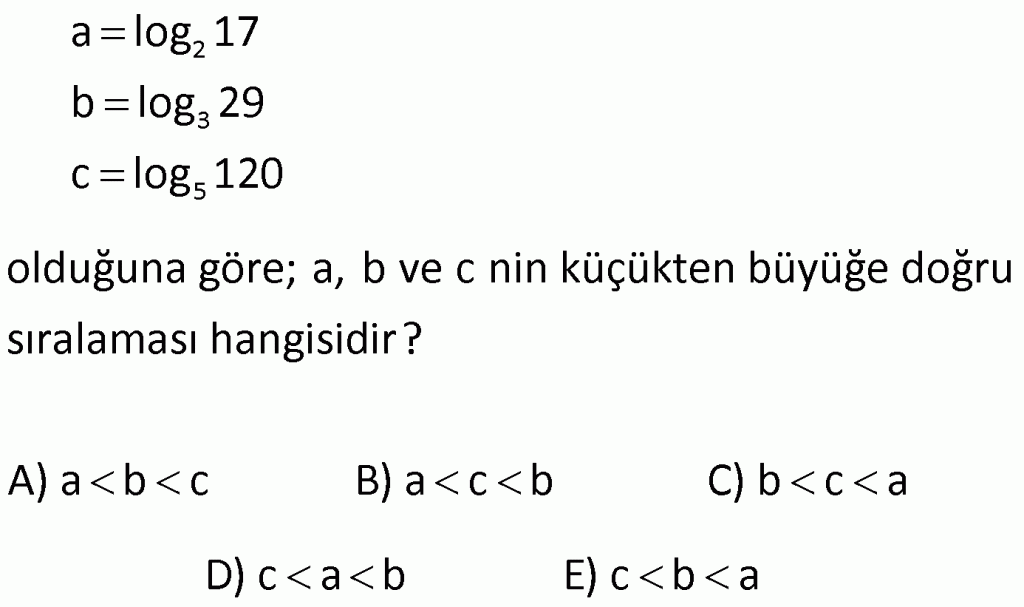
Çözüm için Tıklayınız.

Basamak Sayısı ile ilgili örnekler

$\displaystyle 1000\text{ }\Rightarrow \text{ }3\text{ }basamakl\imath \text{ },\text{ }\log 1000=\log {{10}^{3}}=3$ tür.

$\displaystyle 10000\text{ }\Rightarrow \text{ 4 }basamakl\imath \text{ },\text{ }\log 10000=\log {{10}^{4}}=4$ tür.

$\displaystyle 5000\text{ }\Rightarrow \text{ 4 }basamakl\imath \text{ },\text{ }\log 5000\cong 3,69897$

Not: 10 tabanında logaritmanın sonucu virgüllü pozitif bir ifade ise, ondalık sayının tam kısmından 1 fazlası kadar basamak vardır.

Örnek 27:

$\displaystyle \log 2\cong 0,301$ olduğuna göre, $\displaystyle {{2}^{{20}}}$ kaç basamaklı bir sayıdır?

Çözüm için Tıklayınız.

$\displaystyle \log {{2}^{{20}}}=20\log 2=20.(0,301)=6,02\text{ }dir.$

Dolayısıyla 6+1=7 basamaklıdır.

( $\displaystyle {{2}^{{20}}}=1048576\text{ }\Rightarrow \text{ 7 basamakl }\!\!\imath\!\!\text{ }$ )

$\displaystyle 0,001\text{ }\Rightarrow$ $\displaystyle \log 0,001=\log {{10}^{{-3}}}=-3$ tür.

$\displaystyle 0,0001\text{ }\Rightarrow$ $\displaystyle \log 0,0001=\log {{10}^{{-4}}}=-4$ tür.

$\displaystyle 0,0005\text{ }\Rightarrow$ $\displaystyle \log 0,0005\cong -3,3010$ dur.

Örnek 28:

$\displaystyle \log (0,085)$ in tam kısmındaki sayı kaçtır?

Çözüm için Tıklayınız.

$\displaystyle 0,01<0,085<0,1$

$\displaystyle \log 0,01<\log 0,085<\log 0,1$

$\displaystyle -2<\log 0,085<-1\text{ }\Rightarrow \text{ }\log 0,085\cong -1,...$ şeklindedir.

Cevap: -1

Alıştırma-24

Çözüm için Tıklayınız.

Konu Bitti. Logaritma Üst Başlık için Tıklayınız.

Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)

Sayfalar: 1 2 3 4 5