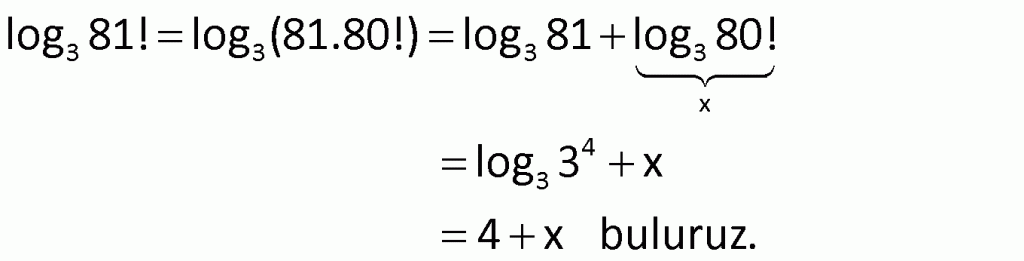Onluk Logaritma Fonksiyonu
Tabanı 10 olan logaritma fonksiyonuna onluk logaritma fonksiyonu (bayağı logaritma) denir.
şeklinde yazılır.
Örnek 6:
Örnek 7:
Cevabı Gör
tür.
Doğal Logaritma
e 2,71828182845… olup bu sayı irrasyoneldir. Matematik, kimya, iktisat, istatistik gibi alanlarda kullanılmaktadır.
Tabanı e olan logaritma fonksiyona doğal logaritma fonksiyonu denir.
şeklinde yazılır.
Örnek 8:
dır.
LOGARİTMA FONKSİYONUNUN ÖZELLİKLERİ
Her tabana göre, 1 in logaritması 0 dır. Buna göre,
Örnek 9:
Cevabı Gör
dir.
Alıştırma-5
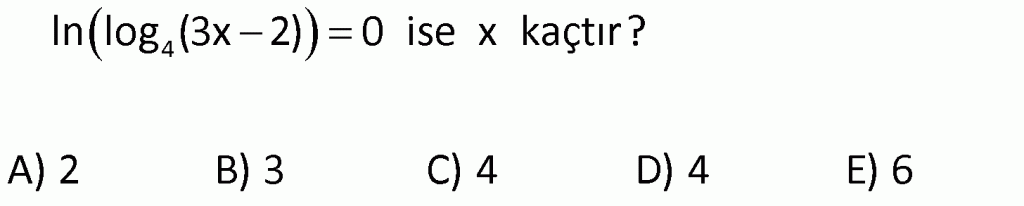
 | | | | |
Çözüm için Tıklayınız.

Logaritmada üslerin başa çarpan olarak gelmesi
Örnek 10:
dir.
tür.
dir.
Örnek 11:
Cevabı Gör
buluruz.
Alıştırma-6
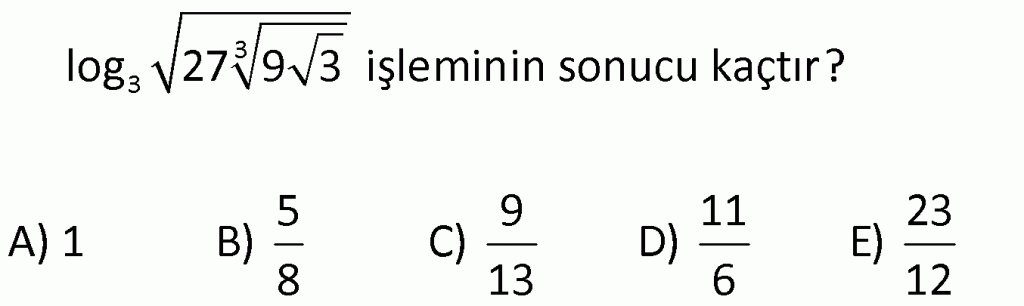
| | | | | |
Çözüm için Tıklayınız.

Logaritma içinde Çarpma Bölme
dir.
Örnek 12:
dir.
dir.
dir.
tir.
Örnek 13:
Çözüm için Tıklayınız.
dir.
Örnek 14:
Çözüm için Tıklayınız.
tür.
Örnek 15
ise
nin x cinsinden eşitini bulunuz.
Çözüm için Tıklayınız.
dir.
Örnek 16
ise
ifadesinin x ve y cinsinden eşitini bulunuz.
Çözüm için Tıklayınız.
dir. O halde,
dir.
Örnek 17:
ise
i x cinsinden eşitini nedir?
Çözüm için Tıklayınız.
tir.
Örnek 18:
olduğuna göre,
yi a ve b cinsinden ifade ediniz.
Çözüm için Tıklayınız.
dır.
Alıştırma-7
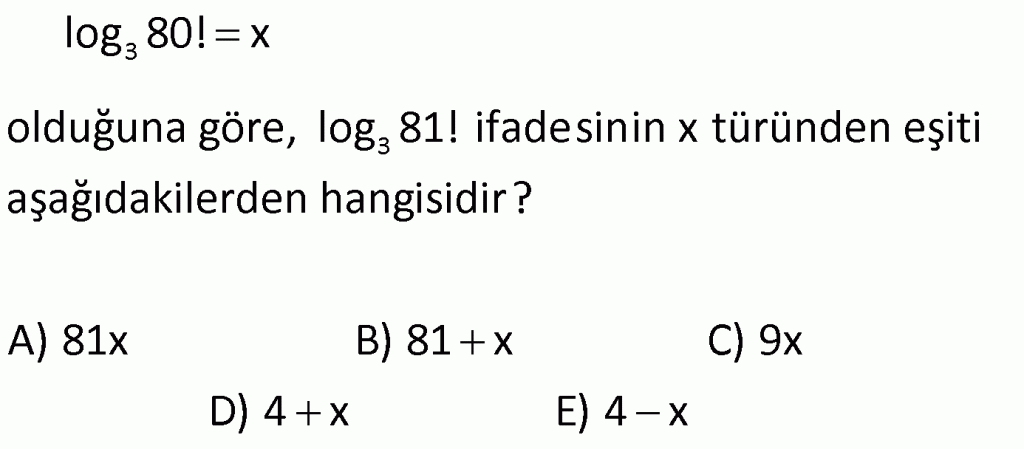
| | | | | |
Çözüm için Tıklayınız.