 Konu ile ilgili Çözümlü Sorular veya Çıkmış Sorular için Tıkla
Konu ile ilgili Çözümlü Sorular veya Çıkmış Sorular için Tıkla
r, n ∈ N ve r≤n olmak koşuluyla, n elemanlı bir A kümesinin r elemanlı alt kümelerinin her birine, A kümesinin r li kombinasyonu denir.
n elemanlı kümenin r li kombinasyonlarının sayısı, C(n, r) ya da ![]() ile gösterilir.
ile gösterilir.
![]() dir.
dir.
Not: Permütasyonda sıralama önemli iken, Kombinasyonda sıralama önemli değildir. Örneğin, a-b ve b-a şeklinde sıralama permütasyonda iki farklı durum iken; {a, b} ve {b, a} kümeleri kombinasyon için aynı durumdur. Çünkü ikisi de aynı kümedir.
Bu sebeple, ![]() dir.
dir.
Örnek: ![]()
Çözüm için Tıklayınız.
![]() dir.
dir.
Örnek: ![]()
Çözüm için Tıklayınız.
![]() dur.
dur.
Alıştırma 1
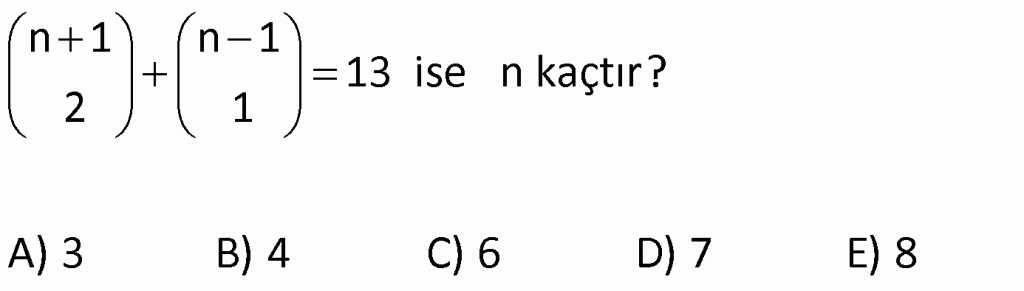
| | | | | |
Çözüm
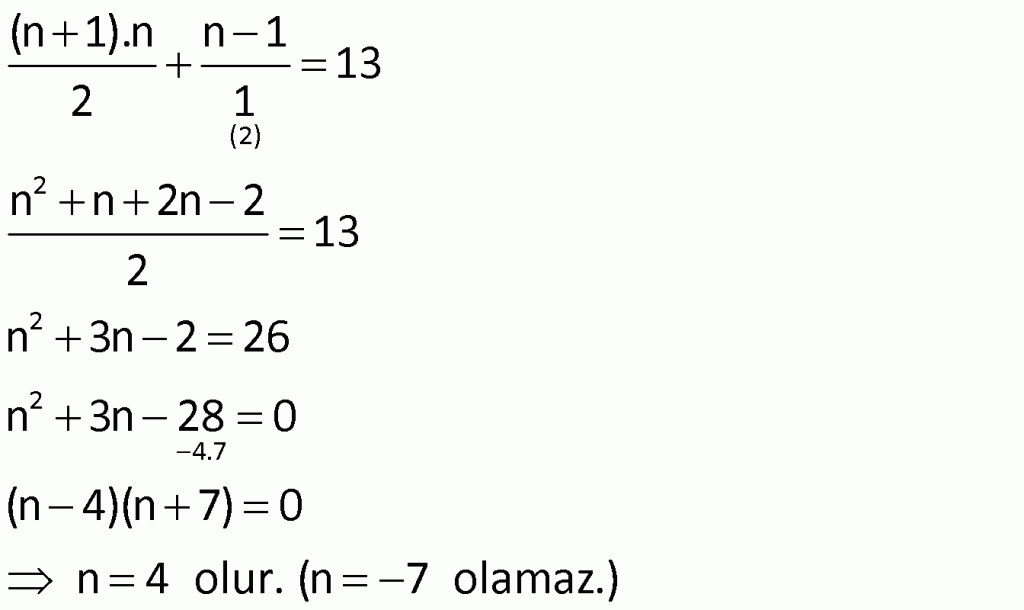
Kural: ![]() dir.
dir.
Mesela, ![]() ile
ile ![]() birbirine eşittir.
birbirine eşittir.
Bu sebeple ![]() eşitliğini gördüğümüzde iki ihtimal düşüneceğiz: a=b olabilir ya da a+b=n olabilir.
eşitliğini gördüğümüzde iki ihtimal düşüneceğiz: a=b olabilir ya da a+b=n olabilir.
Örnek: ![]() ise a’nın alabileceği değerler çarpımı kaçtır?
ise a’nın alabileceği değerler çarpımı kaçtır?
Çözüm
![]() ya da
ya da ![]() olabilir. Bu değerleri çarparsak
olabilir. Bu değerleri çarparsak ![]() buluruz.
buluruz.
Alıştırma 2
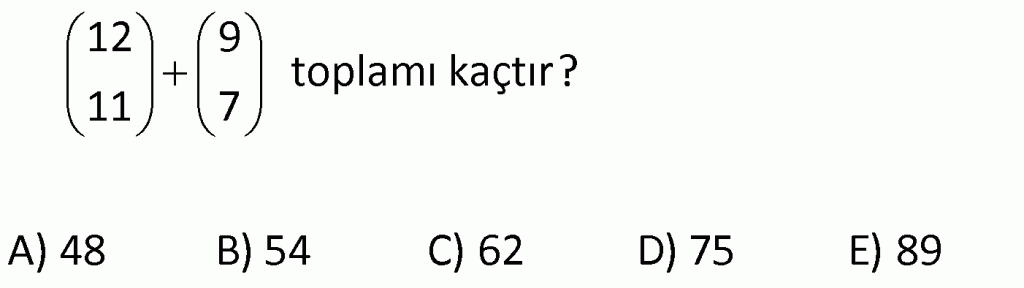
 | | | | |
Çözüm

Kural: ![]() dir.
dir.
Bunu kümeler gibi düşünebiliriz.
n elemanlı bir kümenin alt küme sayısı ![]() dir.
dir.
Boş küme alt kümesidir. ![]()
1 elemanlı alt küme sayısı ![]() dir.
dir.
2 elemanlı alt küme sayısı ![]() dir.
dir.
…
Kendisi de bir alt kümedir. ![]() dir.
dir.
Dolayısıyla bu alt kümelerin toplamı ![]() i vermek zorundadır.
i vermek zorundadır.
Örnek: ![]()
Çözüm
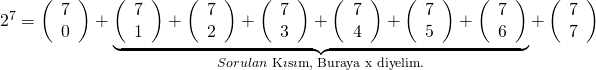
![]()
![]()
![]() buluruz.
buluruz.
Not: ![]() dir.
dir.
Kural: ![]() dir.
dir.
Örnek: ![]() eşit midir? İnceleyelim.
eşit midir? İnceleyelim.
![]() dır.
dır.
![]() tür.
tür.
Toplamları 6+4=10 yapar.
![]() dur, eşitliği sağlar.
dur, eşitliği sağlar.
Alıştırma 3
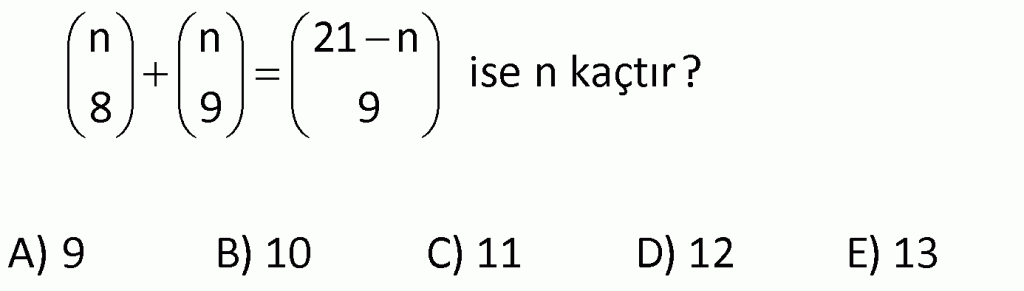
| | | | | |
Çözüm

Alıştırma 4

| | | | | |
Çözüm
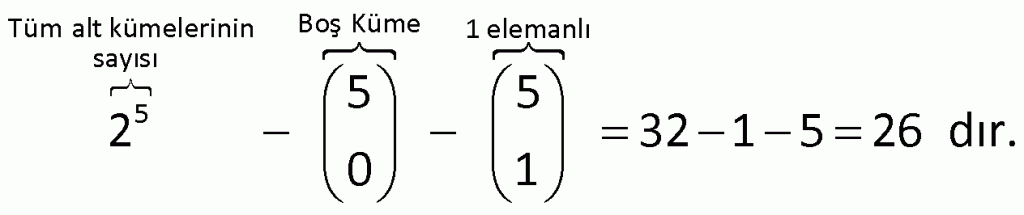
Alıştırma 5

| | | | | |
Çözüm
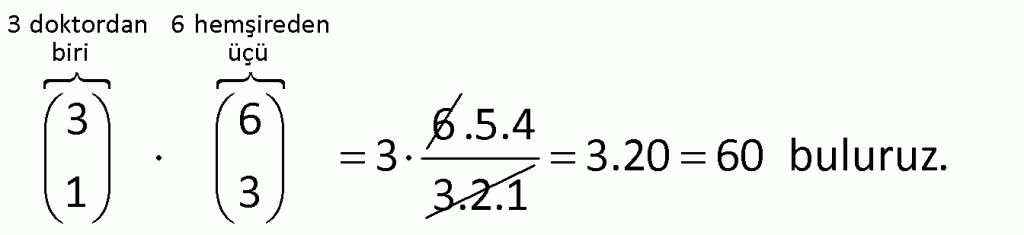
Alıştırma 6

| | | | | |
Çözüm

Alıştırma 7

| | | | | |
Çözüm

Alıştırma 8

| | | | | |
Çözüm

Alıştırma 9

 | | | | |
Çözüm


