Konu ile ilgili Çözümlü Soruları Görmek için Tıkla
Herhangi bir A kümesinden A kümesine tanımlanan her fonksiyona birli işlem denir.
A ⊂ B olmak üzere, A x A kümesinden B kümesine tanımlanan her fonksiyona ikili işlem veya kısaca işlem denir.
İşlemler; +, –, :, x, Δ, Ο gibi simgelerle gösterilir.
İŞLEMİN ÖZELİKLERİ
A kümesinde Ο ve Δ işlemleri tanımlanmış olsun. Buna göre, aşağıdaki 7 özeliği inceleyelim.
1. Kapalılık Özeliği
∀ (Her) a, b ∈ A için a Ο b nin sonucu A kümesinin bir elemanı ise, A kümesi Ο işlemine göre kapalıdır.
2. Değişme Özeliği
∀ (Her) a, b ∈ A için, a Ο b = b Ο a ise, Ο işleminin değişme özeliği vardır.
3. Birleşme Özeliği
∀ (Her) a, b, c ∈ A için a Ο (b Ο c) = (a Ο b) Ο c ise, Ο işleminin birleşme özeliği vardır.
4. Birim (Etkisiz) Eleman Özeliği
∀ (Her) x ∈ A için, x Ο e = e Ο x = x ise, e ye Ο işleminin etkisiz elemanı denir.
e ∈ A ise, Ο işlemine göre A kümesi birim eleman özeliğine sahiptir.
5. Ters Eleman Özeliği
Ο işleminin etkisiz elemanı e olsun.
a ∈ A için, a Ο b = b Ο a = e olacak biçimde bir b varsa b elemanına Ο işlemine göre a nın tersi denir.
a nın tersi b ise genellikle biçiminde gösterilir.
A kümesinin bütün elemanlarının Ο işlemine göre, tersleri A nın elemanı ise, Ο işlemine göre A kümesi ters eleman özeliğine sahiptir.
• Birim elemanın tersi kendisine eşittir.
• Tersi kendisine eşit olan her eleman birim eleman olmayabilir.
6. Dağılma Özeliği
∀ a, b, c ∈ A için,
a Δ (b Ο c) = (a Δ b) Ο (a Δ c) ise,
Δ işleminin Ο işlemi üzerine soldan dağılma özeliği vardır.
(a Ο b) Δ c = (a Δ c) Ο (b Δ c) ise,
Δ işleminin Ο işlemi üzerine sağdan dağılma özeliği vardır.
Δ işleminin Ο işlemi üzerine; hem soldan, hem de sağdan dağılma özelliği varsa Δ işleminin Ο işlemi üzerine dağılma özelliği vardır.
7. Yutan Eleman Özeliği
∀ x ∈ A için, x Ο y = y Ο x = y olacak biçimde bir y varsa y ye Ο işleminin yutan elemanı denir.
y ∈ A ise, Ο işlemine göre A kümesi yutan eleman özeliğine sahiptir.
Yutan elemanın tersi yoktur. Fakat tersi olmayan her eleman yutan eleman değildir.
TABLO İLE TANIMLANMIŞ İŞLEMLER
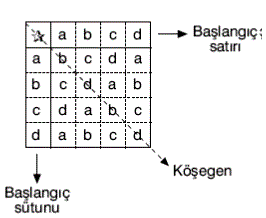
A = {a, b, c, d} kümesinde 
işlemi yukarıdaki tablo ile tanımlanmış olsun.
• b c nin sonucu bulunurken, başlangıç sütununda b, başlangıç satırında c bulunur. Bunların kesiştiği bölgedeki eleman, b c nin sonucudur. Buna göre, b c = a dır.
• Başlangıç satırındaki ve başlangıç sütunundaki elemanların sonuçlarının görüldüğü kısımda A kümesine ait olmayan eleman yoksa A kümesi işlemine göre kapalıdır.
• Sonuçlar kısmı, köşegene göre simetrik ise, işleminin değişme özeliği vardır.
• Tablonun sonuçlar kısmında, başlangıç sütununun ve başlangıç satırının görüldüğü sütunun ve satırın kesişimindeki eleman etkisiz elemandır. Yukarıda tablo ile tanımlanan işleminin etkisiz elemanı d dir.
• Yutan eleman hangi elemanla işleme girerse girsin, sonuç kendisine eşit olur. Bunun için, tablonun sonuçlar kısmında aynı elemandan oluşan satır ve sütun belirlenir. Bulunan yutan elemandır.
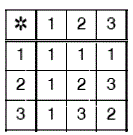Yandaki tablo, A = {1, 2, 3} kümesinde tanımlanan 
işlemine göre düzenlenmiştir.
Buna göre,
işleminin yutan elemanı 1 dir.
işleminin birim (etkisiz) elemanı 2 dir.
MATEMATİK SİSTEMLER
Tanım
A, boş olmayan bir küme olmak üzere, ♦ işlemi A da tanımlı olsun. (A, ♦) ikilisine matematik sistem denir.
Grup
A ≠ Ø olmak üzere, A kümesinde tanımlı ♦ işlemi aşağıdaki dört koşulu sağlıyorsa, A kümesi ♦ işlemine göre bir gruptur.
1. A, ♦ işlemine göre kapalıdır.
2. A üzerinde ♦ işleminin birleşme özelliği vardır.
3. A üzerinde ♦ işleminin birim (etkisiz) elemanı vardır.
4. A üzerinde ♦ işlemine göre her elemanın tersi vardır.
A üzerinde tanımlı ♦ işleminin değişme özelliği de varsa (A, ♦) sistemi değişmeli gruptur.
Halka
A ≠ Ø olmak üzere, A kümesi üzerinde tanımlı Δ ve ♦ işlemleri aşağıdaki üç koşulu sağlıyorsa (A, Δ, ♦) sistemi bir halkadır.
1. (A, Δ) sistemi değişmeli gruptur.
2. A kümesi ♦ işlemine göre kapalıdır.
3. ♦ işleminin Δ işlemi üzerinde dağılma özelliği vardır.
• ♦ işleminin değişme özelliği de varsa (A, Δ, ♦) sistemi değişmeli halkadır.
• ♦ işleminin A kümesinde birim (etkisiz) elemanı da varsa (A, Δ, ♦) sistemine birim halka denir.
Kaynak: www.derscalisiyorum.com
Konu ile ilgili Çözümlü Soruları Görmek için Tıkla
