y Ekseninde Öteleme

Örnek:
Aşağıda f(x) parabolünün 2 birim yukarıya ötelenmesi sonucu oluşan f(x)+2 parabolünün grafiğini görebilirsiniz.
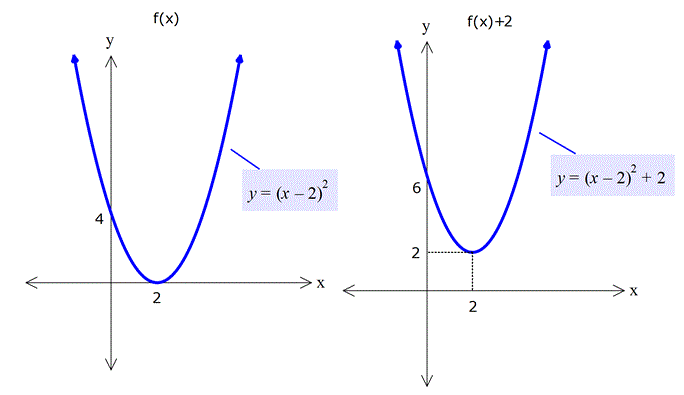
Tüm x değerleri için artık y değerleri 2 birim artmıştır. Örneğin x=0 için y=4 iken y=6 olmuştur. x=2 için y=0 iken y=2 olmuştur.
Örnek:

Çözüm:

x ekseninde Öteleme

Örnek:
Aşağıda f(x) parabolünün 3 birim sağa ötelenmesi sonucu oluşan f(x-3) parabolünün grafiğini ve 2 birim sola ötelenmesi sonucu oluşan f(x+2) parabolünü görebilirsiniz.
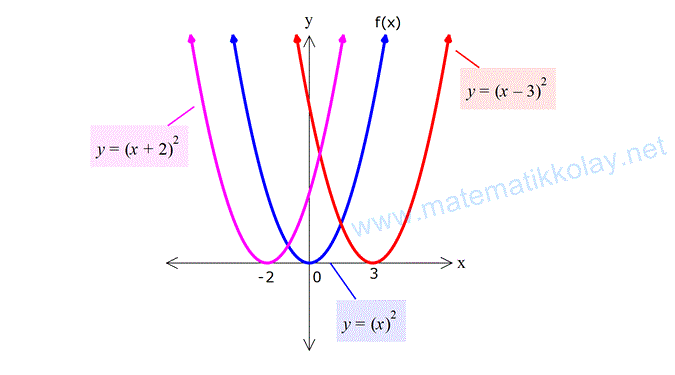
Tüm y değerleri için artık x değerleri şekildeki gibi ötelenmiştir. Örneğin y=0 için x=0 iken, x=-2 olmuştur.
Örnek:
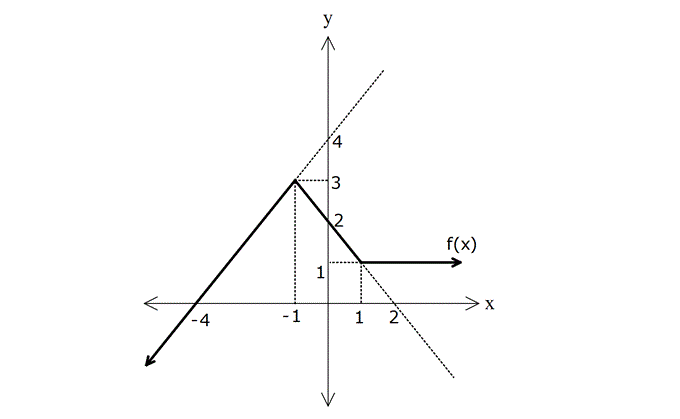
Yukarıda f(x) fonksiyonunun grafiği gösterilmiştir. Buna göre, f(x-2)+1 fonksiyonunun grafiğini çiziniz.
Çözüm:
f(x-2) den dolayı fonksiyon 2 birim sağa ötelecektir.
+1 den dolayı da 1 birim yukarı ötelenecektir.
x ve y eksenindeki ötelemelerde fonskiyonun genel şekli değişmez. Bu sebeple kıvrım noktalarını kullanarak yeni grafiği elde edebiliriz.
f(x)’in içinde bulunan
(-1, 3) noktası (1, 4) noktası olur.
(1, 1) noktası (3,2) noktası olur.
Bu bilgilerle yeni grafiği büyük ölçüde çizebiliriz. Ancak eksenleri kestiği noktaları bulmak için fonksiyonun kuralına ihtiyacımız olabilir.
Bu soruda da fonksiyonun solundaki doğrunun kuralı y=x+4 şeklindedir. 2 birim sağa, 1 birim yukarı ötelenince y=(x-2)+4+1 olur. Yani y=x+3 olur. y eksenini 3 te, x eksenini -3 te kesecektir. O halde aşağıdaki grafiği çizebiliriz.
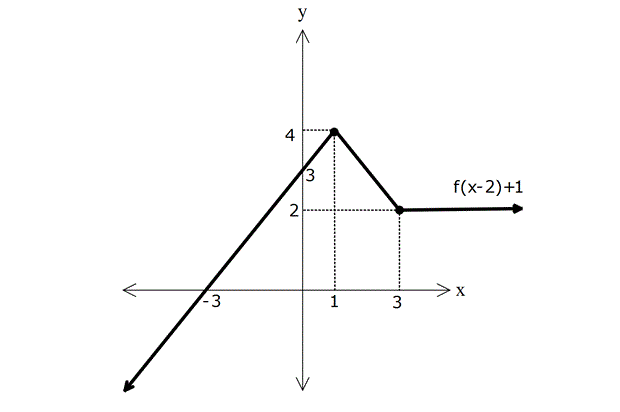
y=k.f(x) Dönüşümü

Örnek:
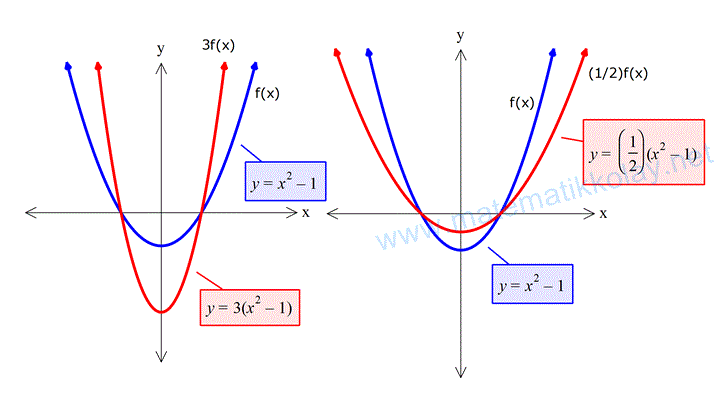
3f(x) olduğunda, aynı x değeri için daha büyük y değeri elde edilmeye başlanmıştır (mutlak değerce).
(1/2)f(x) olduğunda ise daha küçük y değerleri elde edilmiştir (mutlak değerce).
Örnek:
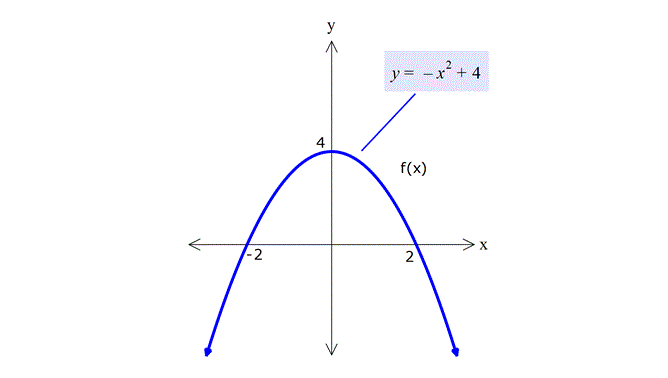
Yukarıda f(x) fonksiyonunun grafiği gösterilmiştir. Buna göre, 2f(x) fonksiyonu eksenleri hangi noktalarda keser?
Çözüm:
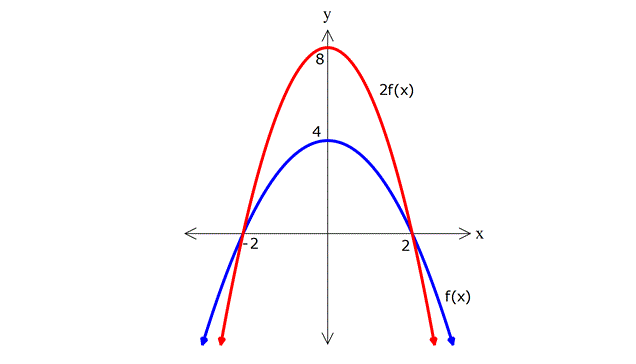
Tüm noktaların ordinatları 2 katına çıkar. x eksenini kestiği noktalarda ordinat 0 olduğundan, bu noktalar değişmez. y ekseni kestiği noktanın ordinatı ise 4’ten 8’e çıkar. Yani, (-2,0), (2, 0) ve (0, 8) noktalarında keser.
y=f(kx) dönüşümü

Örnek:
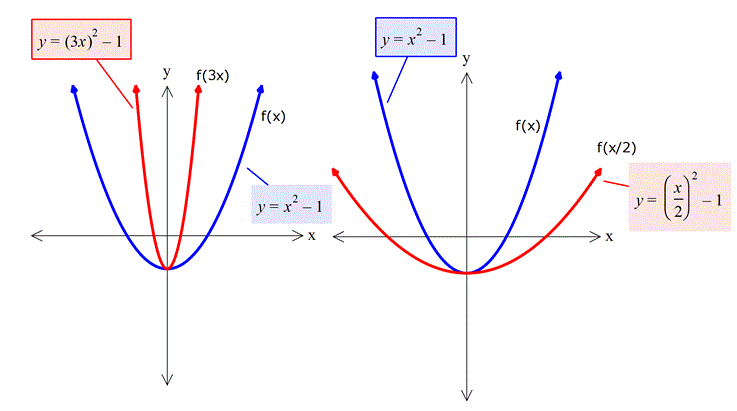
f(3x) olduğunda, aynı y değerine ulaşmak için daha küçük x değeri yeterlidir (mutlak değerce). Bu nedenle fonksiyonun y eksenine yaklaştığını görürüz.
f(x/2) olduğunda ise daha büyük x değerleri gereklidir (mutlak değerce). Bu sebeple fonksiyon y ekseninden uzaklaşmıştır.
Örnek:
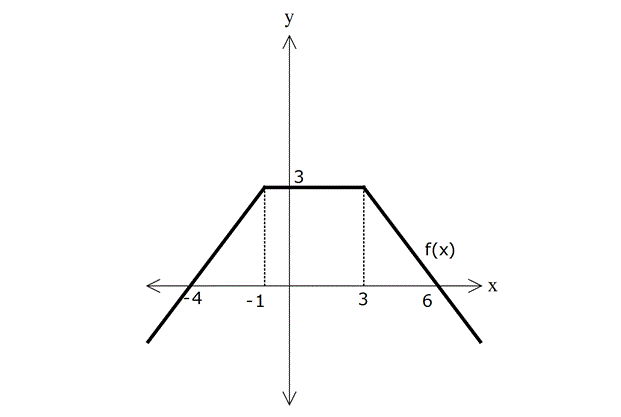
Yukarıda f(x) fonksiyonunun grafiği gösterilmiştir. Buna göre, f(2x) fonksiyonunun grafiğini çiziniz.
Çözüm:
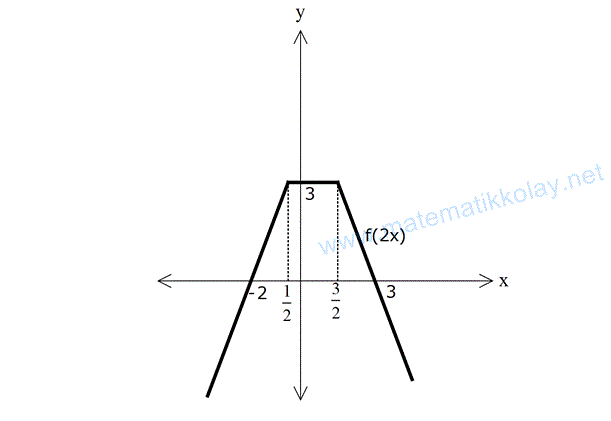
Aynı y değerleri için, x değerlerinin yarısı yeterlidir. Buna göre, aşağıdaki grafiği çizebiliriz.
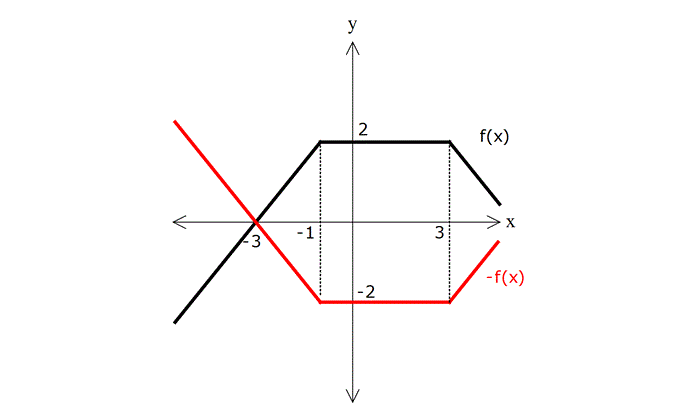
y=-f(x) dönüşümü
Fonksiyonun x eksenine göre yansıması oluşur. Çünkü her bir y değeri, -1 ile çarpılarak x ekseninin diğer tarafına geçer.
Örnek:
y=f(-x) dönüşümü
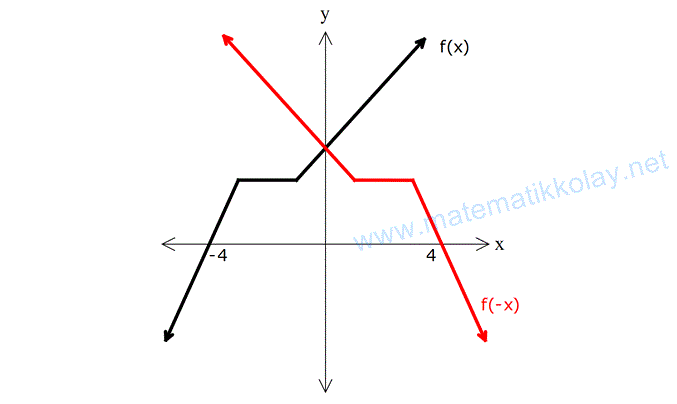
Fonksiyonun y eksenine göre simetrisi alınır. Çünkü x değerleri -1 ile çarpılarak, y ekseninin diğer tarafına geçmiştir.
Örnek:
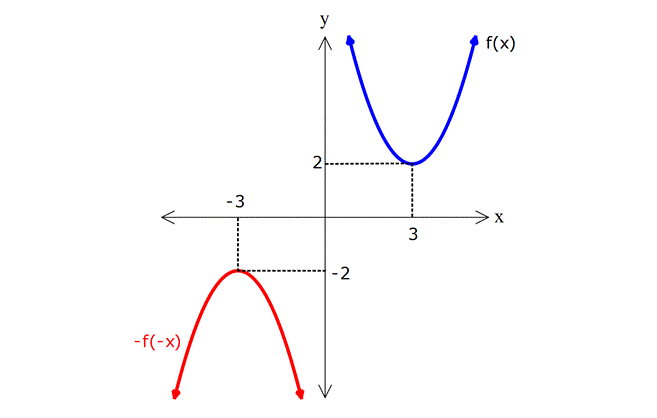
y=-f(-x) dönüşümü
Fonksiyonun orjine göre simetrisi oluşur. Çünkü hem x eksenine göre hem de y eksenine göre simetrisi alınmıştır.
Örnek:
Örnek:
A(1, 2) noktası f(x) eğrisi üzerinde bir noktadır. -f(-x)+3 dönüşümü yapıldıktan sonra bu noktanın koordinatları ne olur?
Çözüm:
-f(-x) ten dolayı orjine göre simetrisi alınır. Yani hem x, hem de y değeri işaret değiştirir.
A(-1, -2) olur.
+3 ten dolayı da y değeri 3 birim artar.
A(-1, 1) olur.
Örnek:
f(x) fonksiyonu ilk önce y ekseninde 2 birim aşağı öteleniyor. Sonra x ekseninde 3 birim sola öteleniyor. En son y eksenine göre simetrisi alınıyor. Bu dönüşümlere göre, yeni fonksiyonu nasıl ifade edebiliriz?
Çözüm:
2 birim aşağı olunca f(x)-2
3 birim sola kaydırılınca f(x+3)-2
y eksenine göre simetrisi alınınca tüm ifade – ile çarpılır. –f(x+3)+2 olur.
Örnek:
f(x) fonksiyonun ilk önce x eksenine göre yansıması alınıyor. Sonra x ekseninde 2 birim sola öteleniyor. Son olarak da 3 birim yukarı öteleniyor. Bu dönüşümlere göre, yeni fonksiyonu nasıl ifade edebiliriz?
Çözüm:
x eksenine göre yansıması f(-x) olur.
2 birim sola kaydırılınca f(-(x+2))=f(-x-2) olur.
3 birim yukarı ötelenince f(-x-2)+3 olur.
Örnek:
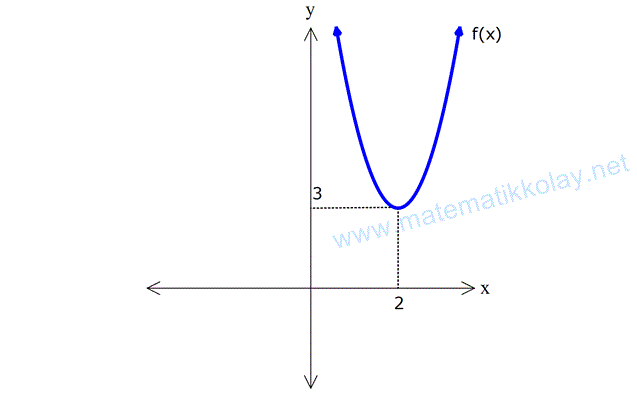
Yukarıda f(x) parabolünün grafiği verilmiştir. Buna göre, f(-x+2) fonksiyonunun grafiğini çiziniz.
Çözüm:
-x ten dolayı y eksenine göre simetrisi alınır.
-x+2=-(x-2) olduğu için x ekseninde 2 birim sağa ötelenir. Buna göre, aşağıdaki grafiği çizebiliriz.
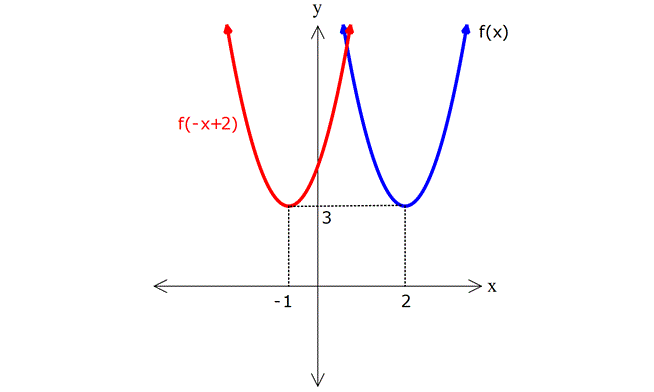
Tepe noktası için, kontrol edelim.
f(2)=3 idi. f(-x+2) fonksiyonunda x=-1 yazarsak, fonksiyonun içi f(3) olur. Dolayısıyla yeni tepe noktasının x=-1 de olması doğrudur.
Örnek:
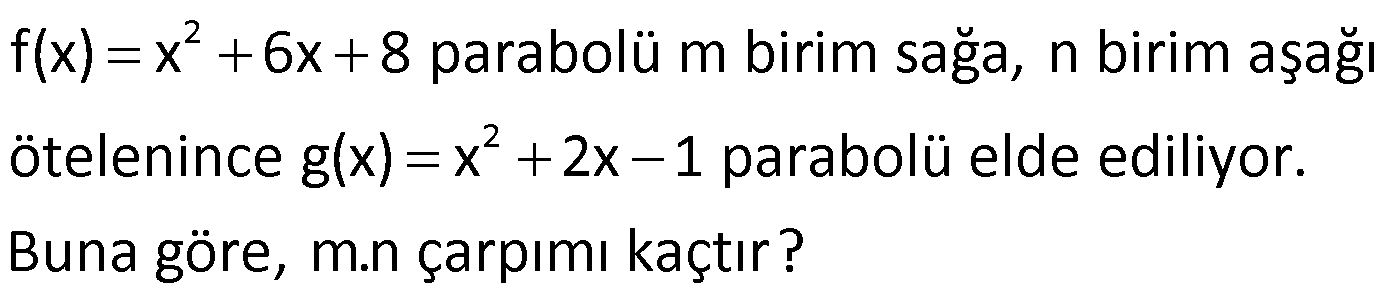
Çözüm:

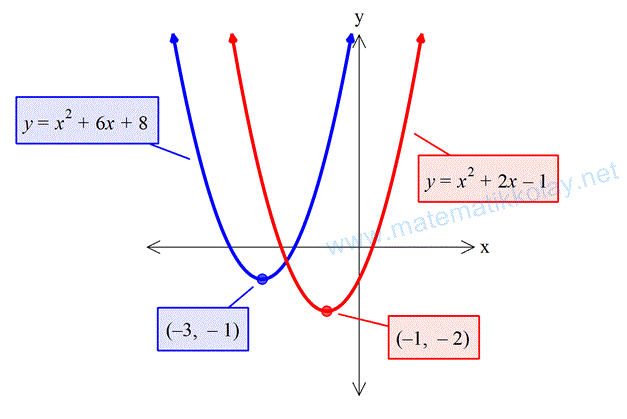
Tek ve Çift Fonksiyonların Grafikleri
Tek fonksiyonların grafikleri orjine göre, çift fonksiyonun grafikleri y eksenine göre simetriktir.
Örnek:
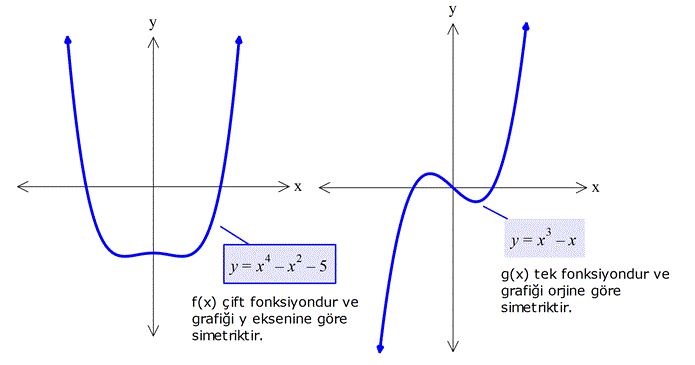
Örnek:
Aşağıdaki fonksiyonlardan hangileri tektir, hangileri çifttir?
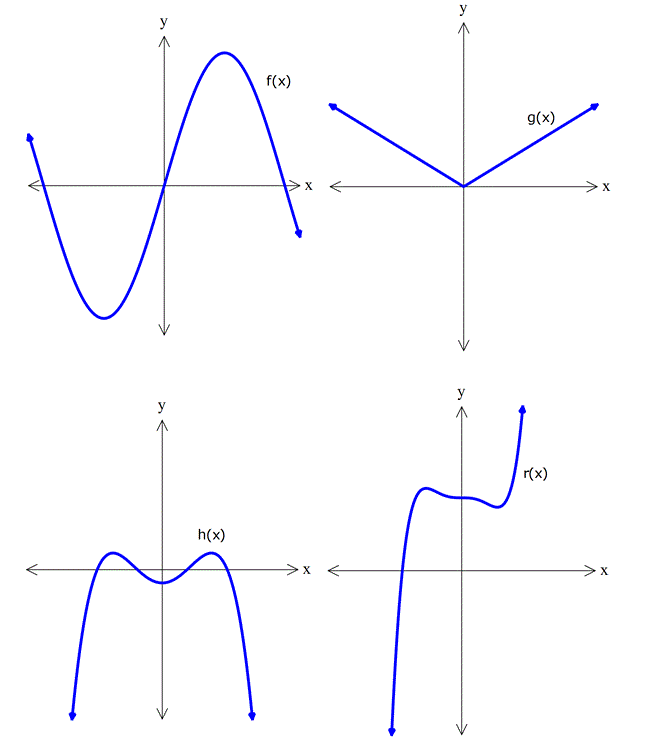
Çözüm:
f(x) orjine göre simetrik olduğundan tek fonksiyondur.
g(x) ve h(x) fonksiyonları y eksenine göre simetrik olduğundan çift fonksiyonlardır.
r(x) fonksiyonu ise ne tek ne de çift fonksiyondur.
Not:
Her x değeri için f(-x)=f(x) ise f(x) çift fonksiyondur.
Her x değeri için f(-x)=-f(x) ise f(x) tek fonksiyondur.
Bir fonksiyon tek ya da çift olmak zorunda değildir.
Polinom fonksiyonlarında tüm x’lerin kuvveti çift olursa fonksiyon çift, tüm x’lerin kuvveti tek olursa fonksiyon tek olur. Tek fonksiyonda sabit terim olmaz.
Örnek:

Çözüm:

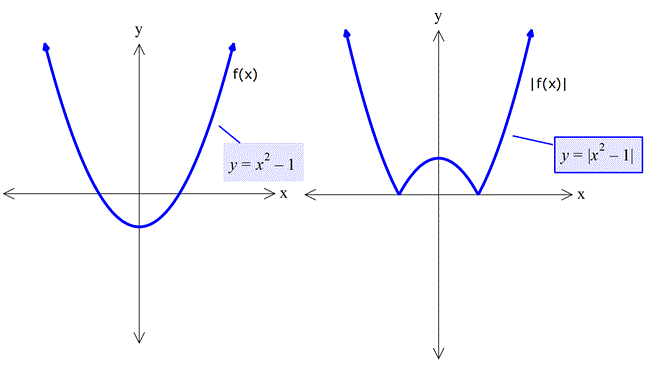
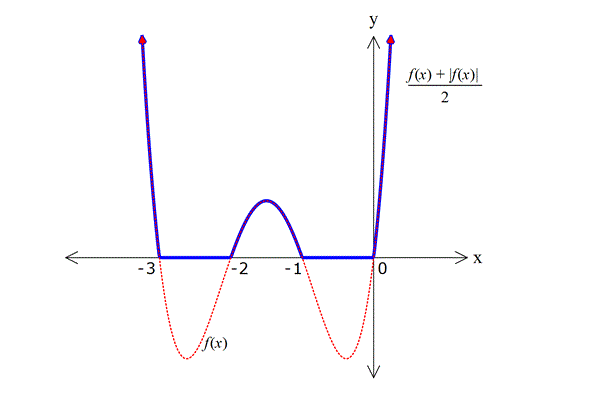
y=|f(x)| dönüşümü (Fen Lisesi için)
x ekseninin altında kalan bölgenin x eksenine göre simetrisi alınır. Diğer kısımlar aynen kalır.
Çünkü f(x) fonksiyonunu mutlak değer içerisine alınca, pozitif olan değerler aynen kalır, negatif olan değerler işaret değiştirir.
Örnek:
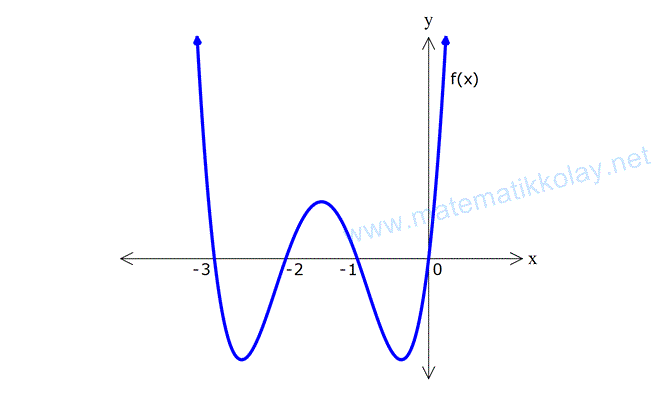
Örnek:
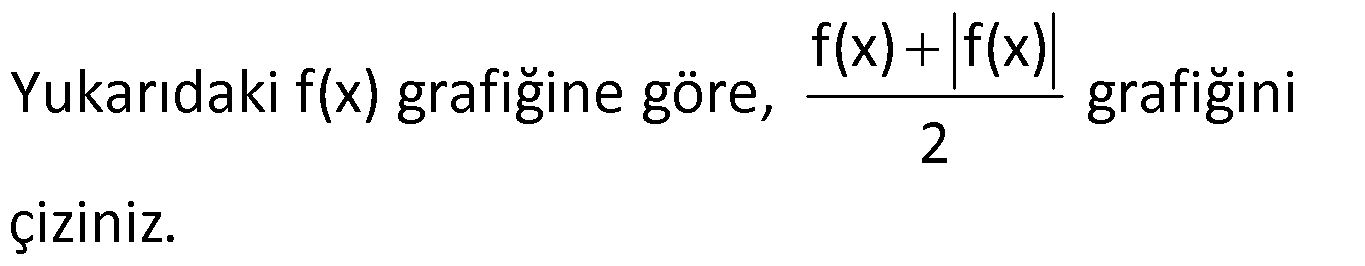
Çözüm:
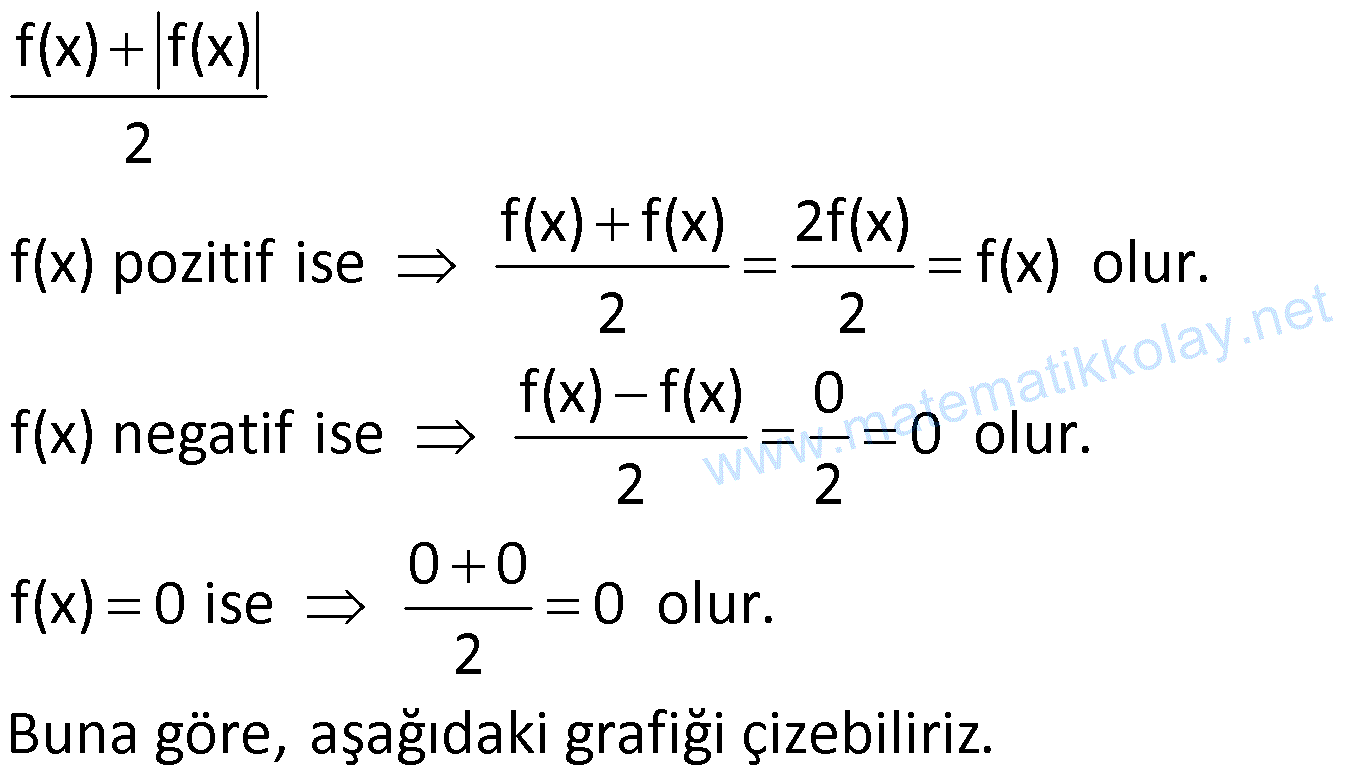
| Çözümlü Sorular veya Çıkmış Sorular için Tıkla |
| Fonksiyonların Dönüşümleri Konu Anlatımını pdf indir |
|
Not: Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
|

