İkinci Dereceden İki Bilinmeyenli
Denklemler
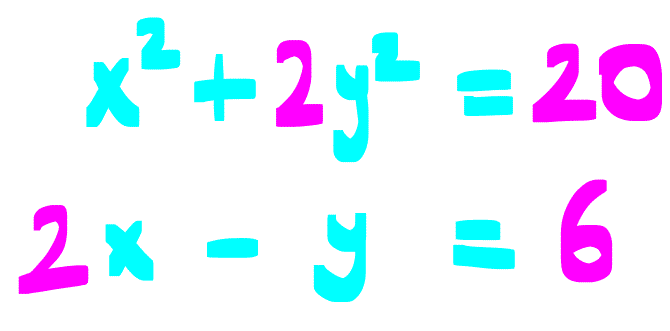


Denklem sistemlerinin çözüm kümesini bulmak
için “yerine koyma metodu” veya “yok etme
metodu” kullanılabilir.
Örnek:

Çözüm:

Örnek:

Çözüm:

Örnek:

Çözüm:

Örnek:

Çözüm:

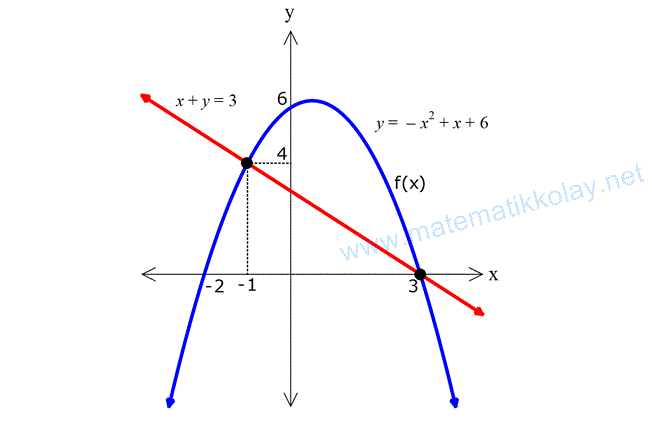
Örnek:
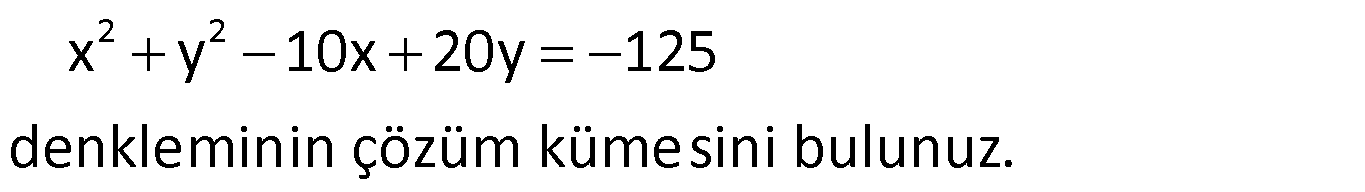
Çözüm:

| Çözümlü Sorular için Tıkla |
| Denklem Sistemleri Konu Anlatımını pdf indir |
|
Not: Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
|
İKİNCİ DERECEDEN İKİ BİLİNMEYENLİ DENKLEM SİSTEMLERİ KONU ANLATIMI www.matematikkolay.net İkinci Dereceden İki Bilinmeyenli Denklemler 2 2 a, b, c, d, e ve f birer gerçek sayı ve a, b, c sayıla – rından en az biri 0 dan farklı olmak üzere ax bxy cy dx ey f 0 şeklindeki deklemlere ikinci dereceden iki bilinme – yenli denklemler denir. Denklemlerden en az bir tanesi ikinci dereceden iki bilinmeyenli denklem olmak üzere en az iki denklemden oluşan sisteme denir. ikinci dereceden iki bilinmeyenli denklem sistemi Denklem sistemlerinin çözüm kümesini bulmak için “yerine koyma metodu” veya “yok etme metodu” kullanılabilir. Örnek: 2 2 2 2 3x 2y 10 x y 5 denklem sisteminin çözüm kümesini bulunuz. Çözüm: 2 2 2 2 2 2 2 2 2 2 2 Değişkenlerden birini yok edecek şekilde hamleler yapalım. 3x 2y 10 2 / x y 5 3x 2y 10 2x 2y 10 5x 20 x 4 x 2 veya x 2 dir. x 2 ise, x 2 2 4 2 2 2 4 y 5 y 1 y 1 veya y 1 dir. x 2 ise, x y 5 y 1 y 1 veya y 1 dir. Çözüm Kümesi {( 1, 2), ( 1, 2), (1, 2), (1, 2)} dir. Örnek: 2 2 x 2y 6 x y 15 denklem sisteminin çözüm kümesini bulunuz. Çözüm: 2 2 2 2 2y 6 2 2 2 2 1.denklemden yararlanarak x’i y cinsinden ifade edelim. x 2y 6 dır. Bunu ikinci denklemde kullanalım. x y 15 2y 6 y 15 4y 24y 36 y 15 3y 24y 21 0 her tarafı 3’e bölelim. y 8y 7 0 (y 7 7 1 )(y 1) 0 y 7 veya y 1 dir. y 7 ise x 2 y 6 14 6 8 dir. y 1 ise x 2 y 6 2 6 4 tür. Çözüm Kümesi {( 8, 7), (4, 1)} dir. Örnek: 2 x y 3 y x 5x 6 denklem sisteminin çözüm kümesini bulup, grafikle gösteriniz. www.matematikkolay.net Çözüm: 2 2 1 3 x y 3 ise y 3 x tir. Bunu ikinci denklemde kullanırsak, 3 x x x 6 x 2x 3 0 olur. (x 1)(x 3) 0 x 1 veya x 3 tür. x 1 ise y 3 x 4 tür. x 3 ise y 3 x 0 dır. Çözüm Kümesi {( 1, 4), (3, 0)} dır. G rafiği çizdiğimizde, doğru ile parabolün kesişim noktaları ( 1, 4) ve (3, 0) olacaktır. Bu durum aşağıda gösterilmiştir. Örnek: 2 2 2x y 3 x xy 2y 5x 16 denklem sisteminin çözüm kümesindeki x değerleri – nin toplamı kaçtır? Çözüm: 2 2 3 2x 3 2x 2 2 2 2 2 2 2 2 2 y 3 2x tir. Bunu ikinci denklemde yazalım. x x y 2 y 5x 16 x x(3 2x) 2(3 2x) 5x 16 x 3x 2x 2(9 12x 4x ) 5x 16 x 3x 2x 18 24x 8x 5x 16 7x 16x 2 0 16 16 Kökler toplamı dir. 7 7 Örnek: 2 2 x y 10x 20y 125 denkleminin çözüm kümesini bulunuz. Çözüm: 2 2 2 2 (x 5) y 10 2 2 Tam kare ifadeler oluşturup, denklemi daha iyi inceleyebiliriz. İlk önce x 10x 25 y 20y 100 0 şeklinde yazabiliriz. (x 5) (y 10) 0 İki tam kare ifadenin toplamı 0 ise, bu nlar ayrı ayrı 0’a eşit olmalıdır. Yani x 5 ve y 10 dur. Çözüm Kümesi {(5, 10)} dur.

