Olasılık Konu Anlatımı

Çözümlü Sorular veya Daha Fazlası için Tıkla

Bir deneyin bütün sonuçlarını eleman kabul eden kümeye örnek uzay ve örnek uzayın her bir alt kümesine olay denir.

Örnek: Zarın bir kez atılmasındaki Örnek Uzay: E={1, 2, 3, 4, 5, 6} dır.

Örnek: 1 madeni para 2 kez havaya atıldığında Örnek Uzay: E={(Y, Y), (Y, T), (T, Y), (T, T)} dır.

Madeni Para Havaya Atıldığında Örnek Uzay

n kere madeni para havaya atıldığında örnek uzayın eleman sayısı ${{2}^{n}}$ dir.

Örnek: Bir madeni para 4 kez havaya atılıyor. Örnek uzay kaç elemanlıdır? İlk ikisinin yazı gelmesi olayı kaç elemanlıdır?

Çözüm için Tıklayınız

Örnek uzay $\displaystyle {{2}^{4}}=16$ elemanlıdır.

İlk ikisinin yazı gelmesi olayının elemanları ise (Y, Y, Y, Y), (Y, Y, Y, T), (Y, Y, T, Y), (Y, Y, T, T) $\displaystyle \Rightarrow$ 4 elemanlıdır.

n Tane Zarın Atılmasında Örnek Uzay

Bir zarın atılmasında örnek uzay 6 elemanlı olduğundan, n tane zarın atılmasında örnek uzay $\displaystyle {{6}^{n}}$ dir.

Örnek: 3 zar havaya atıldığında örnek uzay kaç elemanlıdır?

Çözüm için Tıklayınız

Örnek uzay $\displaystyle {{6}^{3}}=216$ elemanlıdır.

İmkansız ve Kesin Olaylar

Örnek uzayın alt kümelerinden olan boş kümeye imkansız (olanaksız) olay denir.

Örnek: Bir zar atıldığında 7 rakamının gelmesi olayı

Örnek uzayın bütün elemanlarını içeren alt kümesine mutlak (kesin) olay denir.

Örnek: Bir zar atıldığında bir rakam gelmesi olayı

Ayrık Olay

Aynı örnek uzaya ait olup da kesişimleri boş küme ise bu iki olay ayrık olaydır.

Örnek: Zarın 1 gelmesi ile zarın 6 gelmesi ayrık olaylardır.

Örnek: Zarın asal sayı gelmesi ile zarın tek sayı gelmesi ayrık olmayan olaylardır. Çünkü kesişim elemanları vardır (3 ve 5).

Eş Olası Olaylar

Aynı örnek uzaya ait olup da eleman sayıları eşit olan olaylara eş olası olaylar denir.

Örnek: Bir madeni paranın yazı gelmesi ile tura gelmesi eş olası olaylardır.

Bir Olayın Tümleyeni

Bir olayın elemanları dışında kalan örnek uzayın elemanlarının tamamı bu olayın tümleyenidir. Dolayısıyla s(A)+s(A’)=s(E) dir.

Örnek: 5 elemanlı bir kümenin 2 elemanlı alt kümelerinin seçilmesi olayının tümleyeni kaç elemanlıdır?

Çözüm için Tıklayınız

Örnek uzay $\displaystyle {{2}^{5}}=32$ elemanlıdır.

2 elemanlı alt küme sayısı $\displaystyle \left( \begin{array}{l}5\\2\end{array} \right)=\frac{{5.4}}{{2.1}}=10$ dur.

Tümleyeni ise 32-10=22 elemanlı olur.

OLASILIK FONKSİYONU

E örnek uzayının bütün alt kümelerinin oluşturduğu küme ${{E}_{A}}$ olsun.
P : ${{E}_{A}}$ → [0, 1] biçiminde tanımlanan P fonksiyonuna olasılık fonksiyonu denir. A ∈ ${{E}_{A}}$ ise P(A) gerçel sayısına A olayının olasılığı denir.

A olayının olasılığı 0 ile 1 arasındadır. Yani, Her A ∈ K için, 0 ≤ P(A) ≤ 1 dir.

İmkansız olayın olasılığı 0 ve kesin olayın olasılığı 1 dir.

A’, A nın tümleyeni olmak üzere, P(A) + P(A’) = 1 dir.

Olasılık Hesabı

Örnek uzayın her bir elemanın gerçekleşme olasılığı eşit ise, buna eş olumlu uzay denir. Böyle bir uzayda olasılık,

$P(A)=\frac{{s(A)}}{{s(E)}}=\frac{{istenen\text{ durum say }\!\!\imath\!\!\text{ s }\!\!\imath\!\!\text{ }}}{{t\ddot{u}m\text{ durum say }\!\!\imath\!\!\text{ s }\!\!\imath\!\!\text{ }}}$ dır.

Örnek: Bir zar atıldığında tek sayı gelme olasılığını hesaplayalım.

Tüm durumlar $\Rightarrow$ 1,2,3,4,5,6 $\Rightarrow$ 6 tane

İstenen durumlar $\Rightarrow$ 1,3,5 $\Rightarrow$ 3tanedir. O halde,

Olasılık $=\frac{3}{6}=\frac{1}{2}$ dir.

Alıştırma 1

Çözüm için Tıklayınız

Alıştırma 2

Çözüm için Tıklayınız

Alıştırma 3

Çözüm için Tıklayınız

Alıştırma 4

Çözüm için Tıklayınız

A veya B nin Olasılığı

P(A ∪ B) = P(A) + P(B) – P(A ∩ B) dir.

Eğer A ve B ayrık olay ise kesişimleri boş kümedir. Dolayısıyla P(A ∪ B) = P(A) + P(B) dir.

Alıştırma 5

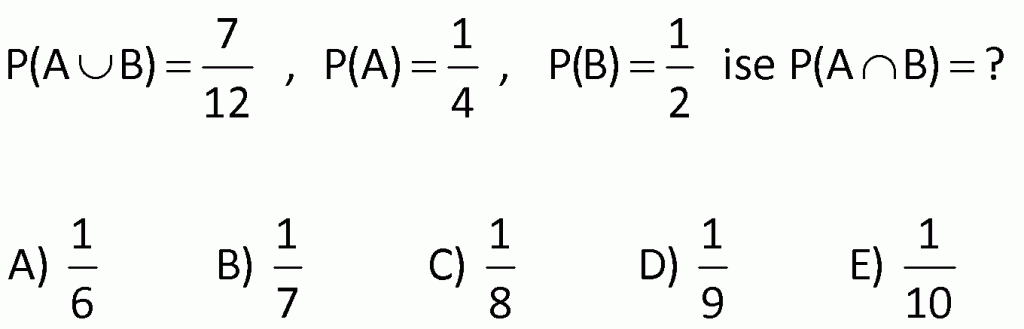
Çözüm için Tıklayınız

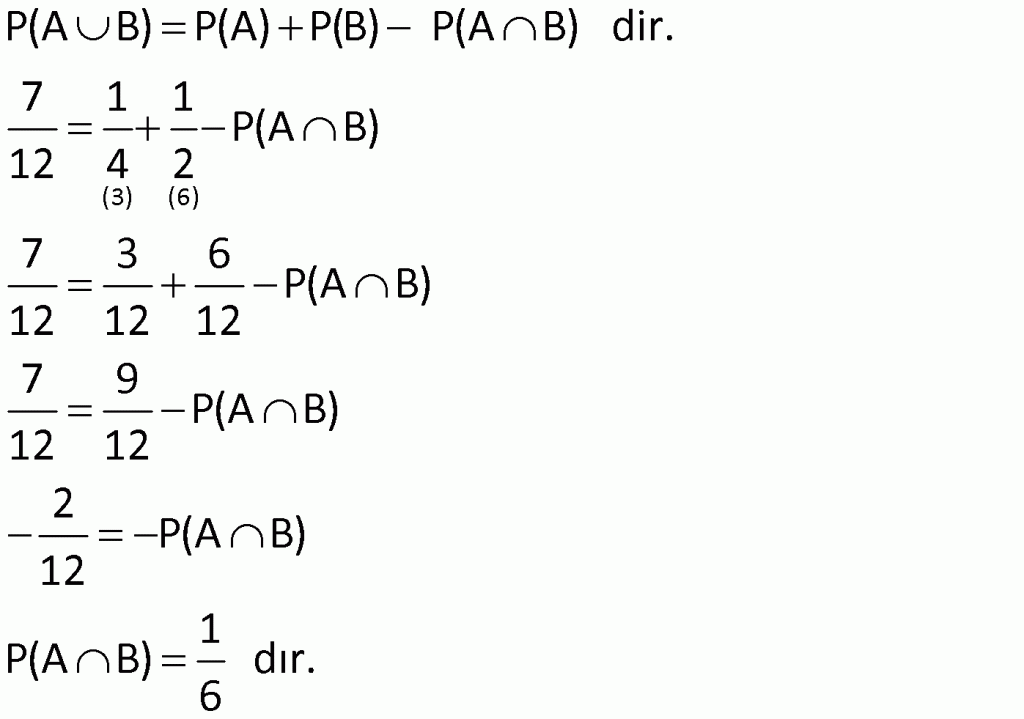
Alıştırma 6

Çözüm için Tıklayınız

Alıştırma 7

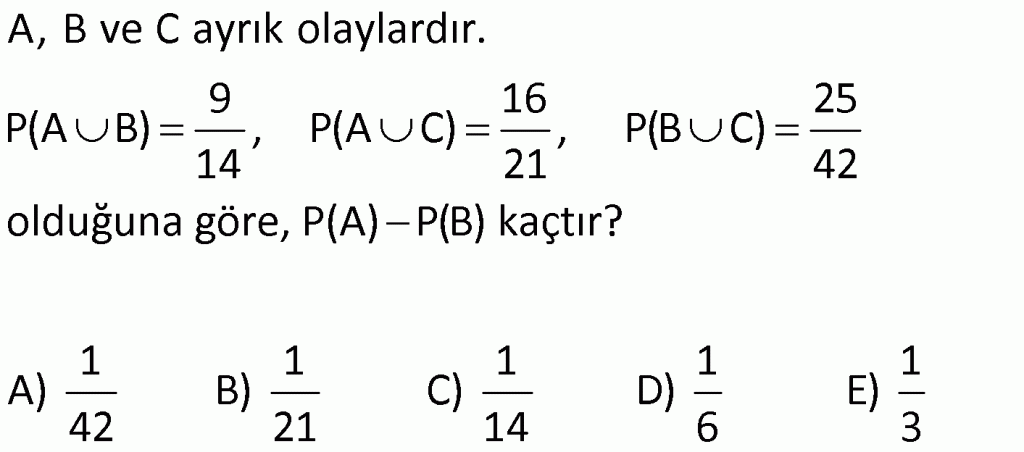
Çözüm için Tıklayınız

Alıştırma 8

Çözüm için Tıklayınız

Konu Bitti. Çözümlü Sorular veya Daha Fazlası için Tıkla

Olasılık genel başlığına gitmek için Tıkla

Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)