21.SORU
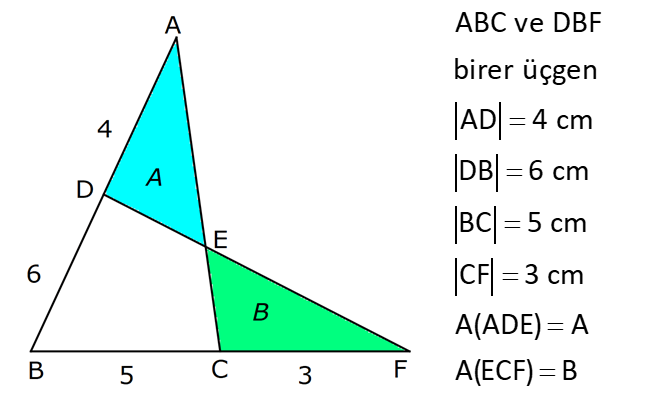
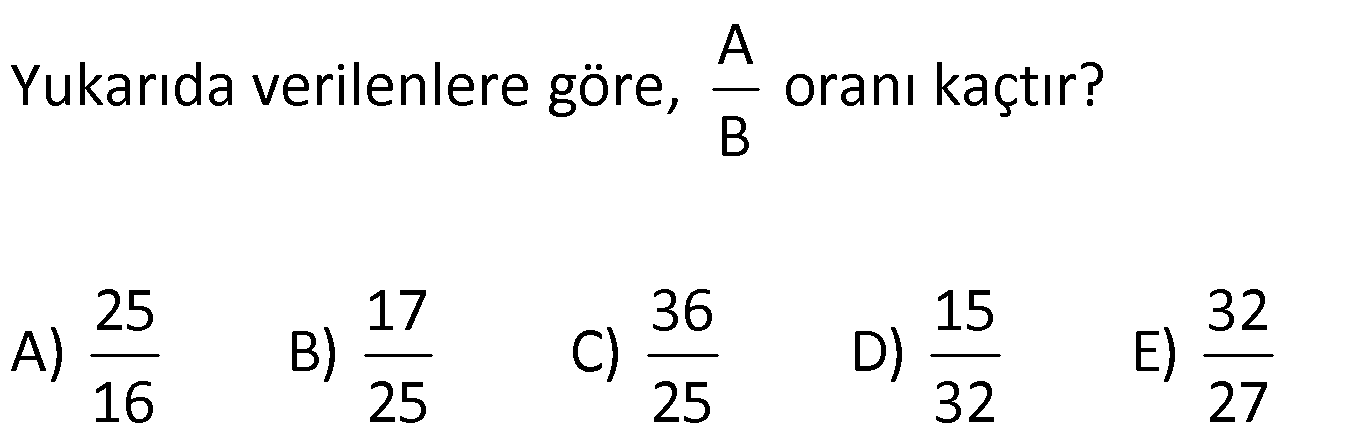
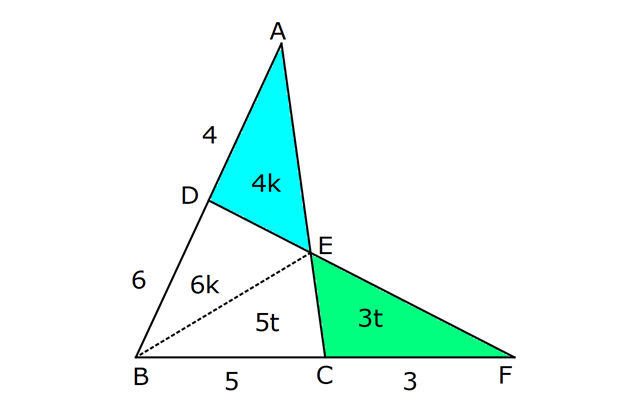
| | | | | |
Çözüm için Tıklayınız.

22.SORU
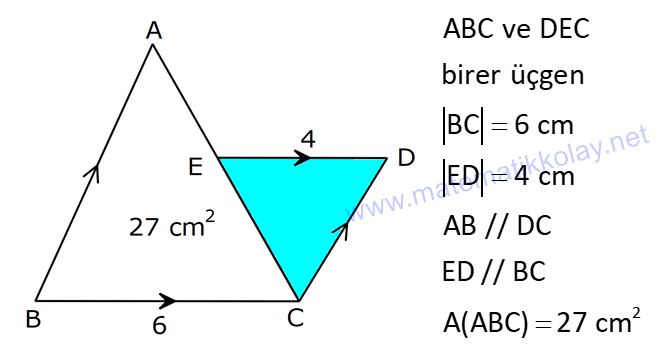
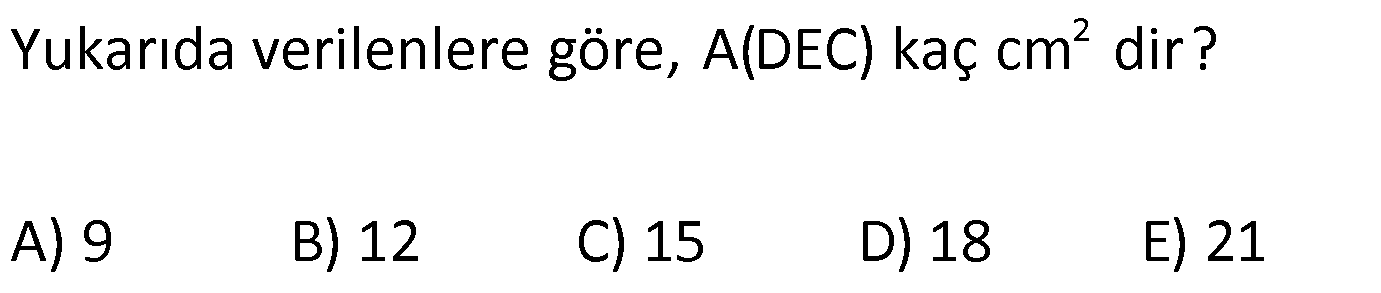
| | | | | |
Çözüm için Tıklayınız.
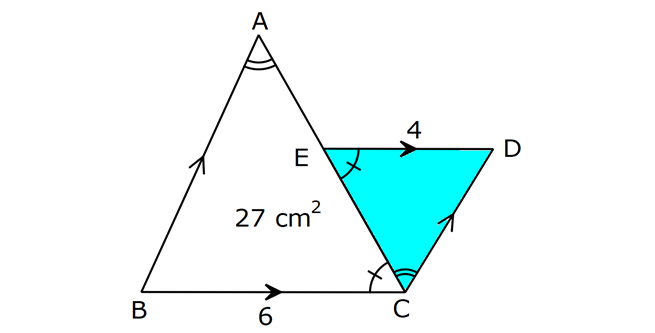
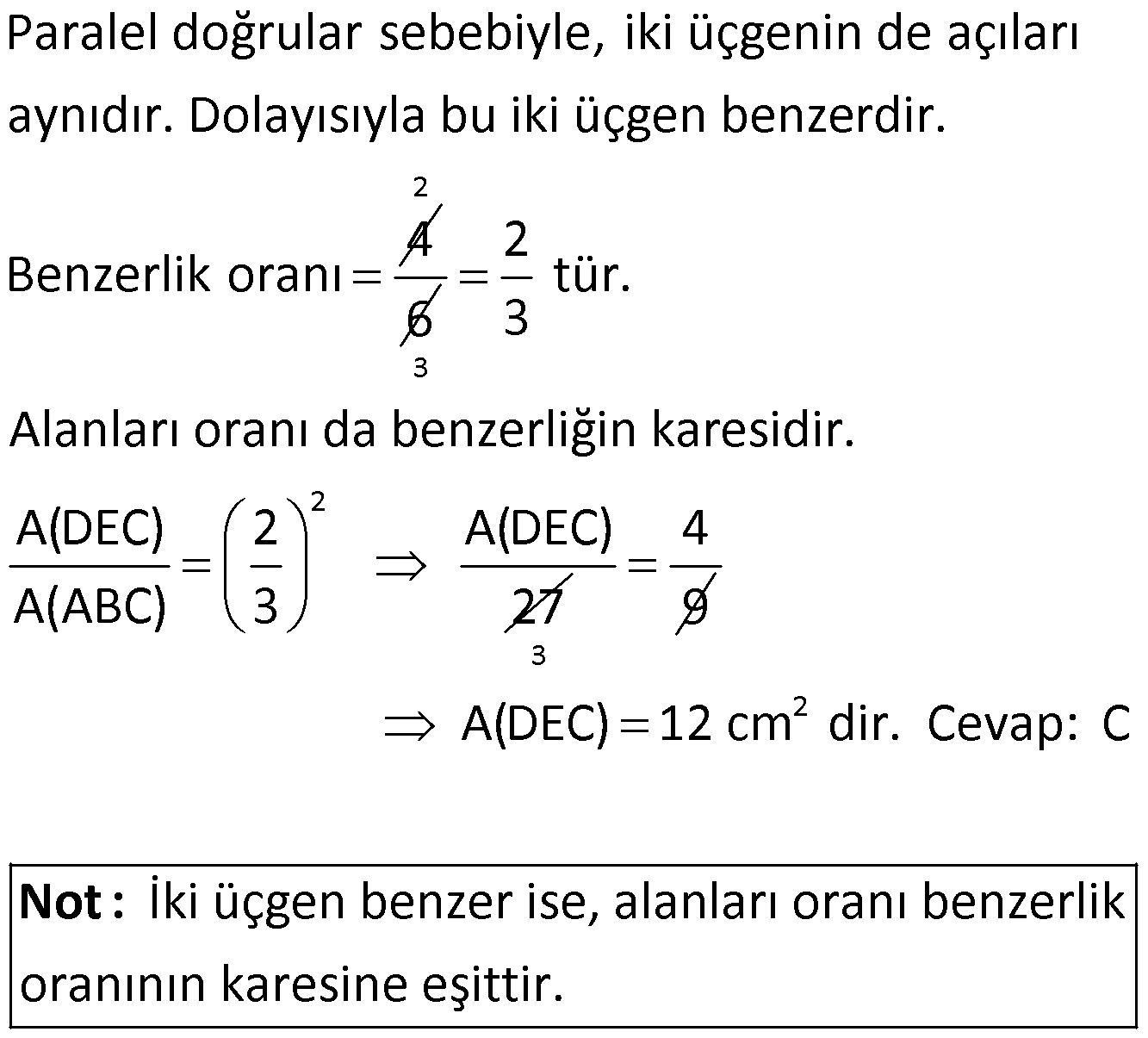
23.SORU
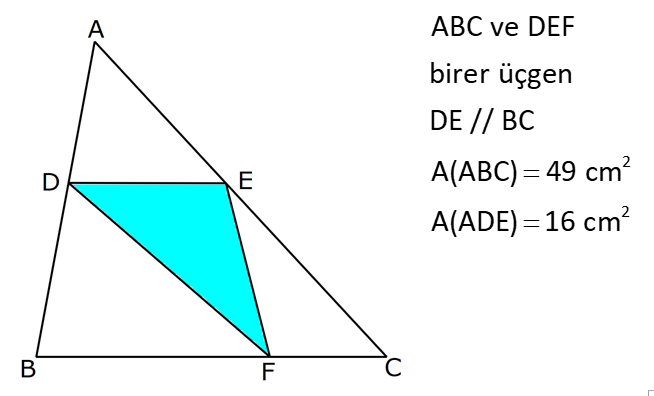
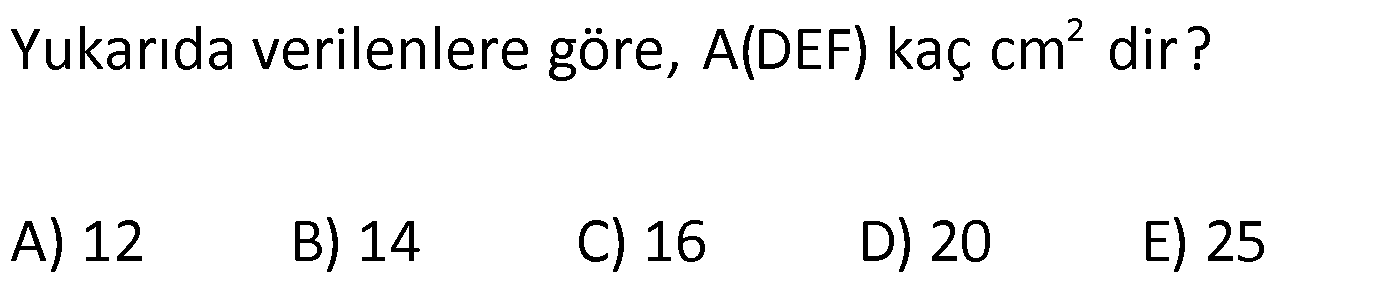
 | | | | |
Çözüm için Tıklayınız.
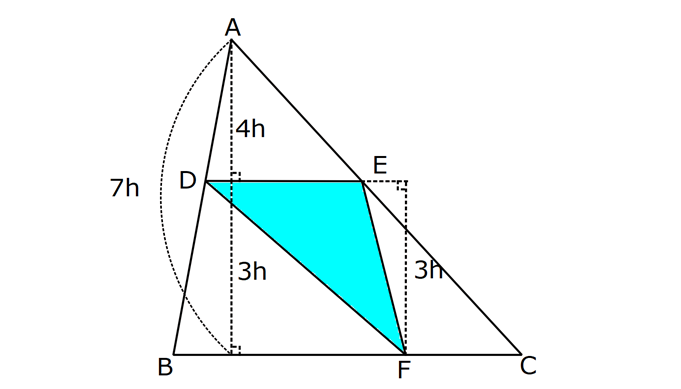

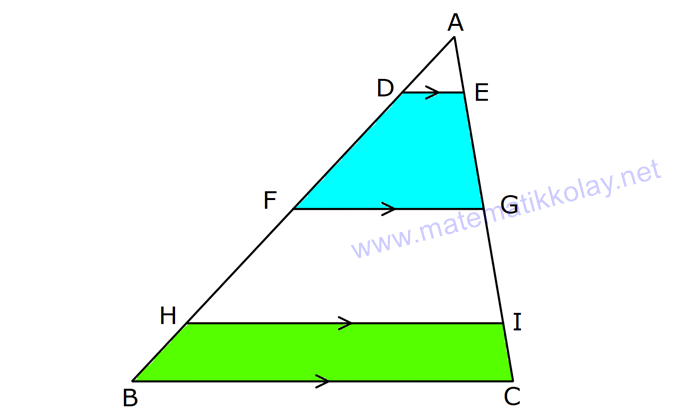
24.SORU
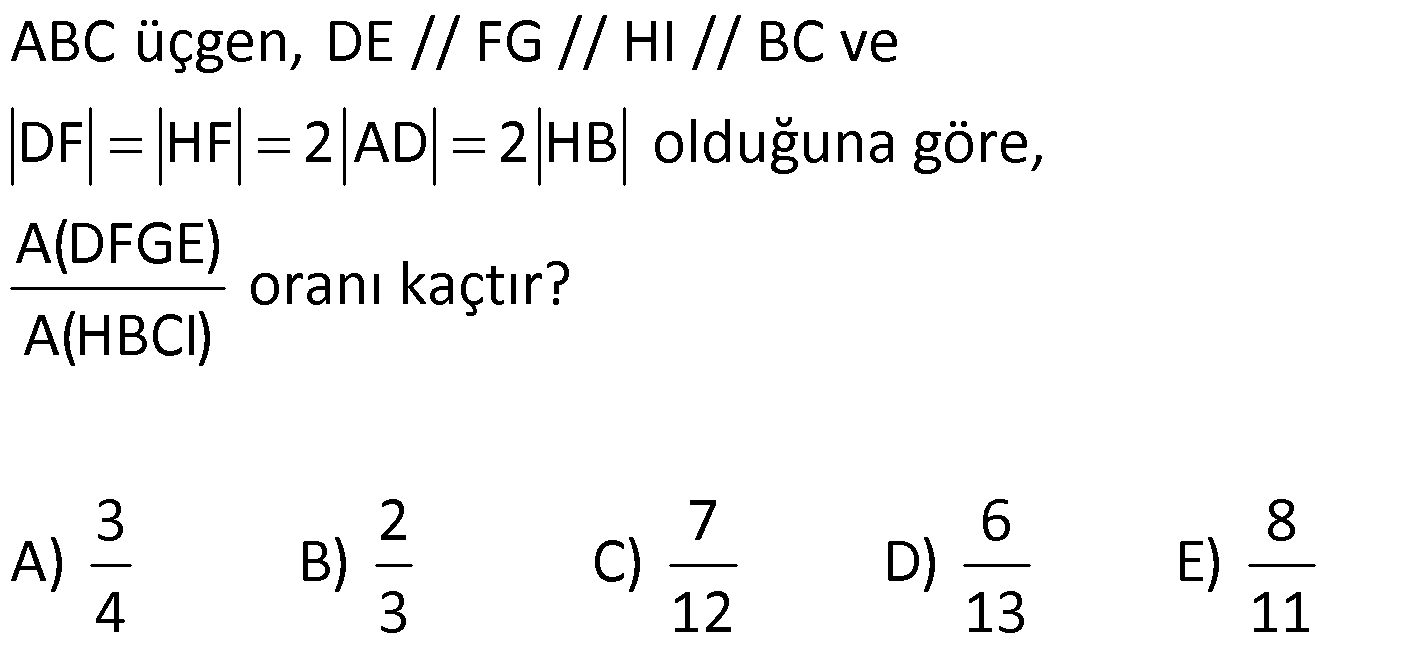
| | | | | |
Çözüm için Tıklayınız.
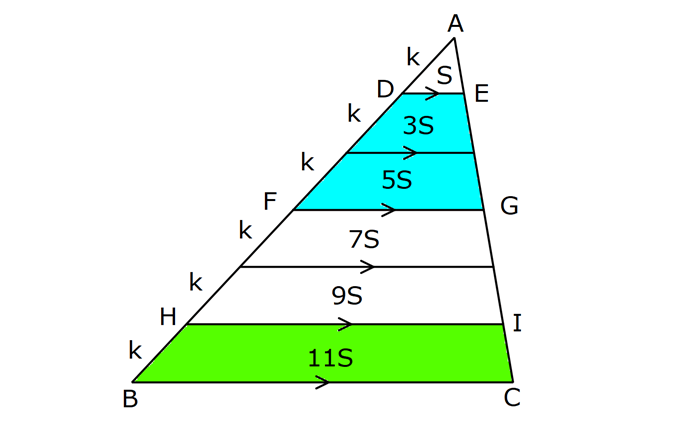

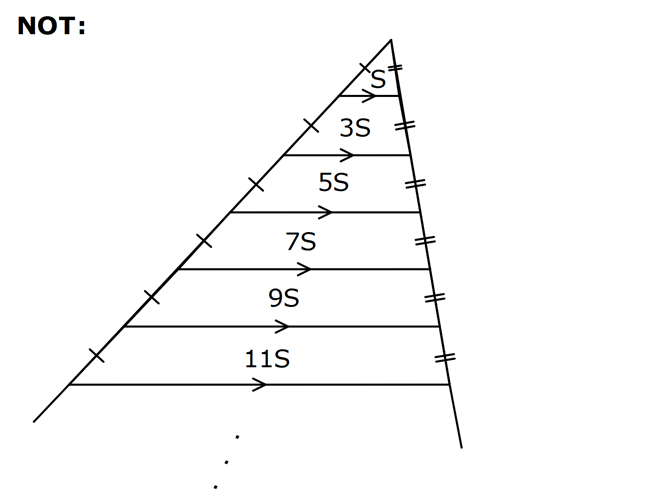
25.SORU
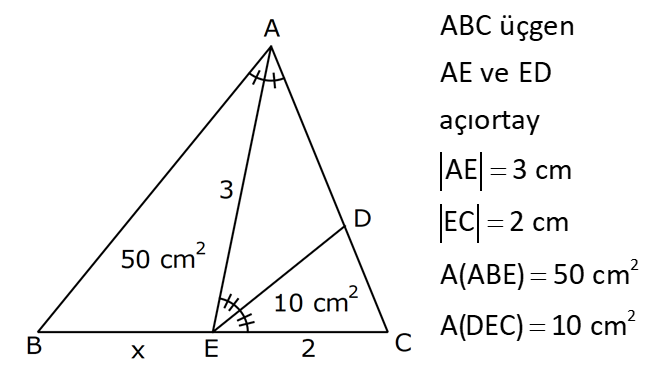
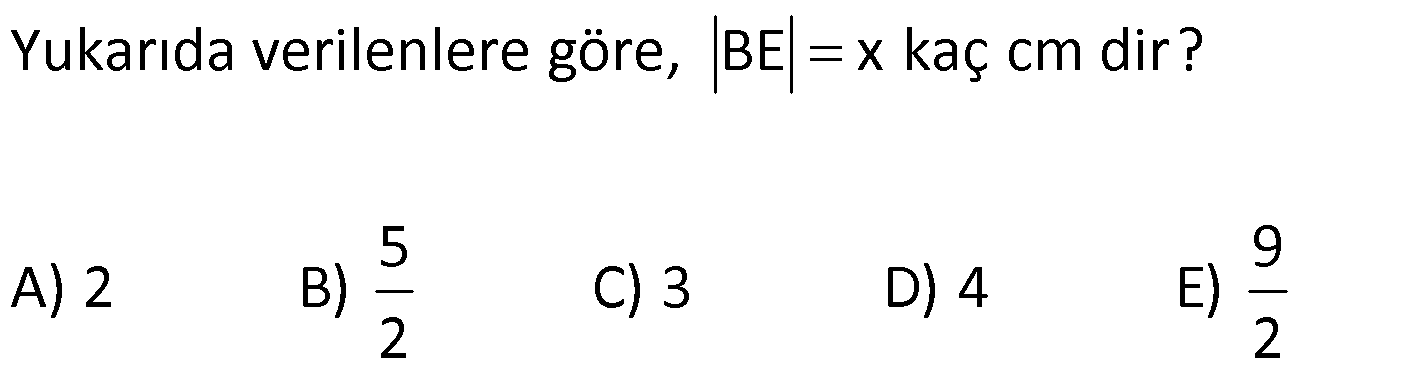
| | | | | |
Çözüm için Tıklayınız.
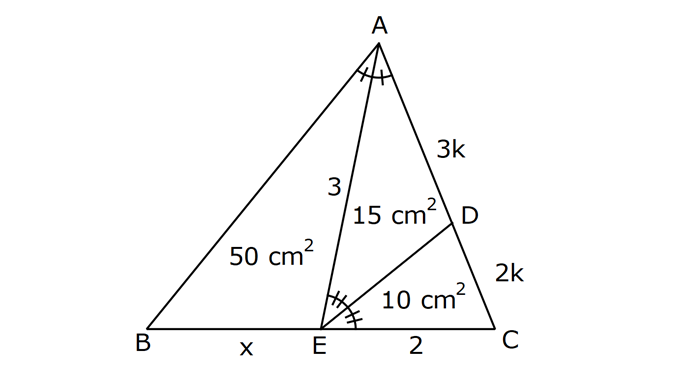

26.SORU (FEN LİSES)
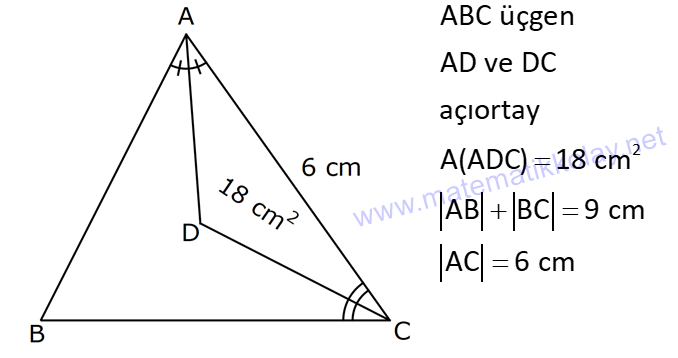
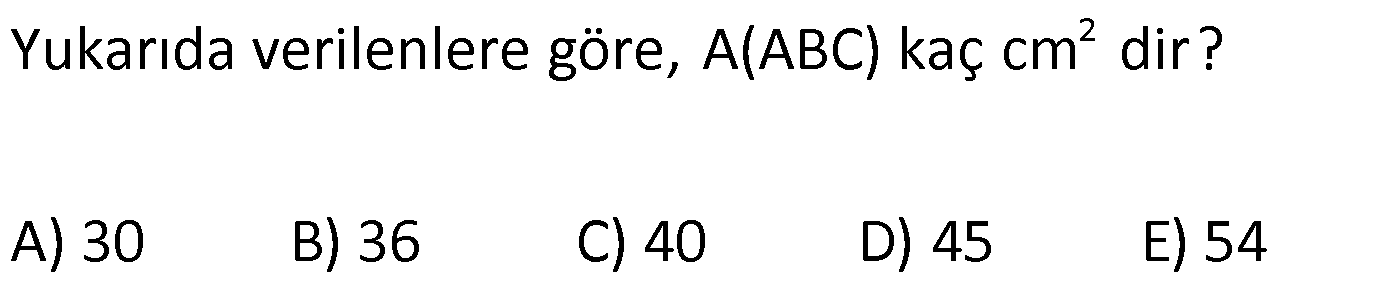
| | | | | |
Çözüm için Tıklayınız.
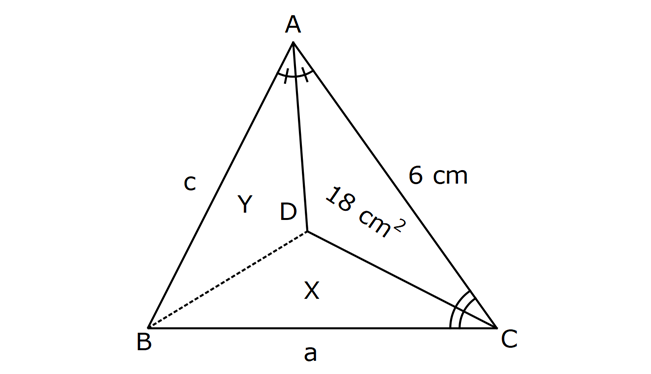

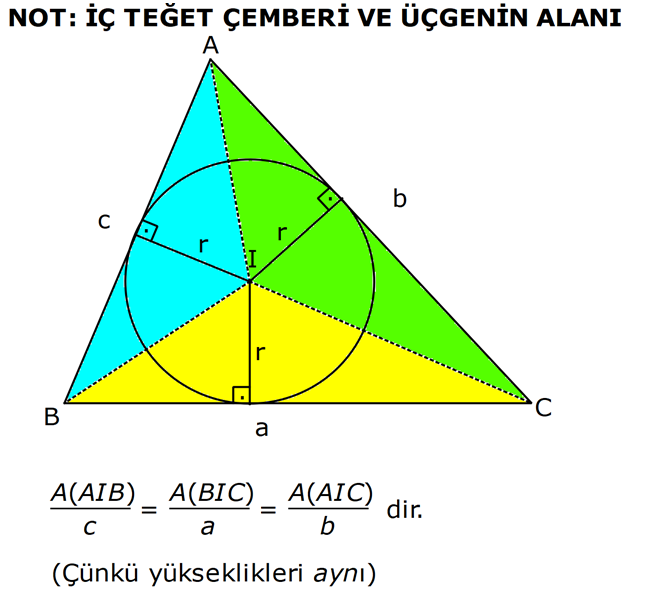
27.SORU (FEN LİSES)
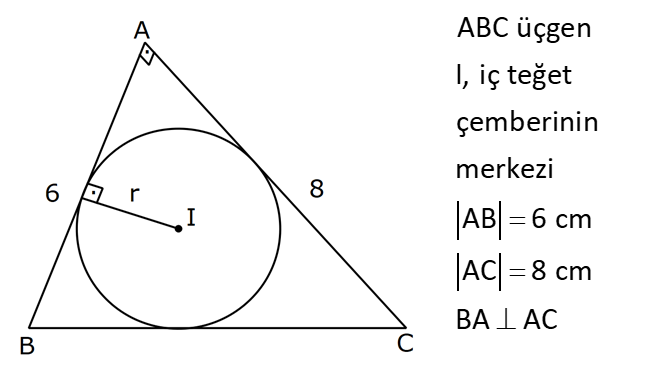
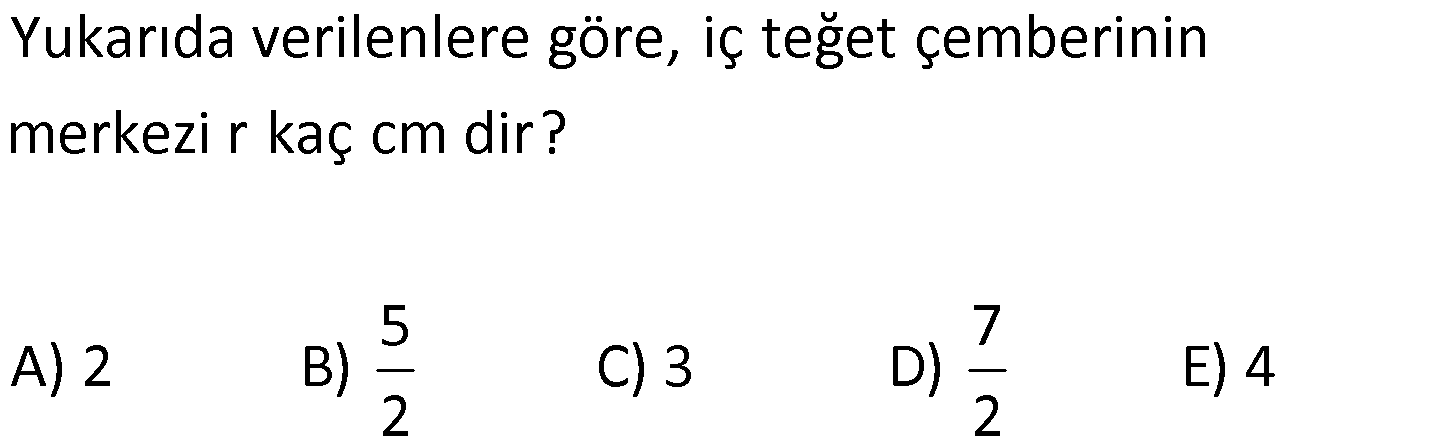
 | | | | |
Çözüm için Tıklayınız.

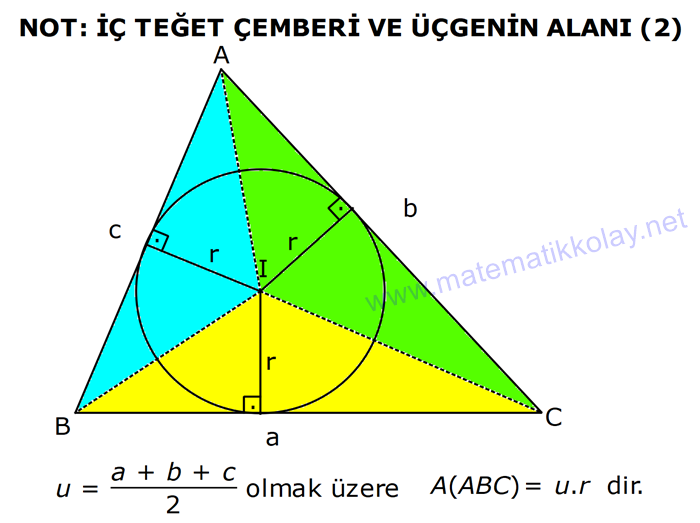
28.SORU (FEN LİSES)
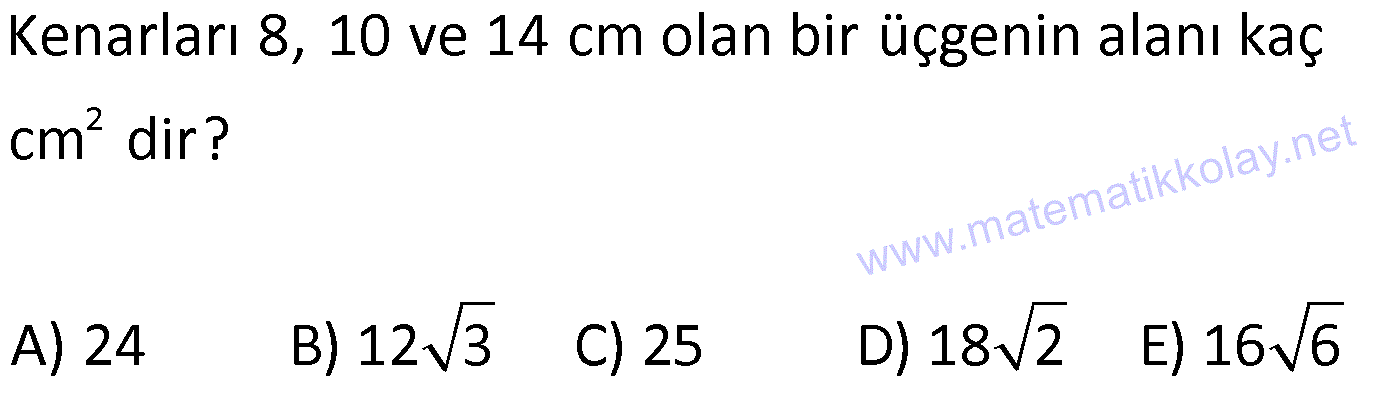
| | | | | |
Çözüm için Tıklayınız.
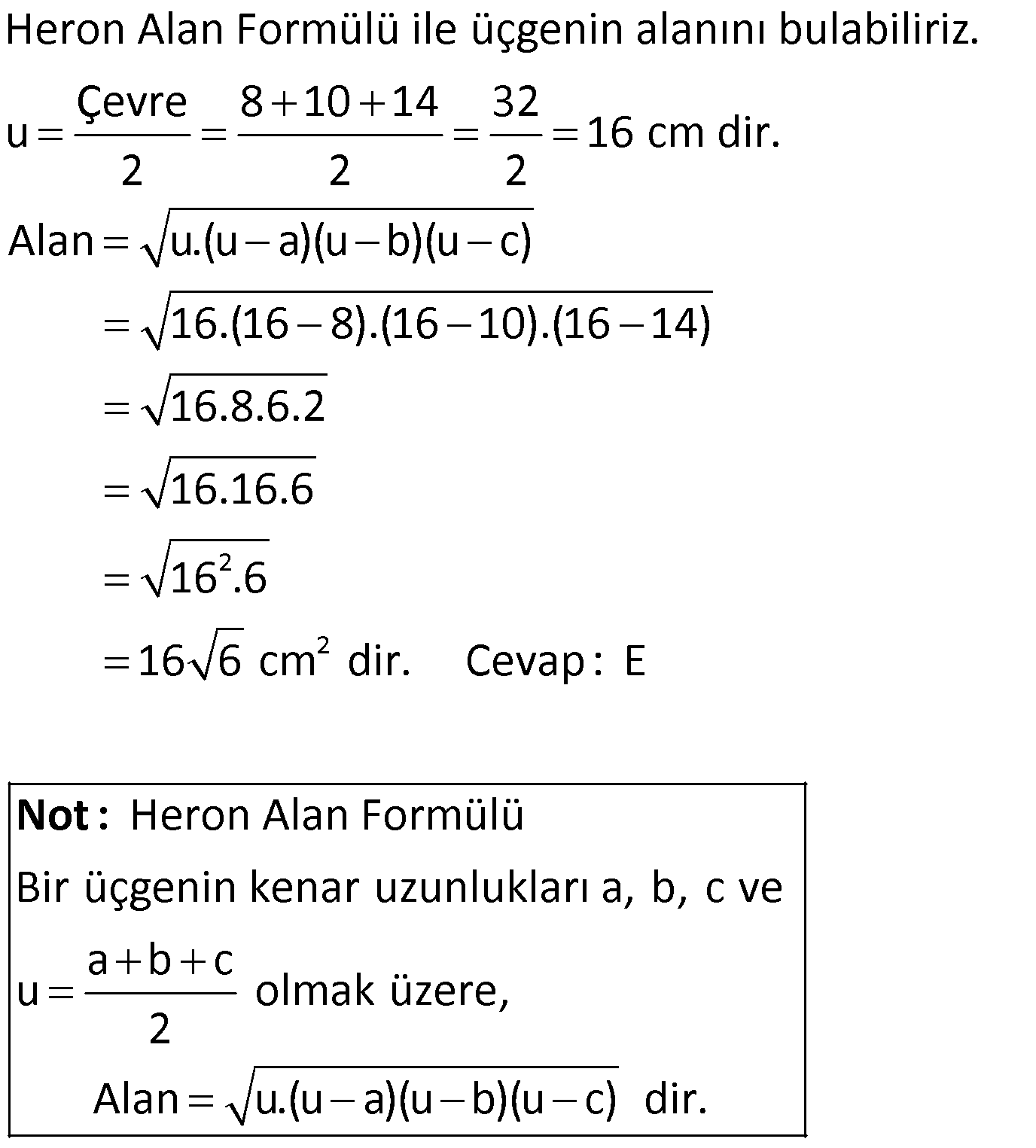
29.SORU (FEN LİSES)
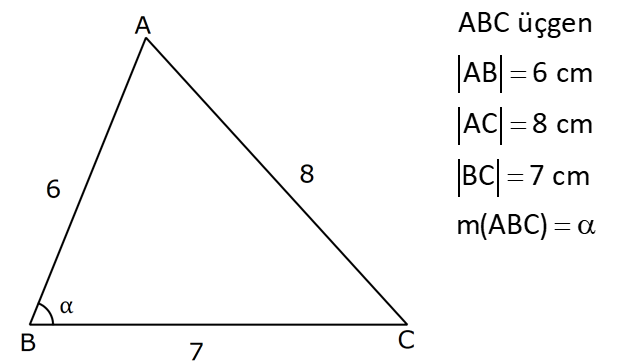
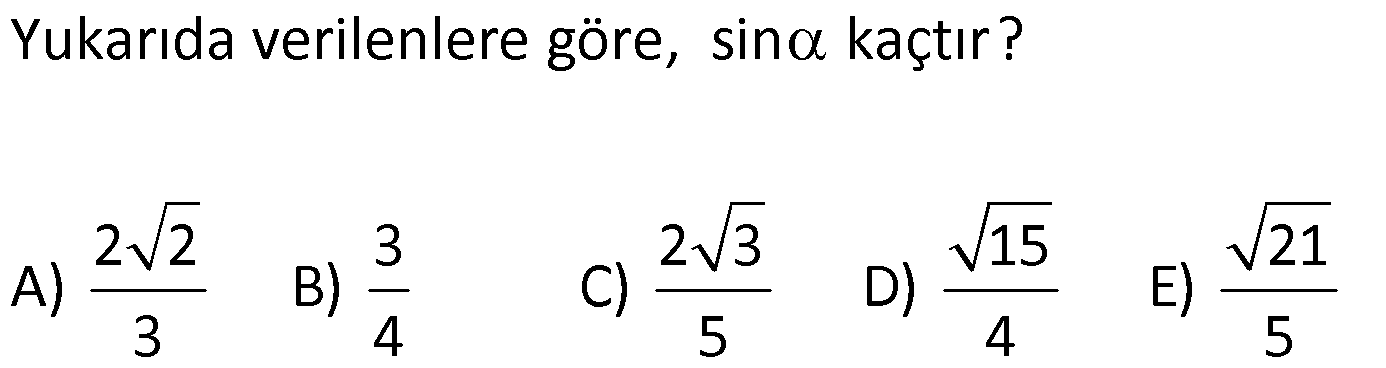
| | | | | |
Çözüm için Tıklayınız.
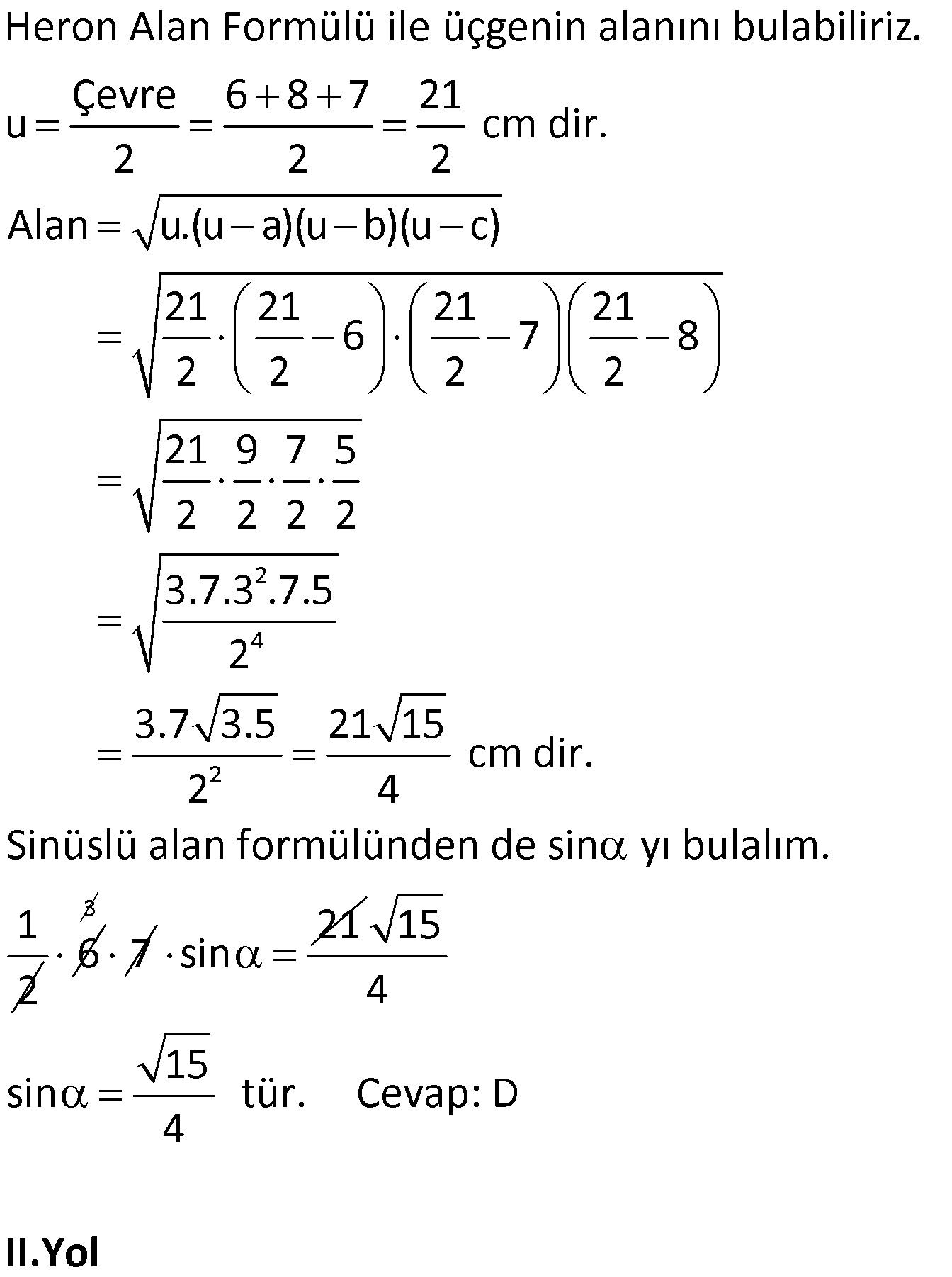
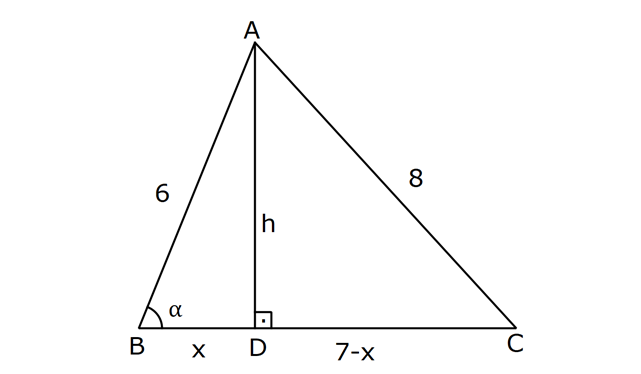
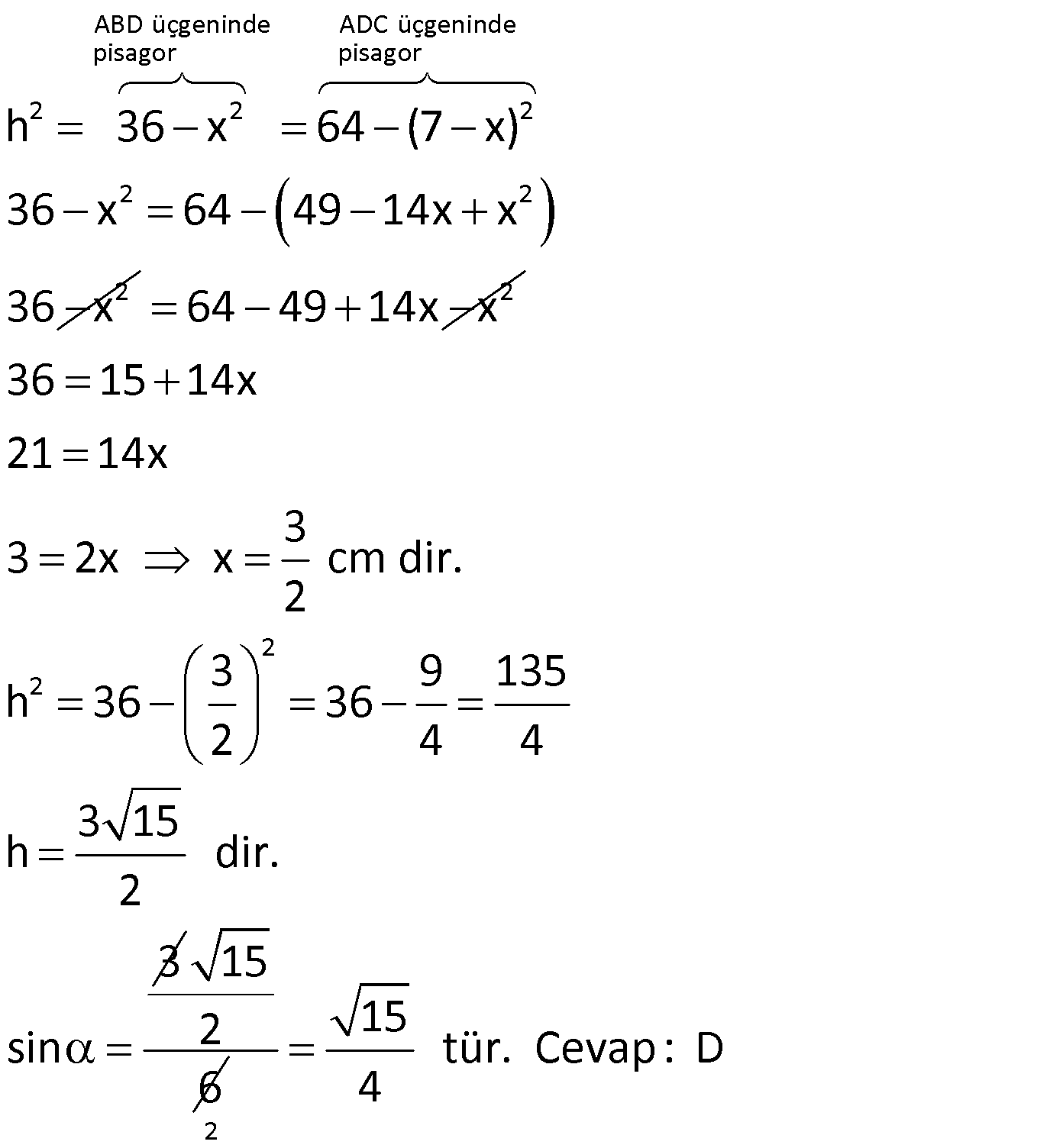


Çok güzel olmuş devamını bekleriz:)
Beğendim Güzel uygulama devamı ve geliştirilmesini bekliyorum.