Çözümlü Sorular veya Çıkmış Sorular için Tıkla
![]() gibi ifadelerin açılımını yaptığımızda terimlerin başına birtakım katsayılar gelir. Örneğin,
gibi ifadelerin açılımını yaptığımızda terimlerin başına birtakım katsayılar gelir. Örneğin, ![]() tür. Terimlerin başında 1,4,6,4,1 katsayıları vardır. Bu katsayıları toplu olarak Pascal üçgeninde görebiliriz.
tür. Terimlerin başında 1,4,6,4,1 katsayıları vardır. Bu katsayıları toplu olarak Pascal üçgeninde görebiliriz.

Yukarıdaki örnek 4.derece bir örnek olduğu için, (4+1).satırdaki katsayılar geldi. Dolayısıyla n.derece bir ifadede (n+1). satırdaki katsayıların gelebileceğini söyleyebiliriz.
Biz bu katsayıları kombinasyon kullanarak da yazabiliriz.
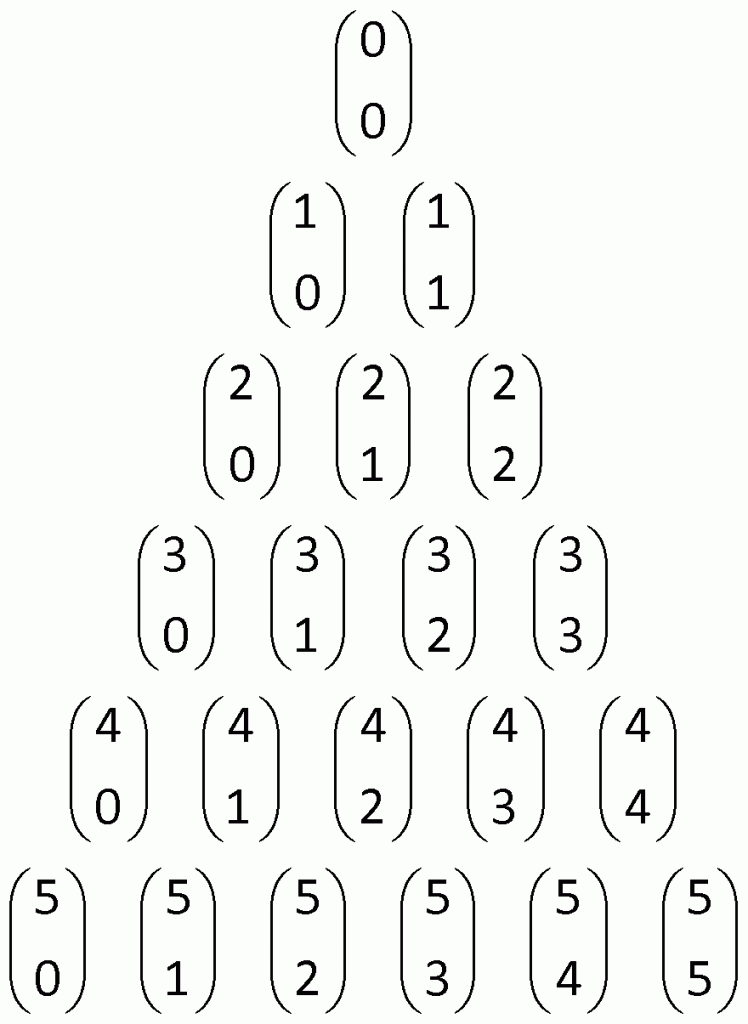
Örnek:
Pascal üçgeninin 8.satırındaki baştan 3.sayı kaçtır?
Cevabı Görmek için Tıklayınız.
8.satırındaki sayılar 7 nin kombinasyonları şeklinde ifade edilir. Baştaki sayı ![]() dır. Dolayısıyla 3.sayı
dır. Dolayısıyla 3.sayı ![]() olacaktır.
olacaktır.
![]() dir.
dir.
Binom Özdeşliği
Pascal üçgenine dikkat edersek, her bir sayı üstündeki iki sayının toplamı ile oluşmuştur. Mesela 4+6=10 u oluşturmuştur.
Bunu kombinasyon ile ifade edersek ![]() ü oluşturmuştur. Bu durumu
ü oluşturmuştur. Bu durumu
![]() şeklinde genelleştirebiliriz. Bu özdeşliğin adı da Binom Özdeşiliği dir.
şeklinde genelleştirebiliriz. Bu özdeşliğin adı da Binom Özdeşiliği dir.
Örnek:
![]()
Çözüm
![]() tir.
tir.
Binom Katsayıları ile Alt küme Sayısı Arasındaki Benzerlik
![]() in açılımındaki katsayılar, n elemanlı bir kümenin 0, 1, 2, … , n elemanlı alt küme sayıları ile aynıdır. Mesela,
in açılımındaki katsayılar, n elemanlı bir kümenin 0, 1, 2, … , n elemanlı alt küme sayıları ile aynıdır. Mesela,
![]() ün açılımındaki kat sayılar 1, 3, 3 ,1 şeklindedir. 3 elemanlı bir kümenin 0 elemanlı alt küme sayısı
ün açılımındaki kat sayılar 1, 3, 3 ,1 şeklindedir. 3 elemanlı bir kümenin 0 elemanlı alt küme sayısı ![]() =1 dir. 1 elemanlı alt küme sayısı
=1 dir. 1 elemanlı alt küme sayısı ![]() =3 tür. 2 elemanlı alt küme sayısı
=3 tür. 2 elemanlı alt küme sayısı ![]() =3 tür. 3 elemanlı alt küme sayısı da
=3 tür. 3 elemanlı alt küme sayısı da ![]() =1 dir.
=1 dir.
Bir kümenin tüm alt kümelerinin ![]() tane olduğunu biliyoruz. Dolayısıyla
tane olduğunu biliyoruz. Dolayısıyla
![]() dir.
dir.
Alıştırma 1
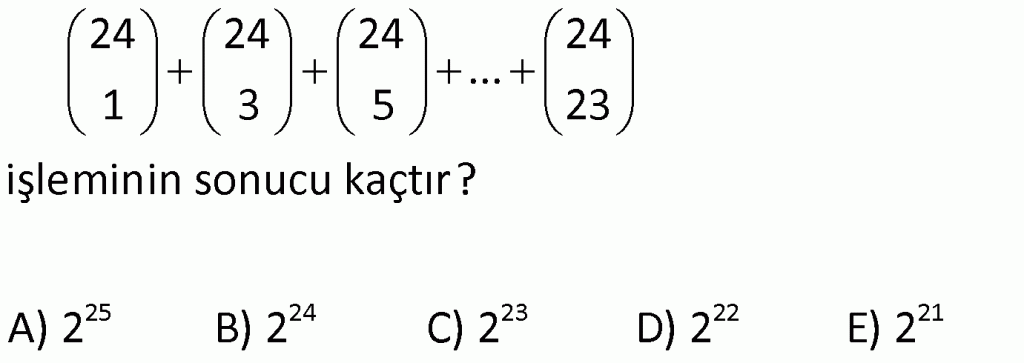
| | | | | |
Çözüm

Binom Açılımı
![]()
şeklinde x’in azalan kuvvetlerine göre yazılmasına binom açılımı denir.
Örnek: ![]() in binom açılımını yapınız.
in binom açılımını yapınız.
Çözüm
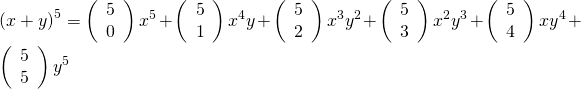
![]()
Örnek: ![]() ün binom açılımını yapınız.
ün binom açılımını yapınız.
Çözüm
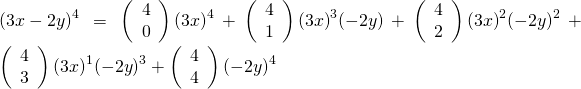
![]()
![]() dir.
dir.
Kural:
![]() açılımında n + 1 tane terim vardır.
açılımında n + 1 tane terim vardır.
![]() ifadesinin açılımındaki sabit terimi bulmak için x ile y yerine 0 yazılır.
ifadesinin açılımındaki sabit terimi bulmak için x ile y yerine 0 yazılır.
![]() ifadesinin kat sayılarının toplamı x ile y yerine 1 yazılarak bulunur.
ifadesinin kat sayılarının toplamı x ile y yerine 1 yazılarak bulunur.
Örnek:
![]() ifadesindeki terim sayısını, sabit terimi ve katsayılar toplamını bulunuz.
ifadesindeki terim sayısını, sabit terimi ve katsayılar toplamını bulunuz.
Çözüm
Derecesi 10 olduğundan 11 terim vardır.
Sabit terimi ise ![]() dur.
dur.
Katsayılar toplamı ise ![]() dir.
dir.
Kural:
![]() ifadesi x’in azalan kuvvetlerine göre açıldığında baştan (r+1). terim
ifadesi x’in azalan kuvvetlerine göre açıldığında baştan (r+1). terim ![]() dir.
dir.
Örnek:
![]() ifadesi x’in azalan kuvvetlerine göre açıldığında baştan 4.terim ne olur?
ifadesi x’in azalan kuvvetlerine göre açıldığında baştan 4.terim ne olur?
Çözüm
![]()
![]() tür. Buna göre,
tür. Buna göre,
![]()
![]()
![]() buluruz.
buluruz.
Not:
![]() açılımındaki her terimdeki çarpanların üsleri toplamı n’e eşittir.
açılımındaki her terimdeki çarpanların üsleri toplamı n’e eşittir.
Alıştırma 2

| | | | | |
Çözüm

Alıştırma 3

| | | | | |
Çözüm

Alıştırma 4

| | | | | |
Çözüm

Not:
![]() açılımındaki ortanca terim
açılımındaki ortanca terim ![]() dir.
dir.
Alıştırma 5

| | | | | |
Çözüm
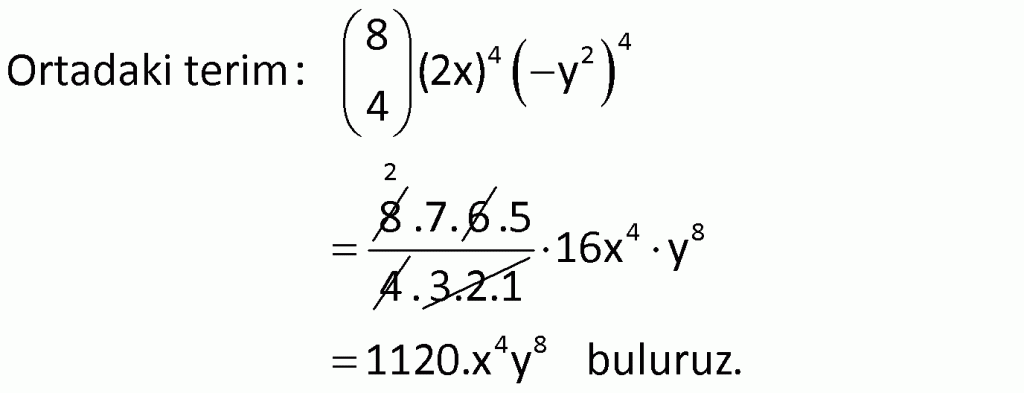
Alıştırma 6

| | | | | |
Çözüm

Alıştırma 7
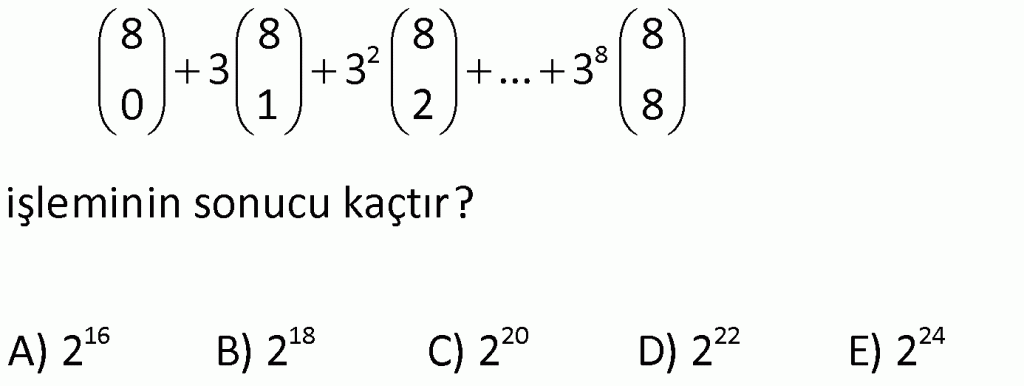
 | | | | |
Çözüm

Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)

