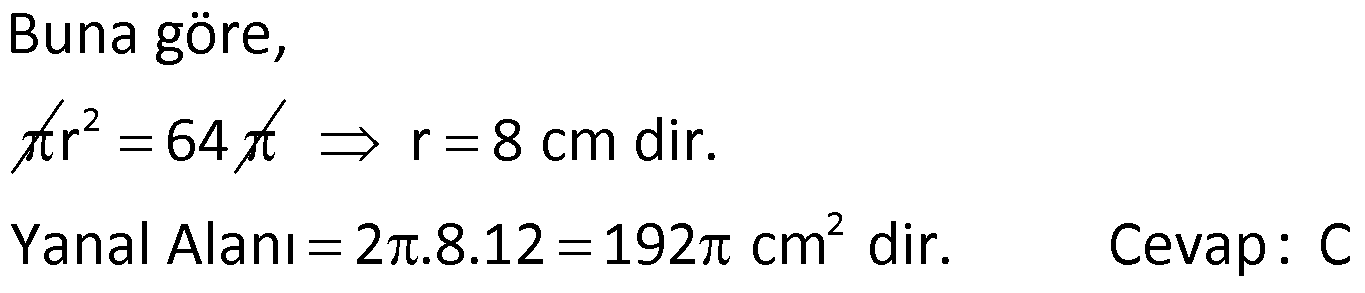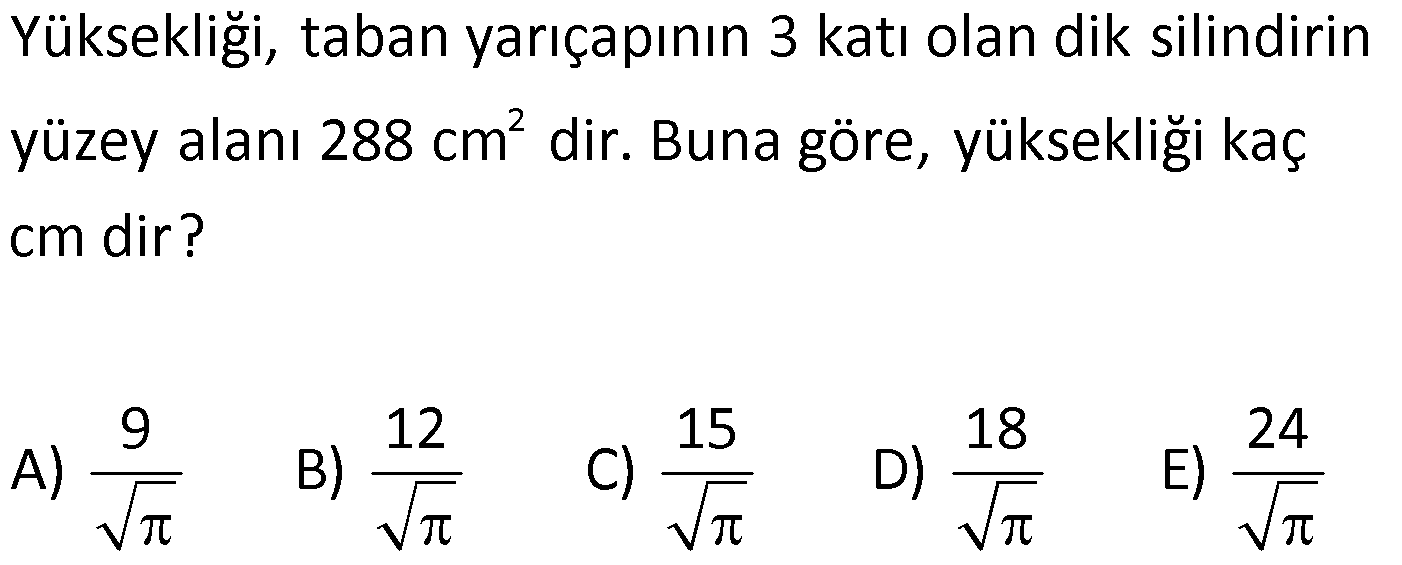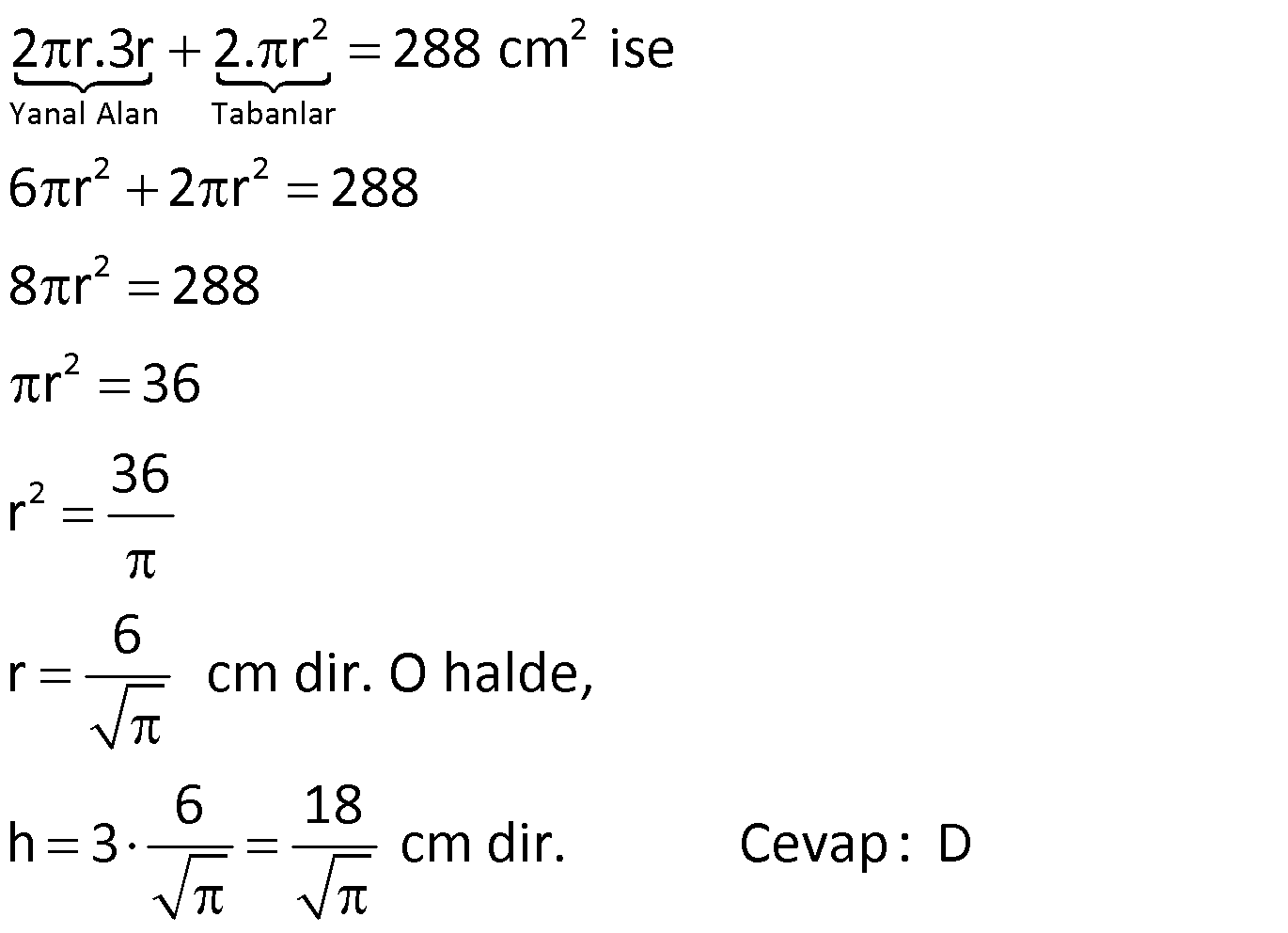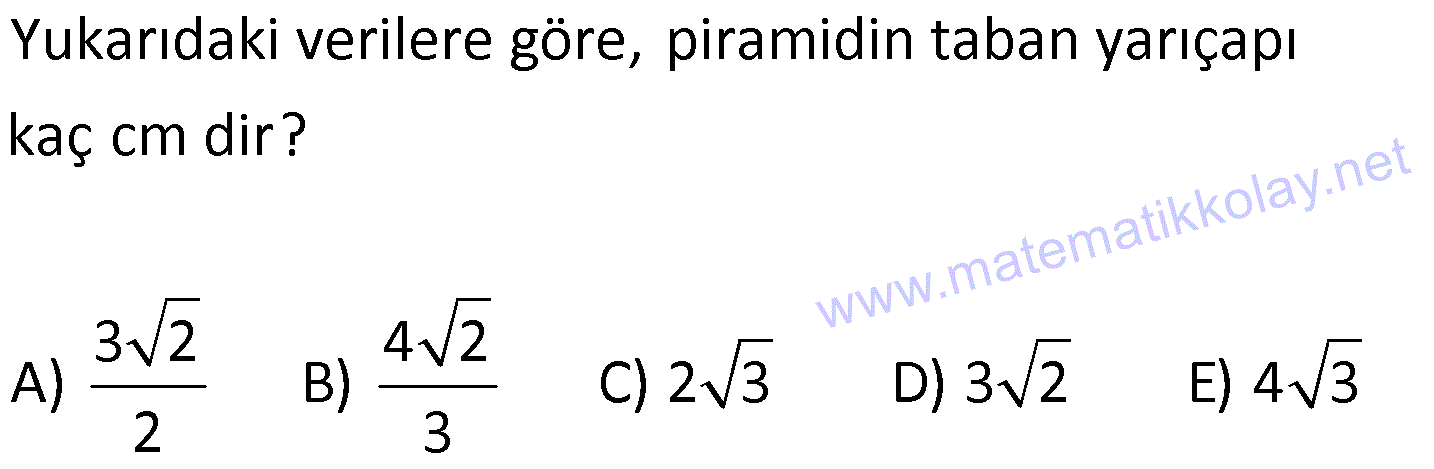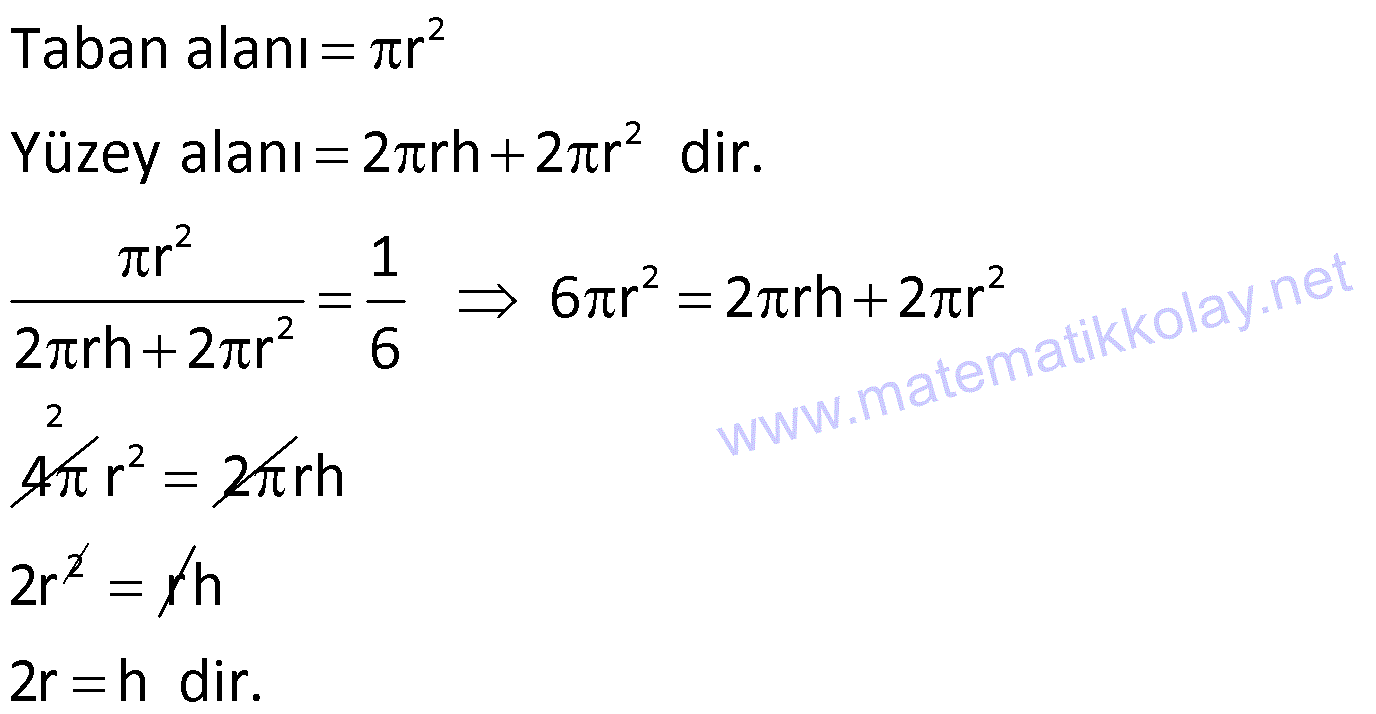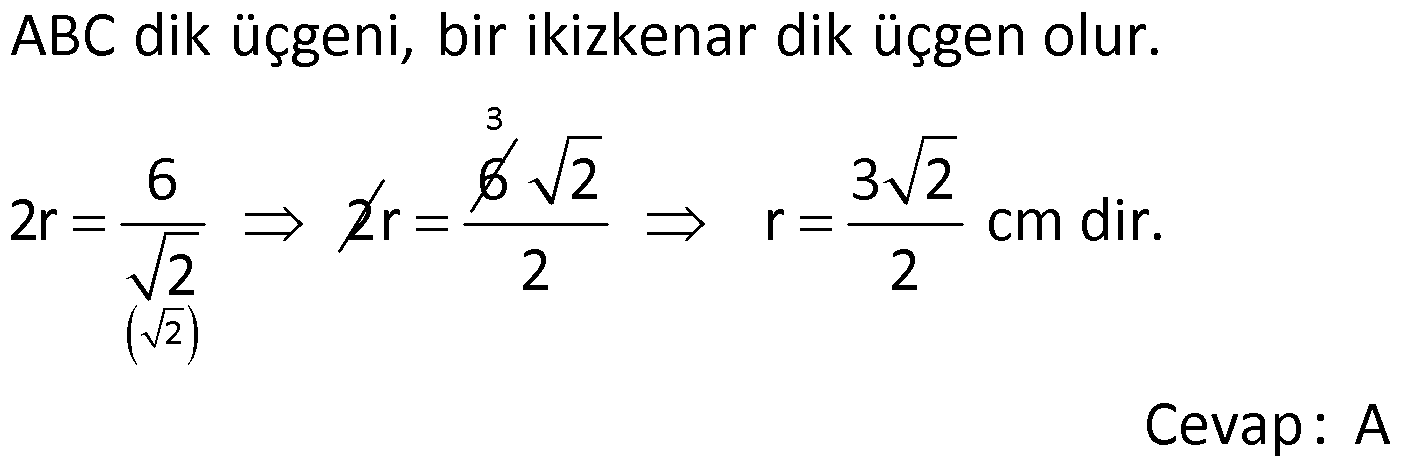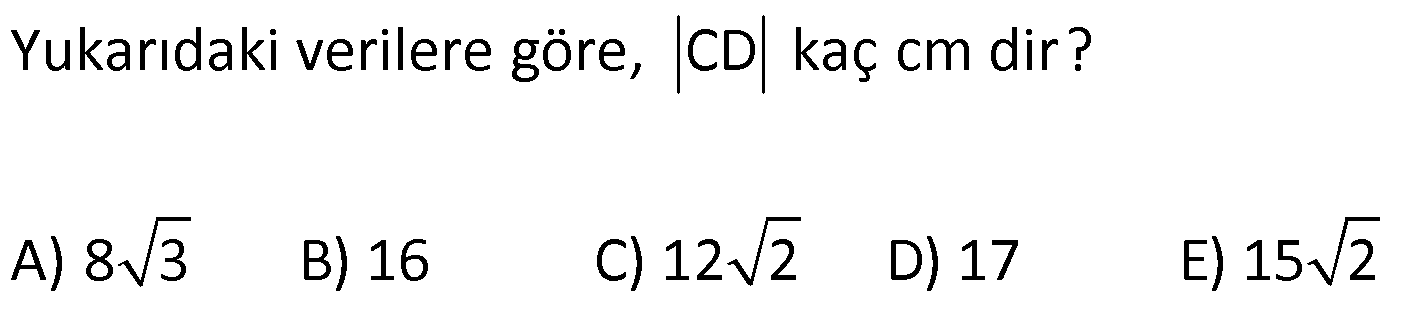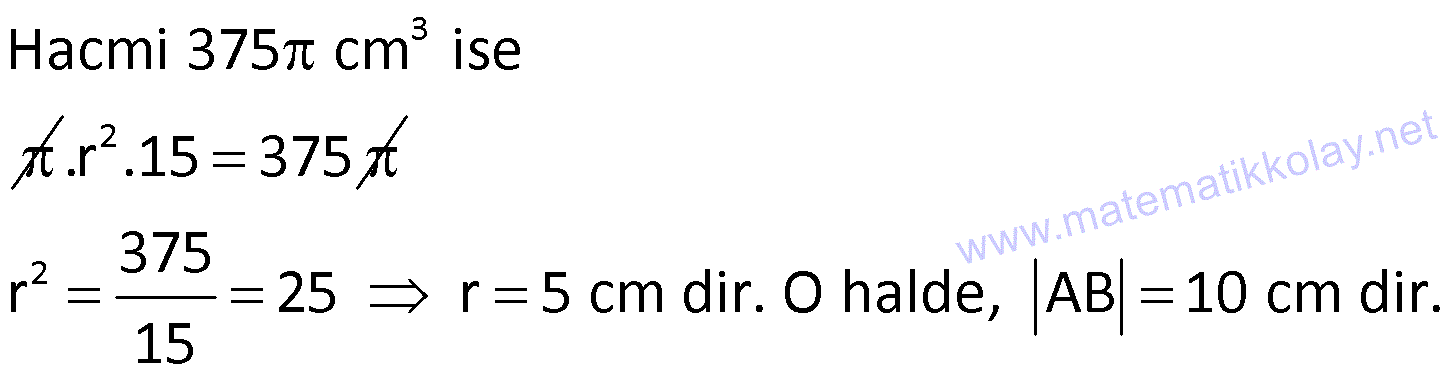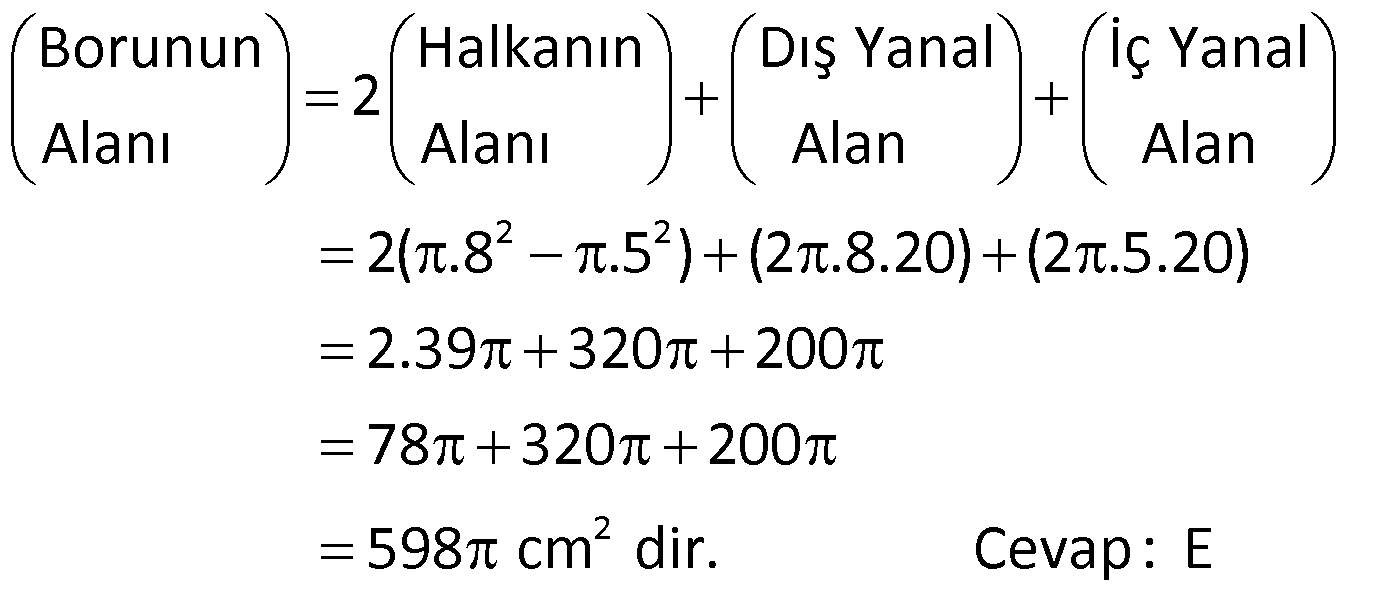Bu bölümde Silindir ile ilgili 21 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
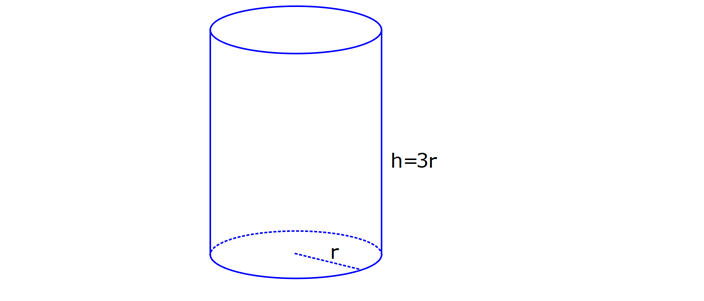
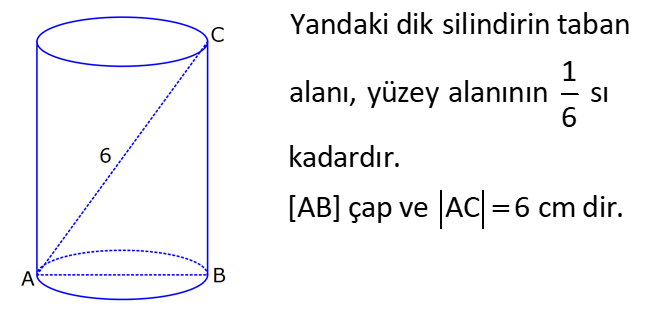
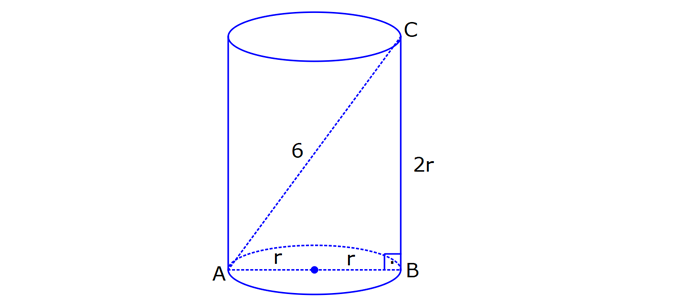
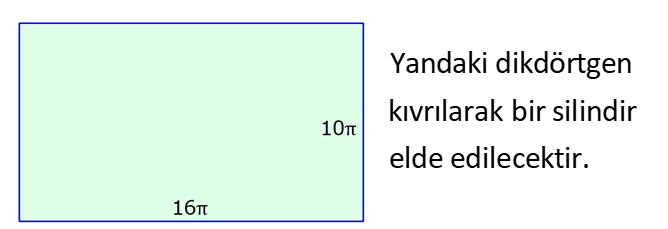
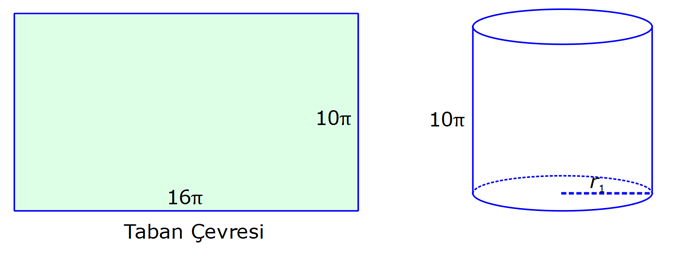
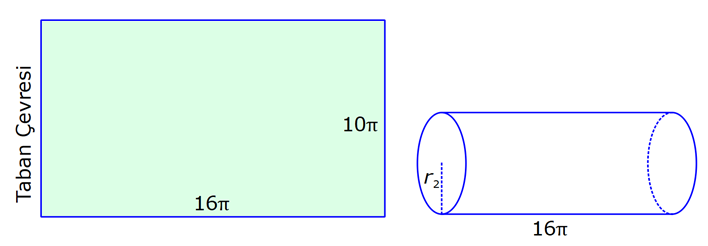
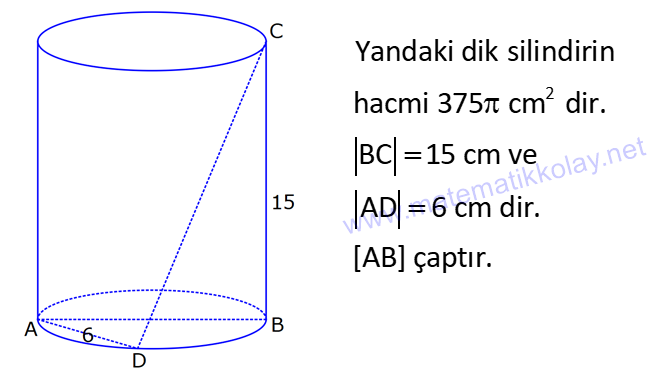
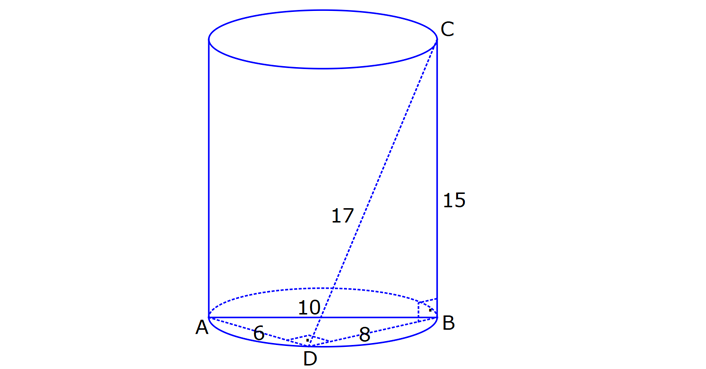
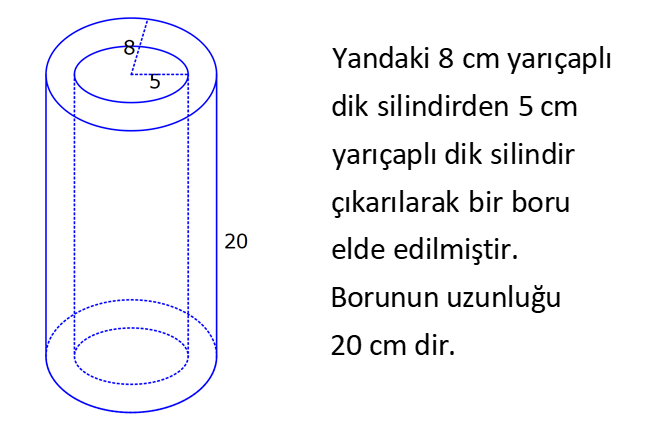
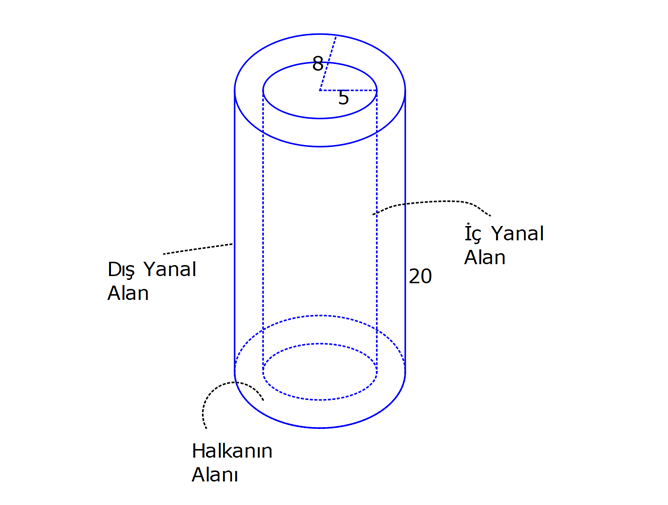
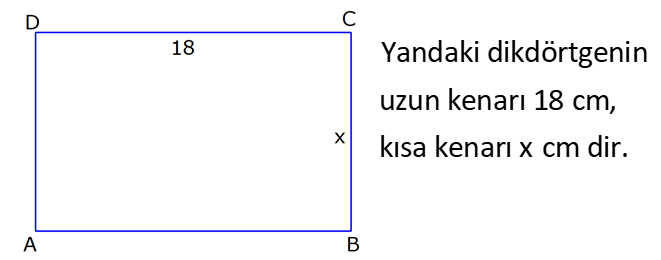
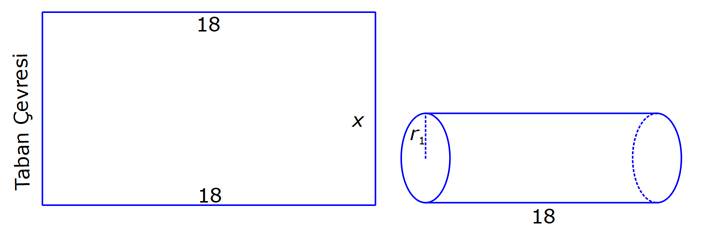
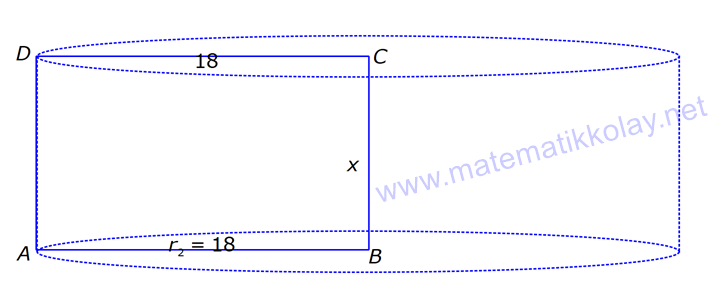
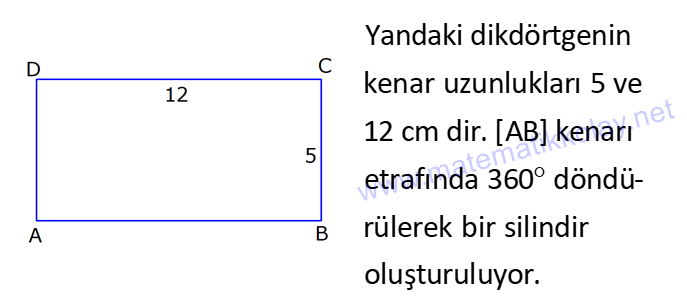
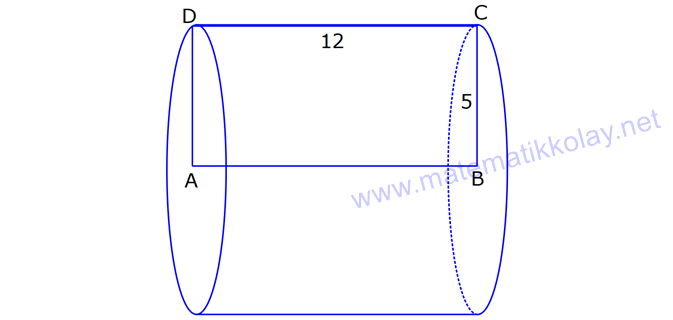
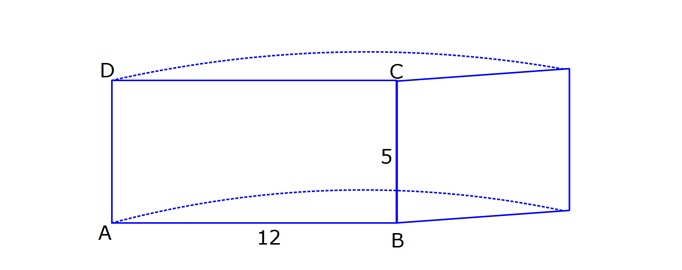
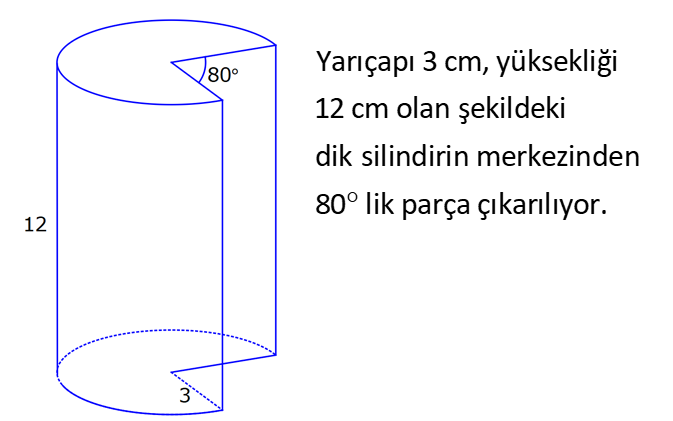
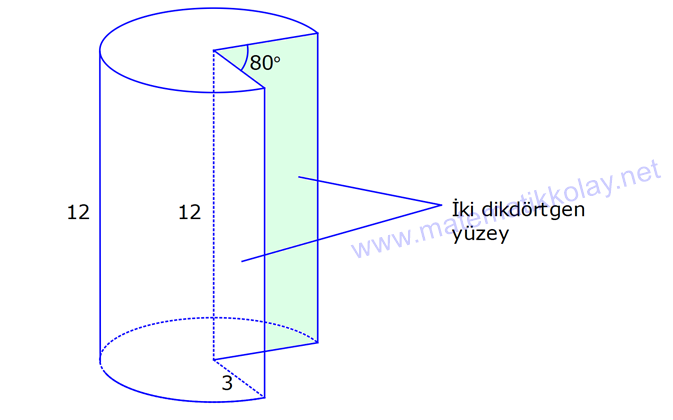
SİLİNDİR www.matematikkolay.net 1) 2 2 Taban alanı 64 cm , yüksekliği 12 cm olan bir dik dairesel silindirin yanal alanı kaç cm dir? A) 144 B) 160 C) 192 D) 216 E) 240 ÇÖZÜM: Taban Çevresi 2 2 Yanal Alt ve Alanı Üst taban Dik dairesel silindirin yarıçapı r, yüksekliği h olmak üzere, Yanal Alanı 2 r .h dir. Taban Alanı r dir. Tüm Alanı 2 rh 2 r dir. Buna göre, 2 r 64 2 r 8 cm dir. Yanal Alanı 2 .8.12 192 cm dir. Cevap : C 2) 2 Yüksekliği, taban yarıçapının 3 katı olan dik silindirin yüzey alanı 288 cm dir. Buna göre, yüksekliği kaç cm dir? 9 12 15 18 24 A) B) C) D) E) ÇÖZÜM: 2 2 Yanal Alan Tabanlar 2 2 2 2 2 2 r.3r 2. r 288 cm ise 6 r 2 r 288 8 r 288 r 36 36 r 6 r cm dir. O halde, 6 18 h 3 cm dir. Cevap : D 3) Yandaki dik silindirin taban 1 alanı, yüzey alanının sı 6 kadardır. [AB] çap ve AC 6 cm dir. Yukarıdaki verilere göre, piramidin taban yarıçapı kaç cm dir? 3 2 4 2 A) B) C) 2 3 D) 3 2 E) 4 3 2 3 ÇÖZÜM: 2 2 2 2 2 2 Taban alanı r Yüzey alanı 2 rh 2 r dir. r 1 6 r 2 rh 2 r 2 rh 2 r 6 4 2 2 r 2 2 rh 2r rh 2r h dir. www.matematikkolay.net 2 ABC dik üçgeni, bir ikizkenar dik üçgen olur. 6 2r 2 2 6 r 3 2 3 2 r cm dir. 2 2 Cevap: A 4) 2 3 1 Çapı, yüksekliğinin ü olan dik silindirin alanı 56 3 cm olduğuna göre bu silindirin hacmi kaç cm tür? A) 40 B) 48 C) 52 D) 60 E) 64 ÇÖZÜM: çap 2 2 2 h 2r ise 6r h dir. 3 Buna göre, 2 r 2 r.6r 56 2 r 12 r 56 14 2 r 56 4 2 2 2 Taban Yük Alanı sek lik 2 3 r 4 r 2 cm dir. h 6r 12 cm dir. Silindirin Hacmi r . h dir. Buna göre, Hacim .2 .12 48 cm tür. Cevap : B Not : 5) Yandaki dikdörtgen kıvrılarak bir silindir elde edilecektir. 1 1 2 2 Kısa kenarları üst üste getirilerek elde edilen silindirin hacmi V , uzun kenarları üst üste getirilerek elde edilen V silindirin hacmi V olduğuna göre, oranı kaçtır? V 3 5 7 8 A) B) C) 1 D) E) 4 6 4 5 ÇÖZÜM: Kısa kenarları üst üste gelirse, taban çevresi 16 olur. 2 1 r 16 1 2 1 Taban Yükseklik Alanı r 8 br olur. V .8 . 10 olur. Uzun kenarları üst üste gelirse, taban çevresi 10 olur. 2 2 r 10 2 2 1 Taban Yükseklik Alanı 1 2 r 5 br olur. V .5 . 16 olur. O halde, V V . 8.8.10. .5. 5. 16 2 . 8 buluruz. Cevap: E 5 www.matematikkolay.net 6) 2 Yandaki dik silindirin hacmi 375 cm dir. BC 15 cm ve AD 6 cm dir. [AB] çaptır. Yukarıdaki verilere göre, CD kaç cm dir? A) 8 3 B) 16 C) 12 2 D) 17 E) 15 2 ÇÖZÜM: 3 Hacmi 375 cm ise 2 .r .15 375 2 375 r 25 r 5 cm dir. O halde, AB 10 cm dir. 15 Çapı gören çevre açı 90 olduğu için ADB üçgeni bir dik üçgendir. 6 – 8 -10 üçgeni olduğu için de, DB 8 cm dir. CBD üçgeni de bir dik üçgendir. 8 -15-17 üçgeni olduğu için de, DC 17 cm dir. Cevap: D 7) Yandaki 8 cm yarıçaplı dik silindirden 5 cm yarıçaplı dik silindir çıkarılarak bir boru elde edilmiştir. Borunun uzunluğu 20 cm dir. 2 3 2 3 2 3 2 3 Yukarıdaki verilere göre, borunun yüzey alanı ve hacmi hangı şıkta doğru gösterilmiştir? A) 398 cm 180 cm B) 398 cm 480 cm C) 520 cm 480 cm D) 520 cm 780 cm E) 59 Alan Hacim 3 3 8 cm 780 cm ÇÖZÜM: 2 2 Hacmini hesaplamak daha kolay. İlk önce hacimle başlayalım. Borunun Büyük Silindirin Küçük Silindirin Hacmi Hacmi Hacmi .8 .20 .5 .20 3 20 64 25 20 .39 780 cm tür. Şimdi yüzey alanına gelelim. www.matematikkolay.net 2 2 Borunun Halkanın Dış Yanal İç Yanal 2 Alanı Alanı Alan Alan 2( .8 .5 ) (2 .8.20) (2 .5.20) 2.39 320 200 78 2 320 200 598 cm dir. Cevap: E 8) Yandaki dikdörtgenin uzun kenarı 18 cm, kısa kenarı x cm dir. 1 2 1 2 Uzun kenarları üst üste gelecek şekilde kıvrılarak elde edilen silindirin hacmi V , [BC] kenarı etrafında 360 döndürülerek oluşturulan silindirin hacmi V olmak V 1 üzere, olduğuna göre, x kaçtır? V 72 9 3 9 2 2 A) B) 2 C) D) E) 2 ÇÖZÜM: 1 1 2 2 2 1 2 Yükseklik Taban Alanı Uzun kenarları üst üste gelirse, taban çevresi x cm olur. x 2 r x r cm olur. 2 x x .18 9x V . . 18 olur. 2 4 2 2 2 Taban Yükseklik Alanı 2 [BC] etrafında 360 döndürülünce, 18 cm yarıçaplı bir silindir elde edilir. V .18 . x 324 x olur. Buna göre, 9x 1 2 ise, 324 x 72 9 2 x 1 2 324 36 2 1 x 72 x 72 2 1 x 72 2 2 2 x x x dir. Cevap : C 9) Yandaki dikdörtgenin kenar uzunlukları 5 ve 12 cm dir. [AB] kenarı etrafında 360 döndü- rülerek bir silindir oluşturuluyor. Eğer [BC] kenarı etrafında döndürseydik, aynı hacimli bir cisim oluşturmak için kaç derece döndürmemiz gerekirdi? A) 120 B) 150 C) 180 D) 210 E) 240 ÇÖZÜM: 2 2 Taban Yükseklik Alanı [AB] etrafında 360 döndürülünce, 5 cm yarıçaplı bir silindir elde edilir. V .5 . 12 300 olur. www.matematikkolay.net [BC] etrafında döndürülünce, 12 cm yarıçaplı bir silindirin ı kadar bir cism elde edilir. 360 Eşit hacimli olması için 2 Yükseklik Taban Alanı .12 . 5 . 300 360 olmalıdır. 12.12.5. 360 30 300 5 5.30 150 buluruz. Cevap : B 10) Yarıçapı 3 cm, yüksekliği 12 cm olan şekildeki dik silindirin merkezinden 80 lik parça ç ıkarılıyor. 2 Buna göre, kalan kısmın yüzey alanı kaç cm dir? A) 56 36 B) 64 72 C) 70 72 D) 72 36 E) 80 48 ÇÖZÜM: 2 Başlangıçta yanal alan 2 .3.12 72 cm dir. 80 lik kısım çıkınca geriye 280 lik kısım kalır. Bu da, 72 8 280 7 360 9 2 2 2 56 cm yapar. Başlangıçta taban alanı .3 9 cm dir. 280 lik kısmı 9 280 7 360 9 2 2 Alt ve İki dikdörtgen Üst Taban 7 cm dir. Ayrıca iki tane dikdörtgen yüzey oluşur. Birisinin alanı 3.12 36 cm dir. Buna göre; Yeni cismin yüzey alanı 56 2.7 2.36 56 14 72 2 70 72 cm buluruz. Cevap : C
