Oran

Örnek:
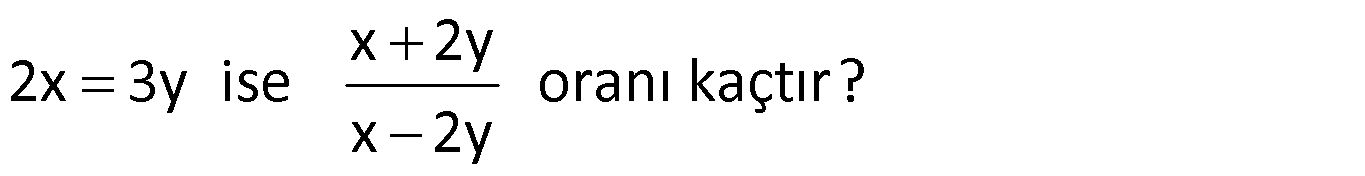
Çözüm:

Orantı

Örnek:

Çözüm:
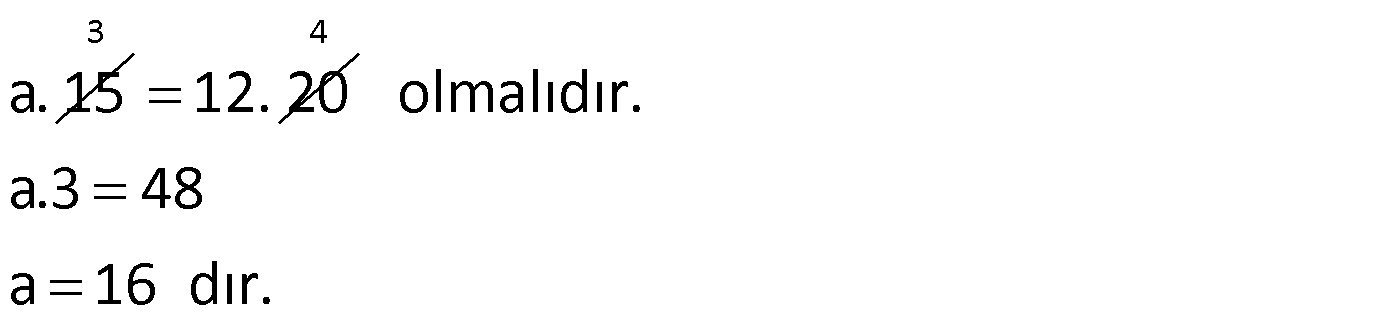
Örnek:
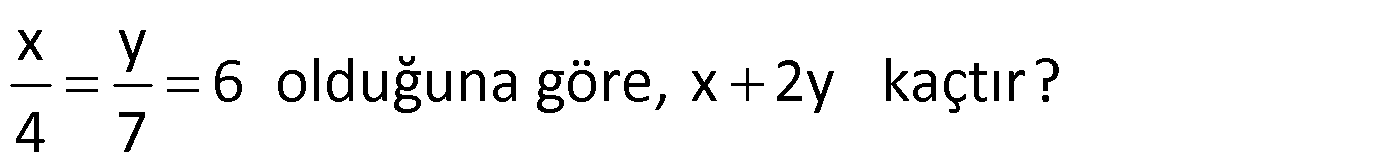
Çözüm:

Örnek:
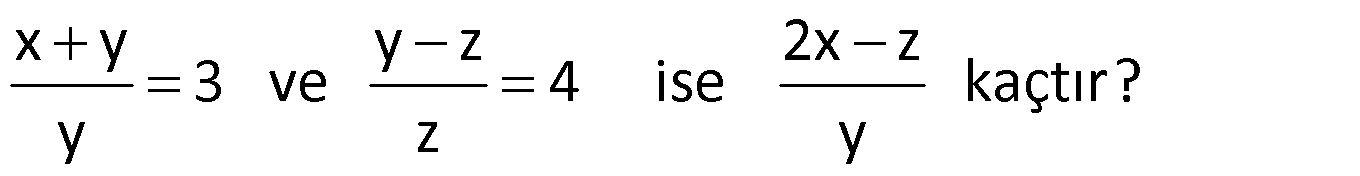
Çözüm:
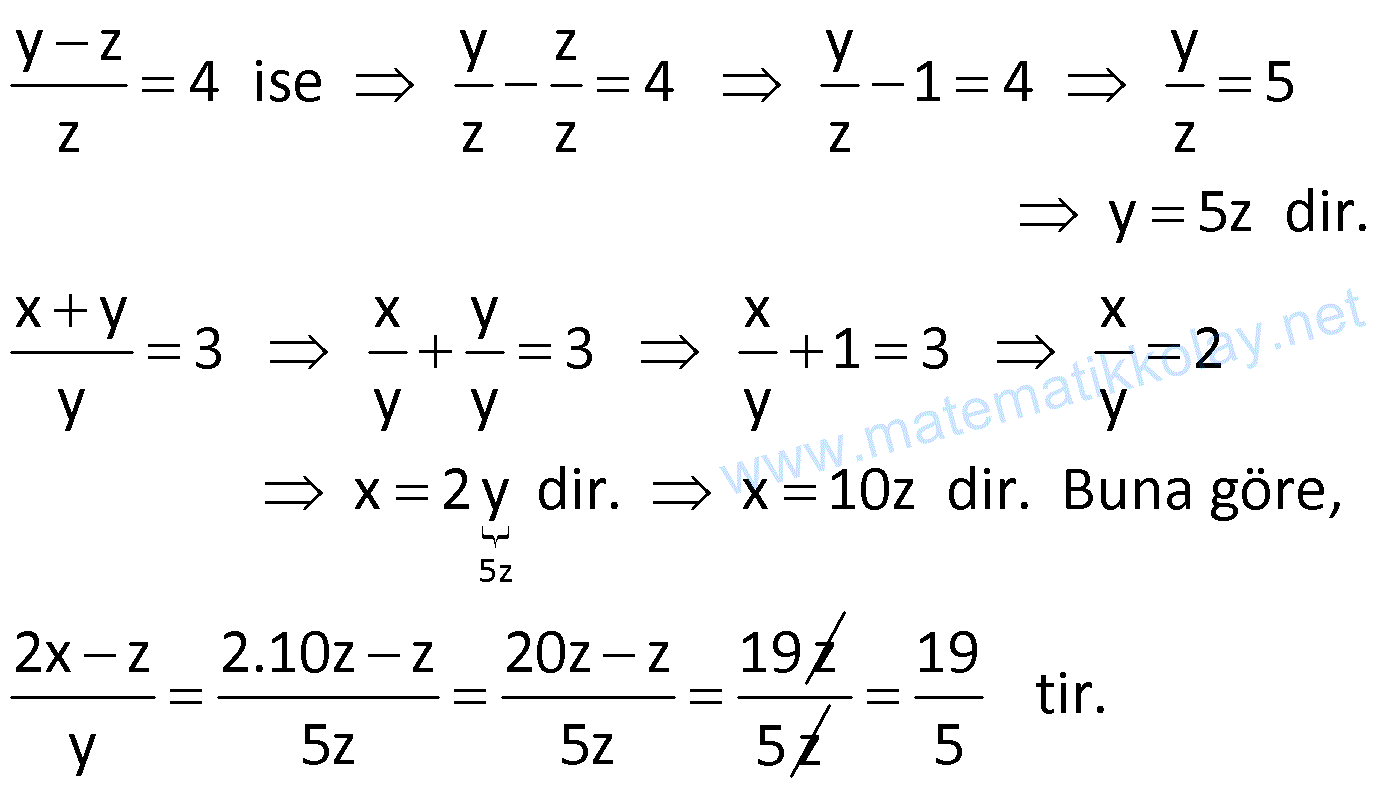
Örnek:

Çözüm:

Üçlü Orantı
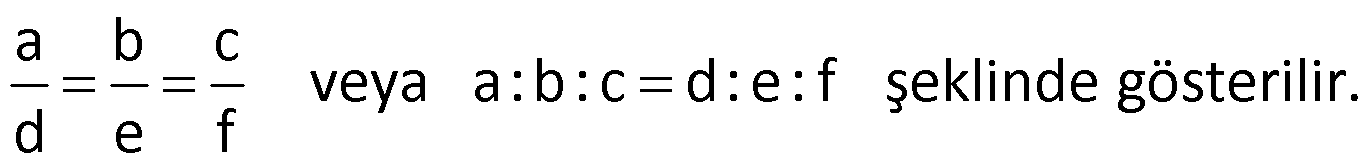
Örnek:
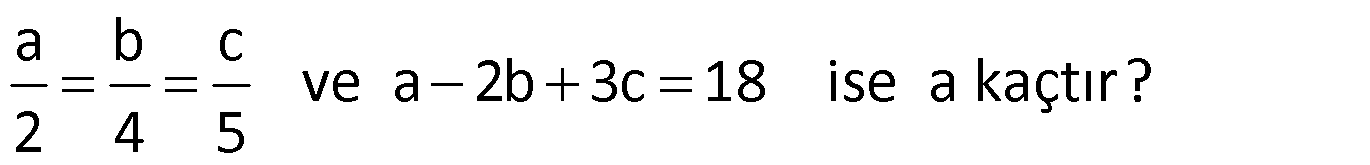
Çözüm:

Örnek:
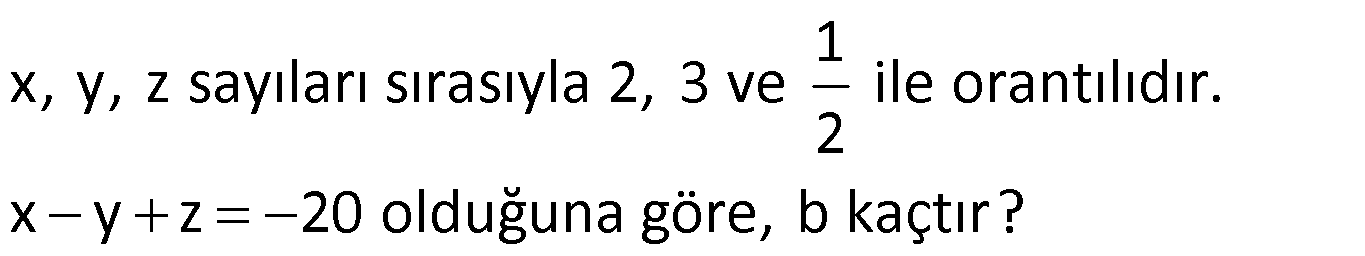
Çözüm:

Not: Bir orantıda payları kendi arasında, paydaları da kendi arasında toplarsak orantı sabiti değişmez.
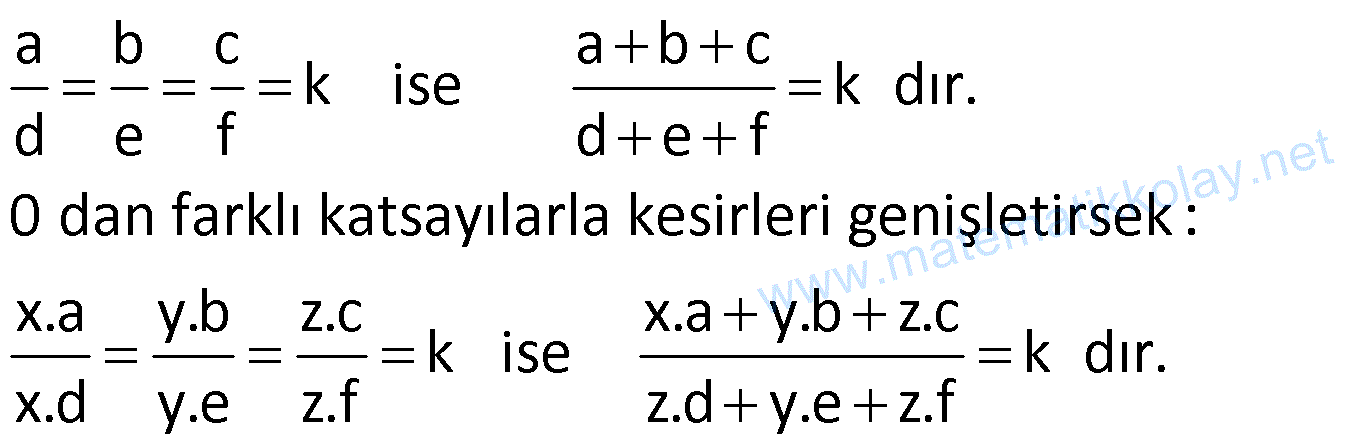
Örnek:

Çözüm:

Not: Orantıdaki kesirlerin kaçıncı kuvvetini aldıysak, orantı sabitinin de o kuvvetini almalıyız.
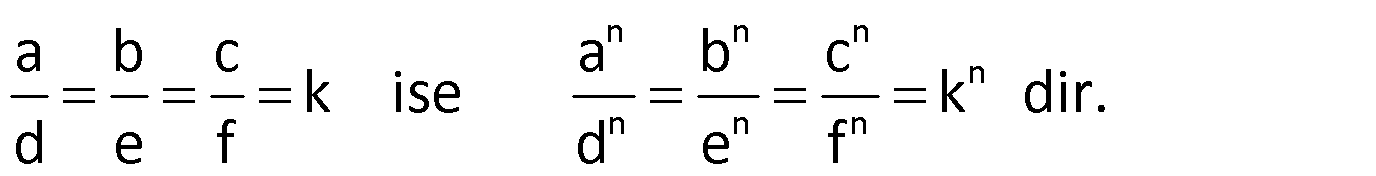
Örnek:
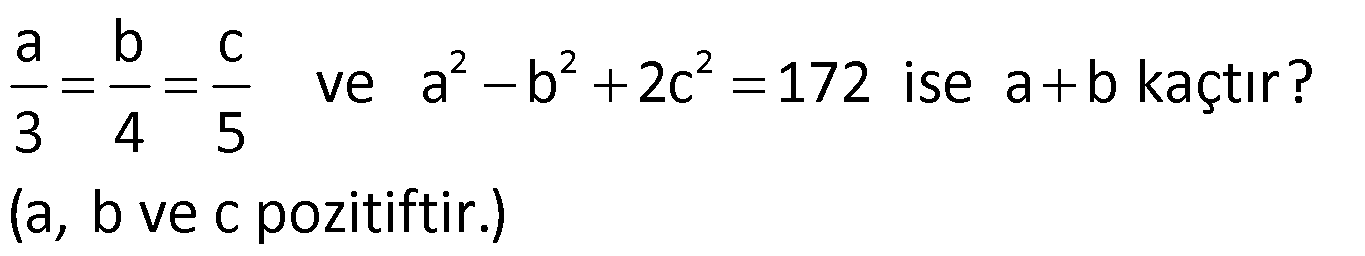
Çözüm:
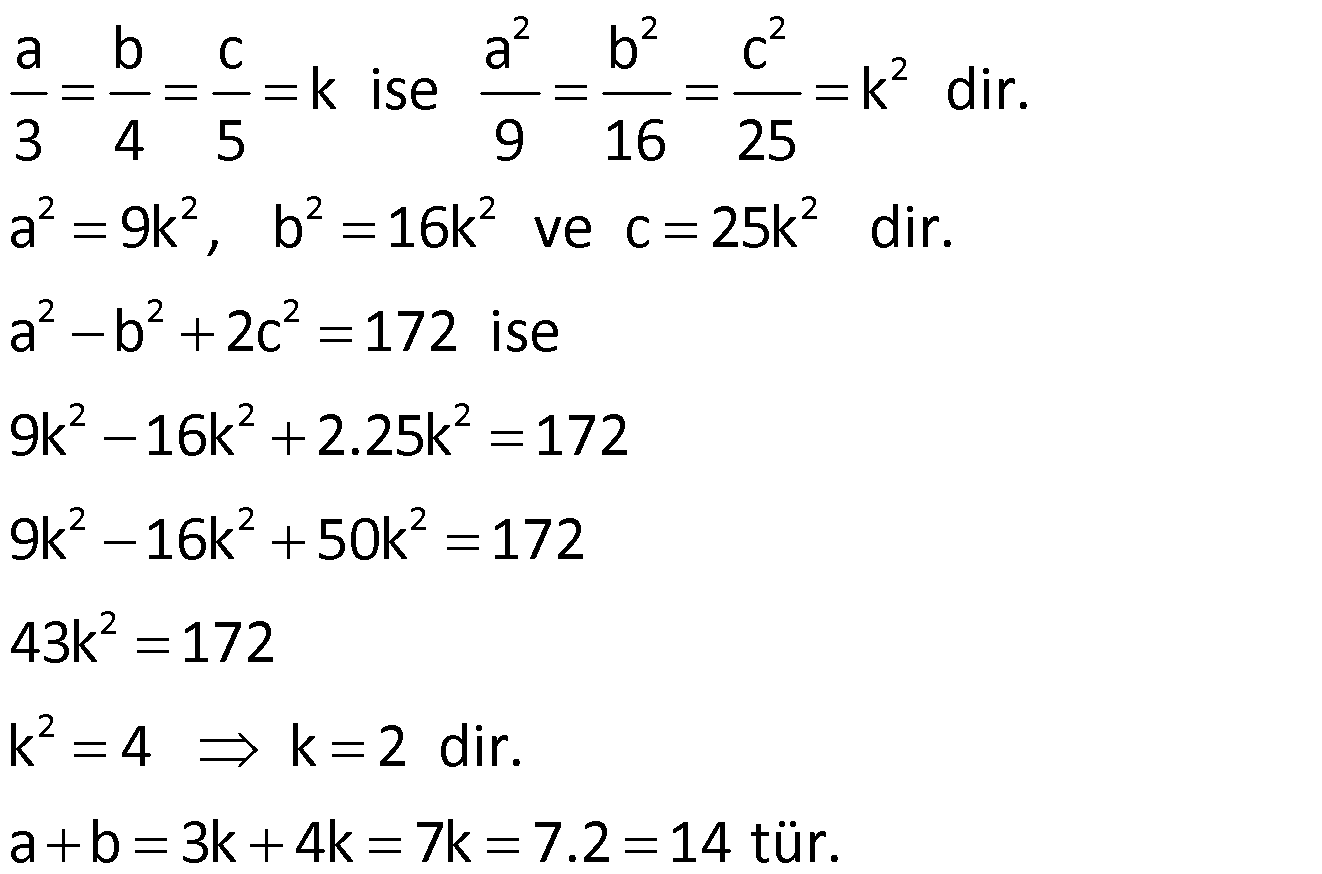
Orantı Çeşitleri
Doğru Orantı
İki çokluktan biri artarken diğeri de artıyorsa veya biri azalırken diğeri de azalıyorsa doğru orantı vardır.
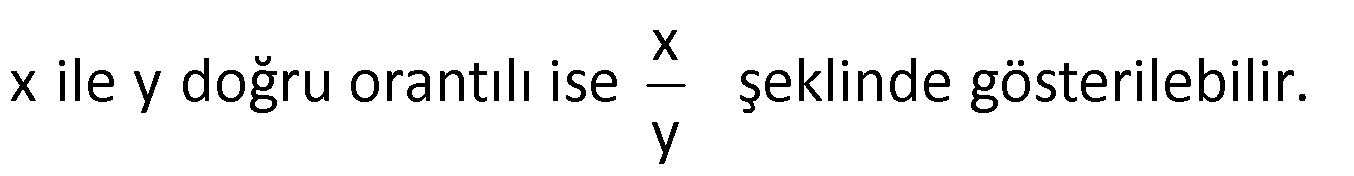
Doğru orantı grafikleri ise aşağıdaki gibidir:
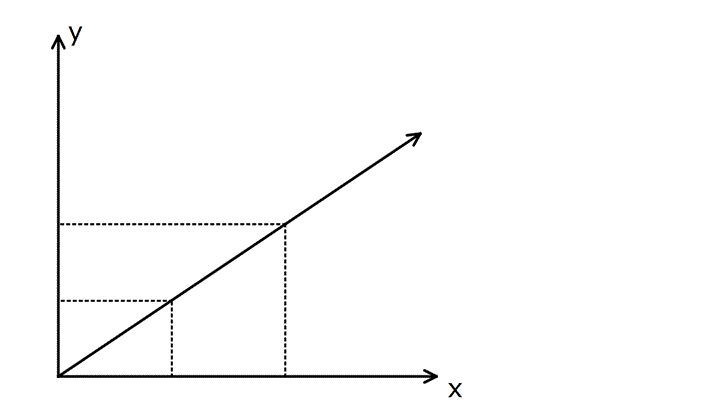
Örnek:

Çözüm:
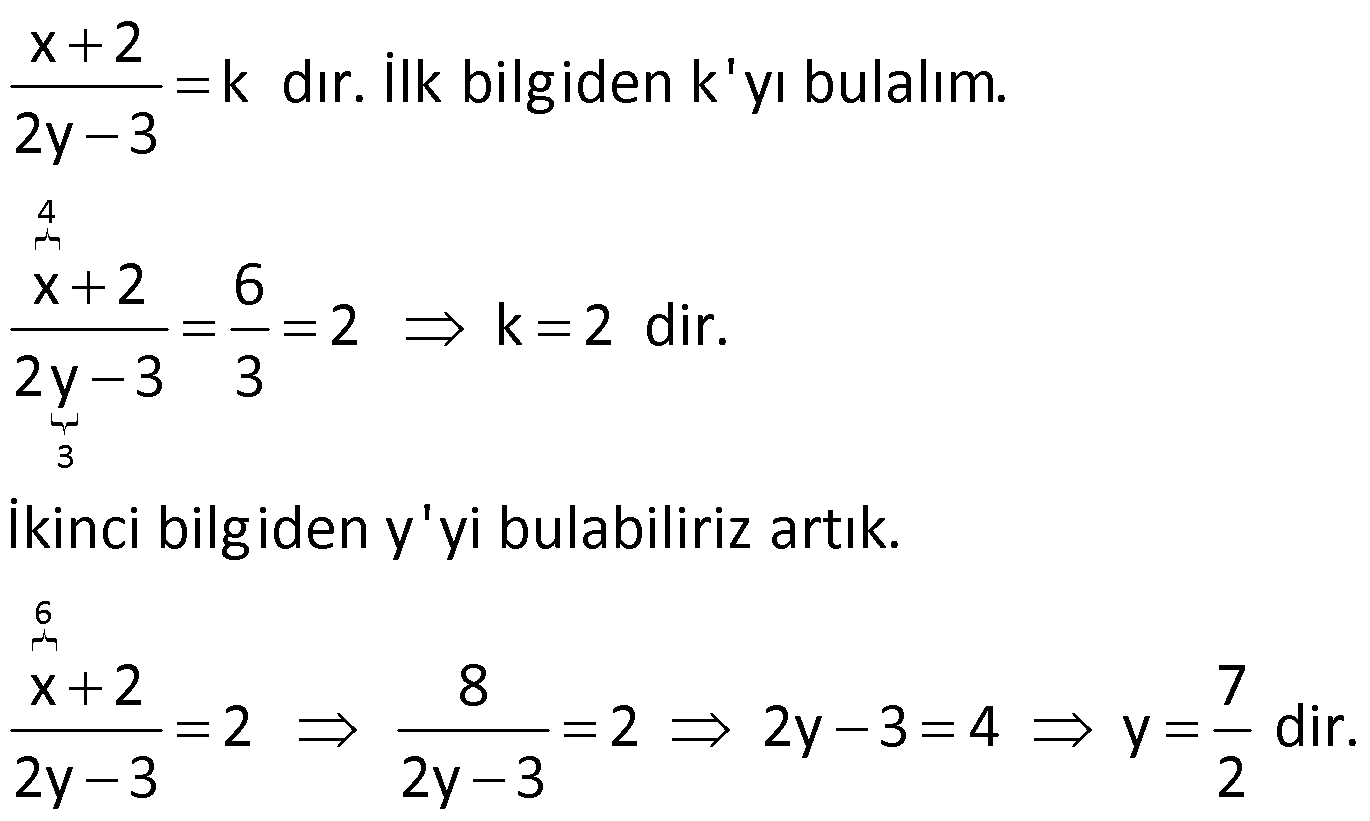
Not: a ile b ve c ile d doğru orantılı ise,
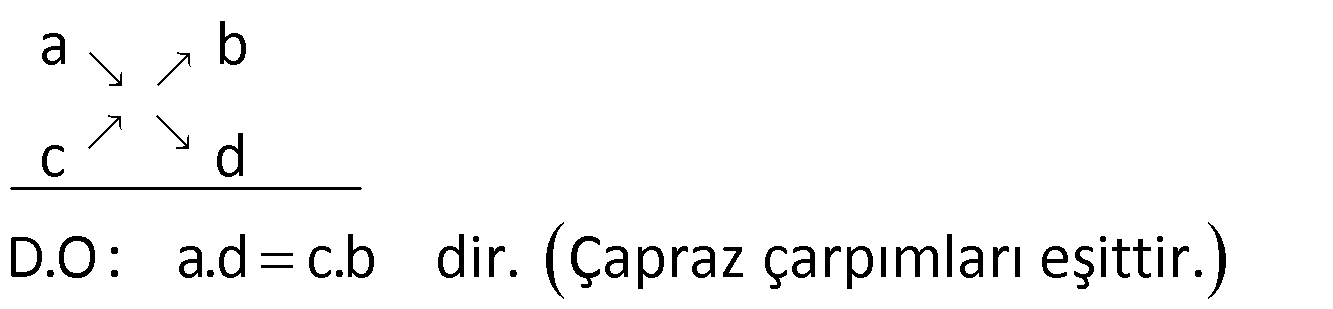
Örnek:
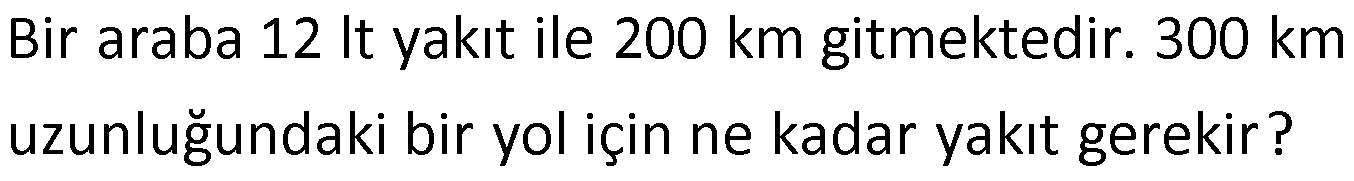
Çözüm:
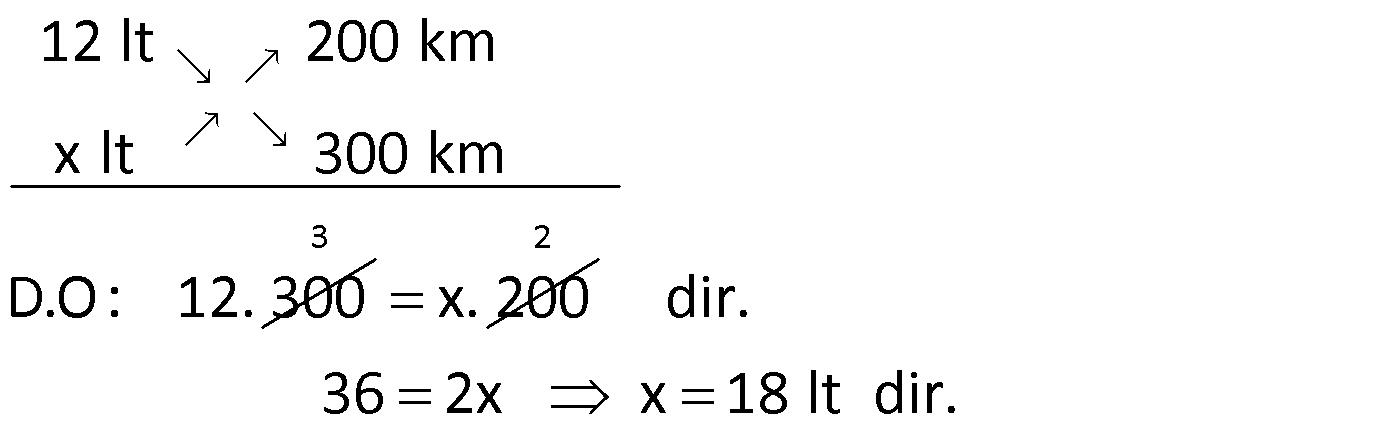
Not: Sadece “orantılıdır” diye belirtiliyorsa bundan doğru orantıyı anlayacağız.
Örnek:
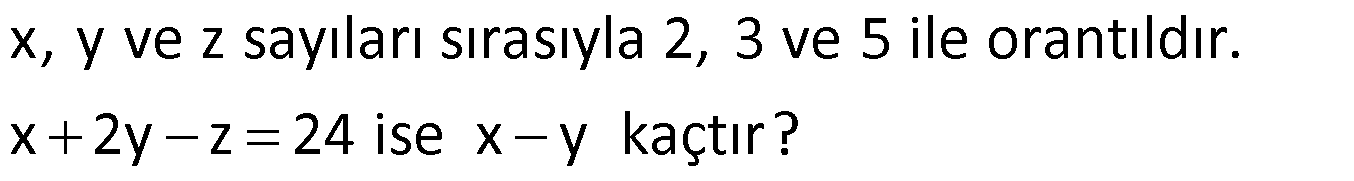
Çözüm:
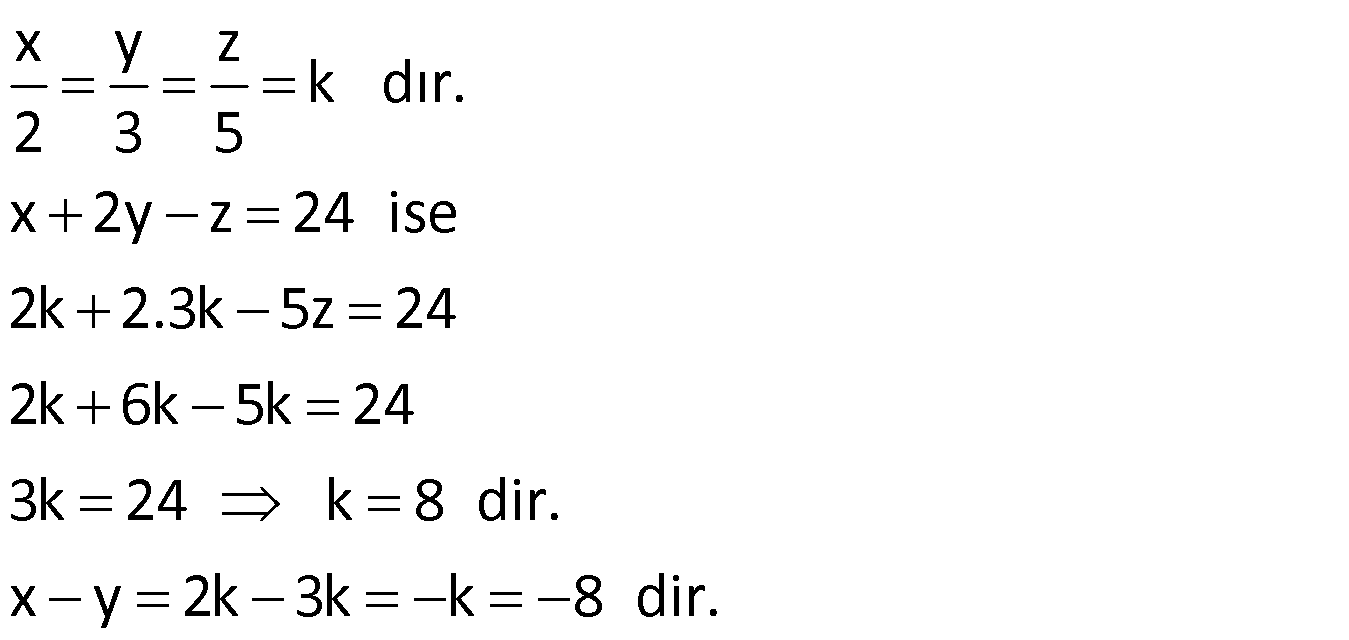
Örnek:

Çözüm:

Ters Orantı
İki çokluktan biri artarken diğeri azalıyorsa veya biri azalırken diğeri artıyorsa burada ters orantı vardır.
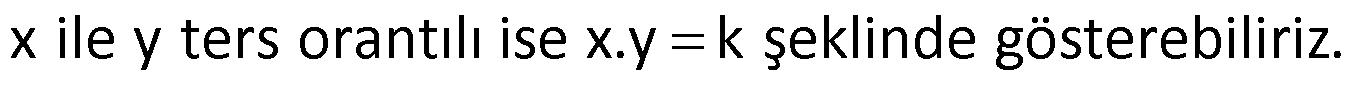
Ters orantı grafikleri ise aşağıdaki gibidir:
Örnek:

Çözüm:

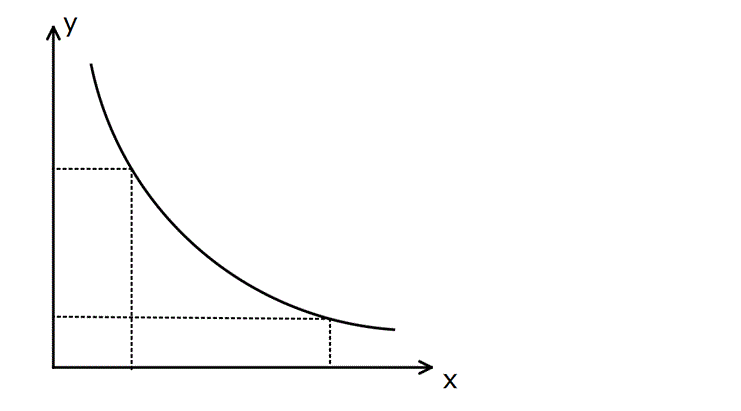
Not: a ile b ve c ile d ters orantılı ise,
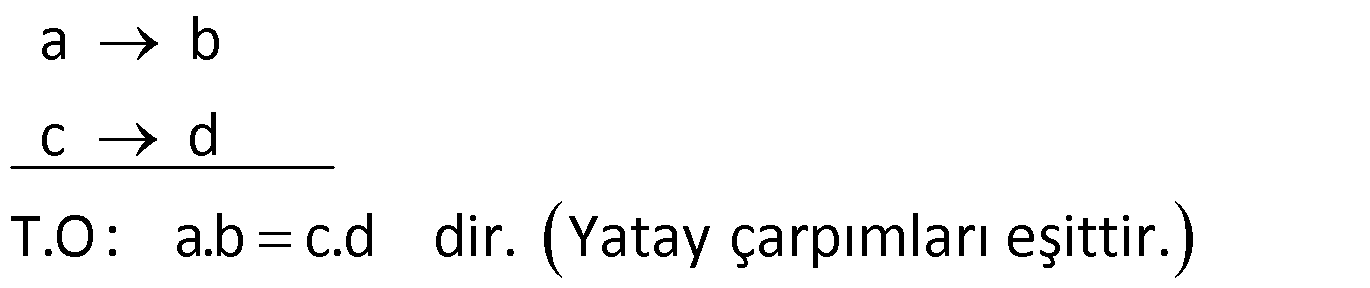
Örnek:
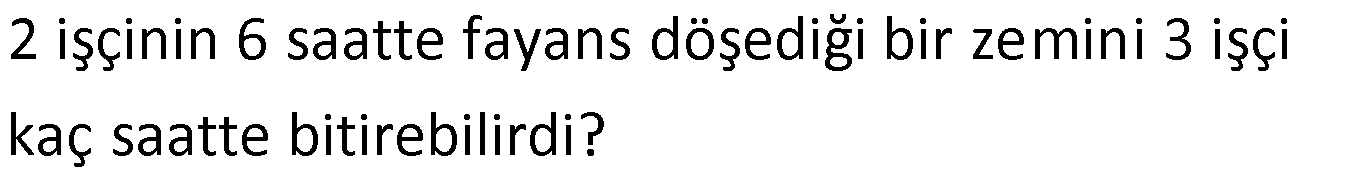
Çözüm:
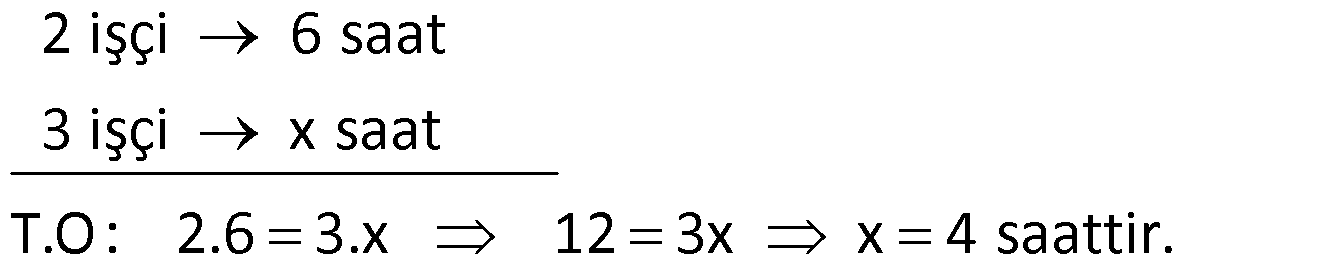
Örnek:
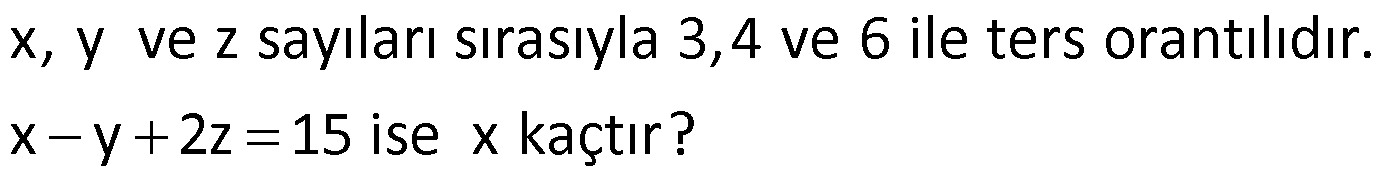
Çözüm:

Örnek:

Çözüm:

Birleşik Orantı
Birden fazla orantı varsa, bu bir birleşik orantıdır.

Örnek:

Çözüm:

Örnek:

Çözüm:
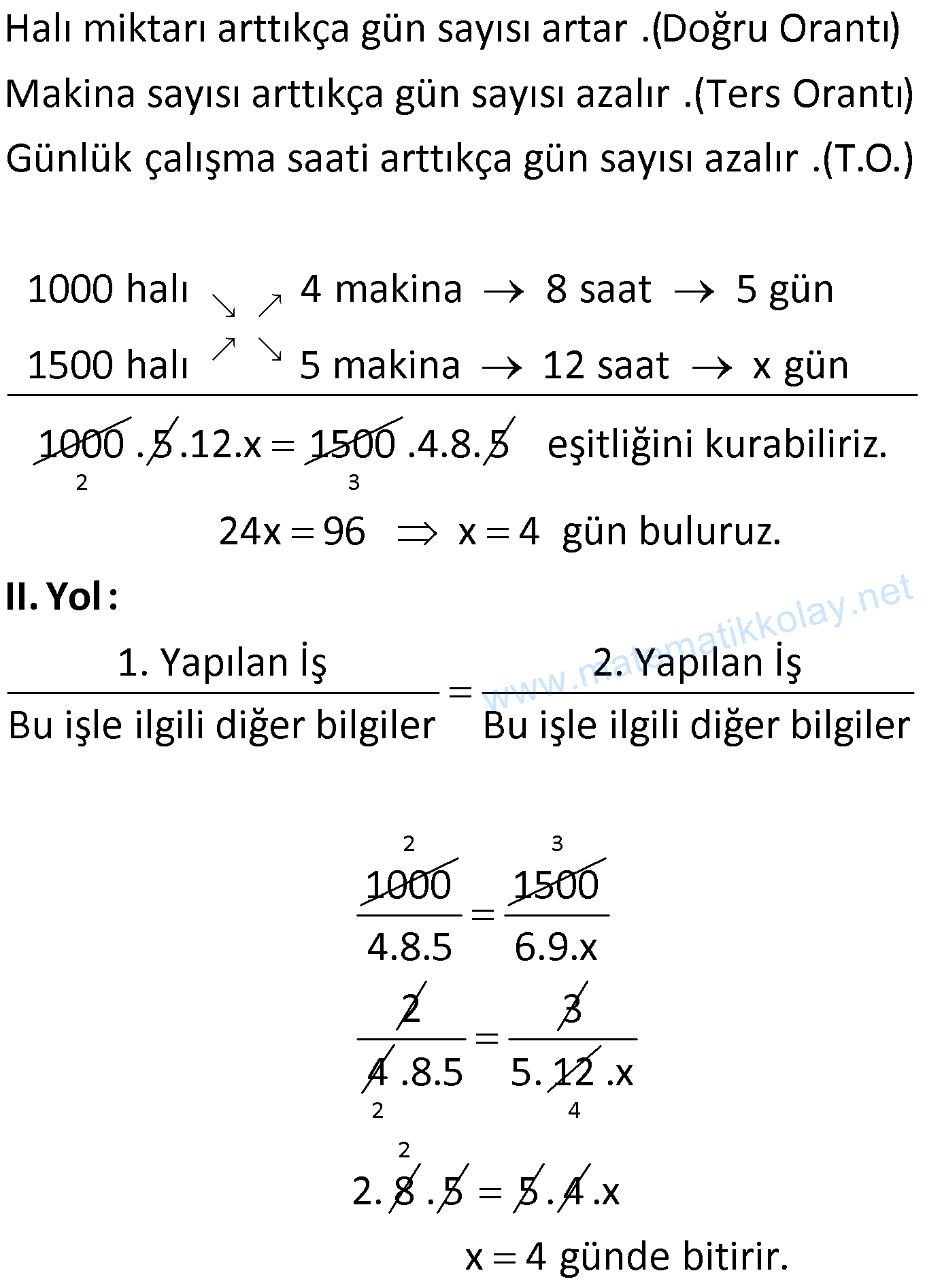
Örnek:

Çözüm:

Aritmetik Ortalama
n tane sayının toplamını n’ye bölersek aritmetik ortalamayı buluruz.
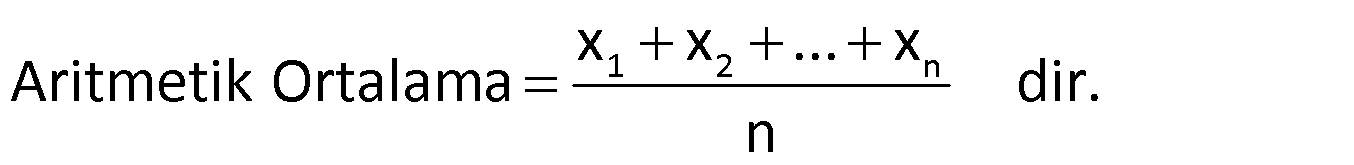
Örnek:
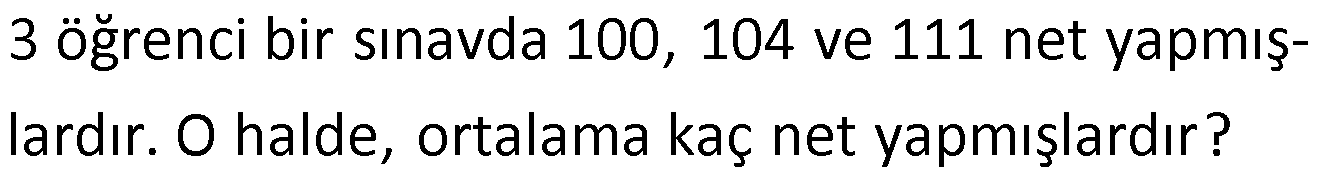
Çözüm:
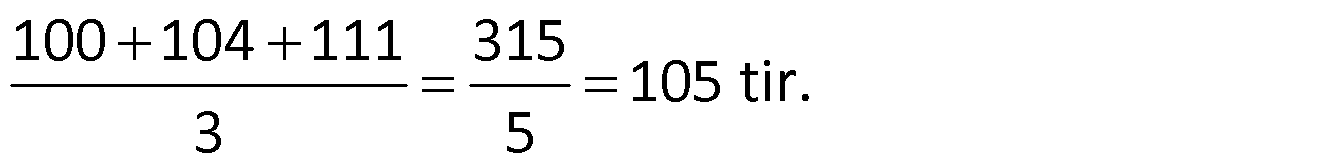
Not: n tane sayının aritmetik ortalaması x ise, bu sayıların toplamı n.x tir.
Örnek:

Çözüm:

Not: n tane sayının aritmetik ortalaması x ise, bu sayıların her biri A ile çarpılıp, her birine B eklenirse yeni ortalama Ax+B olur.
Örnek:

Çözüm:
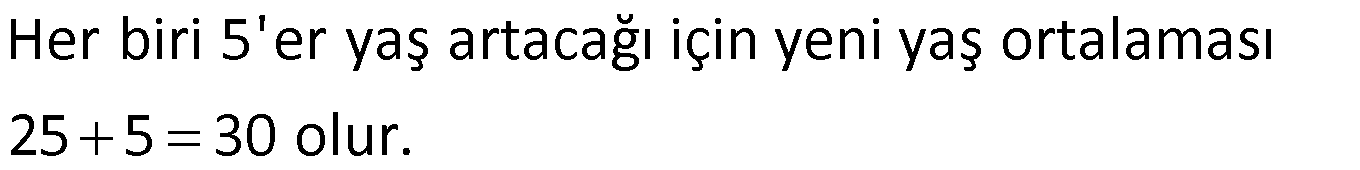
Geometrik Ortalama
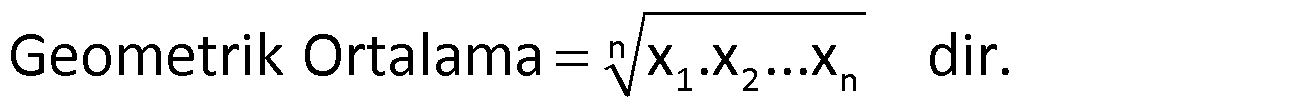
Örnek:

Çözüm:
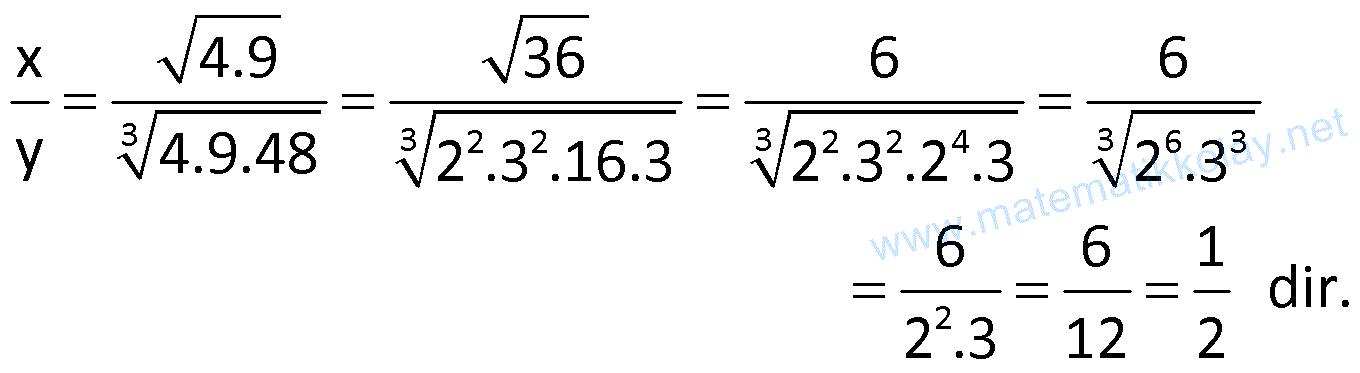
Not: Aritmetik ortalaması ile geometrik ortalaması eşit olan iki sayı birbirine eşittir.
Örnek:

Çözüm:

Orta Orantılı
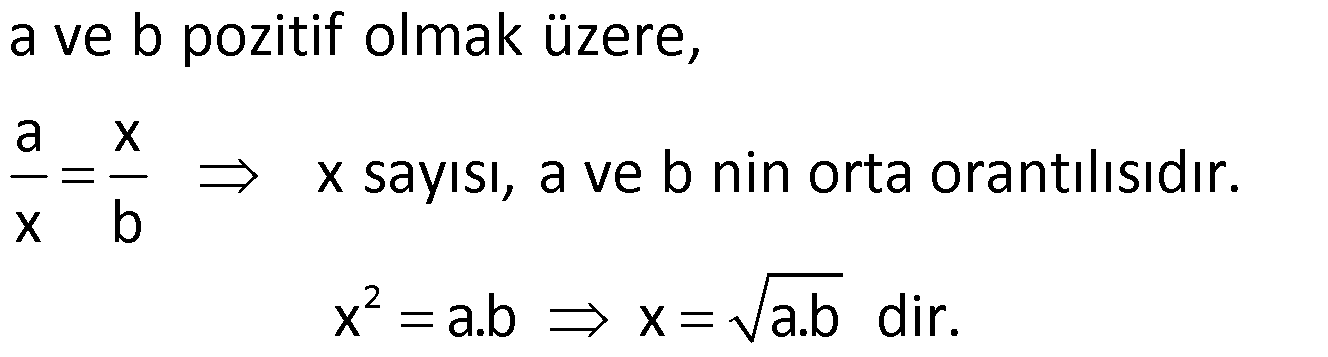
Örnek:
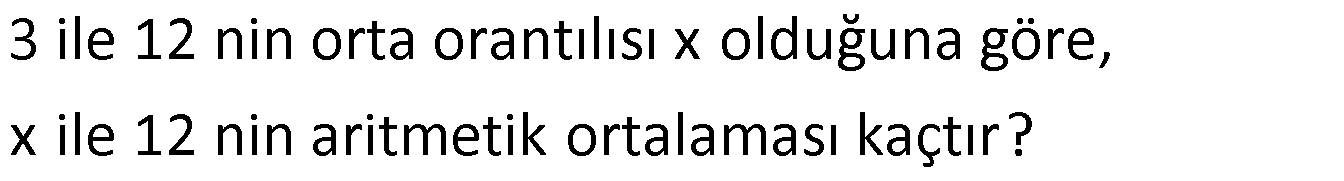
Çözüm:

Çözümlü Soruları ve Çıkmış Soruları Görmek için Tıkla
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)ORAN ORANTI KONU ANLATIMI www.matematikkolay.net Oran a b 0 olmak üzere, ifadesine a’nın b’ye oranı denir. b a ve b aynı birimde olmalıdır. 3 elmanın 4 portakala oranı olmaz. Oran, birimsizdir. 3 3 elmanın 4 elmaya oranı tür. 4 a ifadesi a:b ol b arak da gösterilebilir. Örnek: x 2y 2x 3y ise oranı kaçtır? x 2y Çözüm: 3k x 3k olsun. 2 x 3y 6k 3y y 2k olur. Sorulan ifadede bunları kullanırsak, x 2y 3k 4k 7k x 2y 3k 4k k 7 buluruz. Orantı Dışlar İçler İki veya daha fazla oranın eşitliğine orantı denir. a c k a:b c : d k gibi. b d k Orantı sabitidir. İçler çarpımı dışlar a:b c : d b.c a.d çarpımına eşittir. Örnek: a 12 ise a kaçtır? 20 15 Çözüm: a. 15 3 Ara.20 4 olmalıdır. a.3 48 a 16 dır. Örnek: x y 6 olduğuna göre, x 2y kaçtır? 4 7 Çözüm: x 6 ise x 24 tür. 4 y 6 ise y 42 dir. 7 x 2y 24 42 66 dır. Örnek: x y y z 2x z 3 ve 4 ise kaçtır? y z y Çözüm: 5z y z y z y y 4 ise 4 1 4 5 z z z z z y 5z dir. x y x y x x 3 3 1 3 2 y y y y y x 2 y dir. x 10z di r. Buna göre, 2x z 2.10z z 20z z 19 z y 5z 5z 5z 19 tir. 5 Örnek: Bir okuldaki kız öğrencilerin sayısının erkek öğrenci – 8 lerin sayısına oranı , öğretmenlerin sayısının kız 9 1 öğrencilerin sayısına oranı dır. Bu okulda toplam 6 510 öğrenci olduğuna göre, kaç öğretmen vardır ? Çözüm: www.matematikkolay.net Öğretmenlerin sayısına k diyelim. Kız öğrencilerin sayısı 6k olur. Kız Öğrenciler 8 6k ise Erkek Öğrenciler 9 3k 8 Erkek Öğrenciler 4 9 4. Erkek Öğrenciler 27k 27k Erkek Öğrenciler= olur. 4 510 öğrenci varsa, 27k 6k 510 4 27k 24k 510 4 51 k 510 4 10 k 40 tır. Öğretmen Sayısı Üçlü Orantı a b c veya a:b: c d: e: f şeklinde gösterilir. d e f Örnek: a b c ve a 2b 3c 18 ise a kaçtır? 2 4 5 Çözüm: a b c k olsun. 2 4 5 a 2k, b 4k ve c 5k olur. a 2b 3c 18 ise 2k 2.4k 3.5k 18 2k 8k 15k 18 9k 18 k 2 dir. a 2k 2.2 4 tür. Örnek: 1 x, y, z sayıları sırasıyla 2, 3 ve ile orantılıdır. 2 x y z 20 olduğuna göre, b kaçtır? Çözüm: x y z dir. Bu orantının sabiti k olsun. 2 3 1 2 k x 2k, y 3k, z dir. 2 x y z 20 ise k 2k 3k 20 2 k 20 k 40 tır. 2 y 3k 3.40 120 dir. Not: Bir orantıda payları kendi arasında, paydaları da kendi arasında toplarsak orantı sabiti değişmez. a b c a b c k ise k dır. d e f d e f 0 dan farklı katsayılarla kesirleri genişletirsek : x.a y.b z.c x.a y.b z.c k ise k dır. x.d y.e z.f z.d y.e z.f Örnek: a b c 2 d e f 3 2a b 3c 16 e 3f 6 ise ise a kaçtır? Çözüm: olur. Pay ve paydayı kendi arasında toplarsak olur. 2a-b 3c 16 bilgisini kullanalım. olur. e Orantıdaki kesirleri uygun katsayılarla genişletelim. 2a b 3c 2 2d e 3f 3 2a b 3c 2 2d e 3f 3 16 2 2d e 3f 3 3f 6 bilgisini kullanalım. 16 8 2 2d 6 15 3 2d 6 24 2d 30 d 15 tir. Başlangıçtaki orantıyı kullanırsak, a 2 3a 30 a 10 dur. d 3 Not: Orantıdaki kesirlerin kaçıncı kuvvetini aldıysak, orantı sabitinin de o kuvvetini almalıyız. www.matematikkolay.net n n n n n n n a b c a b c k ise k dir. d e f d e f Örnek: 2 2 2 a b c ve a b 2c 172 ise a b kaçtır? 3 4 5 (a, b ve c pozitiftir.) Çözüm: 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 a b c a b c k ise k dir. 3 4 5 9 16 25 a 9k , b 16k ve c 25k dir. a b 2c 172 ise 9k 16k 2.25k 172 9k 16k 50k 172 43k 172 k 4 k 2 dir. a b 3k 4k 7k 7.2 14 tür. Orantı Çeşitleri Doğru Orantı İki çokluktan biri artarken diğeri de artıyorsa veya biri azalırken diğeri de azalıyorsa doğru orantı vardır. x x ile y doğru orantılı ise şeklinde gösterilebilir. y Doğru orantı grafikleri ise aşağıdaki gibidir: Örnek: (x 2) sayısı (2y 3) sayısı ile doğru orantılıdır. x 4 iken y 3 ise x 6 iken y kaçtır? Çözüm: 4 3 6 x 2 k dır. İlk bilg iden k ‘ yı bulalım. 2y 3 x 2 6 2 k 2 dir. 2y 3 3 İkinci bilg iden y ‘ yi bulabiliriz artık. x 2 8 7 2 2 2y 3 4 y dir. 2y 3 2y 3 2 Not: a ile b ve c ile d doğru orantılı ise, a b c d D.O: a.d c.b dir. Çapraz çarpımları eşittir. Örnek: Bir araba 12 lt yakıt ile 200 km gitmektedir. 300 km uzunluğundaki bir yol için ne kadar yakıt gerekir? Çözüm: 12 lt 200 km x lt 300 km D.O: 12. 300 3 x. 200 2 dir. 36 2x x 18 lt dir. Not: Sadece “orantılıdır” diye belirtiliyorsa bundan doğru orantıyı anlayacağız. Örnek: x, y ve z sayıları sırasıyla 2, 3 ve 5 ile orantıldır. x 2y z 24 ise x y kaçtır? Çözüm: x y z k dır. 2 3 5 x 2y z 24 ise 2k 2.3k 5z 24 2k 6k 5k 24 3k 24 k 8 dir. x y 2k 3k k 8 dir. Örnek: www.matematikkolay.net Ali, Burak ve Ceyhun sırasıyla 21, 24 ve 27 yaşların – dadırlar. Kendilerine 240 000 TL miras kalmıştır ve yaşlarıyla orantılı olarak bunu paylaşmaya karar vermişlerdir. Burak ‘ın payı, Ceyhun’dan ne kadar eksiktir? Çözüm: A B C orantısını kurabiliriz.İşlemleri kolay – 21 24 27 laştımak için her tarafı 3 ile çarpalım. Paydalar küçülmüş olur. A B C olur. Bu orantının sabitine k diyelim. 7 8 9 A 7k, B 8k ve C 9k olur. Toplamları 240 000 TL olmalıdır. 7k 8k 9k 240 000 24k 240 000 k 10 000 TL dir. Ceyhun Burak 9k 8k k 10 000 TL dir. Ters Orantı İki çokluktan biri artarken diğeri azalıyorsa veya biri azalırken diğeri artıyorsa burada ters orantı vardır. x ile y ters orantılı ise x.y k şeklinde gösterebiliriz. Ters orantı grafikleri ise aşağıdaki gibidir: Örnek: (x 2) sayısı (y 3) sayısı ile ters orantılıdır. x 4 iken y 3 ise x 6 iken y kaçtır? Çözüm: 4 3 6 (x 2).(y 3) k şeklinde bir ilişki var dır. İlk önce k ‘ yı bulalım. (x 2).(y 3) 2.6 12 k 12 dir. İkinci bilg iden y ‘ yi bulabiliriz. (x 2).(y 3) 12 4.(y 3) 12 y 3 3 y 0 dır. Not: a ile b ve c ile d ters orantılı ise, a b c d T.O: a.b c.d dir. Yatay çarpımları eşittir. Örnek: 2 işçinin 6 saatte fayans döşediği bir zemini 3 işçi kaç saatte bitirebilirdi? Çözüm: 2 işçi 6 saat 3 işçi x saat T.O: 2.6 3.x 12 3x x 4 saattir. Örnek: x, y ve z sayıları sırasıyla 3,4 ve 6 ile ters orantılıdır. x y 2z 15 ise x kaçtır? Çözüm: 3x 4y 6z şeklinde bir eşitlik var dır. Bu eşitliği 3, 4 ve 6 nın en küçük ortak katına eşitle – yelim. EKOK(3, 4, 6) 12 dir. 3x 4y 6z 12k şeklinde yazarsak, x 4k, y 3k ve z 2k olur. Buna göre, x y 2z 15 4k 3 k 2.2k 15 4k 3k 4k 15 5k 15 k 3 tür. x 4.k 4.3 12 dir. Örnek: Bir traktörün ön tekerliğinin yarıçapının, arka teker- 3 leğinin yarıçapına oranı dir. Bu traktörün arka 8 tekerleği 75 kez döndüğünde ön tekerlek kaç kere dönmüştür ? www.matematikkolay.net Çözüm: İki tekerlek de aynı yolu gitmektedir. Tekerleğin yarıçapı azaldıkça, dönüş sayısı arta – caktır. Yani ters orantı var dır. Ön tekerleğin yarıçapı 3r iken, arka tekerleğin yarıçapı 8r olur. 8r 75 kez 3r x T.O: 8 r .75 3r .x 8. 75 25 3.x x 200 dür. Birleşik Orantı Birden fazla orantı varsa, bu bir birleşik orantıdır. x.z x ile y doğru, z ile ters orantılı ise k dır. y Örnek: (x 1) sayısı (y 2) sayısı ile doğru, (z 2) ile ters orantılıdır. x 4, y 3 iken z 6 olduğuna göre, x 2, y 4 iken z kaçtır? Çözüm: 4 6 3 2 4 x 1 (z 2) k şeklinde bir eşitlik var dır. y 2 İlk bilg iden k ‘ yı bulalım. x 1 5 (z 2) 4 4 k 4 tür. y 2 5 İkinci bilg ide z’ yi bulabiliriz. x 1 3 (z 2) 4 y 2 6 2 (z 2) 4 z 2 8 z 10 dur. Örnek: 1000 tane halıyı 4 makine günde 8 saat çalışarak 5 günde bitirmektedir. 1500 halıyı günde 12 saat çalışarak 5 makine kaç günde bitirir? Çözüm: Halı miktarı arttıkça gün sayısı artar .(Doğru Orantı) Makina sayısı arttıkça gün sayısı azalır .(Ters Orantı) Günlük çalışma saati arttıkça gün sayısı azalır .(T.O.) 1000 halı 4 makina 8 saat 5 gün 1500 halı 5 makina 12 saat x gün 1000 2 . 5.12.x 1500 3 .4.8. 5 eşitliğini kurabiliriz. 24x 96 x 4 gün buluruz. 1. Yapılan İş 2. Yapılan İş Bu işle ilgili diğer bilgiler Bu işle ilgili diğer bilgiler II. Yol : 1000 2 1500 04.08.2005 3 6.9.x 2 4 2 3 .8.5 05.Ara 4 .x 02.Ağu 2 . 5 5. 4 .x x 4 günde bitirir. Örnek: a ve b sayıları sırasıyla 3 ve 4 ile doğru, c sayısı ise 2 ile ters orantılıdır. 3a2b c 12 ise b kaçtır? Çözüm: 6c 8c a b 2c şeklinde eşitlik kurabiliriz. 3 4 a 6c ve b 8c dir. 3a 2b c 12 ise 18c 16c c 12 3c 12 c 4 tür. b 8c 8.4 32 dir. Aritmetik Ortalama n tane sayının toplamını n’ye bölersek aritmetik ortalamayı buluruz. 1 2 n x x … x Aritmetik Ortalama dir. n www.matematikkolay.net Örnek: 3 öğrenci bir sınavda 100, 104 ve 111 net yapmışlardır. O halde, ortalama kaç net yapmışlardır? Çözüm: 100 104 111 315 105 tir. 3 5 Not: n tane sayının aritmetik ortalaması x ise, bu sayıların toplamı n.x tir. Örnek: 5 kişilik bir grubun yaş ortalaması 22 dir. Bu gruba yaş ortalaması 29 olan iki kişi katılırsa yeni yaş ortalaması kaç olur? Çözüm: 5 kişinin yaşları toplamı 5.22 110 dur. Sonradan gelen 2 kişinin yaşları toplamı 2.29 58 O halde 7 kişinin yaşları toplamı 110 58 168 dir. 168 Yeni Ortalama 24 tür. 7 Not: n tane sayının aritmetik ortalaması x ise, bu sayıların her biri A ile çarpılıp, her birine B eklenirse yeni ortalama Ax+B olur. Örnek: Anne, baba ve 2 çocuktan oluşan 4 kişilik bir ailenin yaş ortalaması 25 tir. 5 yıl sonra yaş ortalaması kaç olur? Çözüm: Her biri 5’er yaş artacağı için yeni yaş ortalaması 255 30 olur. Geometrik Ortalama n tane sayının çarpımını n.dereceden kökünü alırsak, geometrik ortalamayı buluruz. n 1 2 n Geometrik Ortalama x .x …x dir. Örnek: x 4 ve 9’un geometrik ortalaması y 4, 9 ve 48’in geometrik ortalaması x olmak üzere, kaçtır? y Çözüm: 3 3 2 2 3 2 2 4 3 6 3 2 x 4.9 36 6 6 y 4.9.48 2 .3 .16.3 2 .3 .2 .3 2 .3 6 6 1 dir. 2 .3 12 2 Not: Aritmetik ortalaması ile geometrik ortalaması eşit olan iki sayı birbirine eşittir. Örnek: 3a b 12 ile a b 8 in aritmetik ortalaması ile geometrik ortalaması birbirine eşit ise a ile b nin aritmetik ortalaması kaçtır? Çözüm: Bu sayılar birbirine eşittir. 3a b 12 a b 8 2a 2b 20 a b 10 dur. a ile b nin aritmetik ortalaması a b 10 5 tir. 2 2 Orta Orantılı 2 a ve b pozitif olmak üzere, a x x sayısı, a ve b nin orta orantılısıdır. x b x a.b x a.b dir. Örnek: 3 ile 12 nin orta orantılısı x olduğuna göre, x ile 12 nin aritmetik ortalaması kaçtır? Çözüm: 2 3 x x 36 x 6 dır. x 12 x ile 12 nin aritmetik ortalaması x 12 6 12 18 9 dur. 2 2 2

