Toplam ve fark durumundaki ifadelerin çarpım şeklinde gösterilmesine çarpanlara ayırma denir.
Ortak Çarpan Parantezine Alma
Verilen terimlerde aynı çarpanlar varsa, paranteze alınarak çarpanlarına ayrılabilir.
Örneğin, 5a+5b=5(a+b)
ax-bx+cx=x(a-b+c) gibi.
Örnek:
Çözüm:
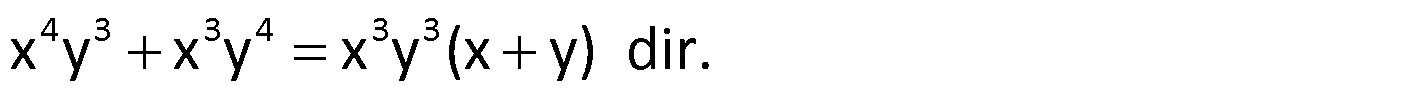
Örnek:
Çözüm:
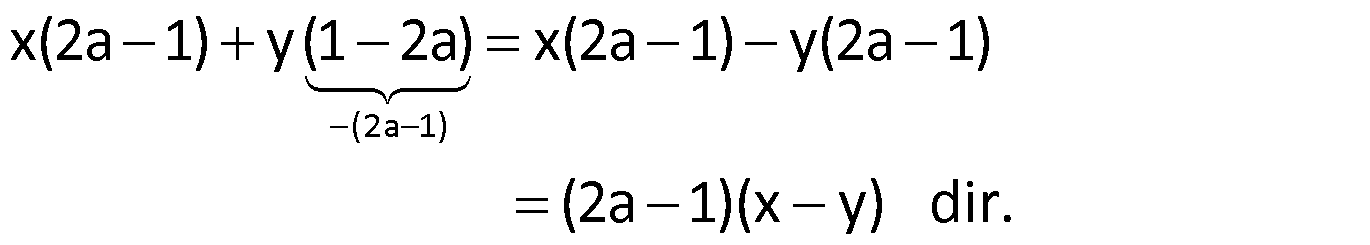
Gruplandırarak Çarpanlara Ayırma
Dört veya daha fazla terimli ifadelerde, hepsinde ortak çarpan yoksa terimler ikili, üçlü gibi gruplandırılarak çarpanlara ayrılmaya çalışılır. Örneğin,
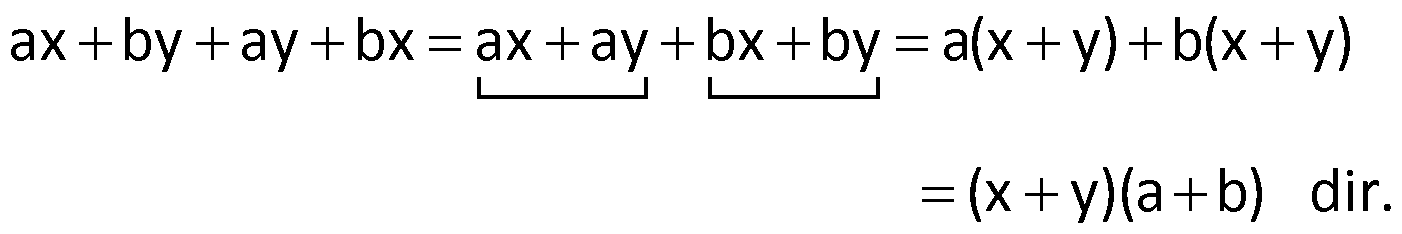
Örnek:
Çözüm:
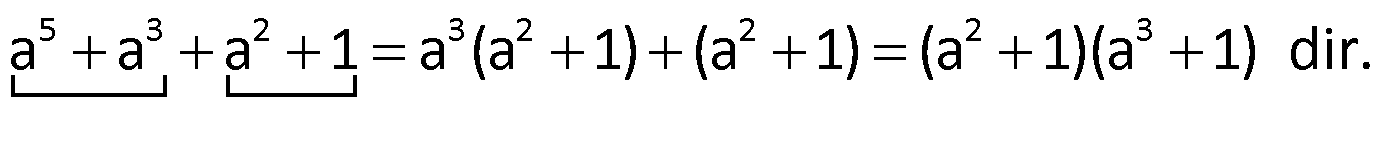
Örnek:
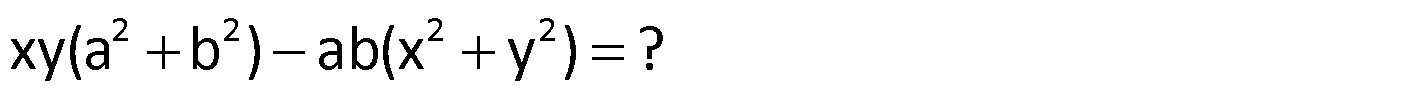
Çözüm:
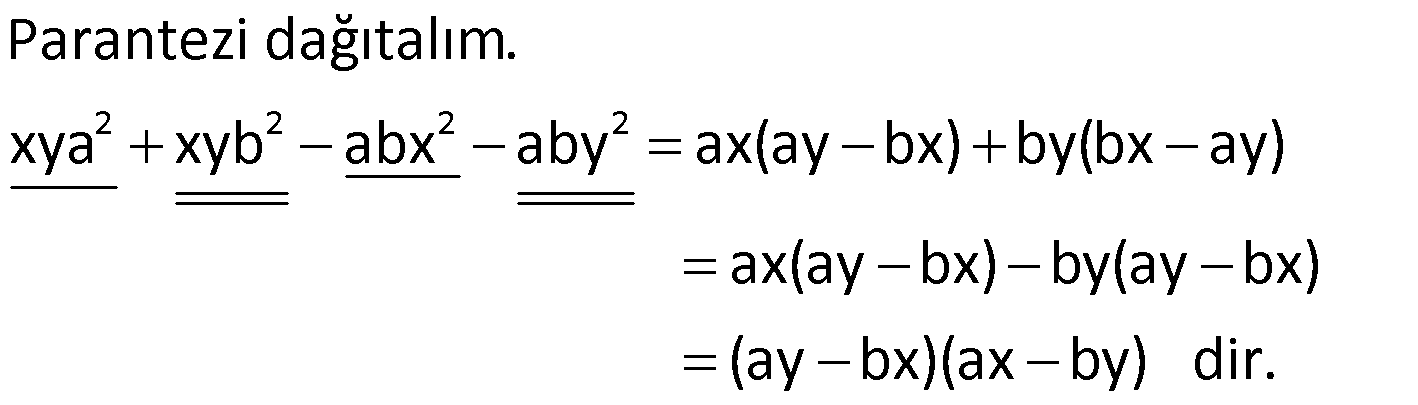
Özdeşlik Kullanarak Çarpanlara Ayırma
Tam Kare Özdeşliği
Örnek:
Çözüm:
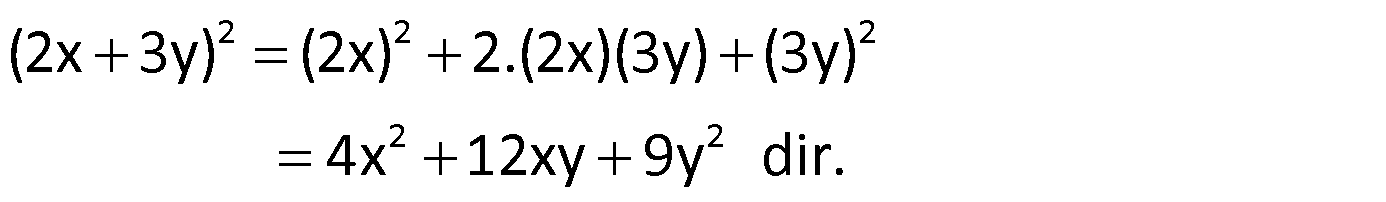
Örnek:
Çözüm:
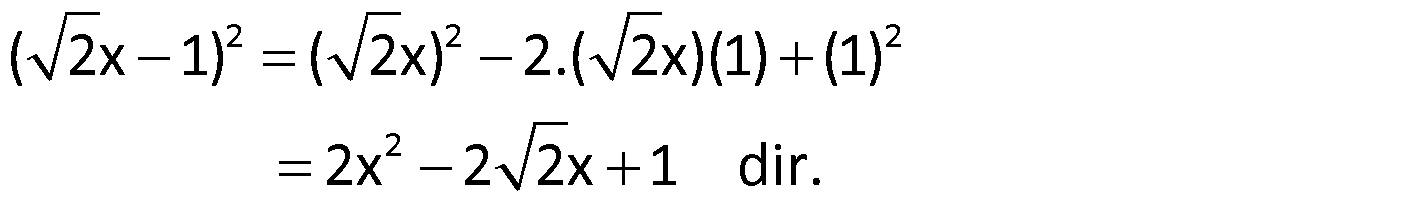
Örnek:
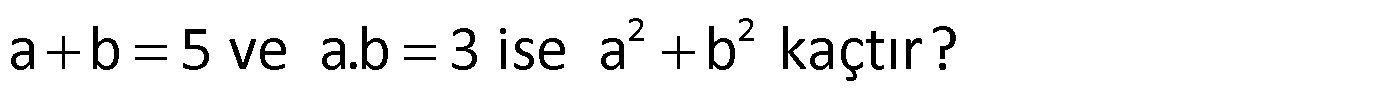
Çözüm:
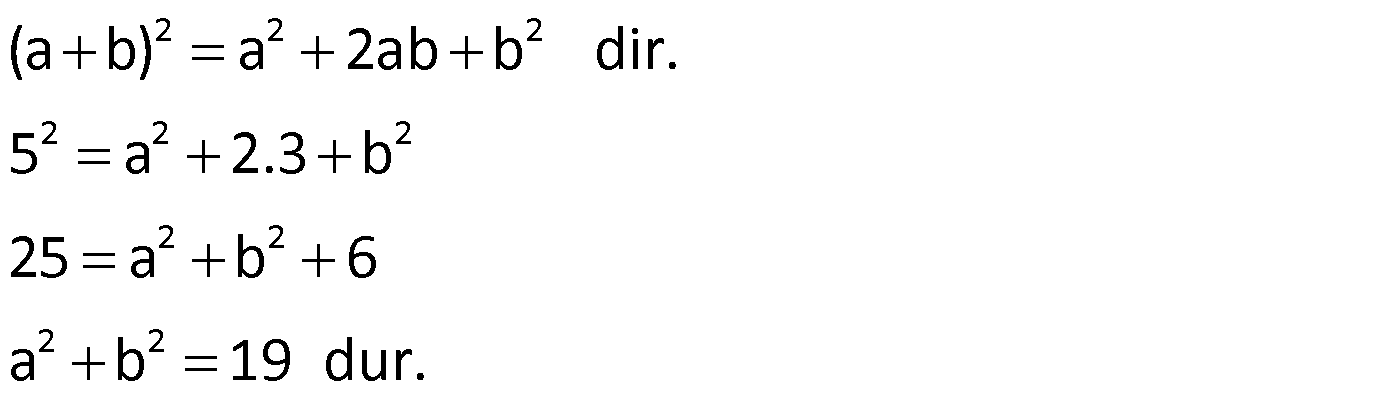
Not:
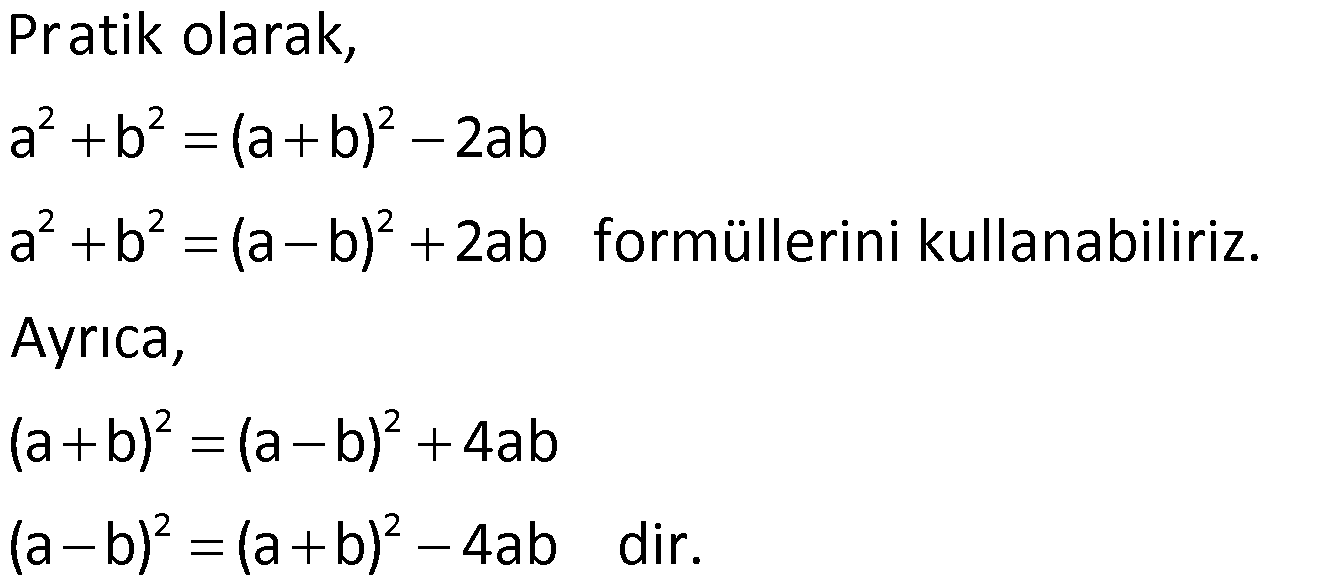
Örnek:
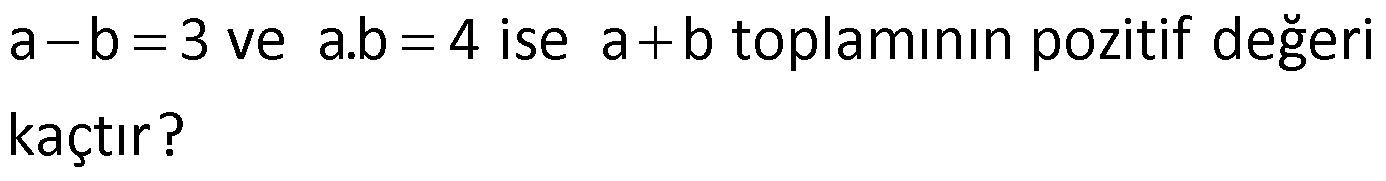
Çözüm:
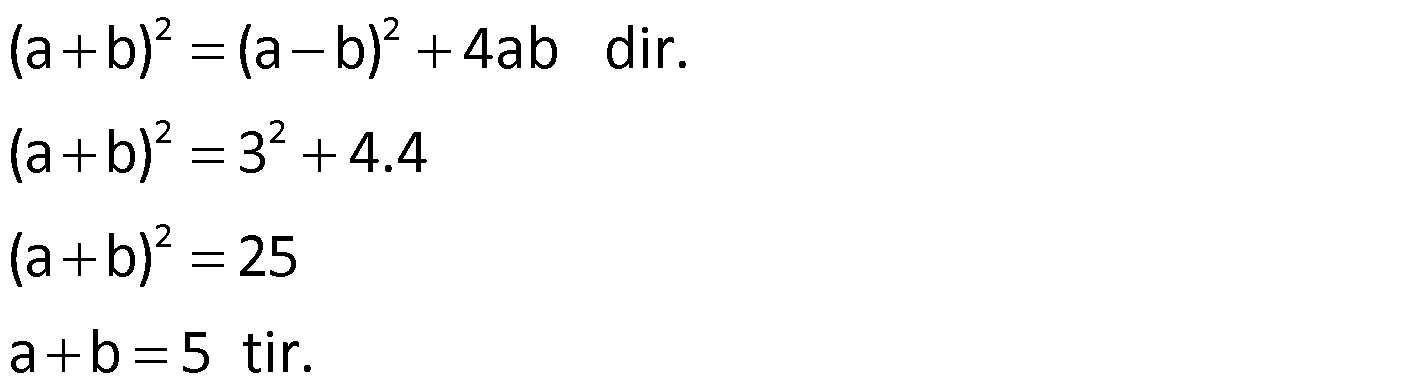
Örnek:
Çözüm:
Uyarı
Örnek:
Çözüm:
Üç Terimin Karesi
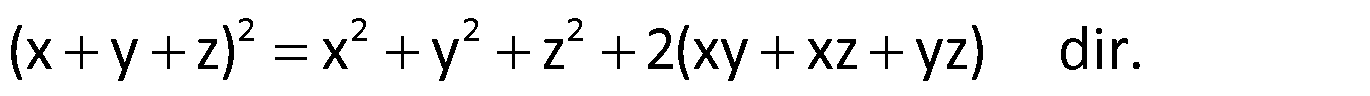
Bunu kullanarak
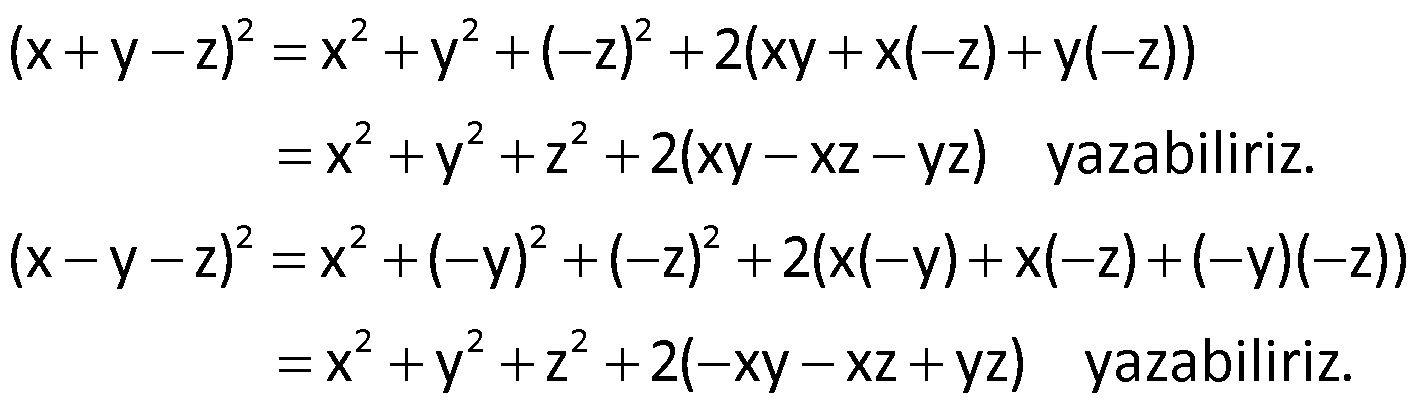
Örnek:
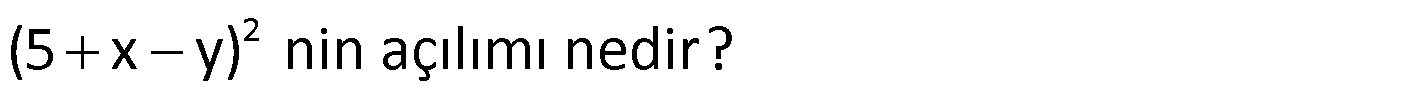
Çözüm:
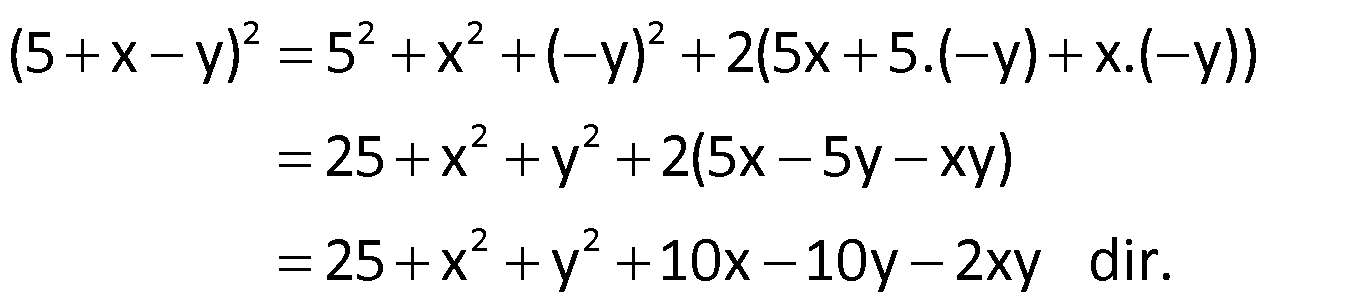
İki Kare Farkı
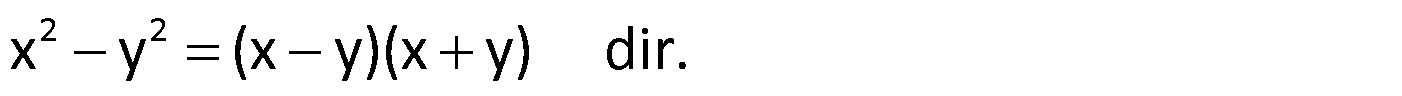
Örnek:
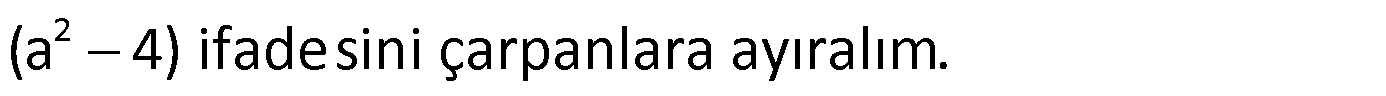
Çözüm:
Örnek:
Çözüm:
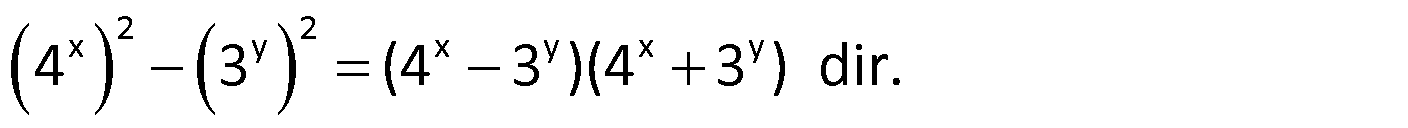
Örnek:
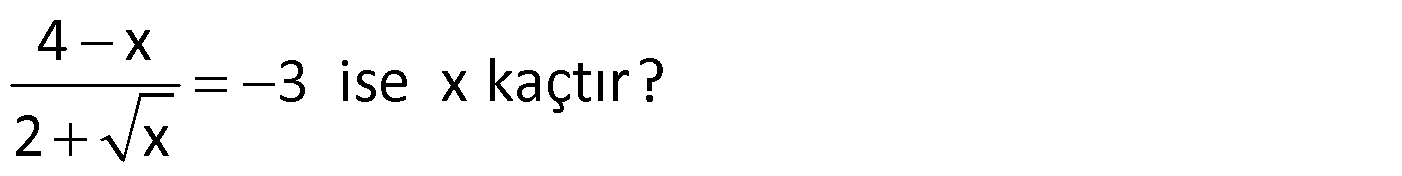
Çözüm:
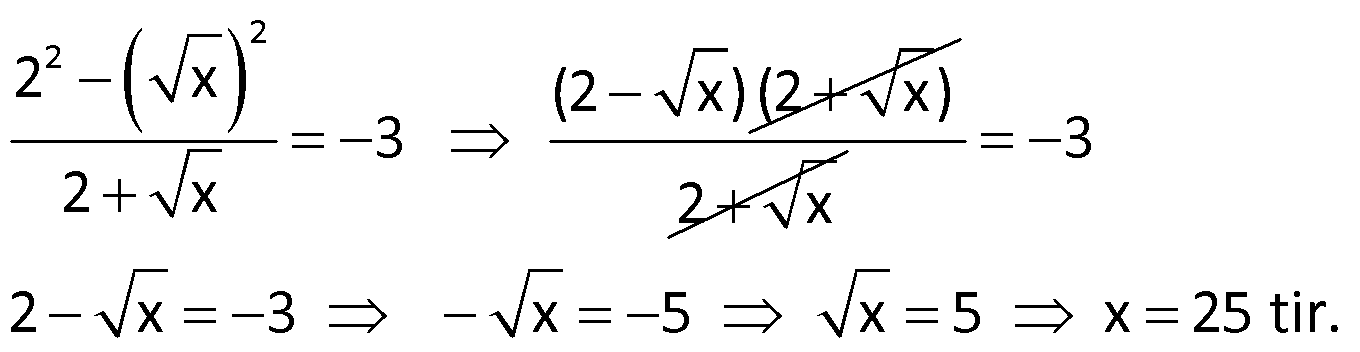
Örnek:
Çözüm:
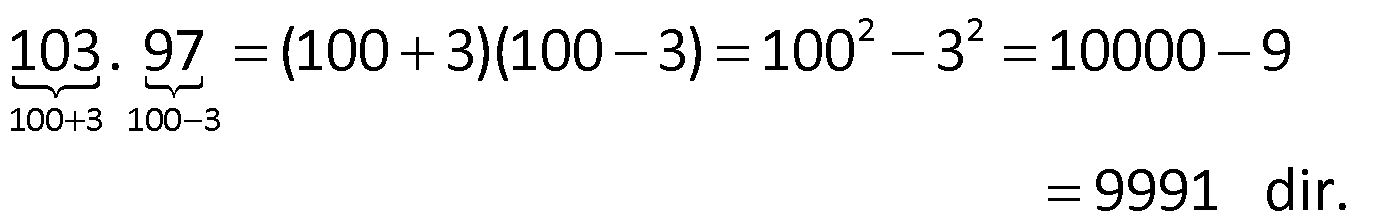
Örnek:
Çözüm:
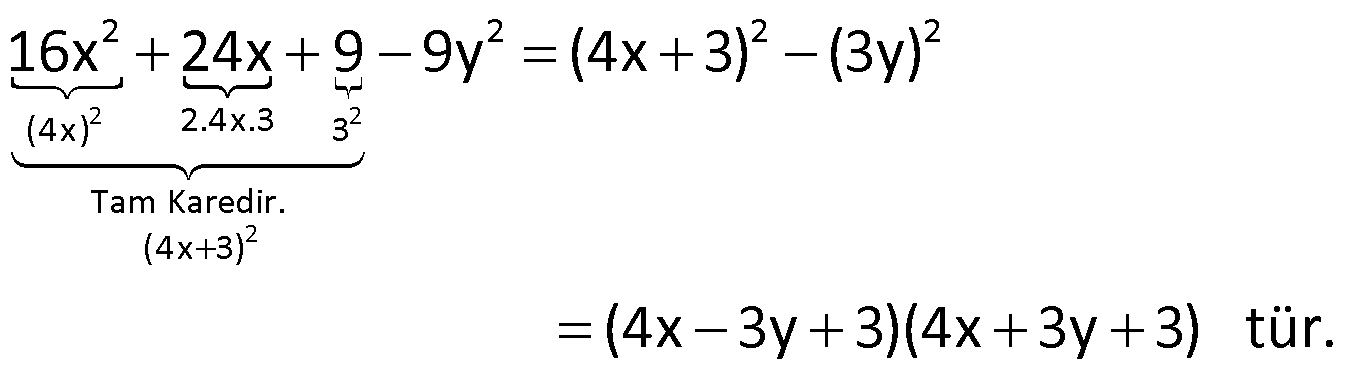
İki Terimin Toplamının ve Farkının Küpü
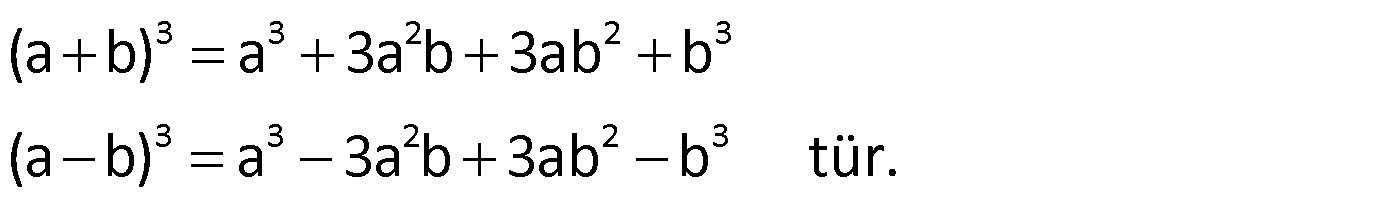
Örnek:
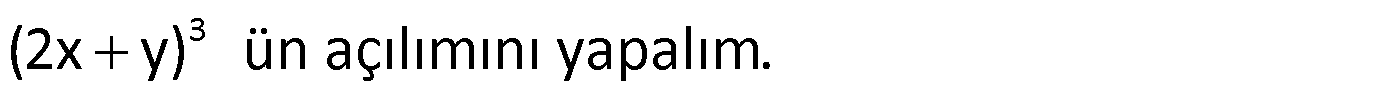
Çözüm:
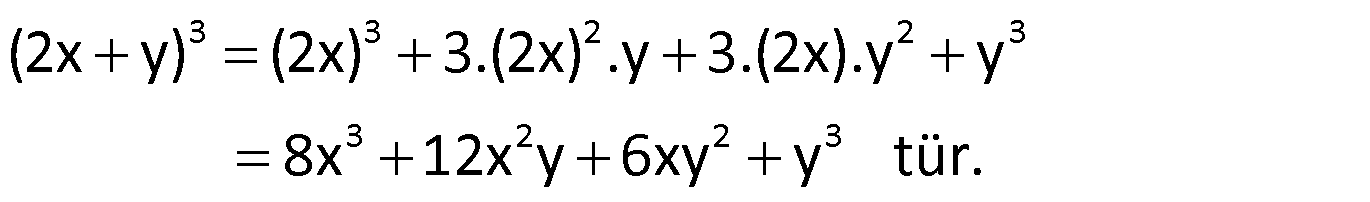
Örnek:
Çözüm:
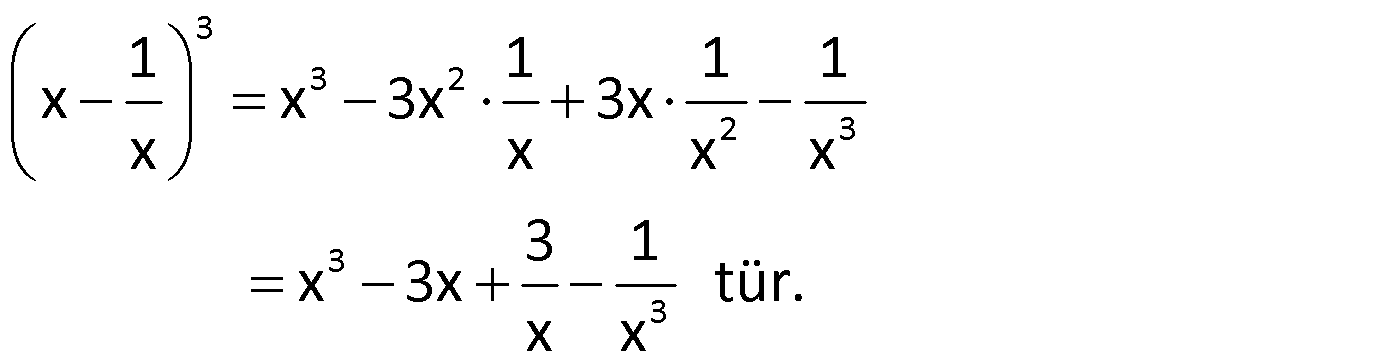
İki Küp Toplamı ve İki Küp Farkı
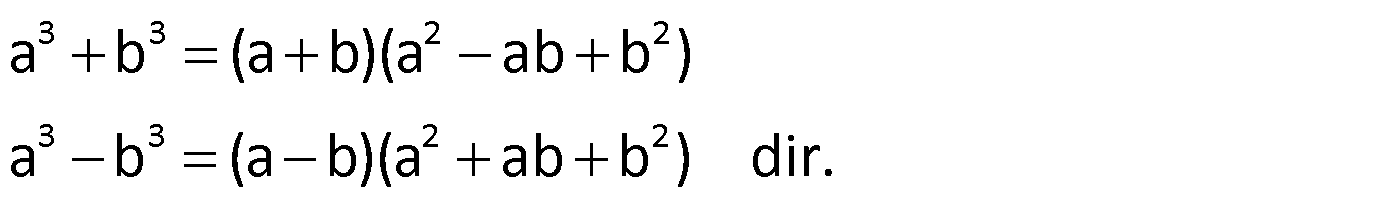
Örnek:
Çözüm:
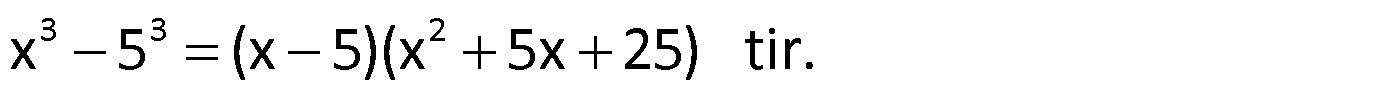
Not:
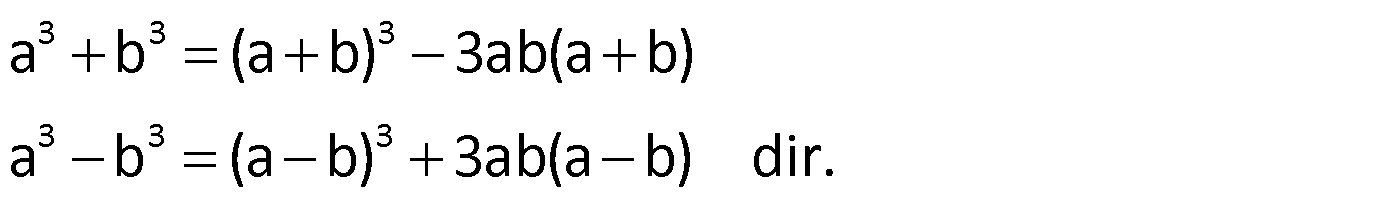
Örnek:
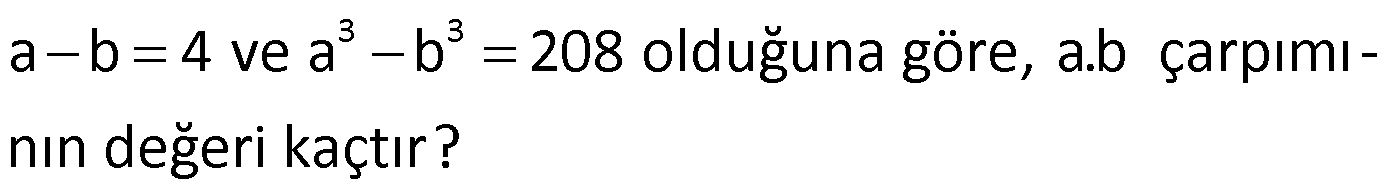
Çözüm:
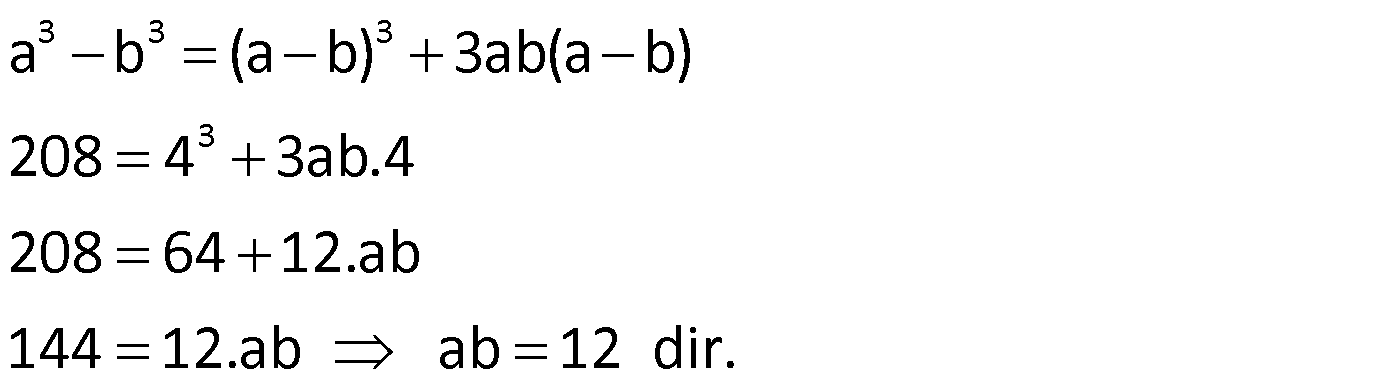
Üç Terimli İfadeleri Çarpanlara Ayırma
nin katsayını oluşturan çarpanlar ile sabit terimi oluşturan çarpanlar, çapraz çarpılıp toplandığında x’in katsayını veriyorsa, aşağıdaki gibi çarpanlarına ayrılabilir.
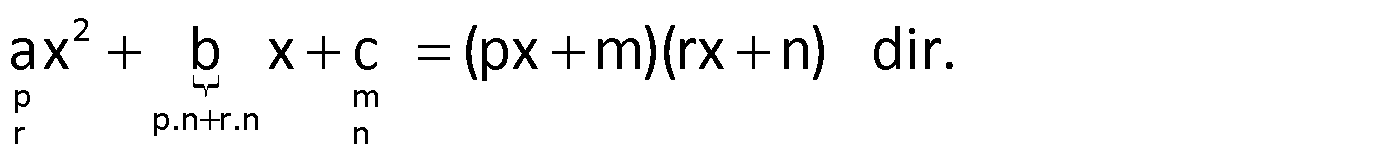
Örnek:
Çözüm:
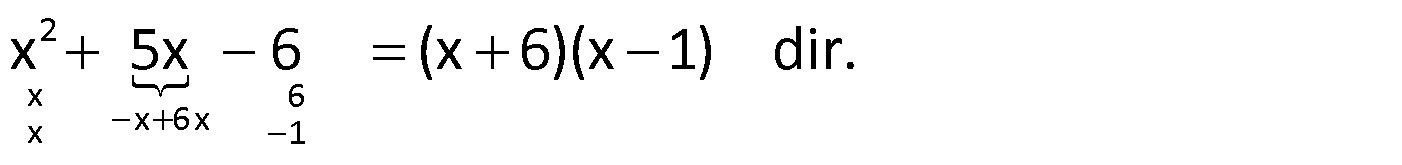
Örnek:
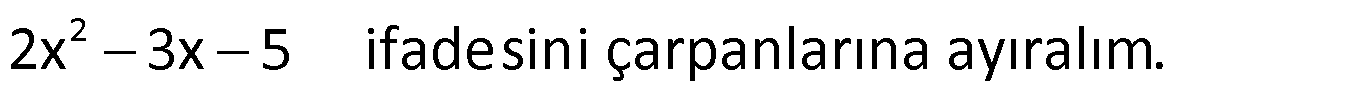
Çözüm:
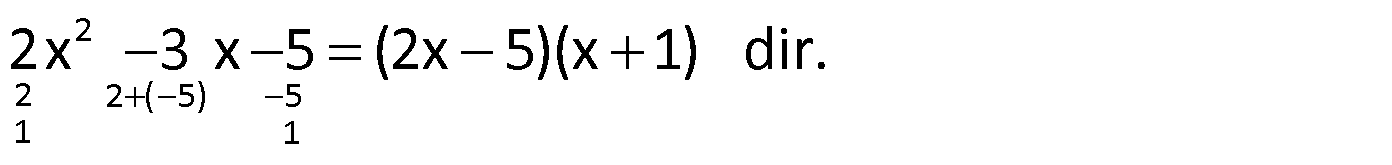
Örnek:
Çözüm:
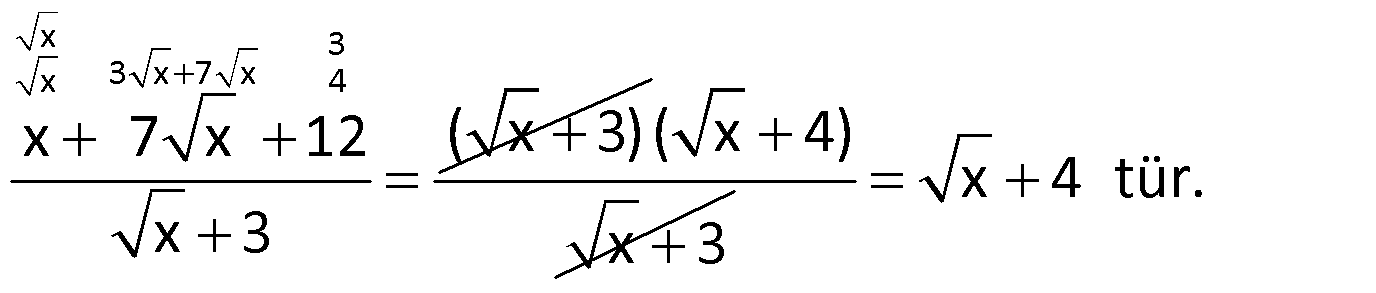
Değişken Değiştirerek Çarpanlarına Ayırma
Aynı karışık ifadeler için tek bir değişken kullanarak daha kolay çarpanlarına ayırabiliriz.
Örnek:
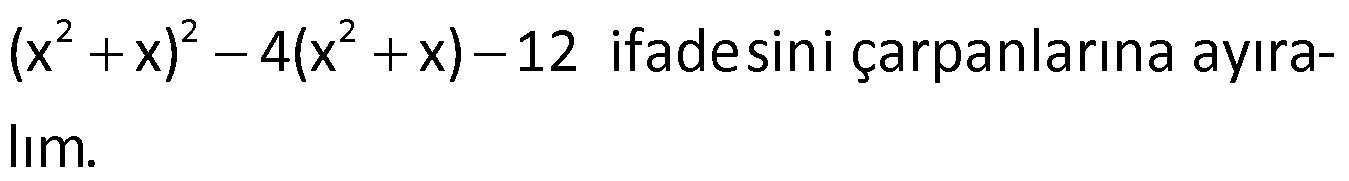
Çözüm:
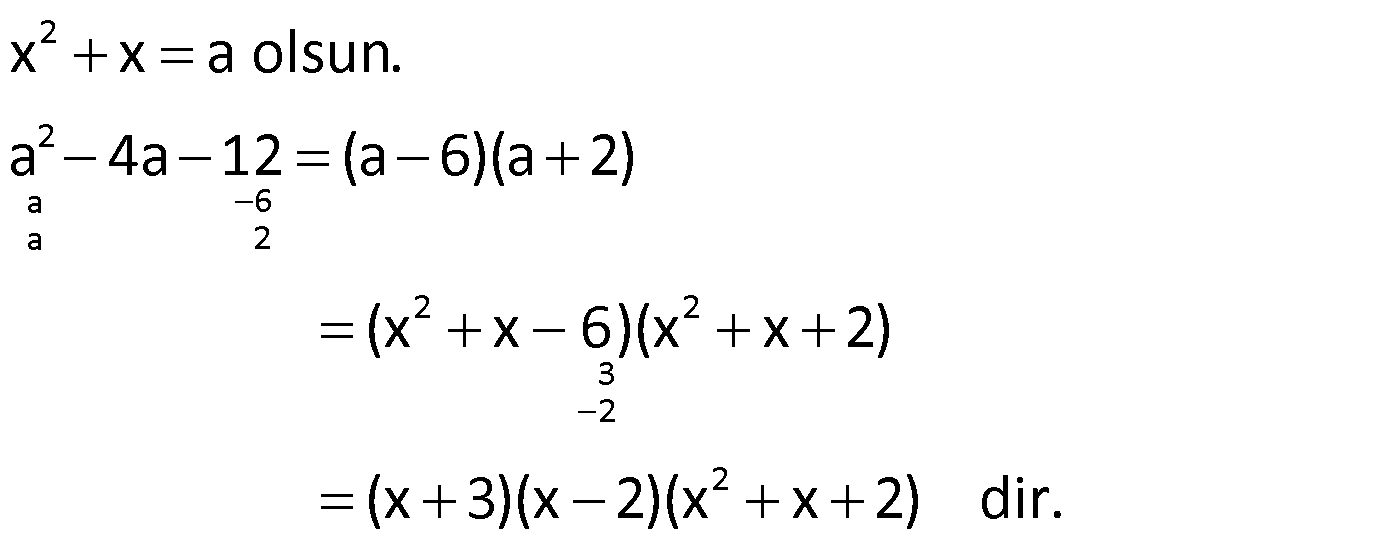
Rasyonel İfadeler
P(x) ve Q(x) birer polinom ve 
olmak üzere 
şeklindeki ifadelere rasyonel ifadeler denir. Çarpanlarına ayırarak, bu ifadeleri sadeleştirmek mümkün.
Örnek:
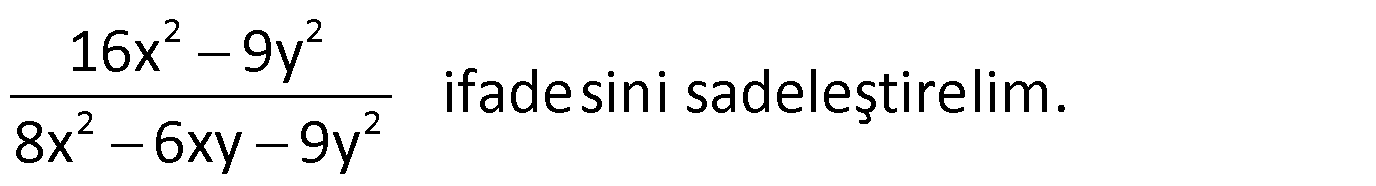
Çözüm:
Konu ile ilgili Çözümlü Sorular veya Çıkmış Sorular için Tıkla
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)ÇARPANLARA AYIRMA KONU ANLATIMI www.matematikkolay.net Toplam ve fark durumundaki ifadelerin çarpım şeklinde gösterilmesine çarpanlara ayırma denir. Ortak Çarpan Parantezine Alma Verilen terimlerde aynı çarpanlar varsa, paranteze alınarak çarpanlarına ayrılabilir. Örneğin, 5a+5b=5(a+b) ax-bx+cx=x(a-b+c) gibi. Örnek: 4 3 3 4 x y x y ? Çözüm: 4 3 3 4 3 3 x y x y x y (x y) dir. Örnek: x(2a1)y(12a) ? Çözüm: (2a 1) x(2a 1) y(1 2a) x(2a 1) y(2a 1) (2a 1)(x y) dir. Gruplandırarak Çarpanlara Ayırma Dört veya daha fazla terimli ifadelerde, hepsinde ortak çarpan yoksa terimler ikili, üçlü gibi gruplandırılarak çarpanlara ayrılmaya çalışılır. Örneğin, ax by ay bx ax ay bx by a(x y) b(x y) (x y)(a b) dir. Örnek: 5 3 2 a a a 1? Çözüm: 5 3 2 3 2 2 2 3 a a a 1 a (a 1)(a 1) (a 1)(a 1) dir. Örnek: 2 2 2 2 xy(a b )ab(x y ) ? Çözüm: 2 2 2 2 Parantezi dağıtalım. xya xyb abx aby ax(ay bx) by(bx ay) ax(ay bx) by(ay bx) (ay bx)(ax by) dir. Özdeşlik Kullanarak Çarpanlara Ayırma Tam Kare Özdeşliği 2 2 2 2 2 2 (x y) x 2xy y (x y) x 2xy y Örnek: 2 (2x 3y) ? Çözüm: 2 2 2 2 2 (2x 3y) (2x) 2.(2x)(3y) (3y) 4x 12xy 9y dir. Örnek: 2 ( 2x 1) ? Çözüm: 2 2 2 2 ( 2x 1) ( 2x) 2.( 2x)(1) (1) 2x 2 2x 1 dir. Örnek: 2 2 ab 5 ve a.b 3 ise a b kaçtır? Çözüm: 2 2 2 2 2 2 2 2 2 2 (a b) a 2ab b dir. 5 a 2.3 b 25 a b 6 a b 19 dur. ÇARPANLARA AYIRMA KONU ANLATIMI www.matematikkolay.net Not: 2 2 2 2 2 2 2 2 2 2 Pratik olarak, a b (a b) 2ab a b (a b) 2ab formüllerini kullanabiliriz. Ayrıca, (a b) (a b) 4ab (a b) (a b) 4ab dir. Örnek: a b 3 ve a.b 4 ise a b toplamının pozitif değeri kaçtır? Çözüm: 2 2 2 2 2 (a b) (a b) 4ab dir. (a b) 3 4.4 (a b) 25 a b 5 tir. Örnek: 2 4a 4a 1 ifadesini çarpanlarına ayıralım. Çözüm: 2 2 4a “2a” nın karesidir. 1 “1” in karesidir. 4a 2.(2a).(1) çarpımıdır. Ohalde bu ifade tam karedir. (2a 1) dir. Uyarı 2 2 2 2 2 2 2 2 2 2 (a b) ile a b aynı şey değildir. (a b) ile de a b aynı şey değildir. Örneğin, (3 5) 8 64 tür. Tamamen farklılar. 3 5 9 25 34 tür. Örnek: 2 2 x xy 4y ifadesini çarpanlarına ayıralım. 16 Çözüm: 2 2 2 x x ün karesidir. 16 4 4y “2y” nin karesidir. x xy 2. .(2y) çarpımıdır. 4 Ohalde bu ifade tam karedir. x 2y dir. 4 Üç Terimin Karesi 2 2 2 2 (x y z) x y z 2(xy xzyz) dir. Bunu kullanarak 2 2 2 2 2 2 2 2 2 2 2 2 2 2 (x y z) x y ( z) 2(xy x( z) y( z)) x y z 2(xy xz yz) yazabiliriz. (x y z) x ( y) ( z) 2(x( y) x( z) ( y)( z)) x y z 2( xy xz yz) yazabiliriz. Örnek: 2 (5x y) nin açılımı nedir? Çözüm: 2 2 2 2 2 2 2 2 (5 x y) 5 x ( y) 2(5x 5.( y) x.( y)) 25 x y 2(5x 5y xy) 25 x y 10x 10y 2xy dir. İki Kare Farkı 2 2 x y (x y)(x y) dir. Örnek: 2 (a 4) ifadesini çarpanlara ayıralım. ÇARPANLARA AYIRMA KONU ANLATIMI www.matematikkolay.net Çözüm: 2 2 a 2 (a2)(a2) dir. Örnek: x y (16 9 ) ifadesini çarpanlara ayıralım. Çözüm: x 2 y 2 x y x y 4 3 (4 3 )(4 3 ) dir. Örnek: 4 x 3 ise x kaçtır? 2 x Çözüm: 2 22 x (2 x) (2 x) 3 2 x 2 x 3 2 x 3 x 5 x 5 x 25 tir. Örnek: 103.97 çarpımı kaçtır? Çözüm: 2 2 100 3 100 3 103. 97 (100 3)(100 3) 100 3 10000 9 9991 dir. Örnek: 2 2 16x 9y 24x 9 ifadesini çarpanlarına ayıralım. Çözüm: 2 2 2 2 2 2 2 (4x) 2.4x.3 3 Tam Karedir. (4x 3) 16x 24x 9 9y (4x 3) (3y) (4x 3y 3)(4x 3y 3) tür. İki Terimin Toplamının ve Farkının Küpü 3 3 2 2 3 3 3 2 2 3 (a b) a 3a b 3ab b (a b) a 3a b 3ab b tür. Örnek: 3 (2x y) ün açılımını yapalım. Çözüm: 3 3 2 2 3 3 2 2 3 (2x y) (2x) 3.(2x) .y 3.(2x).y y 8x 12x y 6xy y tür. Örnek: 3 1 x ün açılımını yapalım. x Çözüm: 3 3 2 2 3 3 3 1 1 1 1 x x 3x 3x x x x x 3 1 x 3x tür. x x İki Küp Toplamı ve İki Küp Farkı 3 3 2 2 3 3 2 2 a b (a b)(a ab b ) a b (a b)(a ab b ) dir. Örnek: 3 x 125 ifadesini çarpanlarına ayıralım. ÇARPANLARA AYIRMA KONU ANLATIMI www.matematikkolay.net Çözüm: 3 3 2 x 5 (x 5)(x 5x 25) tir. Not: 3 3 3 3 3 3 a b (a b) 3ab(a b) a b (a b) 3ab(a b) dir. Örnek: 3 3 a b 4 ve a b 208 olduğuna göre, a.b çarpımı – nın değeri kaçtır? Çözüm: 3 3 3 3 a b (a b) 3ab(a b) 208 4 3ab.4 208 64 12.ab 144 12.ab ab 12 dir. Üç Terimli İfadeleri Çarpanlara Ayırma 2x nin katsayını oluşturan çarpanlar ile sabit terimi oluşturan çarpanlar, çapraz çarpılıp toplandığında x’in katsayını veriyorsa, aşağıdaki gibi çarpanlarına ayrılabilir. 2 p m r p.n r.n n ax b x c (px m)(rx n) dir. Örnek: 2 x 5x 6 ifadesini çarpanlarına ayıralım. Çözüm: 2 x 6 x x 6x 1 x 5x 6 (x 6)(x 1) dir. Örnek: 2 2x 3x 5 ifadesini çarpanlarına ayıralım. Çözüm: 2 2 2 ( 5) 5 1 1 2x 3 x 5 (2x 5)(x 1) dir. Örnek: x 7 x 12 ifadesinin en sade hali nedir? x 3 Çözüm: x 3 x 3 x 7 x 4 x 7 x 12 ( x 3) x 3 ( x 4) x 3 x 4 tür. Değişken Değiştirerek Çarpanlarına Ayırma Aynı karışık ifadeler için tek bir değişken kullanarak daha basit olarak çarpanlarına ayırabiliriz. Örnek: 2 2 2 (x x) 4(x x) 12 ifadesini çarpanlarına ayıralım. Çözüm: 2 2 a 6 a 2 2 2 3 2 2 x x a olsun. a 4a 12 (a 6)(a 2) (x x 6)(x x 2) (x 3)(x 2)(x x 2) dir. Rasyonel İfadeler P(x) ve Q(x) birer polinom ve Q(x) 0 olmak üzere P(x) Q(x) şeklindeki ifadelere rasyonel ifadeler denir. Çarpanlarına ayırarak, bu ifadeleri sadeleştirmek mümkün. Örnek: 2 2 2 2 16x 9y ifadesini sadeleştirelim. 8x 6xy 9y Çözüm: 2 2 2 2 2 2 2 4x 6 12 6 3y 2x 3y 16x 9y 4x 3y İki Kare Farkı 8x 6xy 9y (4x 3y)(2x 3y) ax bx c (4x 3y) 4x 3y (4x 3y) 4x 3y dir. (2x 3y) 2x 3y
