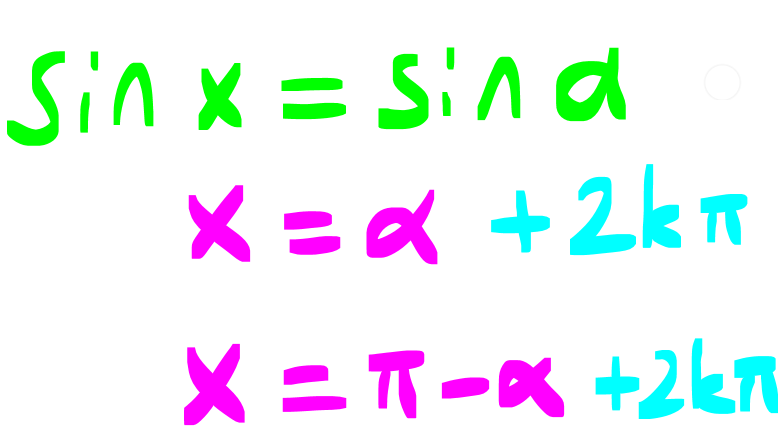Bu bölümde Trigonometrik Denklemler ile ilgili 16 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
Çözüm için Tıklayınız.
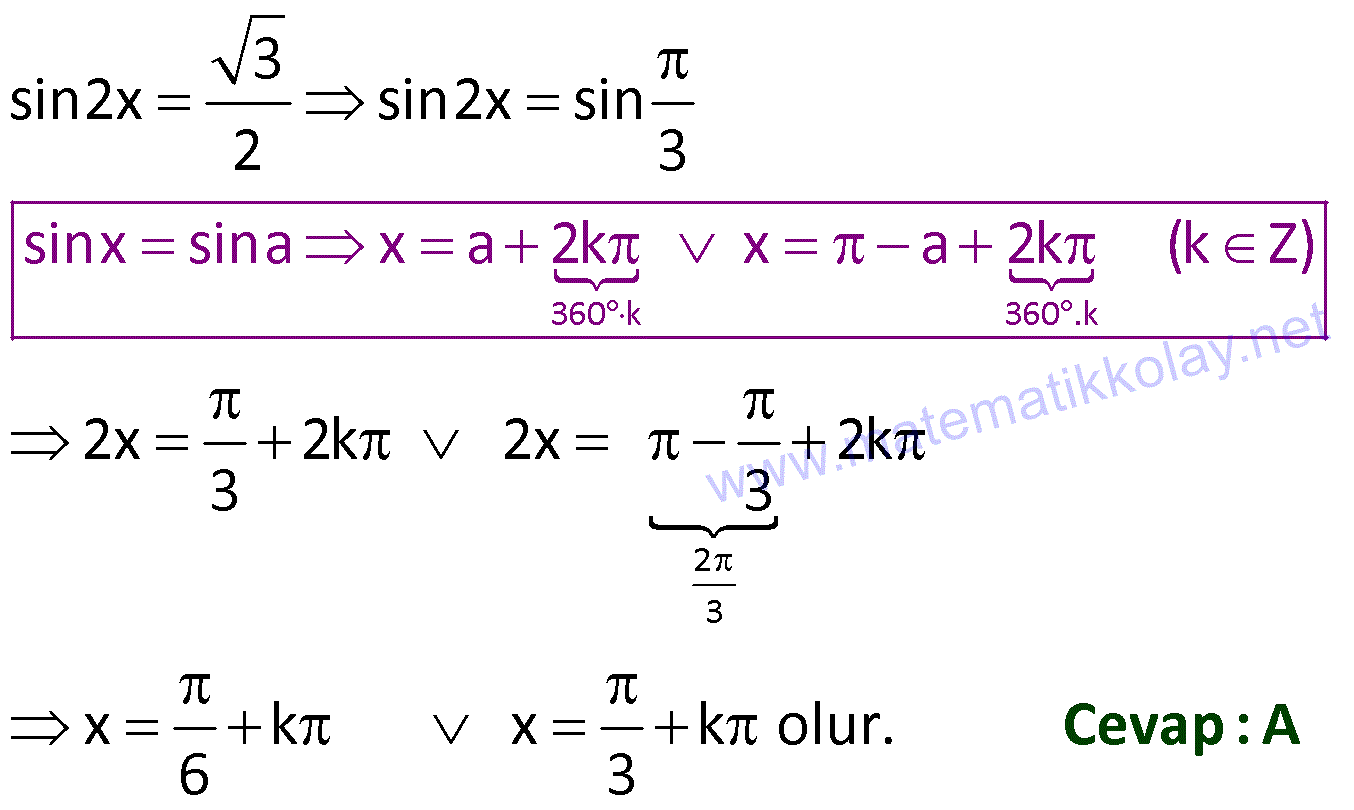
2.SORU
| | | | | |
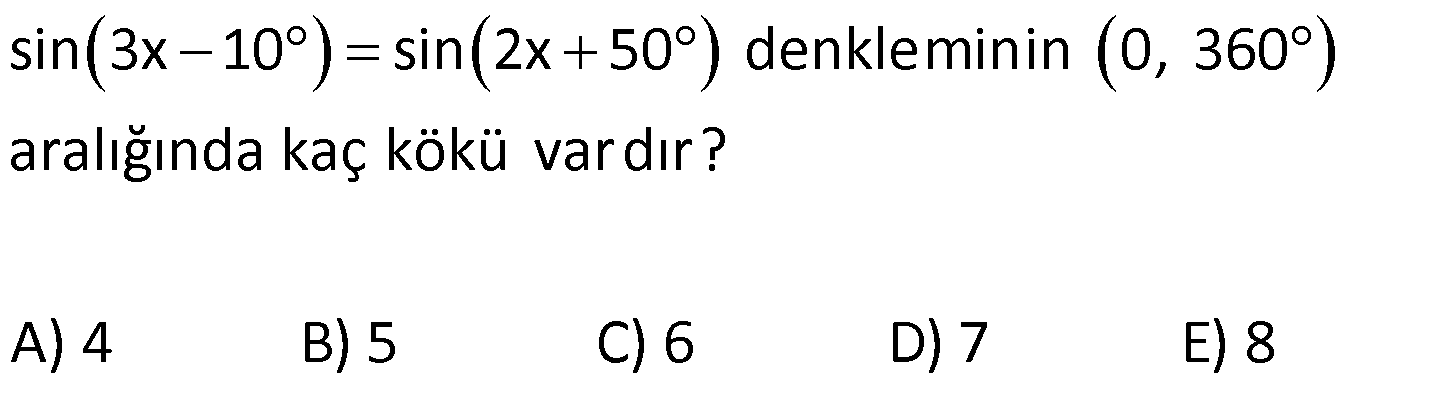
Çözüm için Tıklayınız.
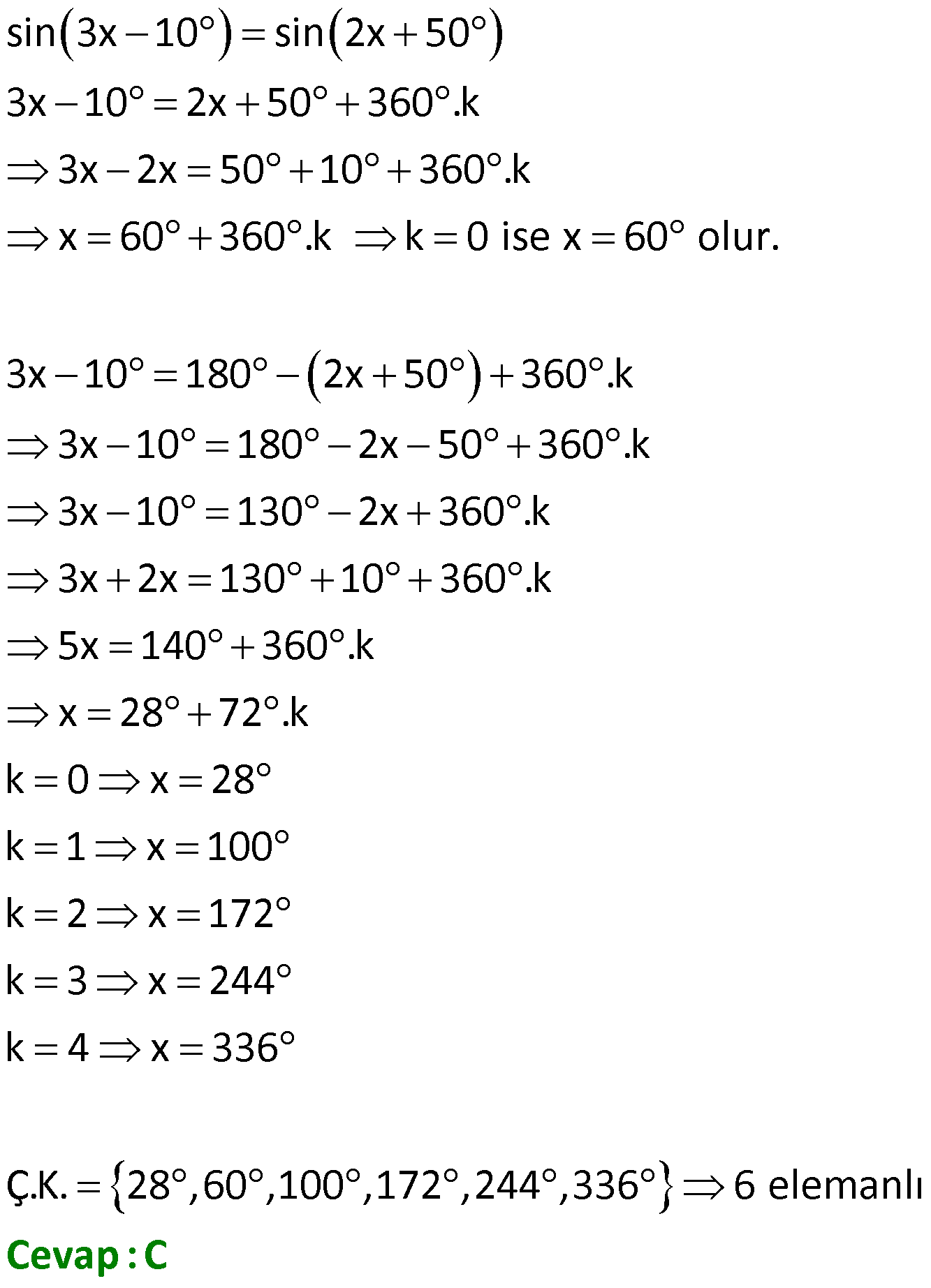
3.SORU
| | | | | |
Çözüm için Tıklayınız.
4.SORU
| | | | | |
Çözüm için Tıklayınız.
5.SORU
| | | | | |
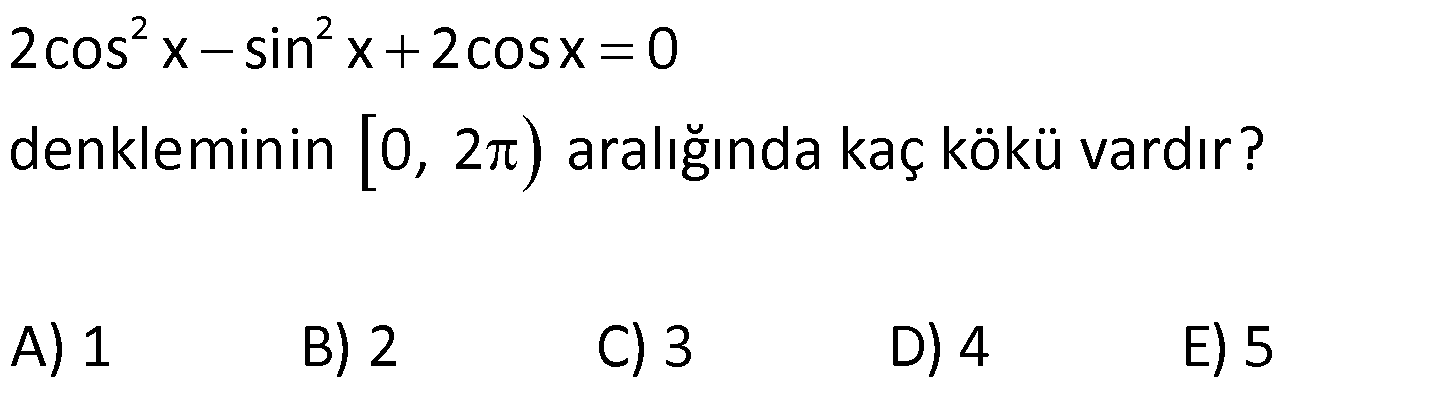
Çözüm için Tıklayınız.
6.SORU
| | | | | |
Çözüm için Tıklayınız.
7.SORU
| | | | | |
Çözüm için Tıklayınız.
8.SORU
| | | | | |
Çözüm için Tıklayınız.
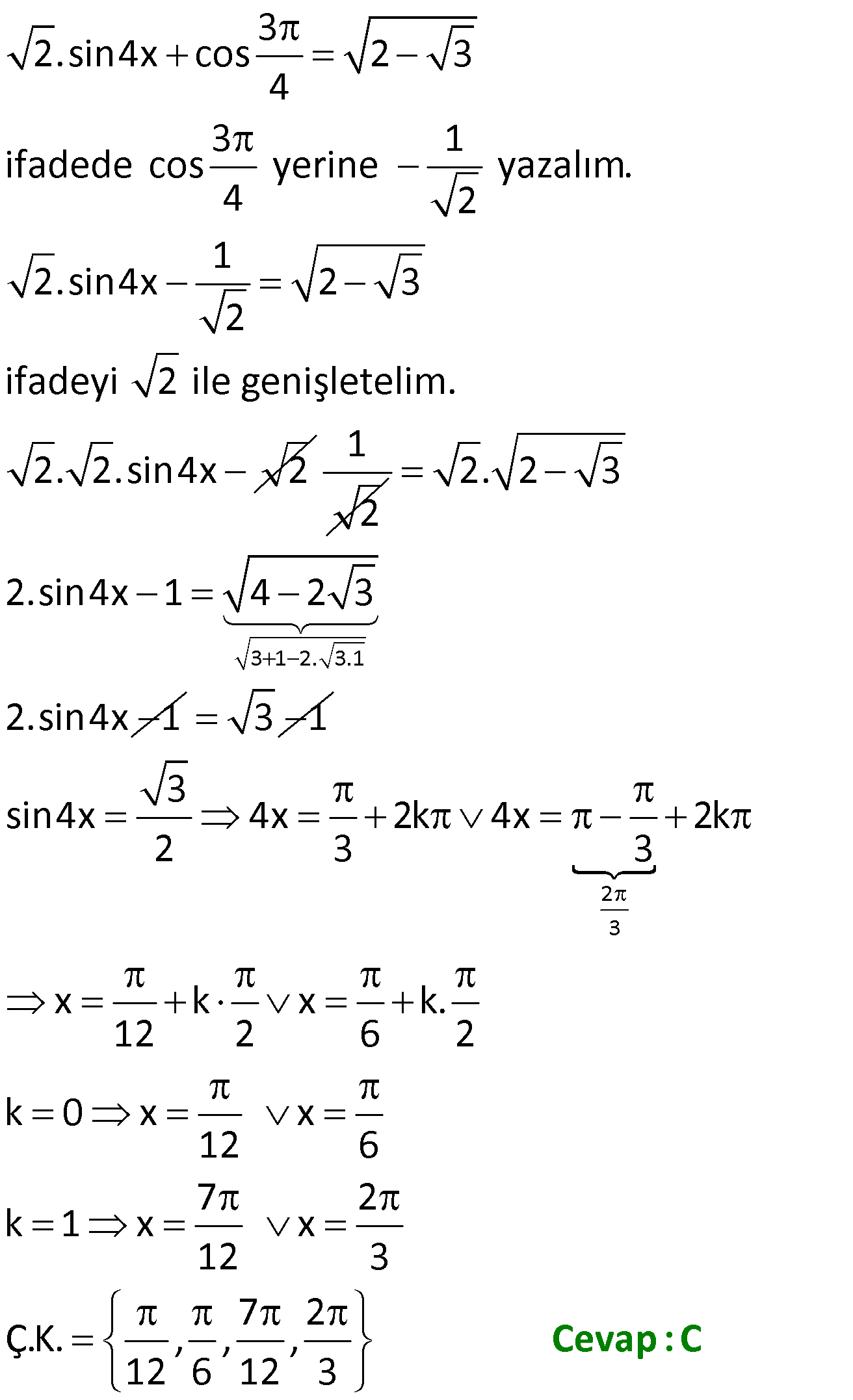
9.SORU
| | | | | |
Çözüm için Tıklayınız.
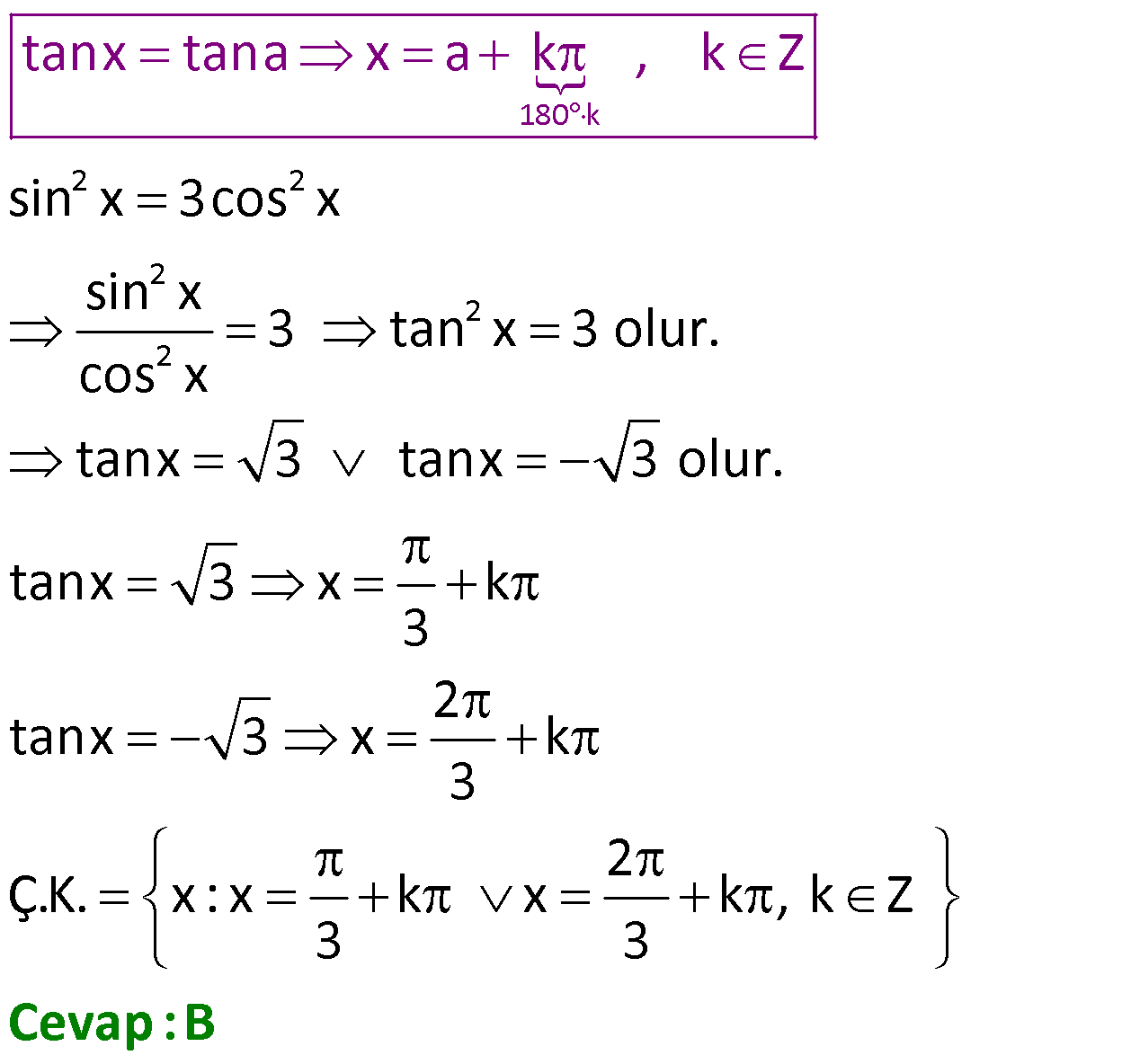
10.SORU
| | | | | |
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
TRİGONOMETRİK DENKLEMLER www.matematikkolay.net 1) 3 sin2x denkleminin çözüm kümesi aşağıda 2 kilerden hangisidir? A) x : x k x k , k Z 6 3 B) x : x 2k x 2k , k Z 6 3 2 C) x : x k x k , k Z 3 3 3 D) x : x 2k x 2k , k Z 3 3 E) x : x k x k , k Z 12 6 Çözüm: 360 k 360 2 .k 3 3 sin2x sin2x sin 2 3 2x 2k 2x 2k 3 3 x k x k olu sinx sina x a 2k x r a 2k (k Z) . 6 3 Cevap : A 2) sin 3x 10 sin 2x 50 denkleminin 0, 360 aralığında kaç kökü vardır? A) 4 B) 5 C) 6 D) 7 E) 8 Çözüm: sin 3x 10 sin 2x 50 3x 10 2x 50 360 .k 3x 2x 50 10 360 .k x 60 360 .k k 0 ise x 60 olur. 3x 10 180 2x 50 360 .k 3x 10 180 2x 50 360 .k 3x 10 130 2x 360 .k 3x 2x 130 10 360 .k 5x 140 36 0 .k x 28 72 .k k 0 x 28 k 1 x 100 k 2 x 172 k 3 x 244 k 4 x 336 Ç.K. 28 ,60 ,100 ,172 ,244 ,336 6 elemanlı Cevap : C 3) cos2x 1 sinx denkleminin 0, 2 aralığında çözüm kümesi aşağıdakilerden hangisidir? 7 11 7 A) 0, B) , C) 0, , 6 6 6 7 11 5 D) 0, , , E) 0, , , 6 6 6 6 Çözüm: TRİGONOMETRİK DENKLEMLER www.matematikkolay.net 2 cos2x 1 sinx (cos2x 1 2sin x yazalım.) 1 2 2sin x 1 2 6 sinx 0 sinx 2sin x sinx 1 2sinx 0 1 sinx 0 sinx 2 sinx 0 x 0 veya x 1 7 sinx sinx sin 2 6 7 7 x 2k x 2k 6 6 [0, 2 ) aralığındaki kökleri yazalım. 7 11 k 0 için x k 1 için x 6 6 Ç.K. 0, 7 11 , , 6 6 Cevap : D 4) cos 3x sin 2x denkleminin çözüm kümesi aşağıdakilerden hangisidir? A) x : x 18 72 .k x 90 360 .k, k Z B) x : x 90 360 .k x 180 360 .k, k Z C) x : x 90 360 .k x 270 360 .k, k Z D) x : x 18 360 .k x 270 360 .k, k Z E) x : x 18 72 .k x 270 360 .k, k Z Çözüm: 360 k 360 .k 90 360 c z cos 3x sin 2x ifadesinde sin 2x yerine cos 90 2x ya abiliriz. cos 3x cos 90 2x 3x 9 osx cosa x 2 a 2k x a 2k 0 2x 360 .k 3x 90 x 360 .k 5x 90 360 k 9 ( 6 k Z) x 0 3 0 .k x 18 360 .k x 270 360 .k Ç.K. x : x 18 72 .k x 270 360 .k, k Z Cevap : E 5) 2 2 2cos x sin x 2cosx 0 denkleminin 0, 2 aralığında kaç kökü vardır? A) 1 B) 2 C) 3 D) 4 E) 5 Çözüm: 2 2 2 2 2 2 2 3cosx 1 cosx 1 2cos x sin x 2cosx 0 ifadede sin x yerine 1 cos x yazalım. 2cos x 1 cos x 2cosx 0 3cos x 2cosx 1 0 3cosx 1 . cosx 1 0 1 cosx ve cosx 1 3 1 cosx değeri için I. ve IV. bölgede olmak üzere 3 toplam 2 kök vardır. cosx 1 x dir. Bir kök vardır. İfadenin toplam 3 kökü vardır. Cevap : C 6) sin7x sin3x.cos4x denkleminin 0,360 aral ığında kaç farklı kökü vardır? A) 16 B) 14 C) 12 D) 10 E) 8 Çözüm: TRİGONOMETRİK DENKLEMLER www.matematikkolay.net sin7x sin3x.cos4x ifadede sin7x yerine sin 4x 3x yazıp toplam formülü açılımı yapalım. sin 4x 3x sin3x.cos4x sin4x.cos3x sin3x.cos4x sin3x.cos4x sin4x.cos3x 0 sin4x 0 veya cos3x 0 dır. sin4x 0 4x 0 360 .k 4x 180 360 .k x 90 .k x 45 90 .k k 0 x 0 x 45 k 1 x 90 x 135 k 2 x 180 x 225 k 3 x 270 x 315 cos3x 0 3x 90 360 k 3x 90 360 .k x 30 120 .k x 30 120 .k k 0 x 30 x 30 k 1 x 150 x 90 k 2 x 270 x 210 k 3 x 390 x 330 90 ve 270 iki denklemden de ortak olarak geldi. Birer kez sayarsak; 12 kök bulunur. Cevap : C 7) cosx 3.sinx 2 0 denkleminin 0,360 aralığındaki çözüm kümesi aşağıdakilerden hangisidir? A) 75 ,165 B) 75 ,150 C) 65 ,165 D) 75 ,135 E) 135 ,225 Çözüm: 1 2 cosx 3.sinx 2 0 ifadesinde 3 yerine tan60 yazalım. cosx tan60 .sinx 2 sin60 cosx .sinx 2 cos60 cosx.cos60 sin60 .sinx 2 cos60 1 cos x 60 2. 2 2 cos x 60 cos x 60 cos135 2 x 60 135 360 .k x 60 135 360 .k x 75 360 .k x 195 360 .k k 0 x 75 k 1 x 165 Ç.K. 75 ,165 Cevap : A 8) 3 2.sin4x cos 2 3 4 Aşağıdakilerden hangisi yukardaki denklemin köklerinden biri değildir? 7 2 A) B) C) D) E) 12 6 2 12 3 Çözüm: TRİGONOMETRİK DENKLEMLER www.matematikkolay.net 3 2.sin4x cos 2 3 4 3 1 ifadede cos yerine yazalım. 4 2 1 2.sin4x 2 3 2 ifadeyi 2 ile genişletelim. 2. 2.sin4x 2 1 2 3 1 2. 3.1 2. 2 3 2.sin4x 1 4 2 3 2.sin4x 1 3 1 2 3 3 sin4x 4x 2k 4x 2k 2 3 3 x k x k. 12 2 6 2 k 0 x x 12 6 7 2 k 1 x x 12 3 7 2 Ç.K. , , , 12 6 12 3 Cevap : C 9) 2 2 sin x 3cos x denkleminin çözüm kümesi aşağıdakilerden hangisidir? 2 A) x : x 2k x 2k , k Z 3 3 2 B) x : x k x k , k Z 3 3 C) x : x k x k , k Z 6 6 D) x : x k x k , k Z 6 3 E) x : x 2k x 2k , k Z 6 3 Çözüm: 1 2 2 2 2 2 80 k t o sin x 3cos x sin x 3 tan x 3 olur. cos x tanx 3 tanx 3 lur. ta anx tana x a x nx 3 x k 3 2 tanx 3 x k 3 2 Ç.K. : x k x k , k Z Z 3 k k , 3 Cevap : B 10) tan x tan x 3 4 denklemini sağlayan en küçük pozitif açı için x sin Arctan değeri aşağıdakilerden hangisidir? 5 5 7 12 24 A) B) C) D) E) 12 13 25 13 25 Çözüm: tan x tan x 3 4 x 2x k 3 4 x x k 4 3 7 2x k 12 7 7 x k k 0 x 24 24 x 7 sin Arctan sin Arctan .24 7 Arctan olsun. 24 7 7 tan olur. sin bulunur. 24 25 Cevap : C
